基于灰色关联度和熵权法的公路网关键节点识别方法
王 元,郑贵省,王 鹏,张胜利
(1.军事交通学院研究生管理大队,天津300161;2.军事交通学院基础部,天津300161;3.军事交通学院学员旅,天津300161)
公路网络节点可被抽象为交叉口、公路交通枢纽和城镇,反映了不同粒度节点在网络中的作用,其中起重要枢纽作用的关键节点对路网结构安全、可靠性及路网整体性能发挥具有重要影响[1]。因此,路网中关键节点的识别对公路网的规划、管理,改造、增强公路网防灾抗毁性能,以及发展智能交通具有重要作用。
在公路网关键节点的识别研究中,国内外的学者都提出了公路网关键节点识别的评价指标和评价模型。从公路网关键节点的内涵出发,评价指标主要来源于反映公路网结构特性的相关指标以及公路网交通功能的相关指标。评价模型都是通过选择相应的评价指标来建立综合的评价体系。目前,许多学者通过对比总结提出了比较科学的路网关键节点的评价模型,但是现有的评价模型所形成的综合评价指标多具有主观性,并没有客观分析各项评价指标的贡献率,缺乏深入挖掘各项评价指标内在关系的方法[2]。本文借鉴灰色关联度和熵权法的相关理论和复杂网络关键节点的识别理论,改进现有的评价模型,以消除主观误差,提高识别结果的准确性。
1 公路网关键节点的评价指标
根据现有的公路网关键节点评价指标的研究成果,选择的评价指标有节点连接度、节点权值和节点流量。
1.1 节点的连接度
连接度ki反映了路网的局部特征,由与节点i相连的路段数决定,其值越大则对路网的影响越大,取值见表1。

表1 节点连接度取值
1.2 节点的权值
节点的权值由与节点相连的道路等级决定,计算公式为

式中:hi为节点i的权值;rij为与节点i相连的路段(i,j)的权值,rij取值见表 2。
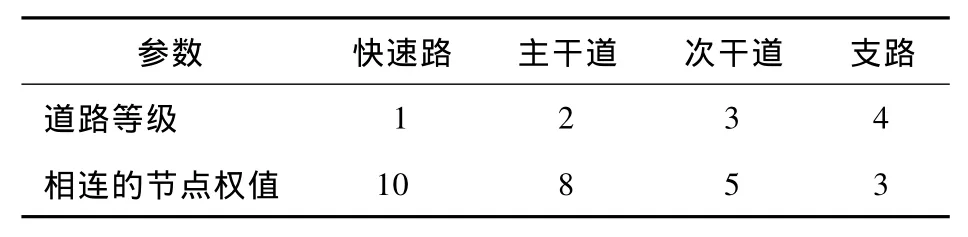
表2 不同等级路段的权值
1.3 节点流量
节点的流量wi为与其相连的各个路段的流量之和,计算公式为
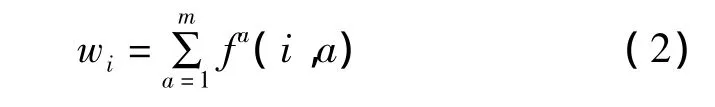
式中:m为与节点i相连的节点数;a为与节点i相连的第 a 个节点,a=1,2,…,m;fa(i,a)为与节点i相连的第a条路段上流量较大的车流方向的交通流量。
2 节点的重要度排序方法
熵是表示物质系统状态的一个物理量,表示该状态可能出现的程度,在信息论中,熵表示的是不确定性的量度。目标的信息熵越小,说明其指标的变异程度越大,提供的信息量也越大,而权重也越大。因此,可以根据熵值来确定每个指标的权重。
灰色关联是指事物之间的不确定关系,或系统因子之间、因子对主行为之间的不确定关系。灰关联分析是在灰色系统理论中分析离散序列间相关程度的一种测度方法[3],其基本原理是通过将比较序列和参考序列进行灰色关联计算,得到灰色关联度来评判相识程度[4]。在模型中,公路网节点的各项指标值越大则该节点的重要度越高,因此,选择所有目标节点中各指标的最大值作为参考序列。计算各节点的指标序列和参考序列的灰色关联度,灰色关联度越高,则节点越重要。
新的公路网关键节点的识别方法首先通过熵权法确定各评价指标的权重,再计算各节点的关联度来确定节点的重要程度,具体步骤如下。
(1)对n个节点、m个评价指标的初始矩阵

式中:i=1,2,…,n;j=1,2,…,m。
(2)归一化处理初始矩阵,得到矩阵B。

式中xmax、xmin为同一测度指标下的最大、最小值。
(3)计算指标j的熵Sj。

式中:K=1/ln n;Pij=,若 Pij=1,则 Pij=(1+bij)+bij))。
(4)计算指标j的熵权ωj。

式中;ri(j)为第i个节点的第j个指标的关联系数:ρ为分辨系数,取 ρ=0.5。
(8)计算关联度。
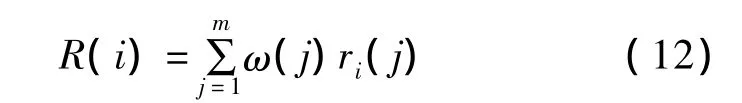
式中:ω(j)为第j个指标的权重;ri(j)为第i个节点的第j个指标的关联系数。
(9)比较各节点关联度的大小,得到各节点重要性排序。关联度越大,节点越重要。
3 原始数据无量纲化处理方法选择
将灰色关联度和熵权法应用到公路网关键节点的识别中,摆脱了评价过程中人为因素的影响。但存在原始数据无量纲化处理方法的选择问题。在实际应用中,可选数据无量纲化处理的方法很多,采用不同的方法会对处理结果产生较大的影响[5]。模型中式(8)为均值化的处理方法,实际中还需通过比较做出选择。
3.1 其他数据无量纲化处理的方法
(1)中心化处理。
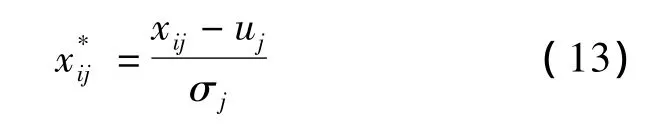
式中uj和σj分别为第j个指标下的样本均值和样本方差。
(2)极大化处理。
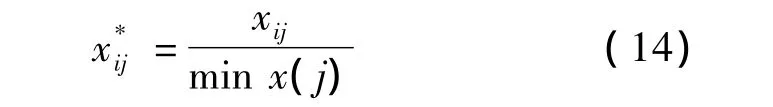
式中min x(j)为指标j下的最小值。
(3)极小化处理。

式中max x(j)为指标j下的最大值。
(4)极差化处理。

3.2 数据无量纲化方法选择的原则
在灰色关联度分析中,为保证达到最终节点重要性排序的目的,各节点之间的差异应该体现得越明显越好,因此应满足以下原则:
(1)Δ =max R(i)-min R(i),其中 i=1,2,…,n,且Δ尽可能大;
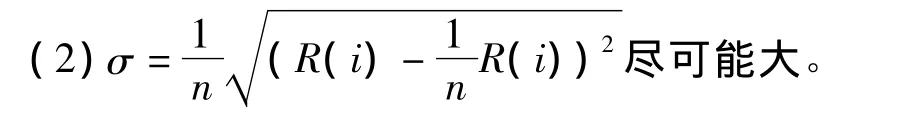
4 实例分析
4.1 实例数据
以10个北京市的路网节点的流量、连接度和权值数据为例(见表3)。
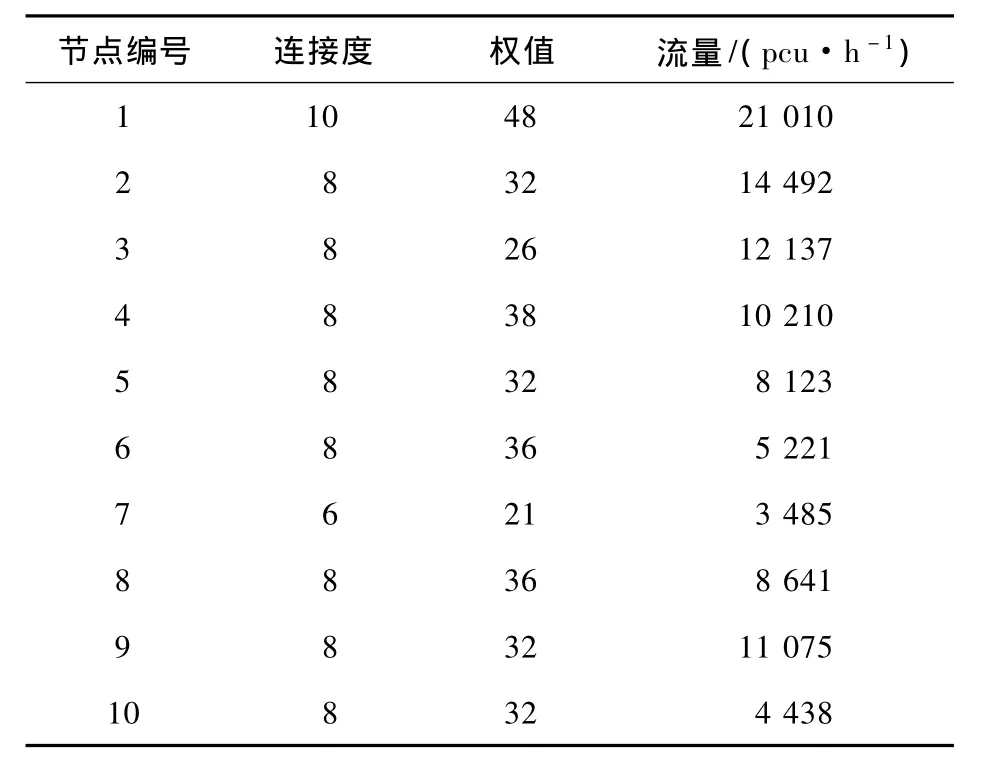
表3 节点的连接度、权值和流量
4.2 节点重要性排序结果
分别采用不同数据无量纲化处理的方法,采用Matlab编程计算得到灰色关联度、节点重要性排序及数据无量纲化方法的判断准则指标。按照连接度、权值和流量的顺序,权重计算结果为:w={0.281 1,0.298 5,0.420 4}。
分别采用不同的数据无量纲化处理方法所得到各节点的关联度见表4。节点排序结果及数据无量纲化方法选择原则的指标结果见表5。
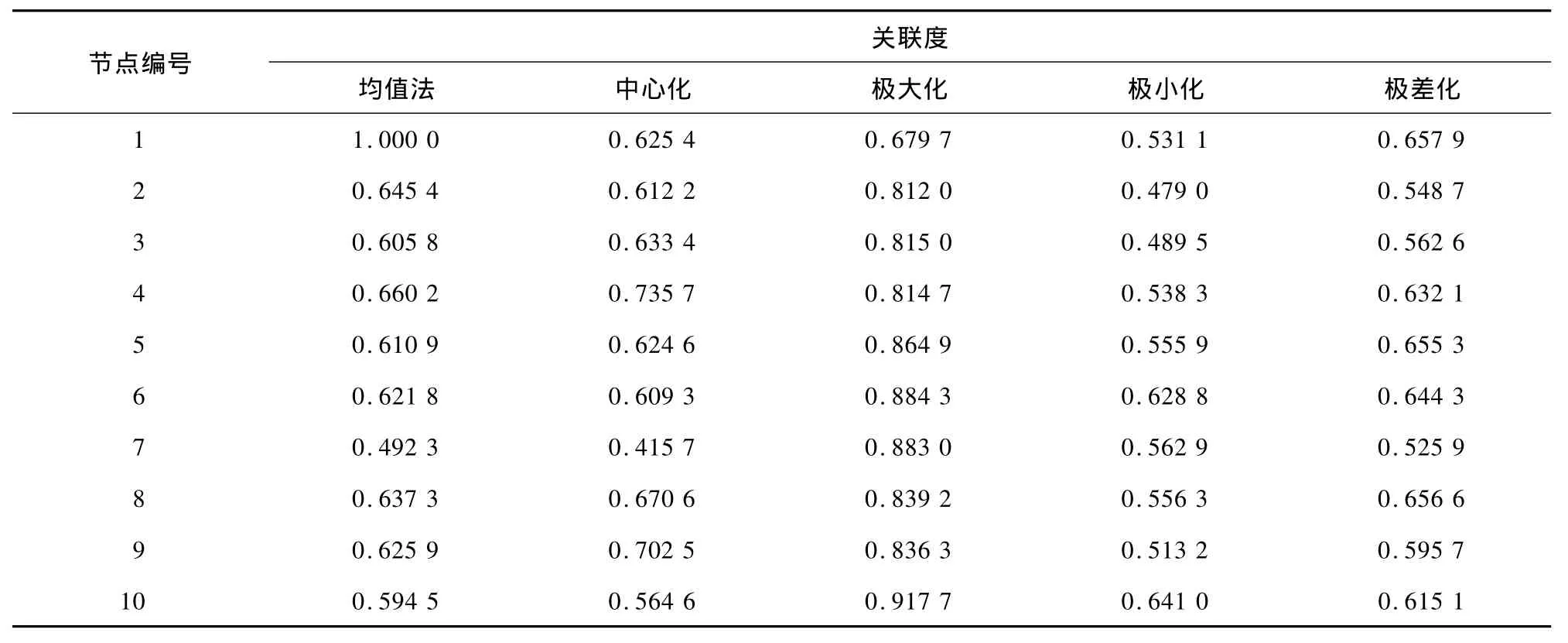
表4 关联度计算结果

表5 节点重要性排序结果
由表5可知,不同的数据无量纲化方法对排序结果有重要影响,根据数据无量纲化选择的原则,选择均值法作为原始数据处理的无量纲化方法,故提取出的10个北京市路网中的关键节点的排序结果为n1>n4>n2>n8>n9>n6>n5>n3>n10>n7。
5 结语
公路网的关键节点识别具有重要意义。在现有研究的基础上,将灰色关联度和熵权法的相关理论应用到公路网关键节点的评价模型中,改进了现有的评价模型。新的评价模型通过数学理论消除了综合评价过程中主观因素的影响,从而使路网中关键节点的识别过程更为科学合理。针对灰色关联度模型中不同的数据无量纲化处理方法对识别结果有较大影响,给出了解决的办法。通过实例分析,说明该评价方法在公路网关键节点识别中的可行性和有效性。
[1] 沈鸿飞,贾利民,王笑京,等.基于公路网结构特性的关键节点评价指标与辨识方法[J].公路交通科技,2012(9):138-139.
[2] 钟茹.路网中关键节点和重要路段的分析研究[D].北京:北京邮电大学,2013:15-18.
[3] 刘楠.农业产业结构调整与农业经济发展的灰色关联度分析:以黑龙江省为例[J].安徽农业科学,2010(14):7597-7598.
[4] 赵会茹,欧大昌,张奇,等.基于ANP灰色关联的电力用户重要性评估[J].能源技术经济,2012(24):39-40.
[5] 李炳军,朱春阳,周杰.原始数据无量纲化处理对灰色关联序的影响[J].河南农业大学学报,2002(36):199-200.

