LTE中抑制非视距误差的分层协同定位算法

后 茜，林基明，周继华，刘 俊

(1.桂林电子科技大学 信息科学实验中心，广西 桂林 541004；2.重庆金美通信有限责任公司，重庆 400030)

LTE中抑制非视距误差的分层协同定位算法

后 茜1，林基明1，周继华2，刘 俊2

(1.桂林电子科技大学 信息科学实验中心，广西 桂林 541004；2.重庆金美通信有限责任公司，重庆 400030)

针对长期演进技术(LTE)定位系统中非视距(NLOS)误差会使得用户终端测得的定位参数存在较大偏差，从而导致基于观测到达时间差(OTDOA)定位技术所估计的用户终端位置定位精度下降，以及传统Chan算法和Taylor级数展开算法中OTDOA协方差矩阵难以获取的问题，提出了一种抑制NLOS误差的分层协同定位算法(HCLA)。算法首先鉴别出含NLOS误差的基站，然后利用残差加权算法获取OTDOA协方差矩阵，再对传统的Chan算法和Taylor级数展开算法进行改进，将二者联合起来对用户终端进行分层协同定位。该算法无需知道OTDOA误差先验信息。仿真结果表明，NLOS环境下该算法能准确鉴别出含NLOS误差的基站，并能有效减小定位误差。

长期演进技术；定位；非视距误差；观测到达时间差；分层协同定位算法

随着移动通信技术的发展，基于位置的服务应用层出不穷，如救援定位、交通信息等，为了满足用户对这些业务的需求，移动终端的准确定位变得越来越重要。无线定位服务是LTE中一种应用前景最广的移动增值业务，故对LTE用户终端定位技术进行研究具有重要的应用价值。

LTE定位协议[1]中定义了3种定位方法：辅助全球导航卫星系统(Assisted Global Navigation Satellite System，A-GNSS)、增强型小区ID(Enhanced Cell ID，E-CID)和可观测到达时间差(Observed Time Difference of Arrival，OTDOA)。OTDOA是LTE系统中使用最多的定位技术，相比A-GNSS无需改动终端，且较E-CID定位精度高。LTE协议规定，OTDOA技术中利用服务基站到终端的距离作为参考距离，与其他基站的距离相减构成相应的双曲线模型实现终端定位。

Chan提出一种经典的OTDOA定位算法——Chan算法[2]，该算法在视距环境下定位精度高，计算复杂度低，但在非视距环境下，Chan算法定位精度将大大降低。为了消除NLOS误差的影响，Gentner C提出了基于粒子滤波器和卡尔曼滤波器的定位方法，能实现对动态用户的跟踪和定位，终端位置估计的均方根误差(RMSE)明显降低[3]。阎龙等提出一种适用于NLOS环境下的LTE终端迭代定位算法，算法无需信道先验信息，并可通过简单的分层细化来降低计算复杂度[4]。Yu K等提出了一种基于Taylor级数展开算法的二次线性规划算法来抑制NLOS误差的影响，但计算复杂度较高[5]。周康磊等提出利用残差值对定位结果进行加权以降低NLOS误差的影响，但计算复杂度高[6]。崔玮等提出利用高斯混合模型对含非视距误差的距离测量信息进行训练，并结合残差加权算法来降低NLOS误差的影响[7]。赵军辉等将点到点的距离转化为点到线的距离估计，但定位精度低[8]。Hara S等将摄动法引入终端定位算法中，在NLOS环境下可有效提高定位精度，但计算复杂度较高[9]。Kay S等基于最大似然估计算法提出一种新的最小加权二乘定位技术以消除NLOS误差带来的影响，但OTDOA先验信息难以估计[10]。在实际中，OTDOA误差先验信息未知，因此以上算法的应用存在局限性。为了解决这一问题，本文提出一种抑制非视距误差的LTE终端分层协同定位算法。首先对非视距误差进行鉴别，再根据残差加权法估计OTDOA值的先验信息，从而改进Chan算法和Taylor级数展开算法，将二者联合起来对LTE终端进行分层协同定位。在仿真中，将两种经典定位算法与其改进算法以及本文所提出的分层协同定位算法进行了对比。仿真结果表明，HCLA算法能有效鉴别出含非视距误差传播的基站，且其抑制非视距误差的能力强。

1 基于OTDOA的双曲线定位模型

设(x,y)为LTE终端坐标，(Xi,Yi)为第i个基站的已知位置，LTE终端到各基站距离为

(1)

式中：i=1,2,…,N，N为基站个数，则

(2)

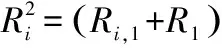
(3)

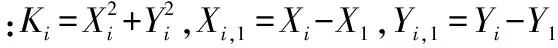
式(2)中由于NLOS误差的存在，使得含非视距误差的基站所在双曲线远离真实位置，形成一条新的双曲线，如图1所示。

图1 NLOS误差对LTE终端定位的影响

设基站3含NLOS误差，其余基站均为LOS传播，则由于非视距误差的影响，将基站3所在双曲线H3推移至H3′，使得双曲线H2与H3′形成交点A，以及H4与H3′形成交点B，均远离LTE终端真实位置。因此，有必要鉴别和抑制NLOS误差。

2 HCLA算法

2.1 非视距误差的鉴别

根据式(2)，OTDOA残差[6]定义为

(4)

NLOS传播鉴别步骤如下：

2) 每种基站组合分别计算出终端的估计位置作为其参考位置，利用式(4)计算OTDOA的残差，作为权值赋给组合内的每个基站；

3) 将每个基站从各个组合得到的权值相累加，得到各基站的总权值；

4) 对每个基站的总权值排序，总权值最大的基站即为含NLOS误差的基站。

2.2 非视距误差的抑制

2.2.1 残差加权算法

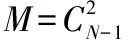
(5)

定义残差函数为

(6)

所有残差平方和为

(7)

对所有的(xk,yk)按下式加权得位置估计值

(8)

2.2.2 改进的Chan算法

在传统Chan算法中，OTDOA协方差矩阵通常假设为单位矩阵I，对非视距误差没有抑制作用，故在此提出将式(8)估计的初始值(xRW,yRW)代入式(6)得每个方程的残差，令

Q=diag{fi(xRW,yRW)},i=2,3，…,N

(9)

其中，Q为OTDOA协方差矩阵。

从式(3)中求得的具有OTDOA测量噪声的误差矢量为

(10)

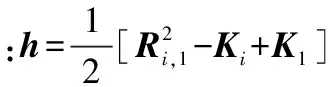
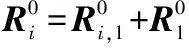
ψ=cBn+0.5c2n⊙n

(11)

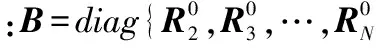
φ=E[ψψT]=c2BQB

(12)

式中：Q为OTDOA协方差矩阵。假设Za中的各元素相互独立，对Za进行第一次加权最小二乘(WLS)求解

(13)

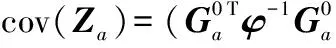
(14)

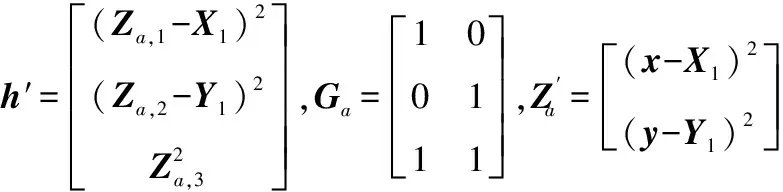
ψ′的协方差矩阵为

φ′=E[ψ′ψ′T]=4B′cov(Za)B′

(15)

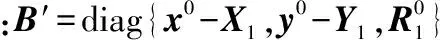
进行第二次WLS估计

(16)

最终LTE终端的定位计算结果为

(17)

2.2.3 改进的Taylor级数展开算法

传统的Taylor级数展开算法中，由于Q未知，可采用类似式(9)的方法来构造Q矩阵。

将式(2)进行泰勒级数展开，可得误差矢量

ψ=ht-Gtδ

(18)

采用WLS算法对式(18)求解得

(19)

(20)

此时的(x,y)即为LTE终端位置估计值。

Taylor级数展开后是否收敛取决于初始值(x0,y0)，可将改进的Chan算法估计的结果(xc,yc)作为其初始值展开，这样便得到改进的Taylor级数展开算法。

2.2.4 分层协同定位算法

为了更好地抑制非视距误差，将改进的Chan算法和Taylor级数展开算法联合起来进行分层协同定位，其流程如图2所示。

首先利用残差分析判决法对含NLOS误差的基站进行鉴别，然后采用残差加权法估计Q矩阵和位置初值，将Q矩阵和初值代入改进的Chan算法进行位置粗估计，更新Q值，再将粗估计值和更新的Q矩阵作为初始值代入Taylor级数展开算法中进行展开，得OTDOA测量误差的局部LS解，改进估计位置，然后继续代入改进的Chan算法进行位置估计，并更新Q矩阵，进行第i次Taylor迭代，直到OTDOA测量误差的局部LS解满足其设定的门限ε。

图2 HCLA算法流程图

3 算法仿真及分析

为了检验HCLA算法的实际定位性能，本文将HCLA算法和几种典型的定位算法在不同非视距误差、不同信道环境[11](远郊，郊区，一般市区B，一般市区A，闹市区)下进行仿真对比。假设LTE网络拓扑为经典的7基站，正六边形蜂窝网结构，小区半径为3 km，收敛门限为1 m，OTDOA测量误差服从均值为零，标准差为30 m的理想高斯分布，非视距误差分别为确定值(大小为视距传播距离的0～10%)和服从COST259信道模型两种情况。其中一个基站(非服务基站)含非视距误差，且所有基站均不提供OTDOA测量值先验信息。参与比较的算法为Chan算法、Taylor级数展开算法和残差加权算法，改进的Chan算法，改进的Taylor级数展开算法以及HCLA算法，用均方根误差(RMSE)和误差累计分布(CDF)表示定位精度，以上几种定位算法在NLOS误差传播环境下进行3 000次Monte-Carlo仿真。

非视距误差鉴别的仿真结果如图3所示。

图3 基站3含非视距误差

从图3中可以清晰看出，基站3的总加权值最大，故判定基站3含NLOS误差，与初始设定相符。

其次对各算法的定位性能进行仿真对比，实验结果如图4和图5所示。

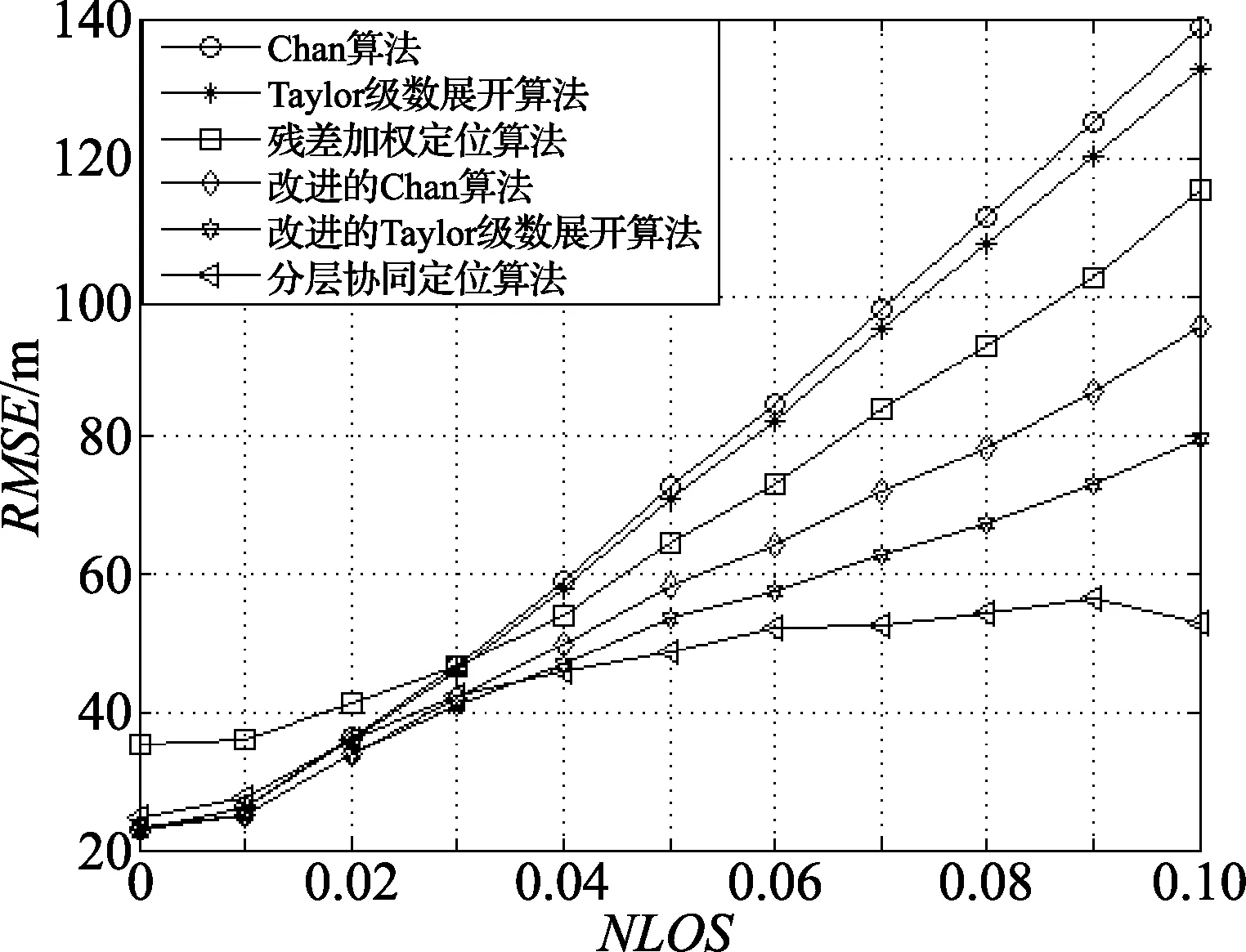
图4 各定位算法性能比较(RMSE)

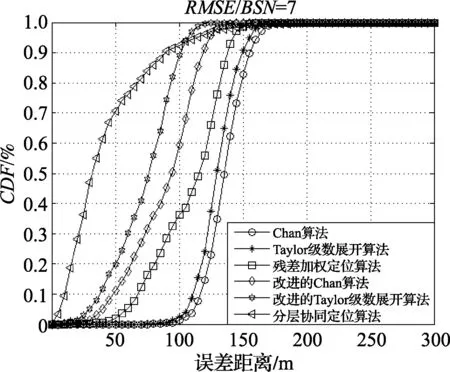
图5 各定位算法性能比较(CDF)

由图4可知，当NLOS误差超过一定程度，HCLA算法的均方根误差最小，且非视距误差越大，越能有效地抑制非视距误差对LTE节点定位精度的影响。由图5可知，HCLA算法在70%的概率下定位精度为50 m左右，在95%的概率下定位精度为100 m左右，优于其他典型定位算法的定位精度。

最后对各个定位算法在不同信道环境下的定位性能进行仿真对比，如图6所示。

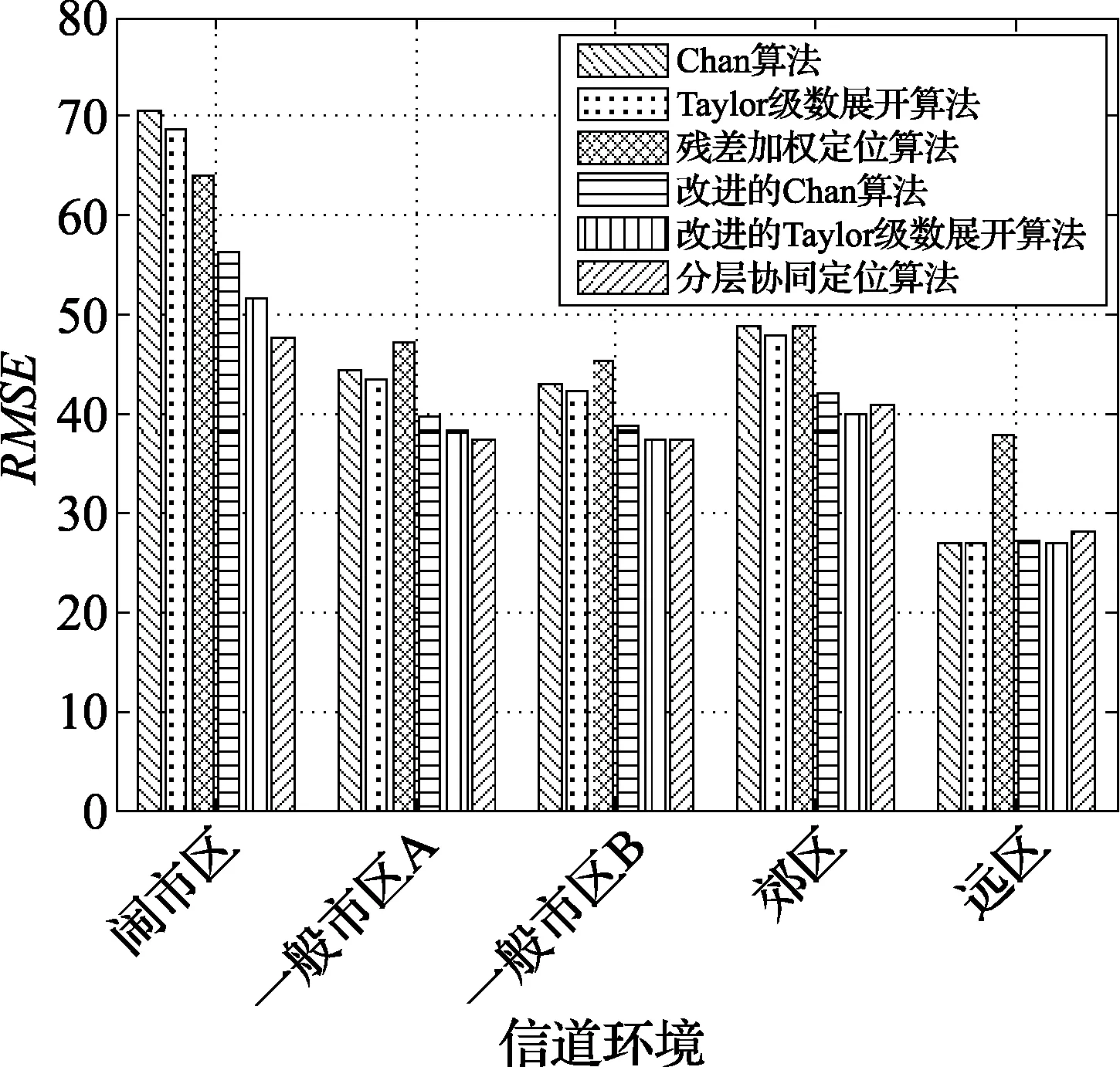
图6 不同信道环境下性能比较(RMSE)

从图6可以看出，随信道环境的恶化，HCLA算法抑制NLOS误差的能力变得显著，特别是在闹市区环境下。可见，HCLA算法在恶劣的信道环境下抑制NLOS误差的能力较强。

根据实验结果，算法的定位精度和迭代次数对比结果分别如表1和表2所示。

表1 算法定位精度对比 %

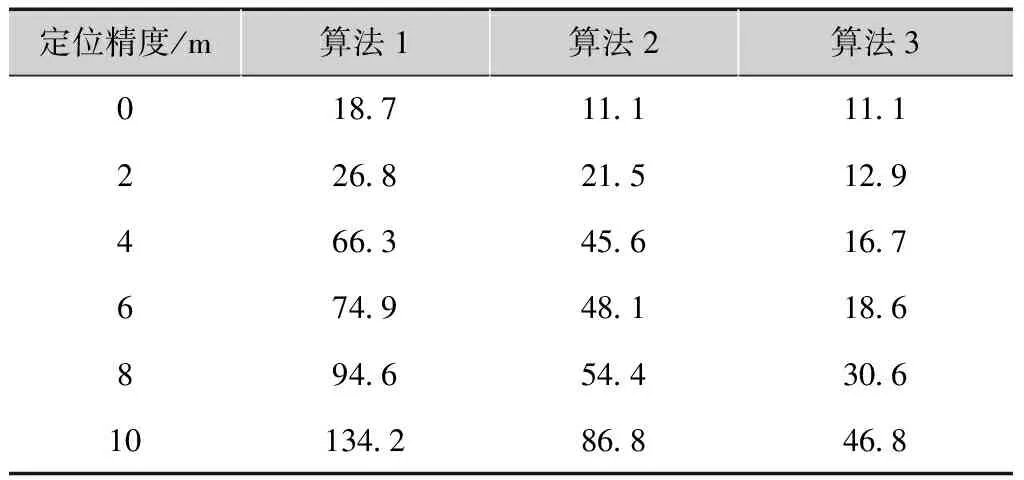
定位精度/m算法1算法2算法301871111112268215129466345616767494811868946544306101342868468

注：算法1为Taylor算法，算法2为改进的Taylor算法，算法3为HCLA算法。

表2 算法迭代次数对比 %

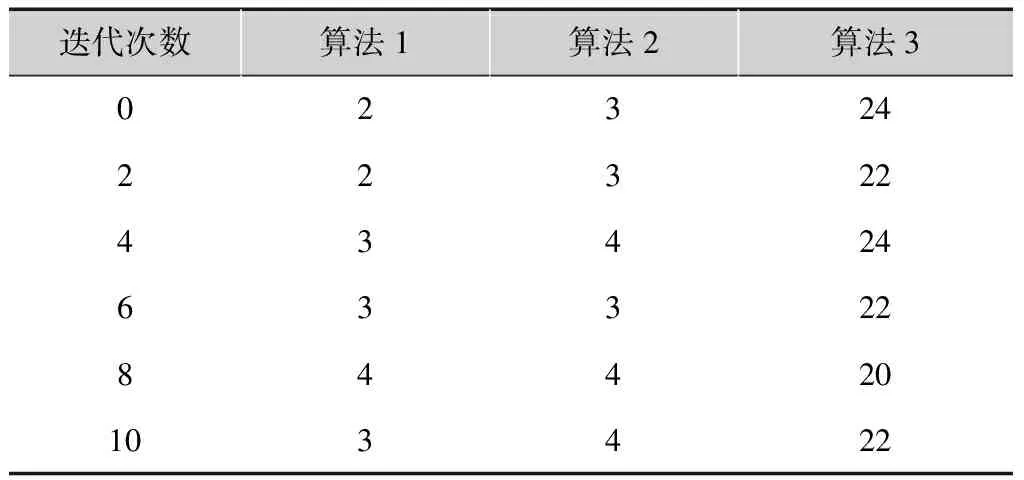
迭代次数算法1算法2算法30232422322434246332284420103422

注：算法1为Taylor算法，算法2为改进的Taylor算法，算法3为HCLA算法。

由表1、2可知，HCLA算法达到门限值时所需迭代次数较大，故与其他几种定位算法相比，计算复杂度较高，但其可以提高LTE终端的定位精度，因此综合考虑计算复杂度与定位精度间的关系，本改进算法具有更好的性能。

4 小结

本文对非视距误差的鉴别算法进行了改进，同时提出了一种无需OTDOA误差先验信息的分层协同定位算法(HCLA)，先鉴别出含NLOS误差的基站，再基于改进的Chan算法和Taylor级数展开算法对LTE终端位置进行分层协同定位。经过仿真分析，本算法能准确鉴别出含非视距误差的基站，且HCLA算法与几种典型的定位算法在同等条件下相比，对NLOS误差的抑制能力更强，定位精度更高，具有实际的应用价值。

[1] 3GPP TS 36.355 v9.0.0，3rd generation partnership project; technical specification group radio access network; E-UTRA; LTE positioning protocol[S]. 2009.

[2] CHAN Y T, HO K C. A simple and efficient estimator for hyperbolic location[J]. IEEE Trans. Signal Processing，1994，42(8)：1905-1915.

[3] GENTNER C, MUNOZ E, KHIDER M, et al. Particle filter based positioning with 3GPP-LTE in indoor environments[C]//Proc. Position Location and Navigation Symposium (PLANS). Myrtle Beach，SC：IEEE Press，2012：301-308.

[4] 阎龙，高泽华，高峰，等. 一种适用于NLOS环境的LTE终端迭代定位算法[J]. 计算机应用研究，2014，31(3)：876 -878.

[5] YU K，GUO Y J. Improved positioning algorithms for non-line-of-sight environments[J]. IEEE Trans. Vehicular Technology，2008，57(4)：2342-2353.

[6] 周康磊，毛永毅.基于残差加权的Taylor级数展开TDOA无线定位算法[J]. 西安邮电学院学报，2010(3)：10-13.

[7] 崔玮，吴成东，张云洲，等.基于高斯混合模型的非视距定位算法[J]. 通信学报，2014(1)：99-106.

[8] 赵军辉, 张雪雪, 曾龙基.提高NLOS环境下室内定位精度的新方法[J]. 北京邮电大学学报，2012(6)：38-43.

[9] HARA S，ANZAI D，YABU T，et al. A perturbation analysis on the performance of TOA and TDOA localization in mixed LOS/NLOS environments[J]. IEEE Trans. Communications，2013，61(2)：679-689.

[10] KAY S, VANKAYALAPATI N. Improvement of TDOA position fixing using the likelihood curvature[J]. IEEE Trans. Signal Processing，2013，61(8)：1910-1914.

[11] GREENSTEIN L J, ERCEG V, YEH Y S, et.al. A new path-gain/delay-spread propagation model for digital cellular channels[J]. IEEE Trans. Vehicular Technology，1997，46(2)：477-484.

后 茜(1988— )，女，硕士生，主研无线通信技术；

林基明(1970— )，教授，博士生导师，主要研究方向为无线通信技术；

周继华(1979— )，正高级工程师，主要研究方向为移动通信技术；

刘 俊(1971— )，工程师，主要研究方向为移动通信技术。

责任编辑：许 盈

Hierarchical Collaborative Localization Algorithm for Non-line-of-sight Error Mitigation in LTE

HOU Qian1，LIN Jiming1，ZHOU Jihua2, LIU Jun2

(1.GuangxiExperimentCenterofInformationScience,GuilinUniversityofElectronicTechnology,GuangxiGuilin541004,China； 2.ChongqingJinmeiCommunicationCo.,Ltd.,Chongqing400030,China)

In LTE (long term evolution) system, NLOS (non-line of sight) error can lead to a large deviation of the position parameters measured by UE (user equipment), resulting in a decrease of the position accuracy of estimated UE based on the OTDOA (observed time difference of arrival) positioning technology. OTDOA covariance matrix is difficult to be obtained in the traditional Chan algorithm and Taylor series expansion localization algorithm. To solve this problem, a hierarchical collaborative localization algorithm (HCLA), which can mitigate the NLOS error, is proposed in this paper. Firstly, the eNodeB that includes NLOS error is identified, then the OTDOA covariance matrix is obtained using the residual weighting algorithm, and then the Chan algorithm and Taylor series expansion algorithm are improved, finally, the two methods are combined to make hierarchical collaborative localization of UE. This algorithm can run without the priori information of OTDOA error. Simulation results show that, in NLOS environment, the eNodeB that contains NLOS error can be accurately identified, and the position error can be effectively reduced.

LTE; position; NLOS error; OTDOA; hierarchical collaborative localization

国家自然科学基金项目(NSFC61172054；NSFC61362006)；广西自然科学基金项目(2014GXNSFAA118387；2013GXNSFAA019334)；桂林电子科技大学研究生创新项目(GDYCS201409)

TN929.5

A

10.16280/j.videoe.2015.17.017

2015-04-20

【本文献信息】后茜，林基明，周继华，等.LTE中抑制非视距误差的分层协同定位算法[J].电视技术,2015，39(17).