无人机地形预处理低空突防轨迹规划技术*
翁兴伟,董康生,陈诚,程华
(1.空军工程大学 航空航天工程学院,陕西 西安 710038; 2.中国人民解放军95948部队,甘肃 兰州 732750)
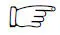
无人机地形预处理低空突防轨迹规划技术*
翁兴伟1,董康生1,陈诚2,程华1
(1.空军工程大学 航空航天工程学院,陕西 西安 710038; 2.中国人民解放军95948部队,甘肃 兰州 732750)
针对无人机低空突防飞行问题,提出了一种基于飞行器最大过载约束、爬升角约束和速度约束的数字地形直接平滑技术,设计了多步判断逻辑和山峰保护逻辑以提高平滑收敛速度和对山峰的保护,生成满足无人机飞行性能约束的安全可飞行曲面;在此曲面上进行轨迹规划,避免了复杂的轨迹可飞性和安全性处理工作,提高了轨迹规划效率;利用正交配点法将无人机轨迹规划问题进行离散化,转化为非线性规划问题,并利用序列二次规划方法进行攻击轨迹求解。仿真表明,该技术能快速生成可飞行的攻击轨迹。
地形预处理;无人机;安全可飞行曲面;正交配点法;轨迹规划
0 引言
察打一体中小型无人机具有长时间侦察、发现即打击等能力和优势,受到众多军事强国的青睐。它同时也具有低速、低空飞行的特点,因而在完成隐秘接敌和突防任务时,应选择低空飞行的方式[1]。低空飞行/突防难度与地形变化程度关系很大,且察打一体型无人机机动性能较差,在地形起伏变化较大的环境中很容易发生撞地事件[2-3]。为此,通过对地形进行预处理使得处理后的地形满足无人机飞行性能要求,即生成安全可飞行曲面,然后在该曲面上进行轨迹规划,生成的轨迹既能满足安全性要求又省略了轨迹可飞行的处理工作[2,4]。针对平滑算法易出现高程点相互拉高和不收敛缺点,本文通过设计多步判断逻辑和山峰保护逻辑对其进行了改进。
利用正交配点法对轨迹规划问题进行离散化处理,将轨迹规划问题转化为非线性规划问题(NLP),再利用序列二次规划方法进行求解,快速生成满足安全性、可飞性要求的攻击轨迹。
1 数字高程模型简介
目前,采用由美国太空总署(NASA)和国防部国家测绘局(NIMA)联合测量的SRTM数据,SRTM的全称为Shuttle Radar Topography Mission,即航天飞机雷达地形测绘使命。SRTM系统获得面积超过1.19亿km2的9.8万亿字节的雷达影像数据,雷达影像数据经过2年多的处理,制成了数字地形高程模型,该测量数据覆盖全球陆地表面的80%以上。
本文采用的数字地图编号为N33E069,地形如图1所示。

图1 数字高程模型地形Fig.1 Terrain of digital elevation model
2 数字地形直接平滑技术
无人机的飞行会受到机动性能的影响,这些性能主要包括最大爬升角、最大转弯半径、最大机动过载、飞行速度和飞行高度限制等[5-6]。安全可飞行曲面的生成就是通过这些约束对真实地形的坡度和曲率进行平滑处理,使得平滑处理后的地形能满足无人机的飞行性能要求。
2.1 数字地形坡度约束的处理技术
在低空突防中,无人机有最大航迹爬升角的限制。如果前方有一个坡度超过其最大航迹爬升角的山峰或障碍物,无人机就需要进行提前爬升,否则会导致机体与山峰或障碍物的碰撞。为了便于无人机的飞行和航迹的规划,对坡度大于最大可飞坡度的地形进行处理,使其满足无人机纵向飞行约束。
地形的坡度约束由无人机最大爬升角决定,因而无人机最大爬升角就是地形的最大坡度。地形坡度约束处理如图2所示。
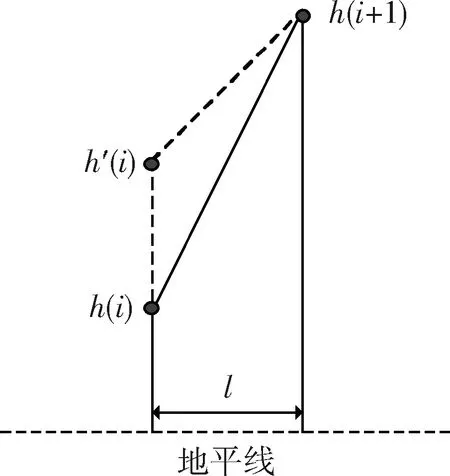
图2 地形坡度约束处理Fig.2 Terrain gradient process
图2中,i为网格点,h(i)为对应的高程值,l为网格间距。
记最大可飞坡度为
kmax,k=(h(i+1)-h(i+1))/l.
处理逻辑:
ifk>kmax,h(i)=h(i+1)-l·kmax,
(i=1,…,n)
else ifk<-kmax,h(i+1)=h(i)-l·kmax。
elseh(i)=h(i),h(i+1)=h(i+1)。
上述逻辑只考虑了相邻2个点之间的坡度问题,没有考虑坡度的整体变化趋势,需要多次迭代才能得到理想的效果,甚至可能会出现峰点相互拉高而不收敛的现象。
为提高坡度约束处理的效率,本文对上述逻辑进行了以下改进,具体步骤如下:
(1) 以最高山峰点为起点,依次对其两侧地形坡度进行处理。首先寻找每行、每列的最高山峰,并标记它们的位置;然后从最高山峰开始分别从正向和负向2个方向进行坡度约束处理;
(2) 对山峰进行保护。如果出现k<-kmax,采用如下逻辑:
while (h(i,j)-h(i,j+1))<=-l·kmax;
j=j+1;
c=c+1;
end
fork=1∶1∶c
h(i,j-k)=h(i,j-k+1)-l·kmax;
end
(3) 重复上述操作,直到满足精度要求。
采用上述改进逻辑,有以下好处:
(1) 大大提高了坡度约束的处理速度;
(2) 山峰不会被削平,得到了有效保护;
(3) 不会出现相互拔高的现象,能有效收敛,一般迭代1~2次就会收敛。
该方法的处理原理如图3所示。
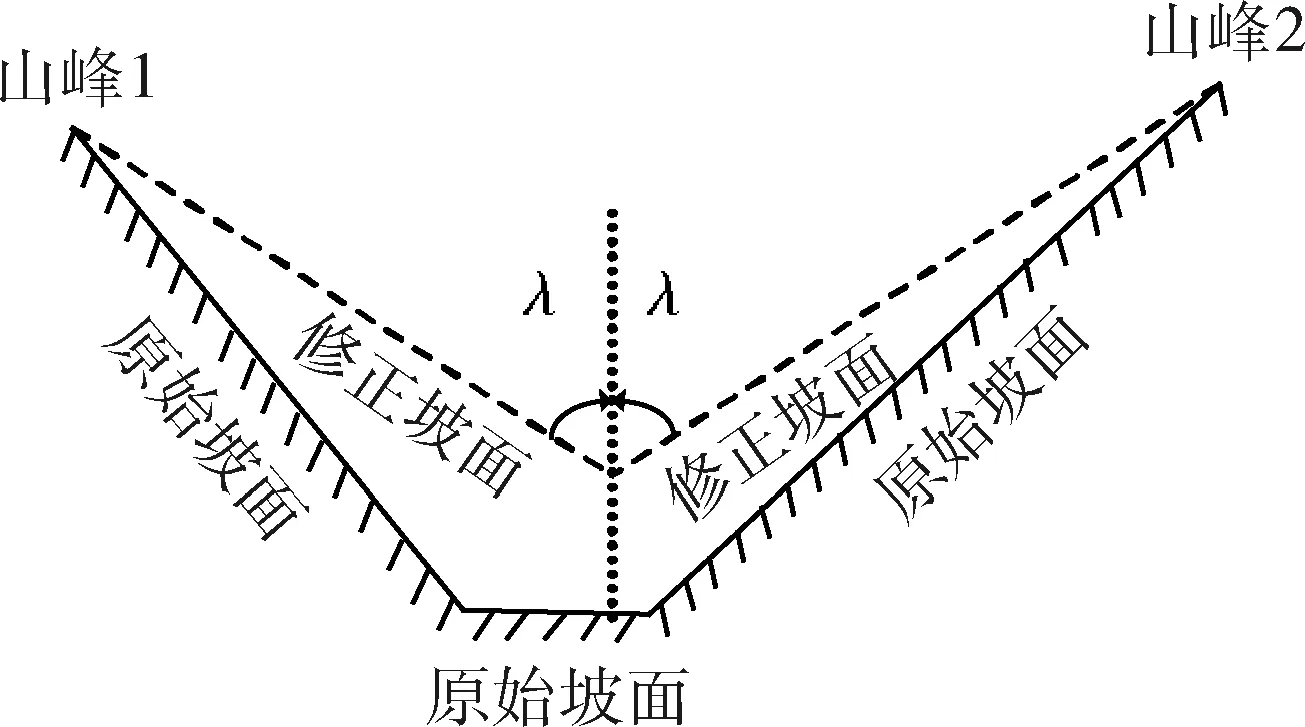
图3 改进的地形坡度约束处理Fig.3 Improved terrain gradient process
2.2 数字地形曲率约束的处理技术
无人机在铅垂平面内运动轨迹的曲率k和法向加速度nz的关系为
(1)
根据无人机的速度和最大法向加速度计算出地形曲率的最大值ρmax,然后对地形的曲率ρx,ρy进行约束处理,使它们的绝对值小于ρmax。
设地形高程函数为h=h(x,y),则曲率ρx为
(2)
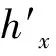

图4 地形曲率约束处理Fig.4 Terrain curvature process
曲率约束处理采用与坡度约束处理同样的逻辑,具体步骤如下:
(1) 在坡度约束处理完成的基础上,从最高山峰点两侧分别开始进行曲率约束处理;
(2) 网格点(xi,yj)的一阶偏导数为
(3)
网格点(xi,yj)处的二阶右偏导数为
h″x=(2hi-1,j-5hi,j+4hi+1,jhi+2,j)/l2.
(4)
网络点(xi,yj)处的二阶左偏导数为
h″x=(-hi-2,j+4hi-1,j-5hi,j+2hi+1,j)/l2.
(5)
将式(3)~(5)代入式(2)中,即可得到地形曲率ρx。
(3) 网格曲率约束的处理会改变原来已进行过坡度修正的地形,因而每次计算网格曲率之前都要进行网格坡度的重新判断和调整;
(4) 措施(3)已确保了地形坡度约束是满足的,因而山峰和山谷之间的网格点是不需要进行曲率修正的,曲率的约束处理只存在于山峰和山谷。为了对山峰进行保护,山峰和山谷的处理方法是不一样的。具体逻辑如下:
记Δh=1/5·l2(ρ-ρmax)(1+h′2)(3/2),
ifρ<-ρmax,thenh(i-1,j)=h(i,j)-Δh,
h(i+1,j)=h(i,j)-Δh;
ifρ>ρmax,thenh(i,j)=h(i,j)+Δh。
2.3 安全离地高度
为确保无人机尽可能的贴近地面飞行且又能有效避免与地面相撞,需要给无人机设定一个安全的离地高度。不同地形的无人机安全离地高度是不一样的,一般认为低空突防的最佳离地高度:海面为15~30 m,陆地平原地区为60~80 m,丘陵山区为120 m左右。
2.4 地形平滑效果分析
仿真条件:最大爬升角β=10°,最大过载nz=4,飞行速度v=200 m/s,地形网格点间距100 m。
仿真结果如图5~8所示。

图5 坡度约束处理后地形图Fig.5 Terrain processed through gradient

图6 曲率约束处理后的数字地形Fig.6 Terrain processed through curvature

图7 平滑后地形与原地形之差Fig.7 Errors of processed terrain to the original

图8 平滑地形与原地形比较Fig.8 Comparison of processed terrain and the original
从仿真结果看,曲率约束处理的地形平滑效果非常显著,且对地形高程的改变在400 m以内,对原始地形、地貌的改变很小。同样,曲率约束处理有效保护了原始地形山峰,这对无人机安全飞行是有益的。
2.5 安全可飞行曲面生成
在直接平滑法得到的可飞行曲面加上地形的特征安全高度就可得到无人机安全可飞行曲面。论文采用的地形为丘陵山区,无人机安全离地高度取为200 m,得到安全可飞行曲面如图9所示。
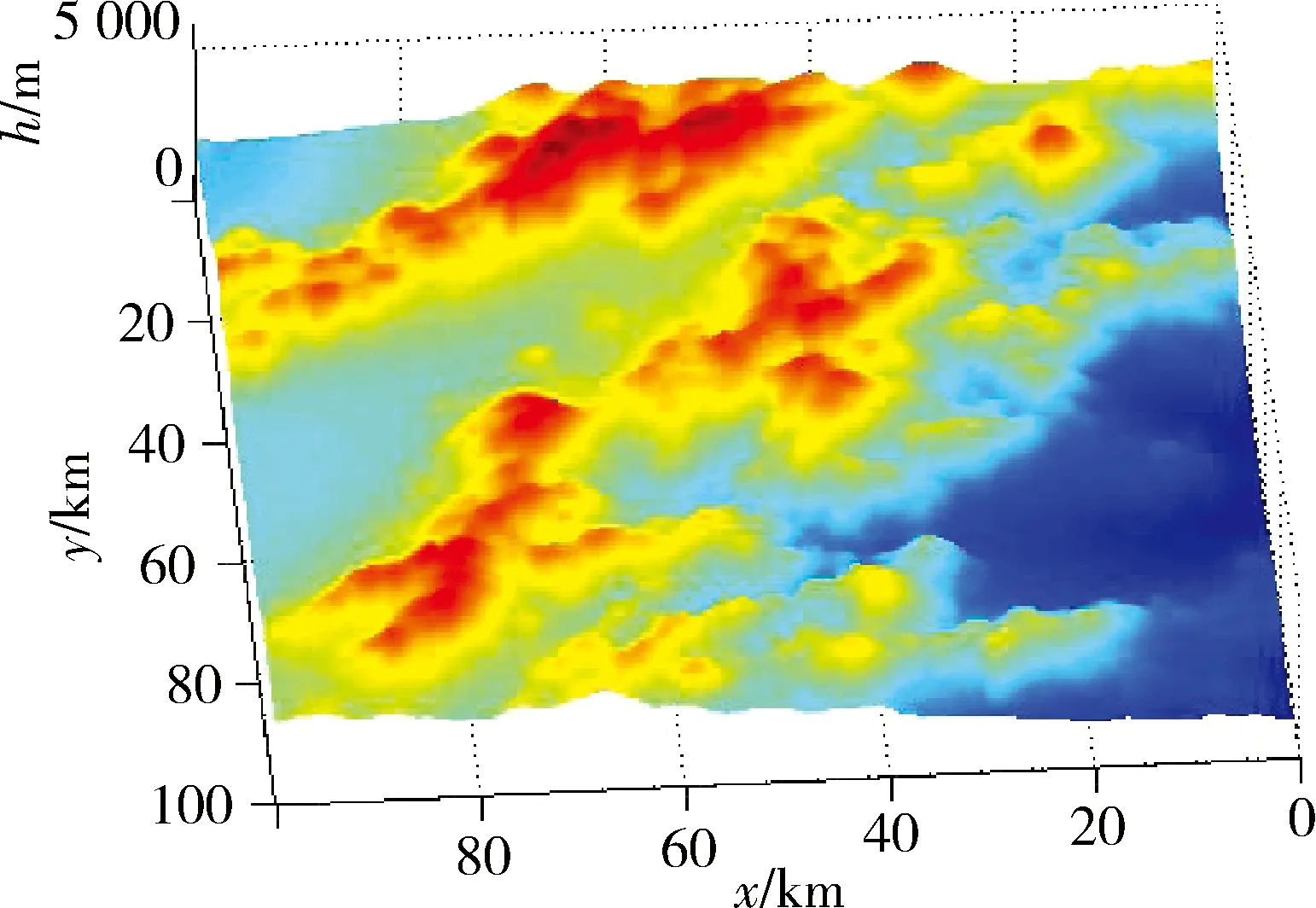
图9 安全可飞行曲面Fig.9 Safe and flyable curve
3 基于正交配点法的轨迹快速规划
配点法具有对初值不敏感、可有效处理约束、适应性强等特点,成为了解最优化问题的重要方法,在高超声速飞行器最优弹道、卫星姿态调整等方面取得了很好效果[7-9]。配点法同时对控制量与状态量进行离散化,将轨迹最优化问题转化为NLP问题,然后在利用解NLP问题的方法进行最优轨迹的规划[10]。将Legendre多项式的根作为配置点,因Legendre多项式的根具有正交性,这种方法也被称为正交配点(orthogonal collocation)法[11]。Gauss伪普法作为一种正交配点法的最新发展成果,以其求解精度高、收敛速度快在复杂最优控制尤其是飞行器轨迹规划问题中得到广泛应用[10,12]。本文也采用此方法,具体方法如下:
(1) 时域转换
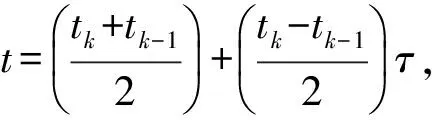
(6)
(2) 状态变量和控制变量的Lagrange全局插值逼近
Gauss伪谱法取N阶Legendre-Gauss(LG)配置点和τ0=-1初始点作为插值点,构成N+1个Lagrange插值多项式逼近状态变量,状态变量的插值多项式近似表示为
(7)

与状态变量不同的是,控制变量插值点只包含配置点,以K个Lagrange插值多项式来逼近控制变量,状态变量的插值多项式近似表示为
(8)
(3) 动力学微分方程转换为代数约束
(9)

(10)

从而将运动微分约束转换为代数约束:
(11)
(4) 终端状态估计
状态变量的多项式逼近表达式未包括终端时刻节点,终端状态应满足动力学方程约束,即
(12)
将终端约束条件离散并用Gauss积分来近似:
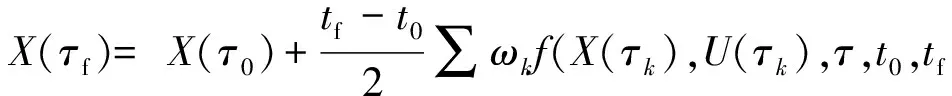
(13)
(5) 最优控制问题伪谱法的综合描述
经上述变换,将轨迹规划最优控制问题转化为具有一系列代数约束的参数优化问题,即非线性规划问题(NLP)。其标准形式为
(14)
轨迹求解算法流程如图10所示。

图10 轨迹求解算法流程Fig.10 Trajectory solving method flow
4 仿真与分析
将已探明雷达威胁和防空火力威胁加载到安全可飞行曲面上,得到综合威胁信息的安全可飞行曲面,如图11所示。

图11 综合威胁的安全可飞行曲面Fig.11 Safe and flyable curve composed threat
在综合威胁的安全可飞行曲面上进行轨迹规划仿真。仿真条件:采用文献[1]中的无人机模型,轨迹起点坐标为(0,0,2),终点坐标为(100,80,3)。规划结果如图12,13所示。
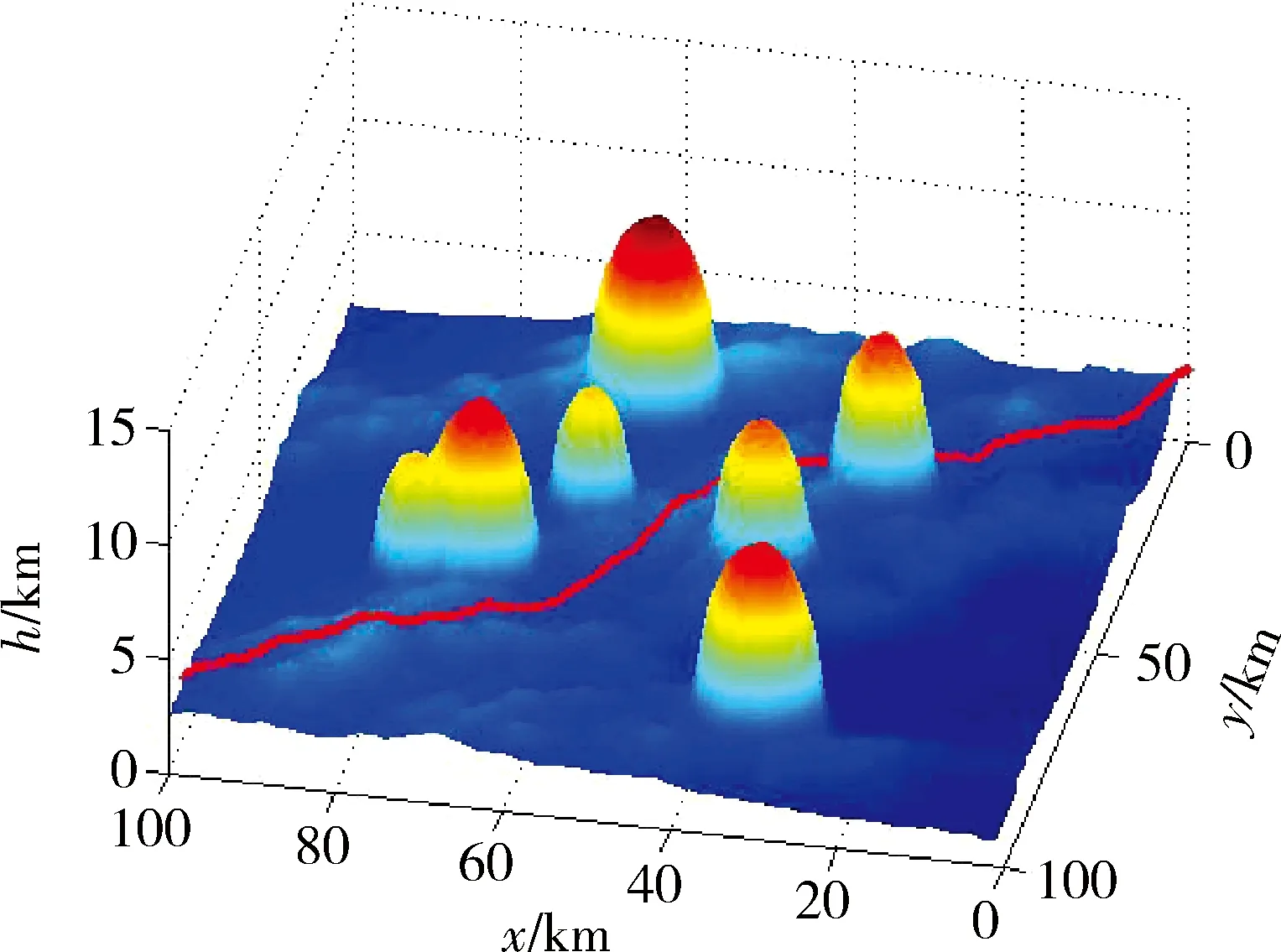
图12 攻击轨迹3D图Fig.12 Three dimensional diagram of attack trajectory
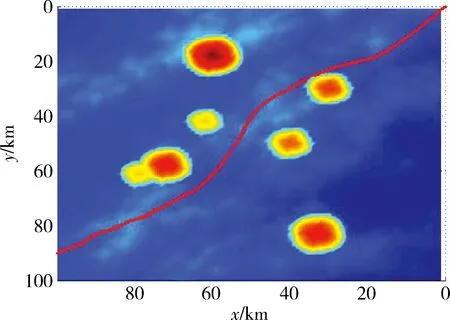
图13 攻击轨迹俯视图Fig.13 Top view of attack trajectory
仿真结果分析:轨迹规划仿真求解用时1.3 s得到收敛的最优轨迹,表明算法具有较好的实时性较强的收敛性。从轨迹规划结果图12,13可以看出,轨迹紧贴安全可飞行曲面,部分轨迹紧贴威胁源边界,表明该算法能在复杂环境下生成高精度的攻击轨迹。
5 结束语
中小型察打一体无人机具有低空、低速和弱机动的特性,规划的飞行规划具有很好的可飞行和安全性。低空突防作为其主要的飞行方式,如何在该环境下进行安全可靠的轨迹规划正是本文的研究内容。根据无人机最大爬升角、最大法向过载和飞行速度约束对数字地形坡度和曲率进行平滑处理,生成满足无人机飞行性能要求的可飞行曲面,再加上安全离地高度就得到安全可飞行曲面。本文提出的数字地形直接平滑处理技术,设计了山峰保护逻辑对山峰进行保护,并采用了多步判断逻辑使得地形平滑能快速有效收敛。利用正交配点法对轨迹规划问题进行离散化转化为NLP问题,并利用序列二次规划方法进行求解。仿真结果表明该方法具有复杂环境解算能力、精度高和收敛速度快等优点。
[1] 黄长强,曹林平,翁兴伟,等.无人作战飞机精确打击技术[M]北京: 国防工业出版社,2011:123-128. HUANG Chang-qiang, CAO Lin-ping, WENG Xing-wei, et al. Precision Strike Technology for UCAV[M]. Beijing: National Defense Industry Press,2011:123-128.
[2] 唐强,张新国,刘锡成. 一种用于低空飞行的在线航迹重规划方法[J]. 西北工业大学学报, 2005, 23(2):271-275. TANG Qiang, ZHANG Xin-guo, LIU Xi-cheng.Exploring an Online Method of Vehicle Route Re-Planningfor Low Altitude Flight[J]. Journal of North-western Polytechnical University,2005, 23(2):271-275.
[3] 白晓利, 韩亮. 基于数字地图预处理的低空突防飞行路线规划[J].北京航空航天大学学报, 2005, 31(8):853-857. BAI Xiao-li, HAN Liang.Path Planning for Penetrating Aircraft to Fly at Low Altitudesbased on Technology of Digital Elevation Map[J]. Journal of Beijing University of Aeronautics and Astronautics, 2005, 31(8):853-857.
[4] 陈侠, 鹿振宇. 基于不同地形的低空安全突防曲面处理算法[J]. 电光与控制,2013, 20(5):1-5. CHEN Xia, LU Zhen-yu. Processing Algorithm for Low-Altitude Penetration Safety Surface Based on Different Types of Terrain[J]. Electronics Optics & Control, 2013, 20(5): 1-5.
[5] 孙立军.基于突防网格模型的动态航迹规划[J]. 现代防御技术,2013,41(2):128-132. SUN Li-jun. Dynamic Programming Trajectory Planning Base on Penetration Gridding Model[J]. Modern Defence Technology,2013,41(2):128-132.
[6] 刘家宁. 直升机低空突防与地形跟随技术研究[D]. 南京:南京航空航天大学,2007. LIU Jia-ning.Research on Low Altitude Penetration and Terrain Following of Helicopter[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2007.
[7] WEI Kang,Naz Bedrossian. Pseudospectral Optimal Control Theory Makes Debut Flight, Saves NASA $1Min Under Three Hours[N]. SIAM News, 2007, 40(7).
[8] 雍恩米. 高超声速滑翔式再入飞行器轨迹优化与制导方法研究[D].长沙:国防科技大学,2008. YONG En-mi. Study on Trajectory Optimization and Guidance Approach for Hypersonic Glide-reentry Vehicle [D].Changsha: National University of Defense Technology, 2008.
[9] 宗群,田柘苓,窦立谦.基于Gauss伪谱法的临近空间飞行器上升段轨迹优化[J].字航学报,2010, 31(7):1775-1781. ZONG Qun, TIAN Bai-ling, DOU Li-qian. Ascent Phase Trajectory Optimization for Near Space Vehicle Based on Gauss Pseud0spectral Method[J]. Journal of Astronautics.2010, 31(7):1775-1781.
[10] 张煜,张万鹏,陈璟,等.基于Guass伪谱法的无人机对地武器投放轨迹规划[J].航空学报, 2011, 32(7): 1240-1251. ZHANG Yu, ZHANG Wan-peng, CHEN Jing. Air-to-Ground Weapon Delivery Trajectory Planning for UCAVs Using Gauss Pseudospectral Method[J].Acta Aeronauticaet Astronautica Scinica, 2011 ,32(7):1240-1251.
[11] BENSON A, THORVALDSEN T, RAO V. Direct Trajectory Optimization and Costate Estimation via an Orthogonal Collocation Method[J]. Journal of Guidance, Control and Dynamics, 2006, 29(6): 1435-1440.
[12] I Michael Ross, Mark Karpenko. A Review of Pseudospectral Optimal Control: From Theory to Flight[J]. Annual Reviews in Control, 2012, 36 :182-197.
Low Altitude Penetration Trajectory Planning for Unmanned Aerial Vehicle(UAV) Terrain Pre-processing
WENG Xing-wei1,DONG Kang-sheng1,CHEN Cheng2,CHENG Hua1
(1.AFEU,Aeronautics and Astronautics Engineering School,Shaanxi Xi’an 710038,China;2.PLA,No.95945 Troop,Gansu Lanzhou 732750,China)
Aiming to solve the problem of low altitude penetration for unmanned aerial vehicle (UAV), a digital terrain direct smooth method is proposed based on constraint of max overload, club angle and speed. Safe and flyable cure generated with this method can meet constrains of UAV flight performance. Complex process of flyability and safety is avoided by means of planning on this curve and thus the efficiency of trajectory planning is improved for UAV. The problem of UAV trajectory planning is discretized by using orthogonal collocation and is conversed into nonlinear programming problem (NLP), and then optimum trajectory is acquired by using sequential quadratic programming method to solve the transformed NLP. Simulation results show that the proposed method can quickly generate flyable attacking trajectory.
terrain pre-processing; unmanned aerial vehicle(UAV); safe and flyable cure ;orthogonal collocation;trajectory planning
2014-09-13;
2014-10-27
翁兴伟(1978-),男,黑龙江齐齐哈尔人。讲师,博士,研究方向为武器系统总统技术及无人机自主攻击技术。
通信地址:710038 陕西省西安市灞桥区霸陵路1号 E-mail:kgddks@163.com.
10.3969/j.issn.1009-086x.2015.04.004
V279
A
1009-086X(2015)-04-0019-06

