关于S-投射模

张永亮, 丁南庆(. 安康学院 数学与统计系, 陕西 安康 725000; 2. 南京大学 数学系, 江苏 南京 20093)



关于S-投射模

张永亮1, 丁南庆2*
(1. 安康学院 数学与统计系, 陕西 安康 725000; 2. 南京大学 数学系, 江苏 南京 210093)

设R为任意的幺环.Azumaya 将投射模的概念推广到S-投射模.文献(Zhu S L. J Algebra,1991,139:255-261.) 讨论了在什么样的环上，平坦模是f- 投射的.文献(Mao L X. Taiwanese J Math,2007(12):501-512.)给出了内射模都是S-投射的环.讨论S-投射模和其他模的关系，如投射模、平坦模、拟内射模、可除模、S-平坦模等，并证明了S-投射模关于直和的封闭性.

S-投射模; 平坦模;S-平坦模

1 引言及预备知识

M. F. Jones[1]给出了f-投射模的概念.G. Azumaya[2]对f-投射模和S-投射模进行了系统的研究.设f:A→C为满同态，如果Hom(M,f)仍然是满射，则称f是M-纯的.如果对于所有有限生成R-模M，f:A→C是M-纯的，则称f是f-可裂的.类似的，如果对于任意的循环模M，f是M-纯的，则称f为S-可裂的.如果任意的满射f:A→M是f-可裂(S-可裂)，则称模M为f-投射(S-投射)的.G. Azumaya证明了每个S-投射模的纯子模都是S-投射模；如果R是左诺特环或者交换整环，则每个平坦模都是f-投射模.如果R是整环，则每个平坦R-模都是S-投射模.S. L. Zhu[3]研究了每个平坦模都是f-投射模的环，证明了每个平坦左R-模都是n-投射的当且仅当每个平坦左Mn(R)-模都是S-投射模.

本文在前人研究的基础上，对S-投射模进行研究，给出了S-投射模与各种模的关系.设R为环，本文证明了每个拟内射右R-模都是S-投射模当且仅当R是半单环.由定义可知，每个f-投射模都是平坦模，但S-投射模并不一定是平坦模.本文证明了在R是交换整环的情况下，每个S-投射R-模都是平坦模当且仅当R是Prüfer整环.设R是交换环，S⊂R为乘性子集，且不含零因子，如果每个S-投射R-模都是平坦模，则每个S-投射S-1R-模都是平坦S-1R-模.并证明了每个平坦R-模都是S-投射模当且仅当任意f-投射R-模的直极限是S-投射模.如果R是自内射环，则R是QF-环当且仅当每个S-投射R-模是投射模.最后，证明了S-投射模的直和仍然是S-投射的.

本文中所用的定义和符号都是标准的.对于没有解释的概念和符号，请参见文献[4].

2 S-投射模与拟内射模

定义 2.1 设M为右R-模，如果任意满同态f:N→M和任意的同态g:C→M,其中C为循环R-模，存在h:C→N，使得g=fh，则称MR为S-投射模.

定义 2.2 设R为环，如果每个循环右R-模嵌入一个自由R-模，等价地，每个左理想I，都存在有限集合X⊂R，I=annl(X)，则称R为右CF-环.

从文献[2]中知道，环R是右CF-环当且仅当每个内射右R-模是S-投射的.那么，在什么情况下，所有的拟内射右R-模是S-投射的呢？有以下结论：

命题 2.1 对于一个环R,下列条件等价：

1)R是半单环；

2) 每个循环R-模是S-投射的；

3) 每个拟内射R-模是S-投射的；

4) 每个单R-模是S-投射的.

证明 1)⟹2)、1)⟹3)、1)⟹4)是显然的，因为半单环R上的任意R-模都是投射的，从而是S-投射的.

2)⟹4) 每一个单模必是循环模.

4)⟹1) 假设条件4)成立，只需证明每个单R-模是投射的.设MR是单R-模，由于MR的非零子模只有MR自身，MR是S-投射R-模意味着，MR是某一个自由R-模的直和项，从而是投射的.

3)⟹4) 每个单R-模都是拟内射的.

在文献[2]中，作者证明了下面的命题：

命题 2.2 如果AR是拟内射R-模，那么AR的每一个S-可裂子模都是AR的直和项.

实际上,可以将该结论推广到CS-模:

定义 2.3[4]设MR为R-模.如果N⊂cM蕴含N⊂⨁M，则称MR为CS-模.

命题 2.3 如果M是S-投射右R-模，A是CS右R-模，那么正合列0→B→A→M→0可裂.

证明 由文献[2]的命题3可知，B在A中是本质闭的，即B⊂cA，而A为CS-模，所以B⊂⨁A.

设M为右R-模，如果对于任意的a∈R，都有Ext1(R/Ra,M)=0，则称模M为可除的.如果RR是可除右R-模，则称环R为右可除的.

考虑另一个问题：在什么条件下所有的可除模都是S-投射的,称这样的环为DSP-环，得到以下的结论：

命题 2.4 一个环R是半单环当且仅当R是Neumann 正则环和DSP-环.

证明 “⟹” 显然.

“⟸”R是Neumann正则环当且仅当每个模是可除模.再由命题1.1知道，R是半单环.

命题 2.5 如果R是Dedekind-整环，那么R是CF-环当且仅当R是DSP-环.

证明 在Dedekind-整环上，所有的可除模都是内射模.而在CF-环上，所有内射模都是S-投射模.

引理 2.1[4]如果R是主右理想环，则MR是可除的当且仅当MR是内射模.

命题 2.6 如果R是一个主右理想环，则R是CF-环当且仅当R是DSP-环.

证明 在主右理想环上，所有的可除模都是内射模.而在CF-环上，所有内射模都是S-投射模.

作为凝聚环的一种推广，如果环R的每个主左理想都是有限表现的，则称R是左P-凝聚环.如果对于环R的任意非空子集X，annl(X)(annr(X))是有限生成的，则称R为左(右)AFG-环.如果R既是左AFG-环，又是右AFG-环，则称R是AFG-环.从文献[2]中可知，如果R是一个整环，那么右R-模MR是S-投射的当且仅当它是无挠的.结合文献[5]，有以下结论：

命题 2.7 如果R是整环，那么R是右P-凝聚环当且仅当它是AFG-环.

证明 由文献[6]的定理2.7知，R是P-凝聚当且仅当∏RR是无挠的，而R是整环，从而∏RR是S-投射模，从而R是AFG-环[5].

命题 2.8 如果环R是P-凝聚整环，那么R是右可除环当且仅当R是右CF-环.

证明 在P-凝聚的条件下，R是可除环当且仅当每个内射模M是无挠的，而R是整环，因此M是S-投射的，由文献[5]的引理3.6知，R是CF-环.

3 S-投射模和平坦模

通过定义，很容易知道，每个f-投射模都是平坦模.那么，是不是每个S-投射模都是平坦模呢？下面的结论给出了否定的答案：

命题 3.1 交换整环R是Prüfer整环当且仅当每个S-投射R-模是平坦的.

证明 这是文献[7]推论2.6的一个直接的推论.

命题 3.2 对于环R,下列条件等价：

1) 任何平坦右R-模都是S-投射的.

2) 设0→A→B→C→0是纯正合列，其中B是f-投射右R-模，则C是S-投射的.

3)f-投射右R-模的任意直极限是S-投射的.

证明 1)⟹2) 由于B是f-投射的，则必是平坦右R-模，从而0→A→B→C→0是纯正合的当且仅当C是平坦的.再由1)知，C是S-投射的.

引理 3.1[9]设R为交换环，S⊂R为乘性子集.如果M是平坦R-模，则S-1M是平坦S-1R-模.

引理 3.2[10]设R为交换环，S⊂R为乘性子集.对于任意的S-投射模M，S-1M是S-投射S-1R-模.

证明 设N为S-1M的循环子模，则存在M的循环子模N′，使得S-1N′=N.由M为S-投射模知，存在自由R-模f，和模同态φ:N′→F，π:F→M满足πφ(x)=x，∀x∈N′.从而

(S-1πS-1φ)(x)=x， ∀x∈N.

于是，S-1M是S-投射S-1R-模.

注 3.1 1) 如果M是平坦S-1R-模，则M是平坦R-模.

2) 如果M是f-投射S-1R-模，则M是f-投射R-模.

3) 一般地，如果M是投射(自由)S-1R-模，不能得到M是投射(自由)R-模.例如：Q是投射(自由)Q-模，但不是投射(自由)Z-模.

引理 3.3[10]设R为交换环，S⊂R为乘性子集，且不含零因子.如果M是S-投射S-1R-模，则M是S-投射R-模.

引理 3.4[11]设R是环.如果M是S-1R-模，则M≌S-1M.

命题 3.3 设R为交换环，S⊂R为乘性子集，且不含零因子.如果每个S-投射R-模都是平坦R-模，则每个S-投射S-1R-模都是平坦S-1R-模.

证明 设M是S-投射S-1R-模，则由引理3.3知，M是S-投射R-模，从而M是平坦R-模.由引理3.1知，S-1M是平坦S-1R-模.现证M是平坦S-1R-模.

设0→A→B为S-1R-模正合列，由引理3.4，有如图1所示的交换图.

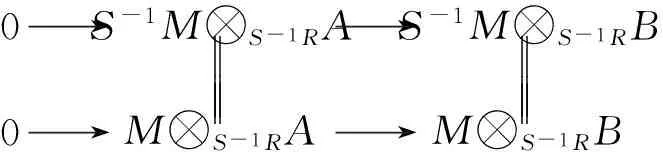
0→S-1M⊗S-1RA→S-1M⊗S-1RB0→M⊗S-1RA→M⊗S-1RB

图 1

从而，M是平坦S-1R-模.

4 S-投射模和S-平坦模

设M为右R-模.如果对于任意的有限生成自由R-模f，和f的任意循环子模C，都有

Tor1(M,F/C)=0，

则称MR为S-平坦的，等价地，对于每个有限生成自由左R-模的任意循环子模C，自然映射N⊗C→N⊗F是单同态.如果对于环R的任意有限子集X⊂R，annl(X)是有限生成左理想，则称R为左pseudo-凝聚的.对于S-平坦模，有以下结果：

命题 4.1 如果R是一个左pseudo-凝聚环，那么下列条件等价：

1) 每个S-平坦左R-模是投射的.

2)R是左凝聚左完全环.

证明 假设1)成立，则由文献[7]的推论2.11,R是左凝聚环.由于每个平坦左R-模都是S-平坦的，故每个平坦左R-模都是投射的，从而得到R是左完全环.

2)⟹1) 由R是左凝聚环可得，每个S-平坦左R-模是平坦的.再由R是完全环可知，每个S-平坦左R-模是投射的.

命题 4.2 如果R是右诺特环，则每个S-平坦右R-模是S-投射模.

证明 设MR为S-平坦模，NR≌R/I为M的循环子模，其中I⊂R为右理想.由诺特条件知，I有限生成.由文献[7]的引理2.4知，对任意的f:R/I→M，存在有限生成投射模f，和同态φ:R/I→F，和同态π:F→M，使得有如图2所示的交换图：

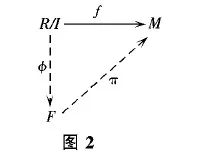
因此，MR是S-投射模.

定义 4.1[7]设R为环，如果R的每个左理想I，都存在非空子集X⊂R，使得I=annl(X)，则称R是一个左对偶环.

命题 4.3 如果R是对偶环，且每个任意X⊂R，ann(X)有限生成，则M是S-平坦模当且仅当M是S-投射模.

证明 因为R是对偶环，M为S-平坦模，所以，对于每个循环子模N⊂M，存在X⊂R，使得N≌R/annl(X)，再由annl(X)有限生成得，N为有限表现循环模，从而存在有限生成投射模f，和同态φ:N→F，ψ:F→M，使得ψφ=i，其中i是包含映射，即，M是S-投射模.

推论 4.1 如果R是QF-环，则每个S-平坦模都是S-投射模.

证明R是QF-环当且仅当R是左AFG-环，且R为左右对偶环[5].

5 S-投射模与投射模

如果对于任意有限生成子模N⊂M，存在自由模f，和R-模同态φ:M→F，π:F→M，满足

π(φ(x))=x， ∀x∈N，

则称MR为局部投射模.由文献[2],知道以下的事实：

引理 5.1[12]设R是任意的环，则以下条件等价：

1)R是左完全环;

2) 每个局部投射左R-模都是投射模;

3) 每个f-投射左R-模都是投射模.

那么，在什么条件下每个S-投射左R-模都是投射模呢？以下的结论给出了相应的条件：

命题 5.1 如果R是左凝聚左完全环，那么每个S-投射左R-模是投射的.

证明 由于每个S-投射左R-模都是S-平坦的，由上面的结论容易得到.

命题 5.2 设R是自内射环，则下列条件等价:

1)R是一个QF-环;

2) 每个S-投射R-模都是投射R-模;

3) 每个f-投射R-模都是投射R-模;

4) 每个局部投射R-模都是投射R-模.

证明 1)⟹2) 由1)可知，R是完全环，从而每个局部投射R-模都是投射模.再由自内射的条件和文献[10]的命题3可知，每个S-投射R-模都是投射模.

2)⟸1) 由于每个局部投射R-模都是S-投射模，故R是完全环，从而由自内射条件知，R是QF-环.

1)⟺3)⟺4)由引理5.1易知，因为R是QF-环当且仅当R是自内射完全环[13].

已知，如果M的任意有限生成子模都是平坦模，那么M是平坦模.类似的：

命题 5.3 如果M的每个循环子模都是投射模，那么M是S-投射模.

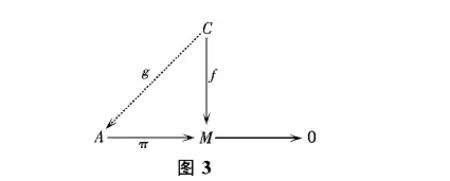
证明 设C是M的任意循环子模，由假设知，C是投射模，于是有如图3所示的交换图.

从而，M是S-投射模.

命题 5.4 设R为环，则下列条件等价：

1)S-投射右R-模的任意子模是S-投射模.

2)S-投射右R-模的任意循环子模是投射模.

证明 1)⟹2) 每个S-投射循环模都是投射模.

2)⟹1) 设M为S-投射R-模，N⊆M为任意子模，C为N的任意循环子模，因此也是M的循环子模.由2)知，C是投射模.再由命题5.3知，N是S-投射模.

6 S-投射模的直和

已知投射模关于直和封闭，而关于直积未必封闭.由于S-投射模是投射模的一种推广，考虑相似的性质.在文献[7]中，作者证明了，一个环R是左AFG-环当且仅当S-投射左R-模的任意直积仍然是S-投射的.在这里证明了以下的结论：

命题 6.1S-投射右R-模的任意直和是S-投射的.

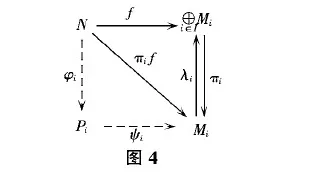
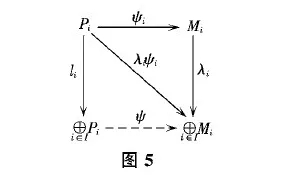
f.

[1] Jones M F. Flatness of f-projectivity of Torsionfree Modules and Injective Modules [C]//Lecture Notes in Math.New York: Springer-Verlag,1982:94-116.

[2] Azumaya G. Finite splitness and finite projectivity[J]. J Algebra,1987,106:114-134.

[3] Zhu S L. On rings over which every flat left module is finitely projective[J]. J Algebra,1991,139:255-261.

[4] Lam T Y. Lectures on Modules and Rings[M]. Berlin:Springer-Verlag,1999.

[5] Mao L X. A generalization of noetherian rings[J]. Taiwanese J Math,2007(12):501-512.

[6] Mao L X, Ding N Q. On divisible and torsionfree modules[J].Commum Algebra,2008,36:708-731.

[7] Mao L X, Ding N Q. New characterizations of pseudo-coherent rings[J]. Forum Math,2010,22:993-1008.

[8] 熊涛,王芳贵,胡葵. 余纯投射模与CPH环[J]. 四川师范大学学报:自然科学版,2013,36(2):198-201.

[9] Enochs E E, Jenda O M G. Relative Homological Algebra[M]. Berlin:Walter de Gruyter,2000.

[10] Couchot F. Flat modules over valuation rings[J]. J Pure Appl Algebra,2007,211:235-247.

[11] Rotman J J. An Introduction to Homological Algebra[M]. New York:Academic Press,1979.

[12] Zimmermann-Huisgen B. Pure submodules of direct products of free modules[J]. Math Ann,1976,224:233-245.

[13] Faith C, Huynh D V. When self-injective rings are QF: a report on a problem[J]. J Algebra Appl,2002(1):75-105.

[14] Anderson F W, Fuller K R. Rings and Categories of Modules[M]. New York:Springer-Verlag,1973.

[15] Bass H. Finistic dimension and a homological generalization of semi-prime rings[J]. Trans Amer Math Soc,1960,95:466-488.

[16] 蒋方明.f-投射模的直积和正向极限[J]. 南京理工大学学报,1993(6):58-60.

[17] Chase S U. Direct products of modules[J]. Trans Am Math Soc,1960,97:457-473.

[18] Cheniour F, Mahdou N. When every flat ideal is finitely projective[J]. Arabian J Math,2013(2):255-261.

[19] 王芳贵. 有限表现型模与w-凝聚环[J]. 四川师范大学学报:自然科学版,2010,33(1):1-9.

[20] Hajarnavis C R. On dual rings and their modules[J]. Commun Algebra,1985,93:253-266.

[21] Jones M F. F-projectivity and flat epimorphisms[J]. Commun Algebra,1981(9):1603-1616.

[22] Kato T. Self-injective rings[J]. Tohoku Math J,1967,19(4):485-495.

[23] Lam T Y. A First Course in Noncommutative Rings[M]. New York:Springer-Verlag,1991.

[24] Nicholson W K, Yousif M F. Quasi-Frobenius Rings[M]. New York:Cambridge University Press,2003.

2010 MSC：16D40; 16D70

(编辑 陶志宁)

On Singly Projective Modules

ZHANG Yongliang1, DING Nanqing2
(1.DepartmentofMathematicsandStatistics,AnkangCollege,Ankang725000,Shanxi;2.DepartmentofMathematics,NanjingUniversity,Nanjing210093,Jiangsu)

LetRbe a ring. Azumaya generalized the concept of projectivity of modules to single projectivity. The paper (Zhu S L. J Algebra,1991,139:255-261.) argued about rings over which every flat module is finitely projective. And the paper (Mao L X. Taiwanese J Math,2007(12):501-512.) gave a condition when every injectiveR-module is singly projective. This article shows some other relations between singly projectiveR-modules and other kinds of modules, such as quasi-injectiveR-modules, singly flatR-modules, finitely projectiveR-modules and divisibleR-modules. And it is proved that singly projective modules are closed under direct sums.

singly projective modules; flat modules; singly flat modules

2014-06-27

国家自然科学基金(11171240)和国家自然科学数学天元基金(11226057)

O153.3

A

1001-8395(2015)06-0846-05

10.3969/j.issn.1001-8395.2015.06.011

*通信作者简介：丁南庆(1963—),男,教授,主要从事环论、模论与同调代数的研究，E-mail:nqding@nju.edu.cn