EXISTENCE OF HOMOCLINIC SOLUTIONS TO NONAUTONOMOUS SECOND-ORDER p-LAPLACIAN SYSTEM WITH A COERCIVE POTENTIAL∗†

Yun Xin

(CollegeofComputerScienceandTechnology,HenanPolytechnicUniversity, Jiaozuo454000,Henan,E-mail:xy_1982@126.com)

Zhibo Cheng

(SchoolofMathematicsandInformationScience, HenanPolytechnicUniversity,Jiaozuo454000,Henan)

EXISTENCE OF HOMOCLINIC SOLUTIONS TO NONAUTONOMOUS SECOND-ORDER p-LAPLACIAN SYSTEM WITH A COERCIVE POTENTIAL∗†

Yun Xin

(CollegeofComputerScienceandTechnology,HenanPolytechnicUniversity, Jiaozuo454000,Henan,E-mail:xy_1982@126.com)

Zhibo Cheng

(SchoolofMathematicsandInformationScience, HenanPolytechnicUniversity,Jiaozuo454000,Henan)

In this paper,we investigate a non-autonomous second-orderp-Laplacian system. Based on critical point theory,we discuss the existence of homoclinic orbits of the system.

homoclinic solutions;p-Laplacian;coercive potential

2000MathematicsSubjectClassification34C37;58E05;70H05

1 Introduction

In this paper,we consider the existence of homoclinic orbits to the non-autonomous second-orderp-Lapcian system

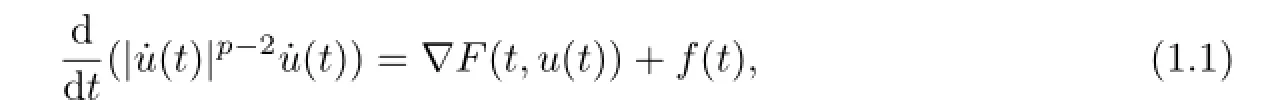
wherep＞1,t∈R,u∈RnandF:R×Rn→R andf:R→Rn.

As it is well known,a solutionu(t)to(1.1)is homoclinic(to 0)ifu(t)→0 and˙u(t)→0 as|t|→∞.In addition,ifu/≡0,thenuis called a nontrivial homoclinic solution.

The existence of homoclinic orbits is one of the most important problems in the theory of Hamiltonian systems.Recently the existence and multiplicity of homoclinic orbits to Hamiltonian systems have been studied extensively via critical point theory,such as[1-12]and the references therein.In particular,the second-order systems were considered in [2-5,8-10,12].

Whenp=2,(1.1)reduces to the following second-order Hamiltonian system

In[3],Izydorek and Janczewka proved the following theorem.

Theorem1.1[3]AssumethatandFandfsatisfythefollowingconditions:

(A1)F∈C1(R×Rn,R)isT-periodicwithrespecttot,T＞0;

(A2)thereisaconstantb＞0suchthatforall(t,x)∈R×Rn,

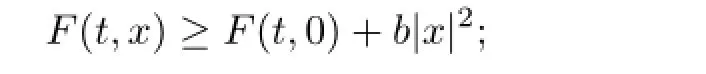
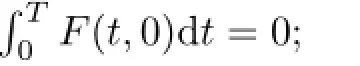
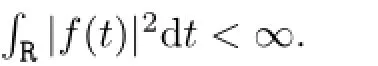
Thensystem(1.2)possessesahomoclinicsolution

In[9],Tang and Xiao further investigated the existence of homoclinic solutions to(1.1). And the following theorem was obtained.

Theorem1.2[9]AssumethatFsatisfies(A1)andthefollowingconditions:

(B2)Thereareconstantsb＞0andµ＞1suchthatforall(t,x)∈[0,T]×Rn,

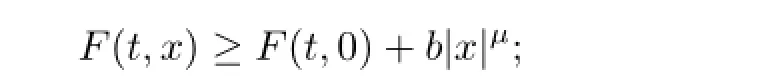
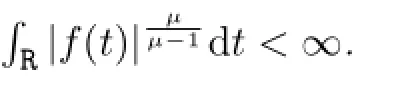
Then(1.1)possessesahomoclinicsolution.

Clearly,either assumption(A2)in Theorem 1.1 or assumption(B2)in Theorem 1.2 implies that the coercive condition

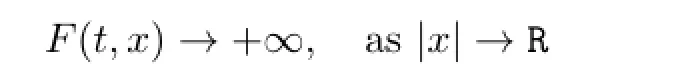
holds,which is crucial for obtaining the existence of homoclinic solution to(1.2)and(1.1) in[3,9],respectively.In this paper,we continuously investigate the existence of homoclinic solutions to(1.1),and our result generalizes the above results.

Our goal in this paper is to use the following more general conditions instead of(B2), such asFcan change sign when|x|is small enough.

(C2)There are constantsb＞0,ν＞1 andµ＞νsuch that for all

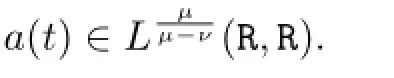
Next,we present our main result.

Theorem1.3AssumethatFandfsatisfyassumptionsThen system(1.1)possessesahomoclinicsolution

In order to receive a homoclinic solution to(1.1),similarly to[3],we consider a sequence of diff erential system:

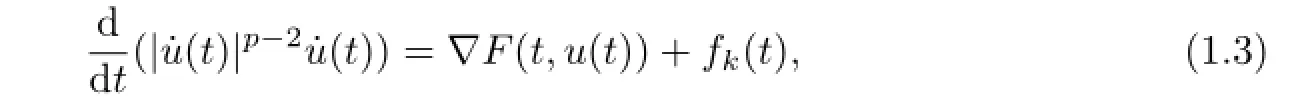
wherefk:R→Rnis a 2kT-periodic extension offin the interval

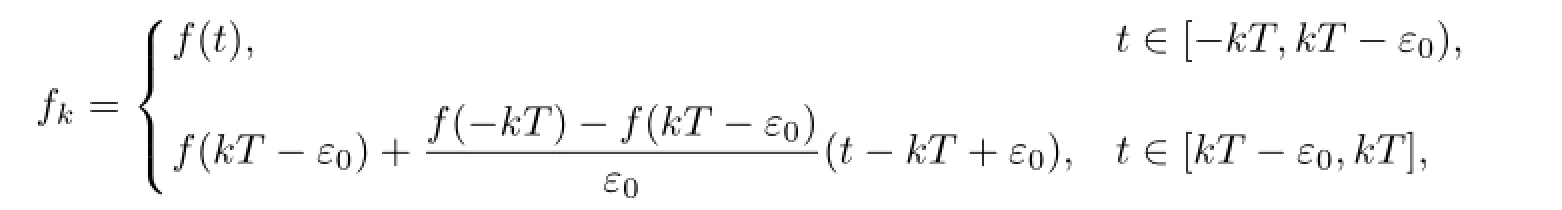
ε0∈(0,min{1,T})is a constant independent ofk.We will prove the existence of one homoclinic solution to(1.1)similar to that of the limit of the 2kT-periodic solutions to(1.3) in[3].However,some technical details in this paper are diff erent form that in[3].

2 Proof of Theorem 1.3

For eachk∈N,letdenote the Hilbert space of 2kT-periodic functions on R with values in Rnunder the norm

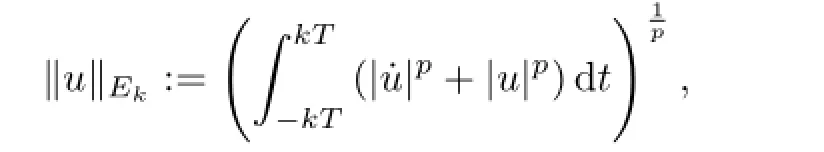
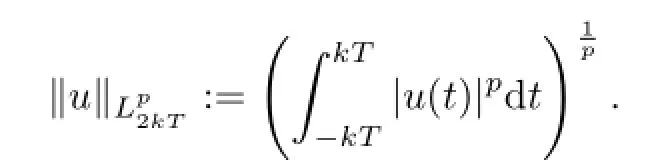
Then we can easily check thatis a weakly lower semi-continuous and

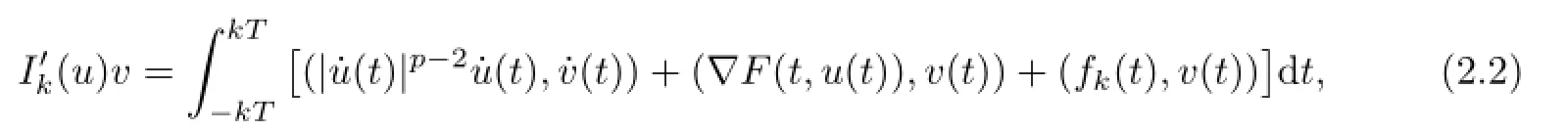
for allu,v∈Ek.Furthermore,it is well known that the critical points ofIkinEkare classical 2kT-periodic solutions to(1.3).

Based the follows lemmas,Theorem 1.3 obviously holds.

Lemma2.1[9]Leta＞0andu∈W1,p(R,Rn).Thenforeveryt∈R,thefollowing inequalityholds:

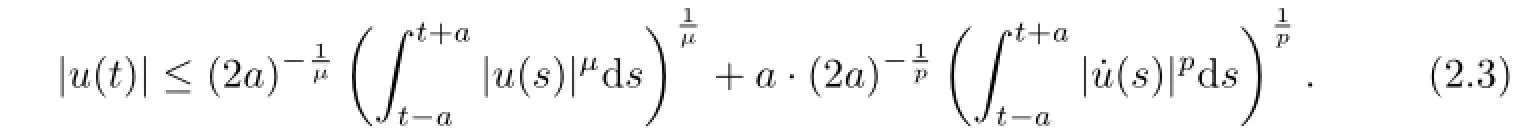
Lemma2.2[9]Letu∈Ek.Thenthefollowinginequalityholds:

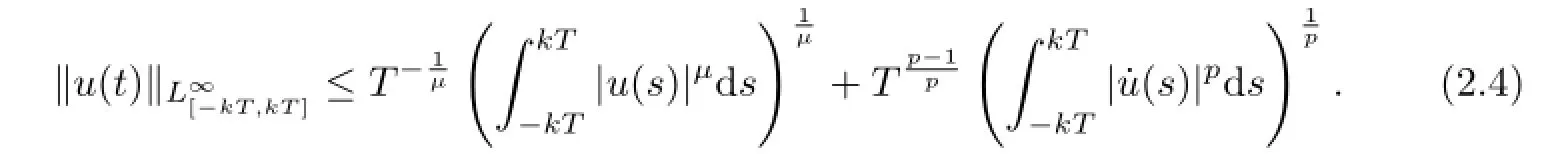
Lemma2.3AssumethatFandfsatisfy(A1),(C2)and(B3).Thenforeveryk∈N, system(1.3)possessesa2kT-periodicsolutionuk∈Eksuchthat

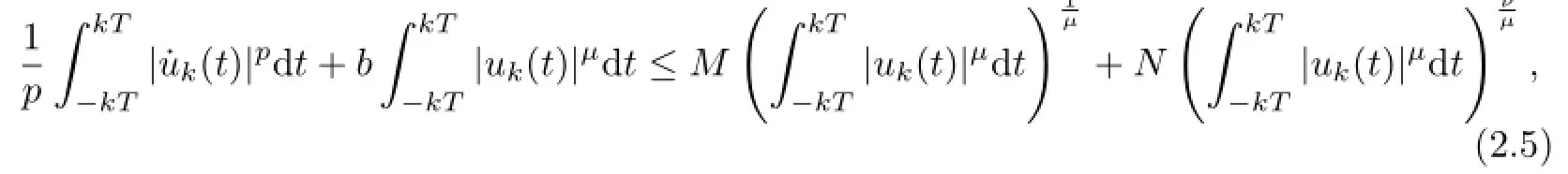
where

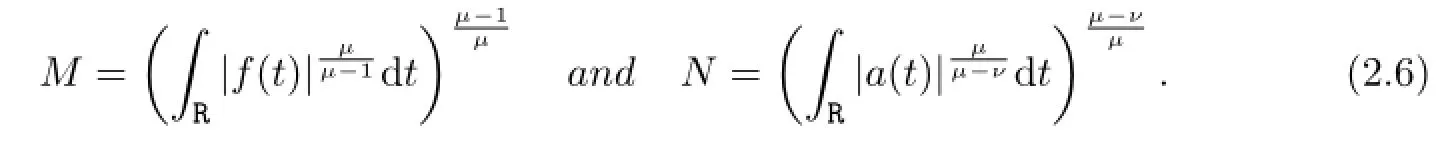
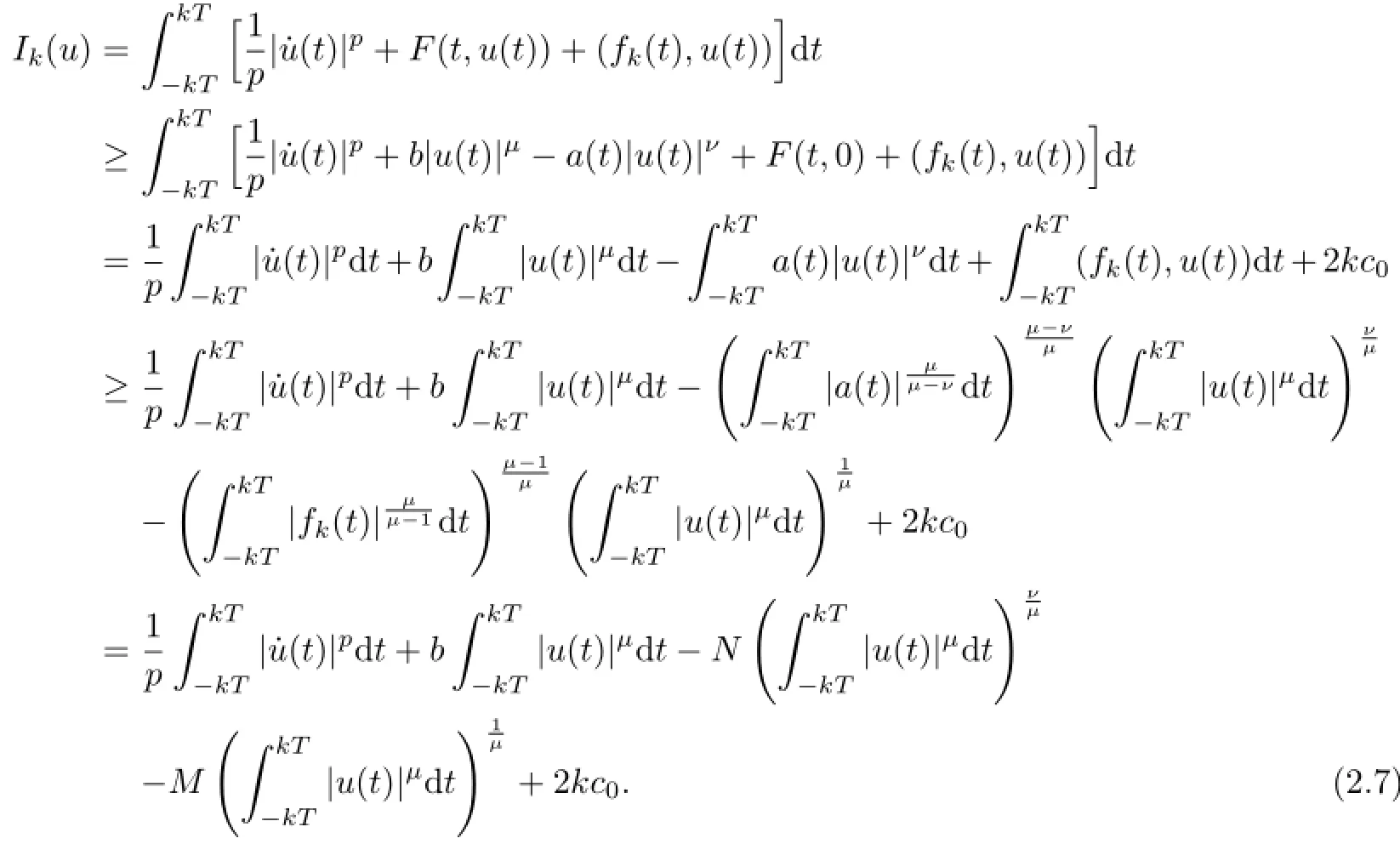
Set

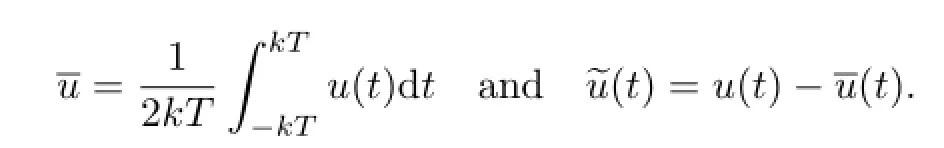
Then by Sobolev’s inequality,we have

In view of(2.9),it is easy to verify,for eachk∈N,that the following conditions are equivalent:

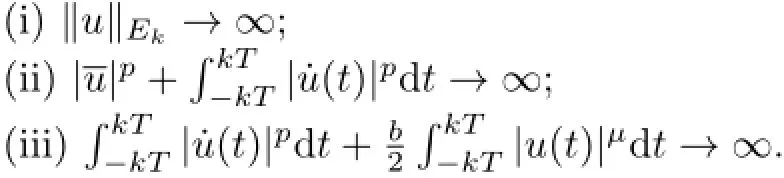
Hence,form(2.8),we obtain

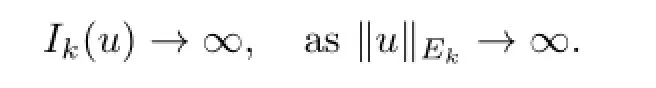
Now by Theorem 1.1 and Corollary 1.1 in[13],we conclude that for everyk∈N there exists auk∈Eksuch that

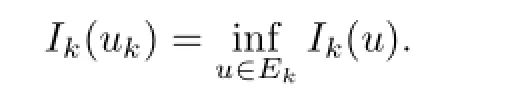
Since

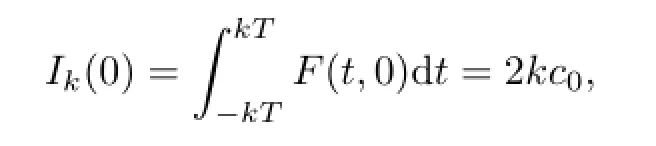
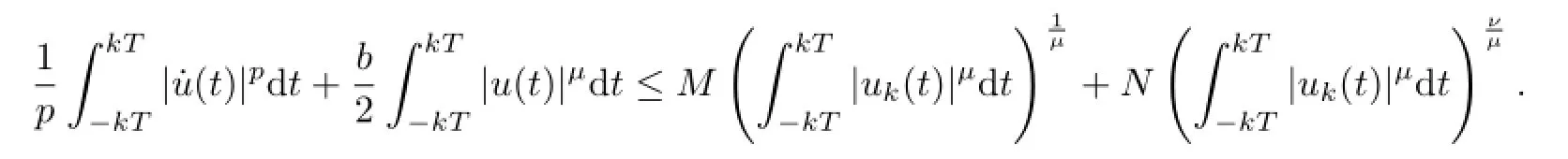
This completes the proof.

Lemma2.4Letuk∈Ekbeasolutiontosystem(1.3)whichsatisfies(2.5)fork∈N. ThenthereexistsapositiveconstantCindependentofksuchthat

ProofBy(2.5),we can see that

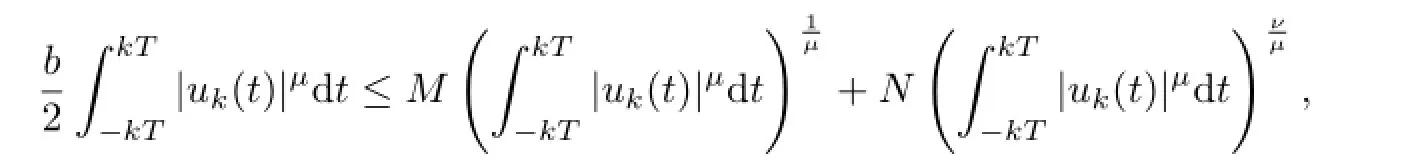
which implies that there is anM1＞0 independent ofksuch that

From(2.5)and(2.11),we obtain

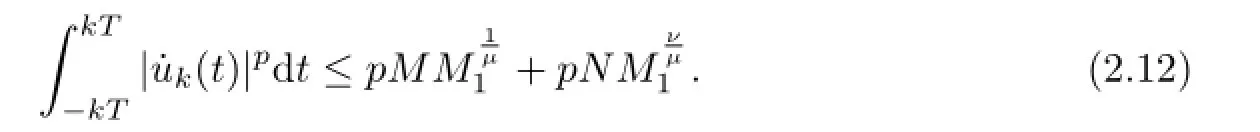
It follows from(2.4),(2.11)and(2.12)that

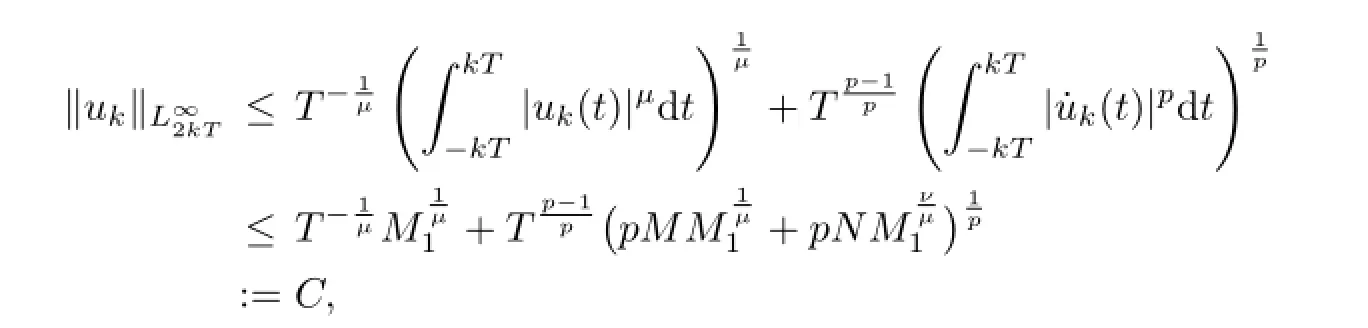
which shows that(2.10)holds.The proof is complete.

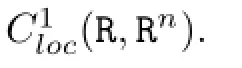
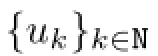
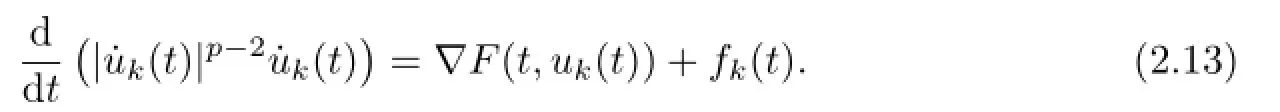
From(2.10),(2.13),(A1)and(B3),we obtain

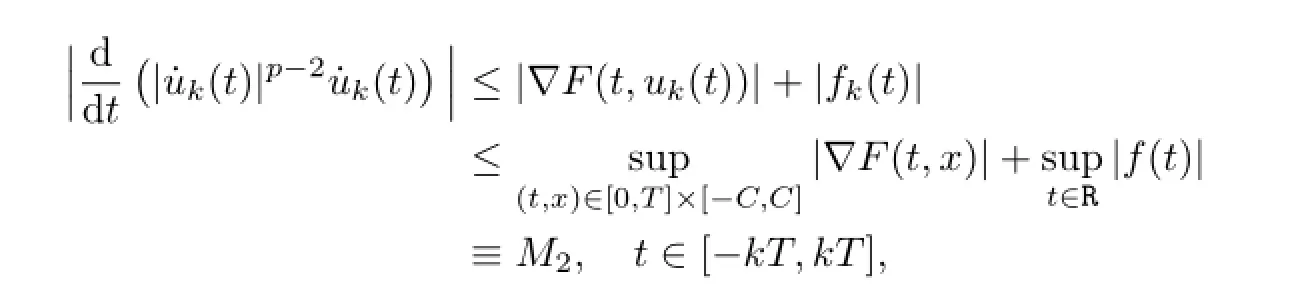
which implies that

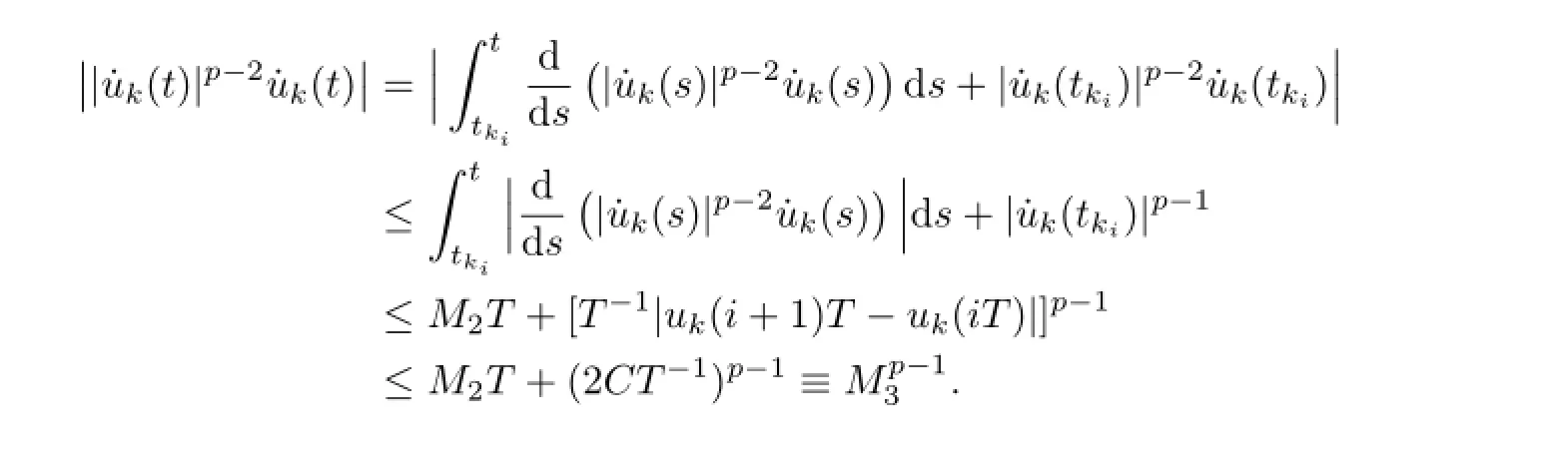
Consequently,

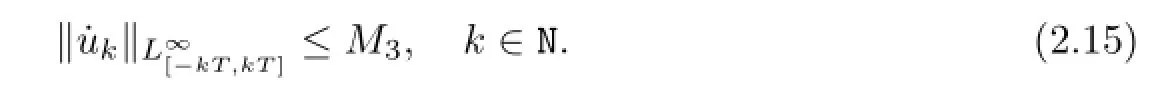
We claim thatis also equicontinuous.If not,then there exist anε0＞0,two sequencesand a sequenceof integers such that

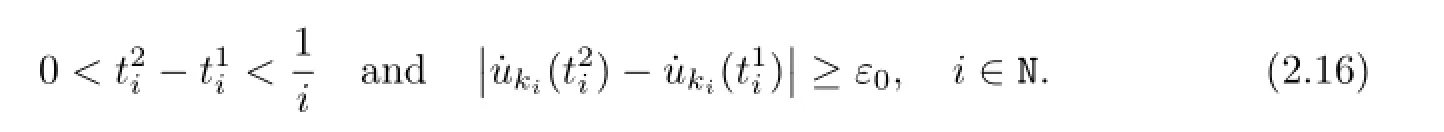
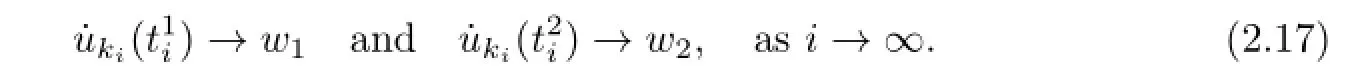
Combining(2.16)with(2.17),we have

On the other hand,from(2.14)and(2.16),we have

Lemma2.6LetbedeterminedbyLemma2.5.Thenu0isasolutionto(1.1)suchthatu0(t)→0and˙u0→0ast→±∞.

ProofStep 1We will show thatu0(t)satisfi es(1.1).By Lemmas 2.3 and 2.5,we have

Takea,b∈R such thata＜b.There exists aj0∈N such that for allj＞j0

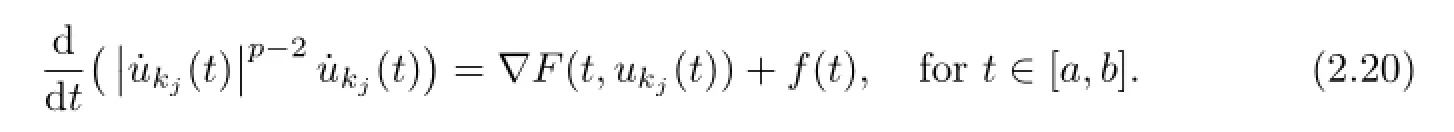
Integrating(2.20)fromatot∈[a,b],we have

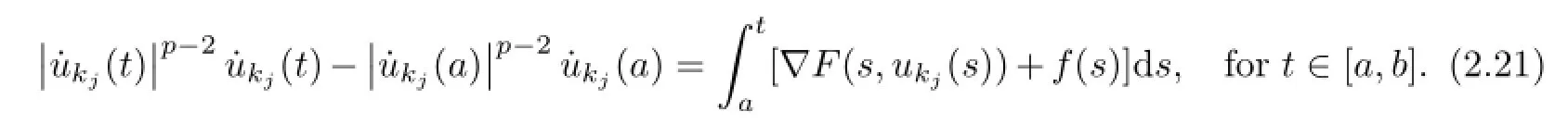
Note that Lemma 2.5 shows thatukj→u0uniformly on[a,b]anduniformly on [a,b]asj→∞.Letj→∞in(2.21),then we get

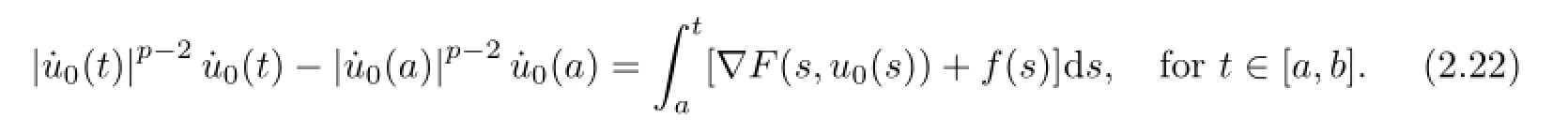
Sinceaandbare arbitrary,(2.22)shows thatu0(t)is a solution to(1.1).

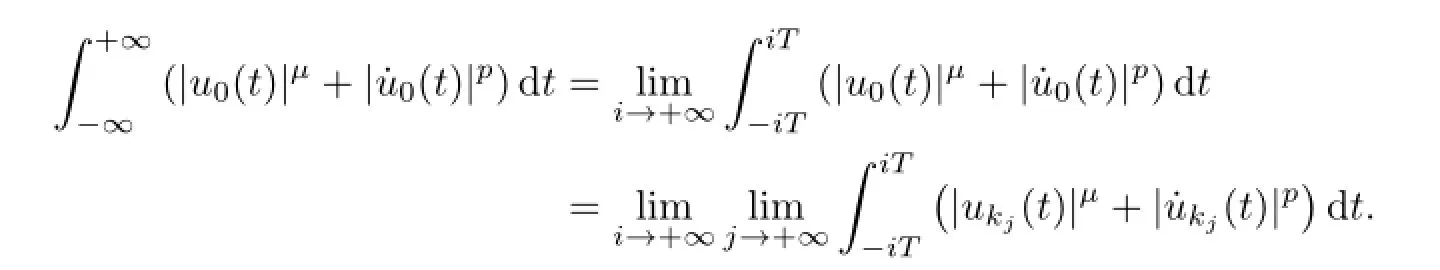
Obviously,for everyi∈N,there exists aj1∈N such that for allj＞j1we have

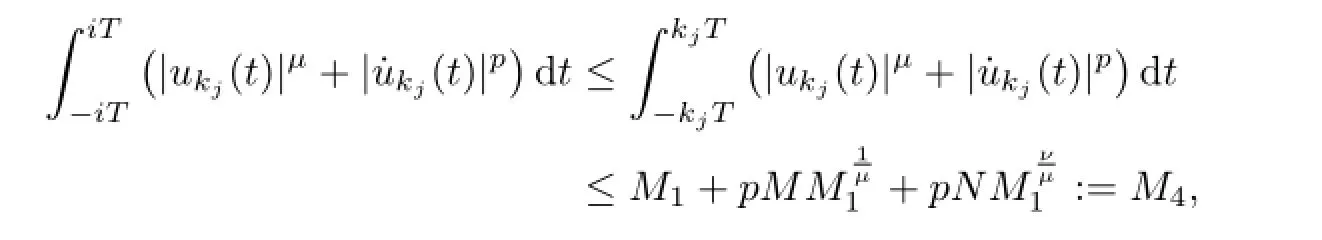
by(2.11)and(2.12).Lettingj→+∞,we get

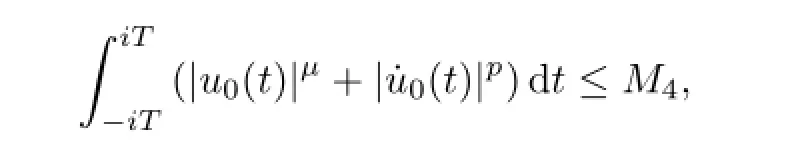
next lettingi→+∞,we have

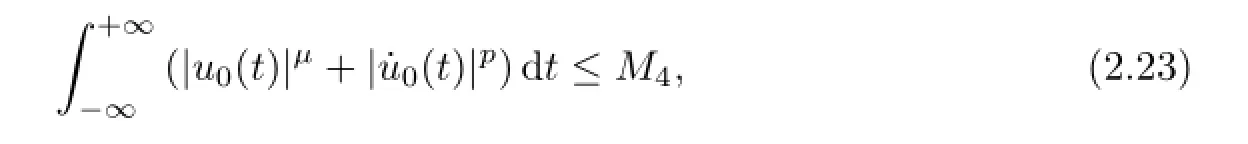
so

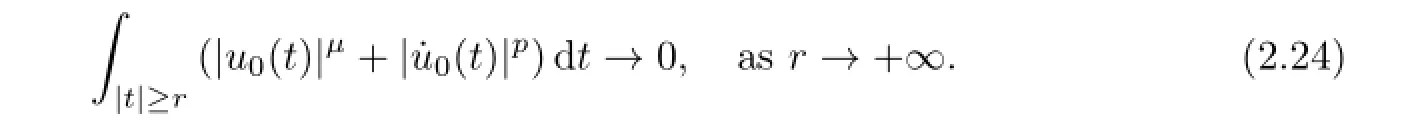
By(2.3),we obtain

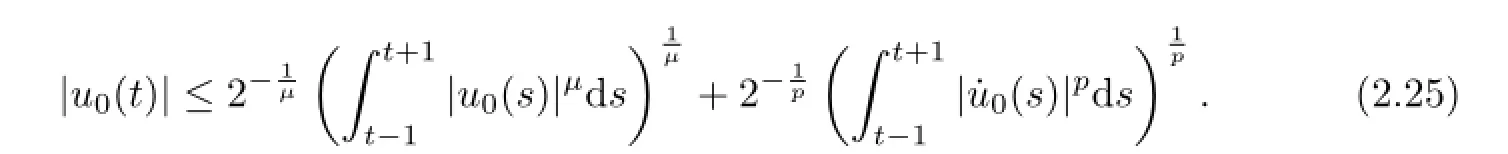
Combining(2.24)and(2.25),we receive,as

Step 3Finally,we will show that

From(2.10)and Lemma 2.5,we have

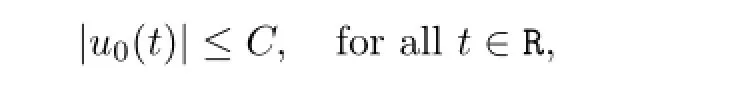
which together with(1.1),(A1)and(B3)imply that

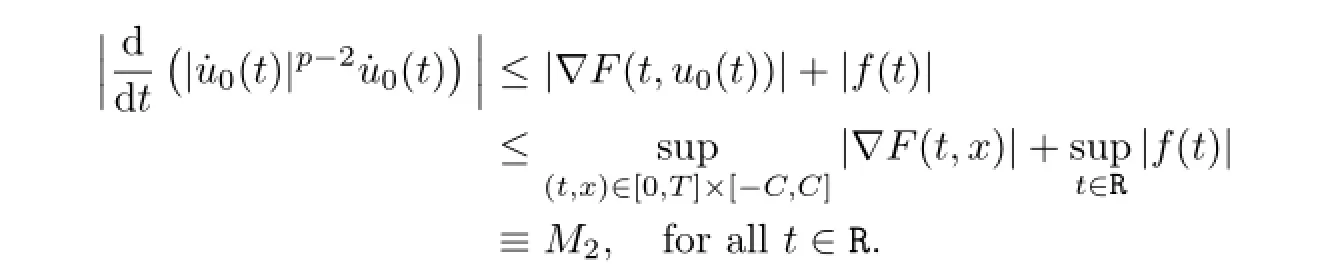
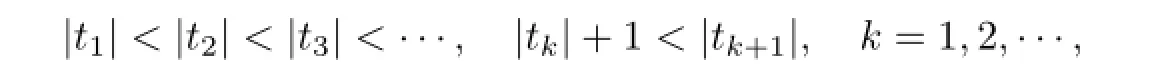
and

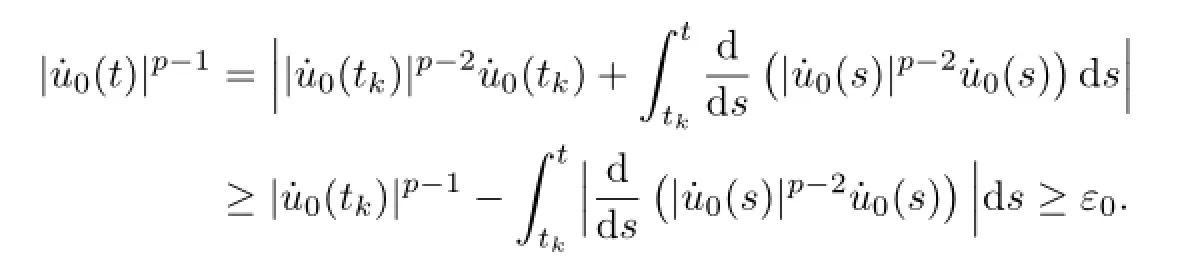
It follows that

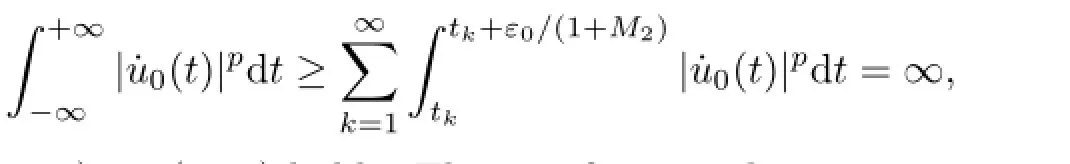
which contradicts(2.23),so(2.26)holds.The proof is complete.

[1]C.O.Alves,P.C.Carriao,O.H.Miyagaki,Existence of homoclinic orbits for asymptotically periodic system involving Duffi ng-like equation,Appl.Math.Lett.,16:5(2003),639-642.

[2]V.Coti-Zelati,P.H.Rabinowitz,Homoclinic orbits for second order Hamiltonian systems possessing superquadratic potentials,J.Amer.Math.Soc.,4:4(1991),693-727.

[3]M.Izydorek,J.Janczewska,Homoclinic solutions for nonautonomous second-order Hamiltonian systems with a coercive potential,J.Math.Anal.Appl.,335:6(2007),1119-1127.

[4]M.Izydorek,J.Janczewska,Homoclinic solutions for a class of the second order Hamiltonian systems,J.DifferentialEquations,219:4(2005),375-389.

[5]X.Lv,S.P.Lu,P.Yuan,Homoclinic solutions for nontantonomous second-order Hamiltonian systems with a coercive potential,NonlinearAnalysisTMA,72:10(2010),3484-3490.

[6]P.H.Rabinowitz,Homoclinic orbits for a class of Hamiltonian systems,Proc.Roy.Soc.Edinburgh.Sect.A,114:2(1990),33-38.

[7]E.S´er´e,Existence of infi nitely many homoclinic orbits in Hamiltonian system,Math.Z.,209:1(1992),27-42.

[8]J.T.Sun,H.B.Chen,J.J.Nieto,Homoclinic solutions for a class of subquadratic second-order Hamiltonian systems,J.Math.Anal.Appl.,373:1(2011),20-29.

[9]X.H.Tang,L.Xiao,Homoclinic solutions for ordinaryp-Laplacian systems with a coercive potential,NonlinearAnalysisTMA,71:3(2009),1124-1132.

[10]X.H.Tang,L.Xiao,Homoclinic solutions for nonautonomous second-order Hamiltonian systems with a coercive potential,J.Math.Anal.Appl.,351:2(2009),586-594.

[11]Y.X.Xu,M.Y.Huang,Homoclinic orbits and Hopf bifurcations in delay diff erential systems with T.B singularity,J.DifferentialEquations,244:3(2008),582-598.

[12]Z.H.Zhang,R.Yuan,Homoclinic solutions for some second order non-autonomous Hamiltonian systems without the globally superquadratic condition,NonlinearAnalysisTMA,72:5(2010),1809-1819.

[13]J.Mawhin,M.Willem,Critical Point Theory and Hamiltonian Systems,Appl.Math.Sci,vol. 74 Springer-Verlag,New York,1989.

(editedbyLiangweiHuang)

∗This research was supported by NNSF of China Project(No.11326124)and Education Department of Henan Province Project(No.14A110002).

†Manuscript received January 21,2015