ALMOST PERIODIC SOLUTIONS TO STOCHASTIC FRACTIONAL PARTIAL EQUATIONS IN FRACTIONAL POWER SPACE∗†

Xiaoqing Wen,Licheng Ge,Hongwei Yin

(1.SchoolofScience,NanchangUniversity,Nanchang330031, 2.InstituteforAdvancedStudy,NanchangUniversity,Nanchang330031)

ALMOST PERIODIC SOLUTIONS TO STOCHASTIC FRACTIONAL PARTIAL EQUATIONS IN FRACTIONAL POWER SPACE∗†

Xiaoqing Wen1,Licheng Ge2,Hongwei Yin1‡

(1.SchoolofScience,NanchangUniversity,Nanchang330031, 2.InstituteforAdvancedStudy,NanchangUniversity,Nanchang330031)

In this paper,we prove the existence ofpth moment almost periodic mild solutions in fractional power space to a class of stochastic fractional partial equations using the techniques of contraction fi xed point principle,Schauder fixed point theorem and semigroup theorem.

stochastic fractionaldiff erentialequation;pth moment almost periodic solution

2000MathematicsSubjectClassification34K50;60H10

1 Introduction

Fractional diff erential equations have drawn much attention because of their application in many important fields[1],such as engineering,mechanics,material and chemistry and so on.At present,a lot of significant development has been taken in ordinary and partial diff erential equations including fractional derivatives,refer to the literatures[2-7]and the references therein.Furthermore,in[8,9],Zhou and Agarwal et al respectively discussed the existence and the uniqueness of solutions to fractional neutral diff erential equations with delay by Kransnoselskii’s fixed point theorem.In[10]Benchohra et al showed the existence of solutions to fractional functional diff erential equations with infinite delay by the Banach fixed theorem and the Leray-Schauder degree theorem.In[11],Jankowski proved that the existence results of an ordinary fractional equations with Volerra integral by the Banach fixed theorem and a monotone iterative method.

Besides,almost periodicity is important in probability for investigating stochastic processes[12],which is applied in mathematicalphysics and statistics.The concept of quadratic mean almost periodicity was introduced by Bezandry and Diagana[13].Afterwards such a concept became a standard tool to be applied in investigating the existence and uniqueness of a quadratic mean almost periodic solution to stochastic evolution equations.By fi xed point principle,Cao et al studied the quadratic mean almost periodic solution of a class of stochastic functional partial diff erential equations[14].In addition,quadratic mean almost periodic solutions of neutralstochastic evolution equations with infi nite delay has beenrecently obtained in[15].Moreover,Wang and Liu obtained the quadratic mean almost periodic solutions to stochastic diff erentialequations with L´evy noise[16].However,few author, as far as we know,investigatedpth moment almost periodic solutions to fractional stochastic evolution diff erential equations.To this end,in this paper we make the fi rst attempt to fill this gap and studypth moment almost periodic solution to the following forms:

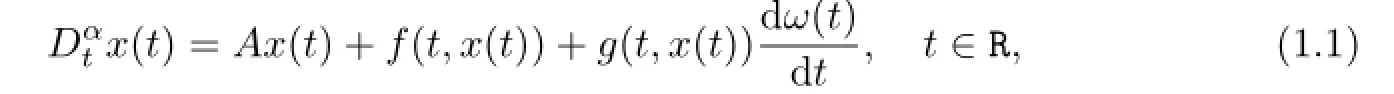
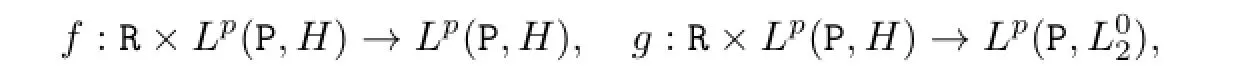
wherep≥2 throughout this paper.

In this paper we show the existence ofpth moment almost periodic solutions to(1.1) in fractional power space.The rest of this paper is organized as follows:in Section 2,we introduce some notations,concepts and basic results.In Section 3,the main results are present.In Section 4,we give an example to illustrate our results.

2 Preliminaries

In this section,we introduce some notations,defi nitions,lemmas and preliminary facts which are used in what follows.Throughout this paper,(H,‖·‖)and(K,‖·‖)denote real Hilbert spaces.Let(Ω,F,P)be a complete probability space andL2(K,H)be the space of all Hilbert-Schmidt norm‖·‖2.For a symmetric nonnegative operatorQ∈L2(K,H)with finite trace we suppose that{ω(t):t∈R}is aQ-Wiener process defi ned on(Ω,F,P)with values inK.

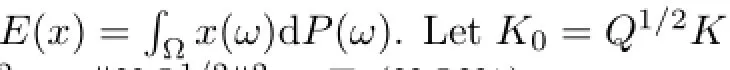
Let 0∈ρ(A)whereρ(A)is the resolvent ofA.Then forγ∈(0,1],it is possible to defi ne the fractional power(A)γ,as a closed linear operator on its domainD((A)γ).Furthermore, the subspaceD((A)γ)is dense inHand the expression

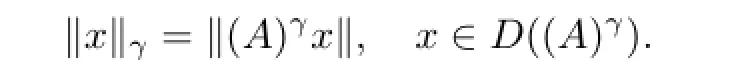
We introduce the following lemma[17].

Lemma2.1[17]Let0＜γ≤µ≤1.Thenthefollowingpropertieshold:

(i)Lp(P,Hµ)isaBanachspaceandLp(P,Hµ)→Lp(P,Hγ)iscontinuous;

(ii)thefunctions→(A)γG(t)iscontinuousintheuniformoperatortopologyon(0,∞)andthereexistsanMγ＞00;

(iii)foreachx∈D((A)γ)andt≥0,(A)γG(t)x=G(t)(A)γx;

(iv)(A)-γisaboundedlinearoperatorin

Definition2.1Caputo’s derivative of orderqwith the lower limit 0 for the functionh:[0,∞)→R can be written as

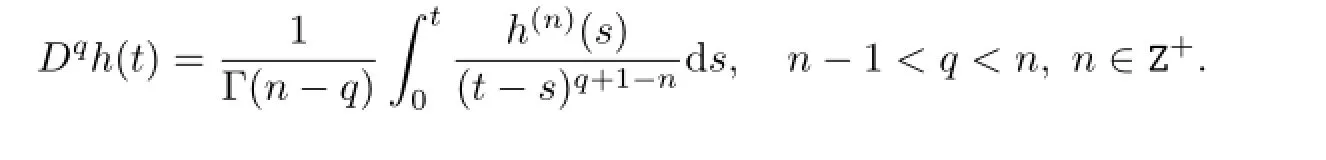
Definition2.2A stochastic processx:R→Lp(P,H)is said to be continuous whenever

Definition2.3A continuous stochastic processx:R→Lp(P,H)is said to bepth moment almost periodic if for eachε＞0 there exists anl(ε)＞0 such that any interval of lengthl(ε)contains at least a numberτfor which

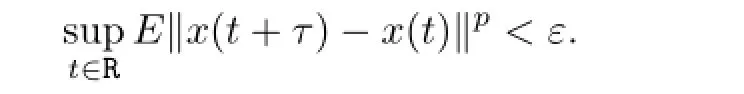
The collection of all stochastic processesx:R→Lp(P,H)which arepth almost periodic is denoted byAP(R,Lp(P,H)).

Lemma2.2[13]IfxbelongstoAP(R,Lp(P,H)),then:

(i)Themappingt→E‖x(t)‖pisuniformlycontinuous;

(ii)thereexistsaconstantN＞0,suchthatE‖x(t)‖p≤N,foreacht∈R;

(iii)xisstochasticallybounded.

Lemma2.3[13]AP(R,Lp(P,H))⊂CUB(R,Lp(P,H))isaclosedsubspace.

Lemma2.4[13]AP(R,Lp(P,H))isaBanachspaceendowedwiththenorm:

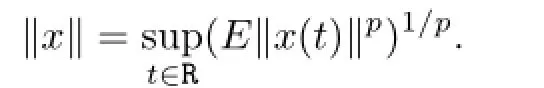
Definition2.4[13]A functionF:R×Lp(P,Y)→Lp(P,Z),(t,y)→F(t,y),which is jointly continuous,is said to bepth moment almost periodic int∈R uniformly iny∈BwhereB⊂Lp(P,Y)is compact if for anyε＞0,there exists anl(ε,B)＞0 such that any interval of lengthl(ε,B)contains at least a numberτfor which

for each stochastic processy:R→B.

Lemma2.5[18]IffsatisfiesauniformH¨oldercondition,withexponentβ∈(0,1],then theuniquesolutiontothefollowingCauchyproblem:{

isgivenby

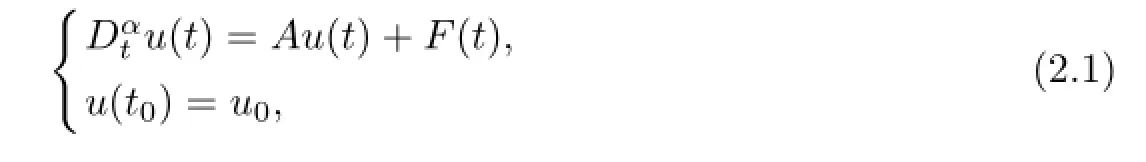
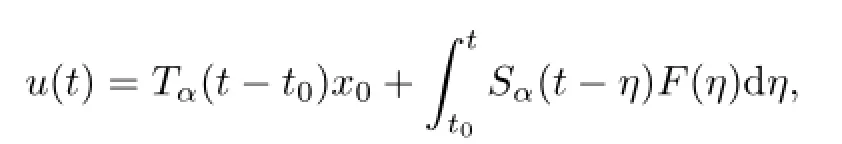
where

andζαisaprobabilitydensityfunctionζαdefinedon[0,∞)[18,19],andΓisacontour startingandendingat-∞.

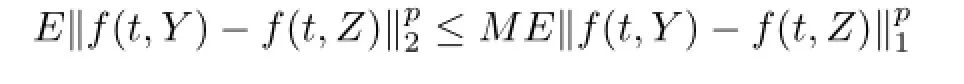
Lemma2.6[13]Letf:beapthmoment almostperiodicprocessint∈RuniformlyinY∈K,whereiscompact. SupposethatfisLipschitzinthefollowingsense:forallY,Z∈Lp(P,B1)andforeacht∈R,whereM＞0.Thenforanypthmomentalmost periodicprocessΦ:R→Lp(P,B1),thestochasticprocesst→f(t,Φ(t))ispthmoment almostperiodic.

Definition2.5AnFt-progressive processis called a mild solution to(1.1)if fort∈[0,T]

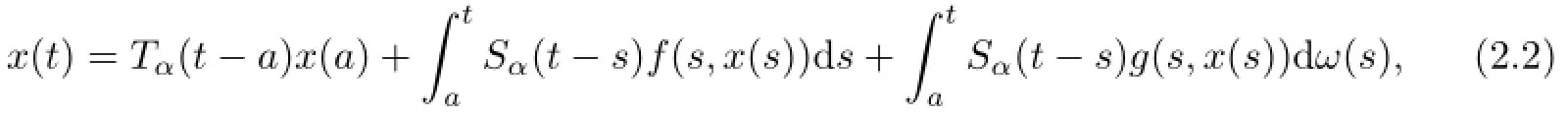
for allt≥aand for eacha∈R.

3 Main Results

In this section,we give our main results.Firstly,we need the following assumptions:

(A1)The operatorA:D(A)⊂Lp(P,H)→Lp(R,H)is the infi nitesimal generator of an analytic semigroup of linear operators{G(t)}t≥0onLp(P,H)andM,δare positive numbers such that‖G(t)‖≤Me-δtfort≥0.

(A2)There exists a positive numberγ∈(0,1),such thatis apth moment almost periodic int∈R uniformly inwhich is a compact subspace.Moreover,fis Lipschitz in the following sense:There exists anl1＞0 such that

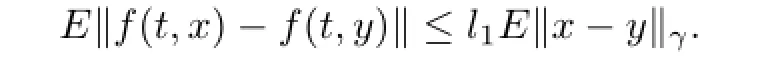
(A3)The functiongispth moment almost periodic int∈R uniformly inx∈B2,where B2⊂Lp(P,H)is a compact subspace.Moreover,gis Lipschitz in the sense that:There exists anl2＞0 such that

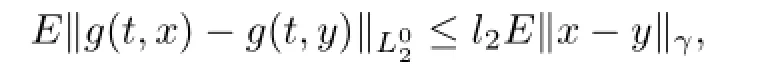
for allt∈R and for each stochastic processesx,y∈Lp(P,H).

Theorem3.1Assumethatconditions(A1)-(A3)aresatisfied.Then(1.1)hasaunique quadratic-meanalmostperiodicmildsolutionprovided

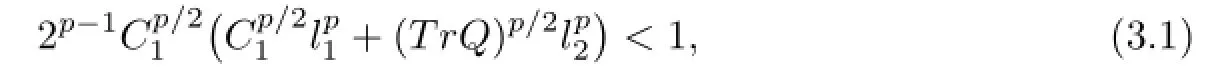
where

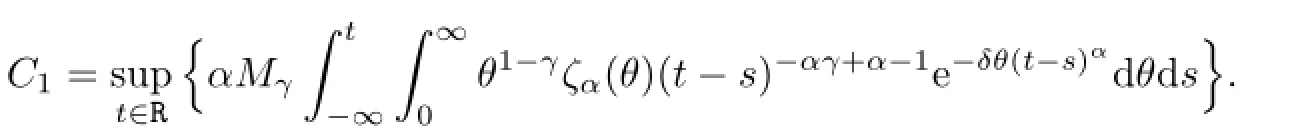
ProofWe defi ne an operatorLonby

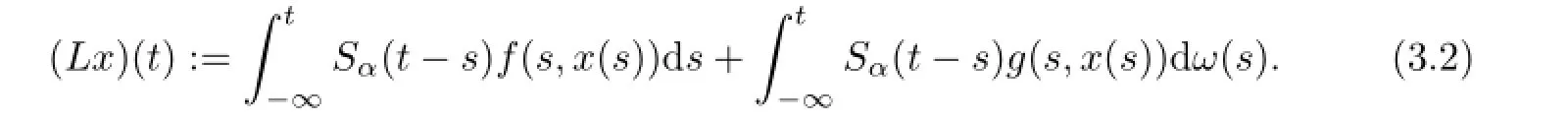
Note that(3.2)is well-defi ned and satisfies(2.2)for allt≥awith eacha∈R.

Defi ne

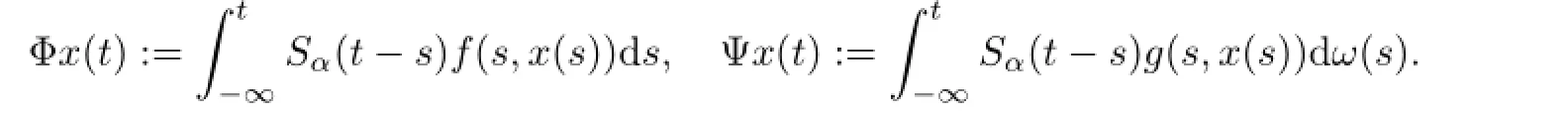
First,we show thatΦx(t)ispth moment almost periodic wheneverxispth moment almost periodic.In fact,we suppose thatxispth moment almost periodic and using(A2) and Lemma 2.6,one can easily see thats→f(s,x(s))ispth moment almost periodic. Therefore,it follows from Definition 2.3 that for anyε＞0,there exists anl(ε)＞0 such that every interval of lengthl(ε)contains at least a numberτwith the property that

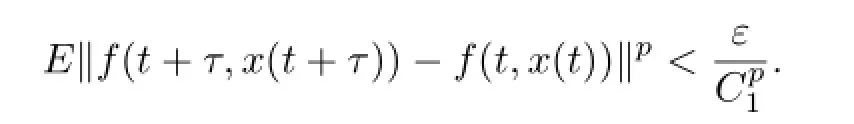
Now,by H¨older inequality we consider

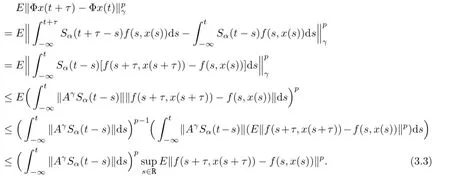
By the properties of the probability density functionζα[18,19],we conclude that the following integration function

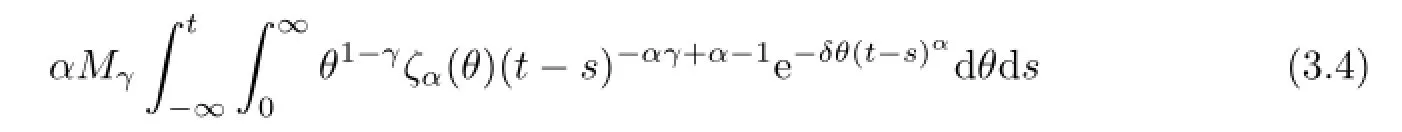
has a upper bound denoted byC1.

Then in view of(3.4),we can conclude that

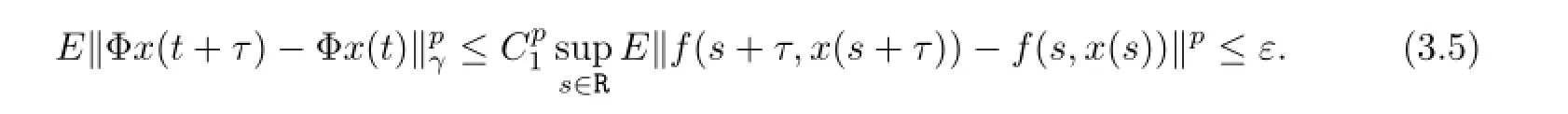
Hence,Φx(·)ispth moment almost periodic.

Next,by Lemma 2.6,one can also easily see thatis apth moment almost periodic.Therefore,it follows from Definition 2.3 that for anyε＞0,there exists anl(ε)＞0 such that every interval of lengthl(ε)contains at least a numberτwith the property that

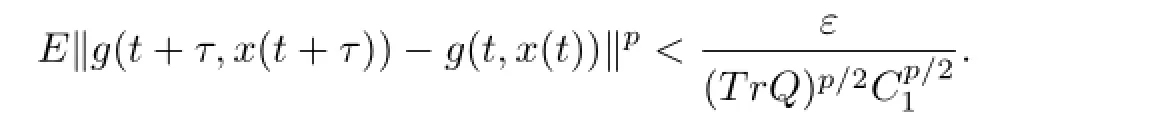
Therefore,by an estimate on Itˆo integral established in Ichikawa[20]and(A3),we have

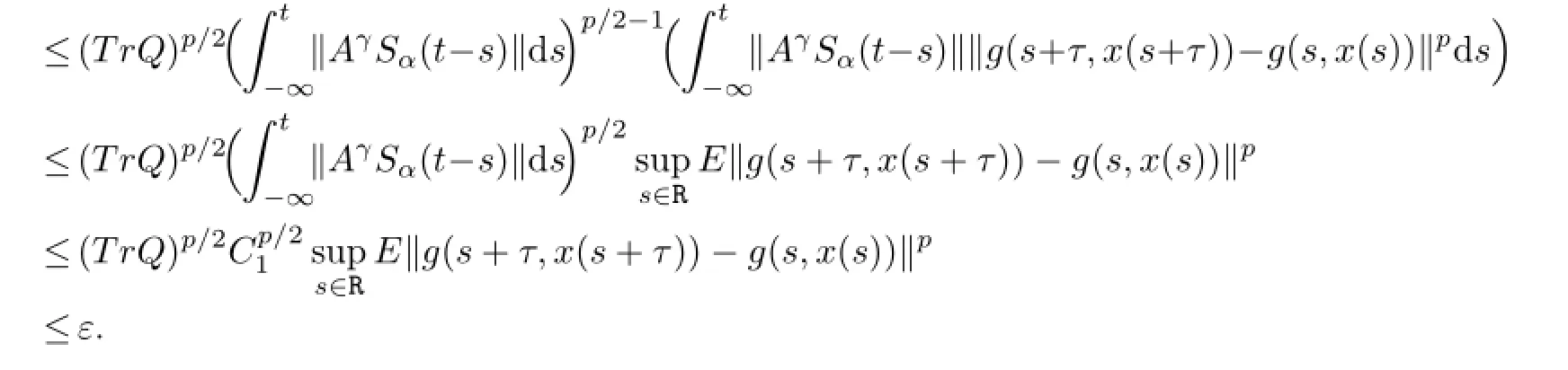
ThusΨx(·)ispth moment almost periodic.It is clear thatLmapsinto itself.

Now,we prove thatLis a strict contraction onIndeed,for eacht∈R,we have

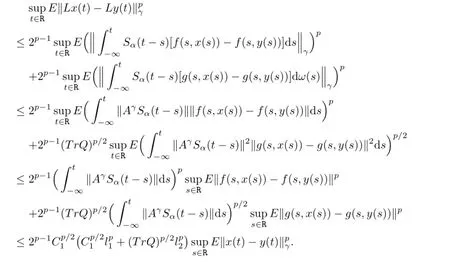
Hence,by(3.1)we know thatLis a contraction map.So by the contraction principle,we conclude that there exists a unique fixed pointx(·)forLinWe complete this proof.

Now we give another main result by Schauder fixed point theorem.In this sequence,we require the following assumptions:

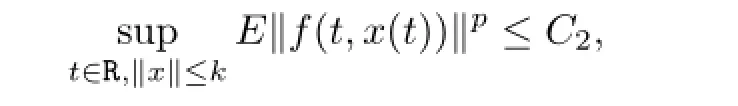
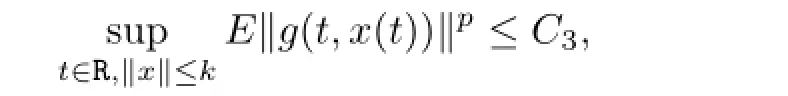
Theorem3.2Let(A4)and(A5)besatisfied.Then(1.1)hasatleastonepthmoment almostperiodicmildsolution.

ProofLetLbe the function defi ned by(3.2).To prove this theorem,it is enough to show thatLis a compact map.Next,we give several steps.

Setp 1Lis continuous.

Letbe a sequence such thatxn→x.This,together with the continuity off(t,x(t)) andg(t,x(t))with respect toxandt,respectively,implies thatandasn→∞.For eacht∈[0,T],using the proof method of Theorem

3.1 we have

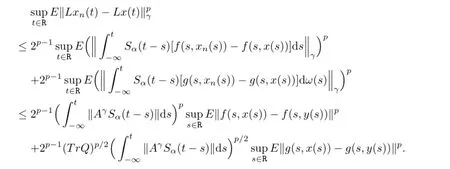
This follows thatLis continuous.

Step 2Lmaps bounded sets into bounded sets.

For eachk∈N,letWe show that there exists ak∗∈N such thatIf it is not true,then for eachk∈N,there existxk∈Bkandxk∈[0,T]such thatBy(A1)and(A2),we have

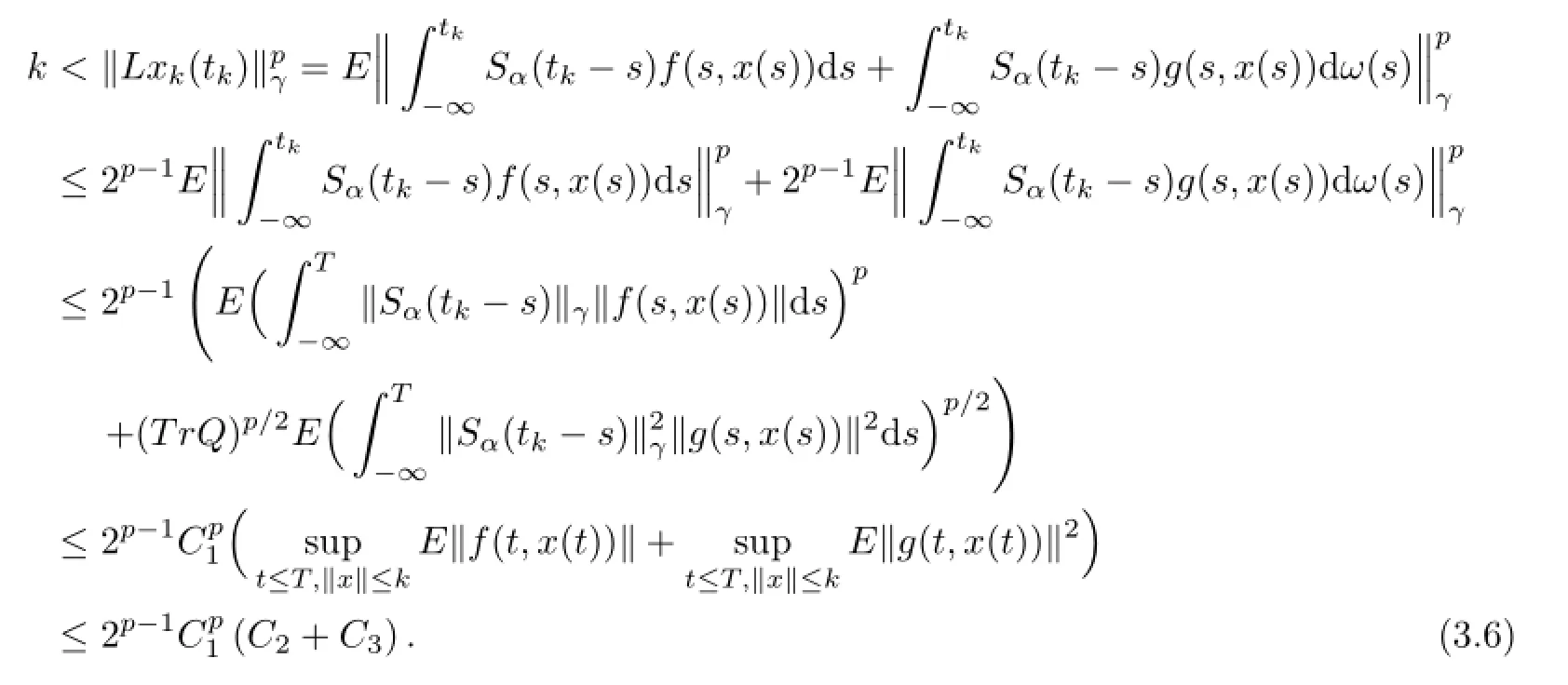
Dividing both sides of(3.6)bykand taking it suffi cient large,it follows that

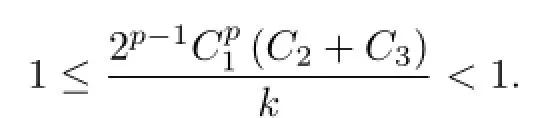
This is a contradiction.Thusfor some

Step 3Lmaps bounded sets into equicontinuous sets.Letbe a bounded set as in Step 2,andx∈Bk∗.Then

Thus the Arzela-Ascoli theorem implies thatLBk∗is relatively compact andLis completely continuous onBk∗.By Schauder fixed point theorem,we deduce thatLhas a fi xed point inBk∗which is apth moment almost periodic mild solution to(1.1).This proof is completed.

4 Example

In this section,we give an example to illustrate our main results.Now,we consider the following syste m

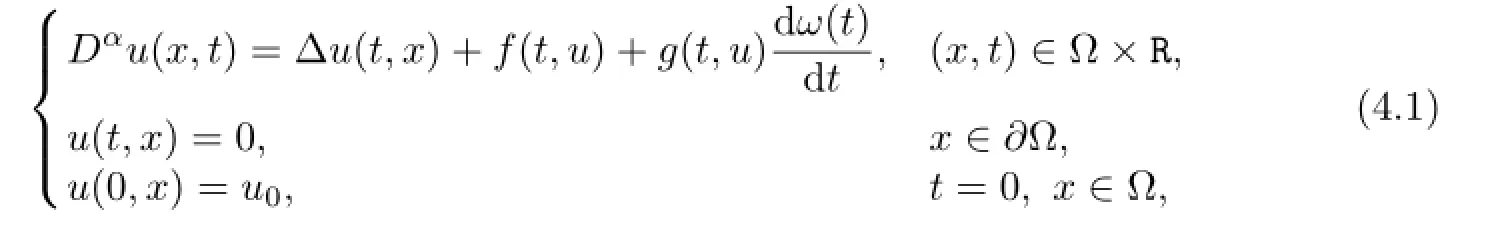
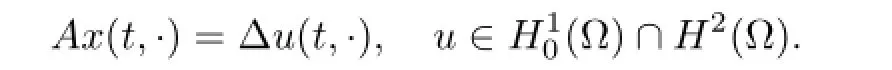
It is well known that(for example,see[17])Ais the infinitesimal generator of an analytic semigroupon satisfying(A1).Thus,if the conditions of Theorem 3.1 are satisfied,by applying Theorem 3.1,system(4.1)has a uniquepth moment almost periodic mild solution in fractional power spaceD((A)γ).Similarly,if the conditions of Theorem 3.2 are satisfi ed,by Theorem 3.2,system(4.1)has at least onepth moment almost periodic mild solution in fractional power spaceD((A)γ).

[1]A.A.Kilbas,H.M.Srivastava,J.J.Trujilio,Theory and Applications of Fractional Diff erential Equations,Elsevier,North-holiand,2006.

[2]J.Wang,Y.Zhou,Existence of mild solutions for fractional delay evolution systems,Applied MathematicsandComputation,218(2011),357-367.

[3]J.Cao,Q.Yang,Z.Huang,Existence of anti-periodic mild solutions for a class of semilinear fractional diff erential equations,CommunicationsinNonlinearScienceandNumerical Simulation,17(2012),277-283.

[4]Z.Wei,Q.Li,J.Che,Initial value problems for fractional diff erential equations involving Riemann-Liouville sequential fractional derivative,JournalofMathematicalAnalysisandApplications,367(2010),260-272.

[5]V.Lakshmikantham,A.S.Vatsala,Theory of fractional diff erential inequalities and applications,CommunicationsinAppliedAnalysis,11(2007),395-402.

[6]V.Lakshmikantham,A.S.Vatsala,Basic theory of fractional diff erential equations,Nonlinear Analysis:Theory,Methods&Applications,69(2008),2677-2682.

[7]V.Lakshmikantham,Theory of fractionalfunctional diff erentialequations,NonlinearAnalysis: Theory,Methods&Applications,69(2008),3337-3343.

[8]Y.Zhou,F.Jiao,J.Li,Existence and uniqueness for fractional neutral diff erential equations with infi nite delay,NonlinearAnalysis:Theory,Methods&Applications,71(2009),3249-3256.

[9]R.P.Agarwal,Y.Zhou,Y.He,Existence of fractionalneutral functional diff erential equations,Computers&MathematicswithApplications,59(2010),1095-1100.

[10]M.Benchohra,J.Henderson,S.K.Ntouyas,A.Ouahab,Existence results for fractional order functional diff erential equations with infinite delay,JournalofMathematicalAnalysisand Applications,338(2008),1340-1350.

[11]T.Jankowski,Fractional equations of Volterra type involving a Riemann-Liouville derivative,AppliedMathematicsLetters,26(2013),344-350.

[12]L.Arnold,C.Tudor,Stationary and almost periodic solutions of almost periodic affi ne stochastic diff erential equations,StochasticsandStochasticReports,64(1998),177-193.

[13]P.H.Bezandry,T.Diagana,Existence of almost periodic solutions to some stochastic diff erential equations,ApplicableAnalysis,86(2007),819-827.

[14]J.Cao,Q.Yang,Z.Huang,On almost periodic mild solutions for stochastic functional diff erential equations,NonlinearAnalysis:RealWorldApplications,13(2012),275-286.

[15]Z.Li,K.Liu,J.Luo,On almost periodic mild solutions for neutral stochastic evolution equations with infi nite delay,NonlinearAnalysis:Theory,Methods&Applications,110(2014),182-190.

[16]Y.Wang,Z.Liu,Almost periodic solutions for stochastic diff erentialequations with l´evy noise,Nonlinearity,25(2012),2803.

[17]A.Pazy,Semigroups of Linear Operators and Applications to Partial Diff erential Equations, Springer-Verlag,New York,1983.

[18]M.M.El-Borai,Some probability densities and fundamental solutions of fractional evolution equations,Chaos,Solitons&Fractals,14(2002),433-440.

[19]J.Cao,Q.Yang,Z.Huang,Optimal mild solutions and weighted pseudo-almost periodic classical solutions of fractionalintegro-diff erential equations,NonlinearAnalysis:Theory,Methods&Applications,74(2011),224-234.

[20]A.Ichikawa,Stability of semilinear stochastic evolution equations,JournalofMathematical AnalysisandApplications,90(1982),12-44.

(editedbyLiangweiHuang)

∗This work was partially supported by NSF of Jiangxi Province(Nos.20151BAB212011 and 20151BAB201021)and NNSF of China(No.11461044).

†Manuscript received December 21,2014

‡Corresponding author,E-mail:hongwei-yin@hotmail.com,yinhongwei@ncu.edu.cn