A NEW DISCRETE INTEGRABLE COUPLING SYSTEM AND ITS HAMILTONIAN STRUCTURE FOR THE MODIFIED TODA LATTICE HIERARCHY∗†

Shuo Feng,Fajun Yu

(SchoolofMath.andSystemScience,ShenyangNormalUniversity,Shenyang110034)

A NEW DISCRETE INTEGRABLE COUPLING SYSTEM AND ITS HAMILTONIAN STRUCTURE FOR THE MODIFIED TODA LATTICE HIERARCHY∗†

Shuo Feng,Fajun Yu‡

(SchoolofMath.andSystemScience,ShenyangNormalUniversity,Shenyang110034)

We present a new discrete integrable coupling system by using the matrix Lax pairU,V∈sl(4).A novel spectral problem of modifi ed Toda lattice soliton hierarchy is considered.Then,a new discrete integrable coupling equation hierarchy is obtained through the method of the enlarged Lax pair.Finally,we obtain the Hamiltonian structure of the integrable coupling system of the soliton equation hierarchy using the matrix-form trace identity.This discrete integrable coupling system includes a kind of a modified Toda lattice hierarchy.

integrable coupling system;modified Toda lattice hierarchy;Hamiltonian structure;enlarged Lax pair

2000MathematicsSubjectClassification47H30;34K30

1 Introduction

As is wellknown,in recent years there has been an explosion of interesting in the area of discrete integrable equations.Searching some new integrable lattice equations has become an significant and challenging topic,because new discrete integrable systems can be applied to many scientifi c areas,such as mathematical physics,quantum physics,statistical physics etc[1-4].

There have been many ways to construct the integrable couplings.In[5],Ma and Fuchssteiner first proposed perturbation method for establishing integrable couplings.Zhang Yufeng and Zhang Hongqing presented a method to construct integrable couplings with finite dimensionalmatrix Lie algebra in[6].Zhang,Xia and Fan presented the enlarged Lie algebra method to obtain integrable couplings in[6-12].Ma,Xu and Zhang once obtained a discrete integrable couplings through the semi-direct sums of Lie algebras[13].A beautiful method to generate Hamiltonian structures for integrable couplings associated with semi-direct sums of Lie algebras of the type was proposed in[14].

As we know,there have been few papers about the discrete integrable coupling system.

When studying a new discrete spectral problem coming,the way to construct the integrable equation is particularly important.In this work,we present a new discrete integrable coupling system by using the matrix Lax pairU,V∈sl(4),and obtain its Hamiltonian structure of the integrable coupling system of the soliton equation hierarchy,which includes a modified Toda lattice hierarchy.

2 The Modifi ed Toda Lattice Hierarchy and Its Hamiltonian Structure

The Tu method[15]for generating discrete integrable equation hierarchy and Hamiltonian system has huge infl uence longevity.Guo Fukui considered the sub-algebra of Loop algebra and constructed the Hamilton structure of integrable equation hierarchy in[16].In this paper,we consider the new discrete spectral problem by suing the mentioned method.

Eis a shift operator defined as follows:

whichn∈Z,t∈R.

And consider the following discrete spectral problem withg=sl(2,R)[17]:

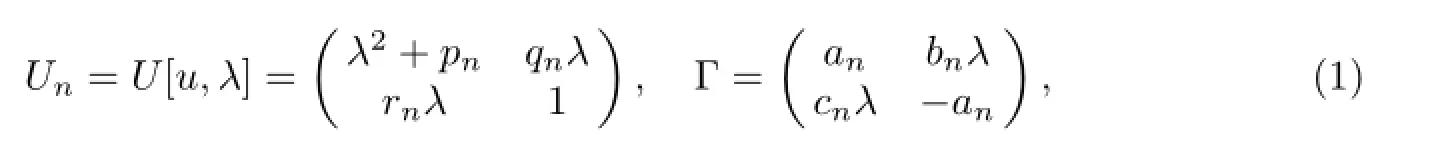
with the operation satisfying the following relations

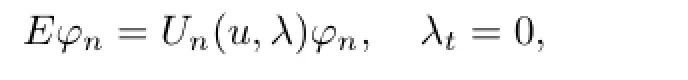
and

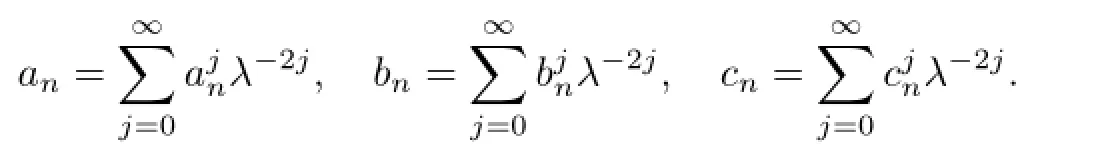
We defi ne the subalgebra of loop algebra esl(2)as

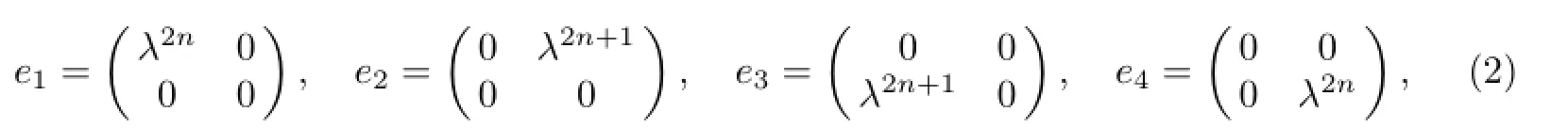
and get the following form of discrete Lax pair

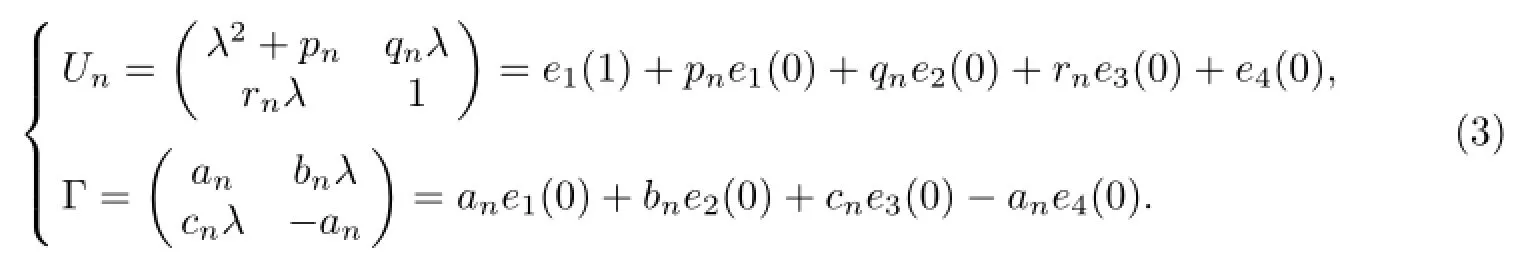
Solving the stationary discrete zero curvature equation(EΓ)Un-UnΓ=0,we acquire the system as follows

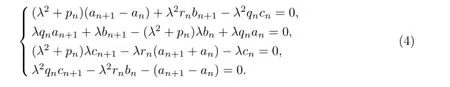
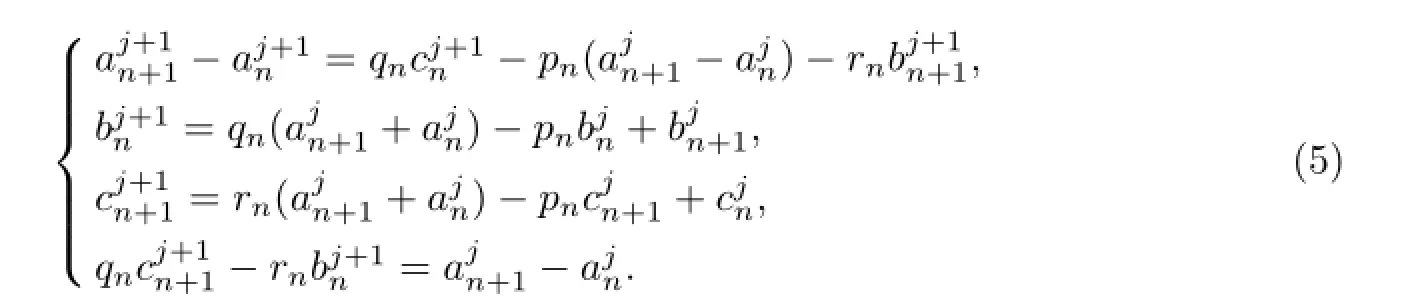
According to the above equations,we can obtain

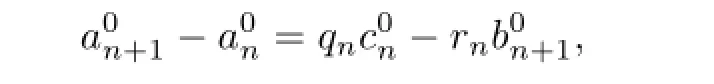
where the initial values

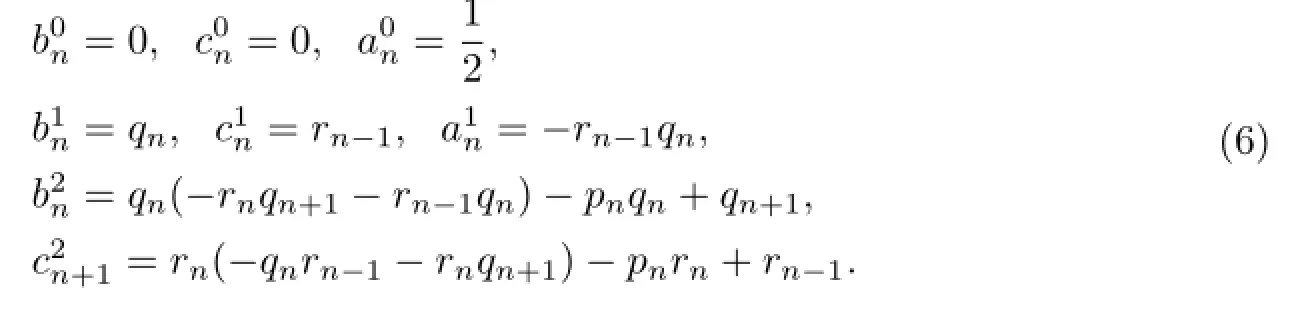
From(5),the recursive operatorLis given as follows

with

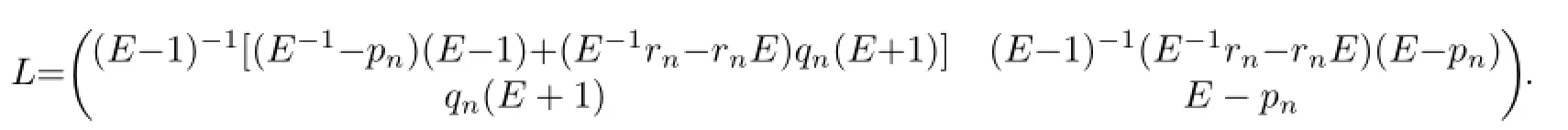
Note that the conditions

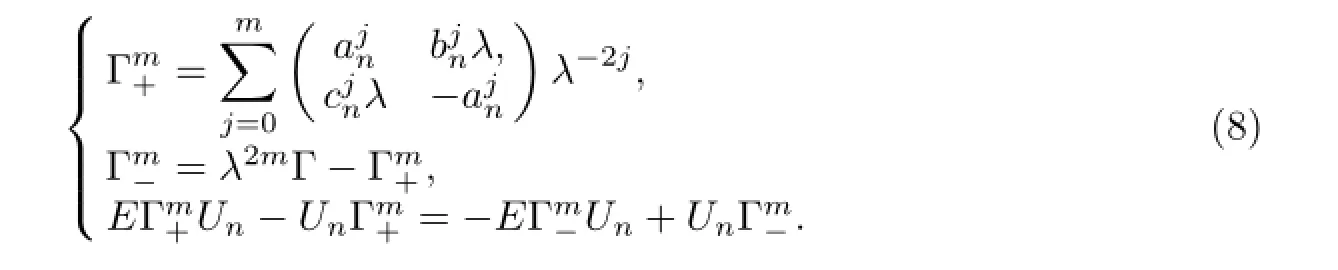
According to the stationary discrete zero curvature equation,we have

Choosing the correction term

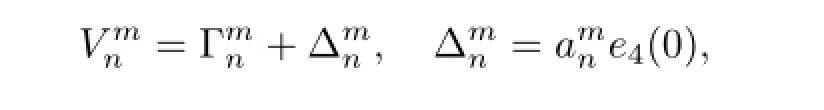
we obtain

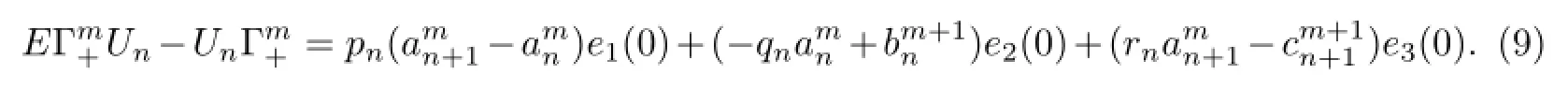
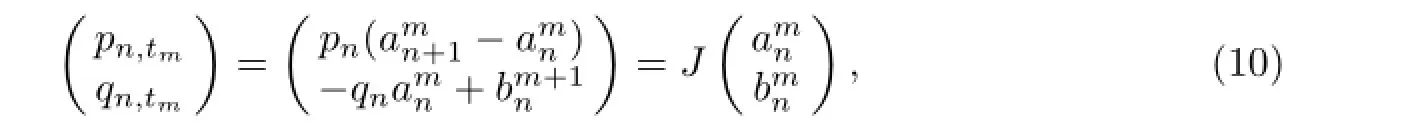
and

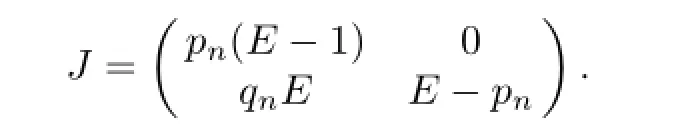
Whenm=1,the first equations can rewritten

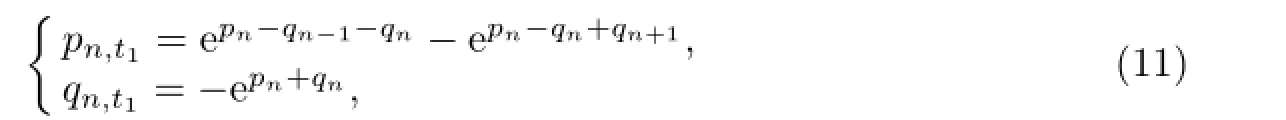
which has the similar structure of the Toda lattice equation,so we generalize the modifi ed Toda lattice hierarchy.

By using of Tu method,to obtain its Hamiltonian structure,we introduceto calculate the discrete trace identity

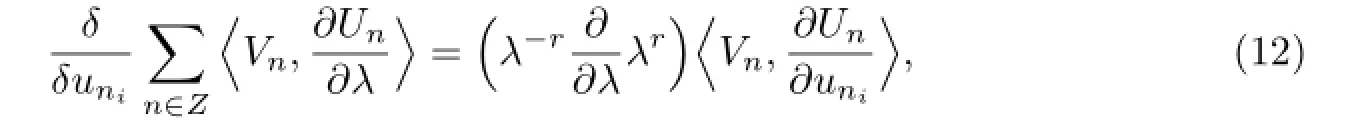
then we have

and

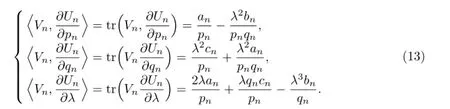
Substituting the above formulas into(12),we can obtain the following discrete hierarchy

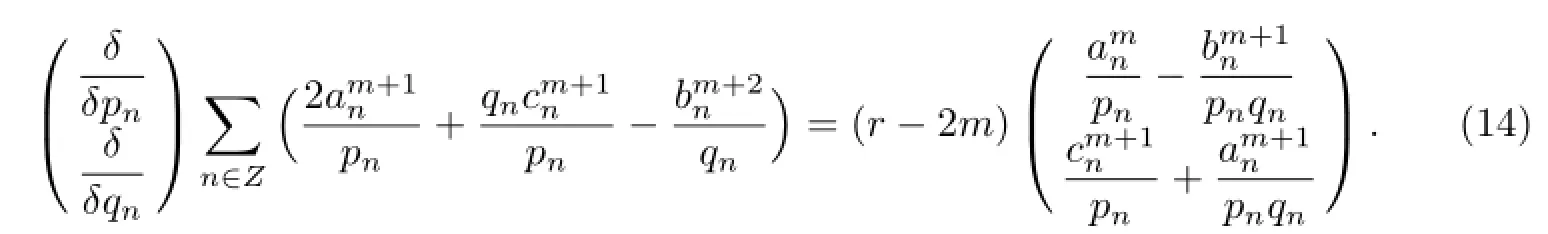
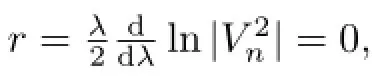
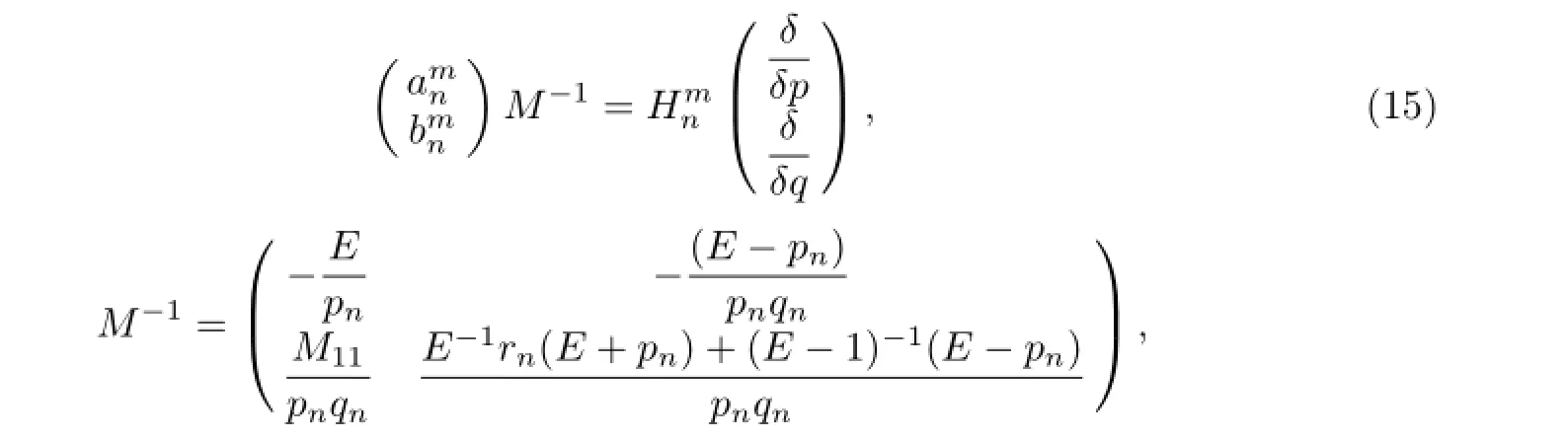
with

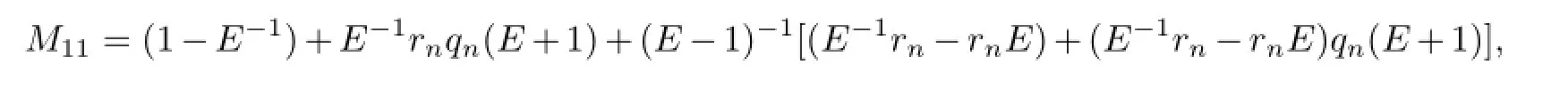
and Hamiltonian structure

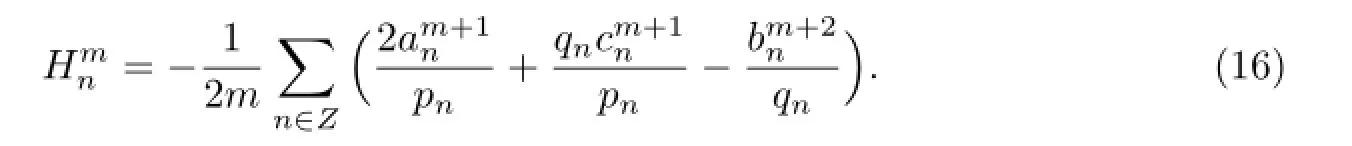
By using of Tu method,the discrete zero equation admits the nonlinear modifi ed Toda lattice hierarchy

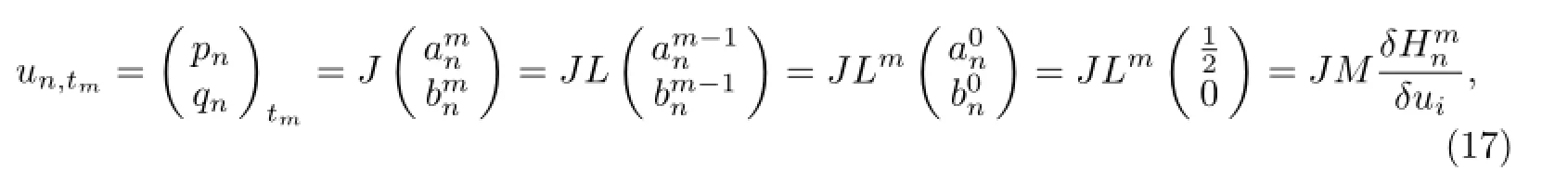
and the recursive operatorLand the operatorsJ,Mcome from equations(7),(10)and (15).

3 The Integrable Coupling System and Its Hamiltonian Structure

Consider the discrete zero curvature equation

which is equivalent to the following equation

or

Substituting equation(18)into(19)gives rise to

Setting

we obtain an extended recurrence relation from equation(21)

and

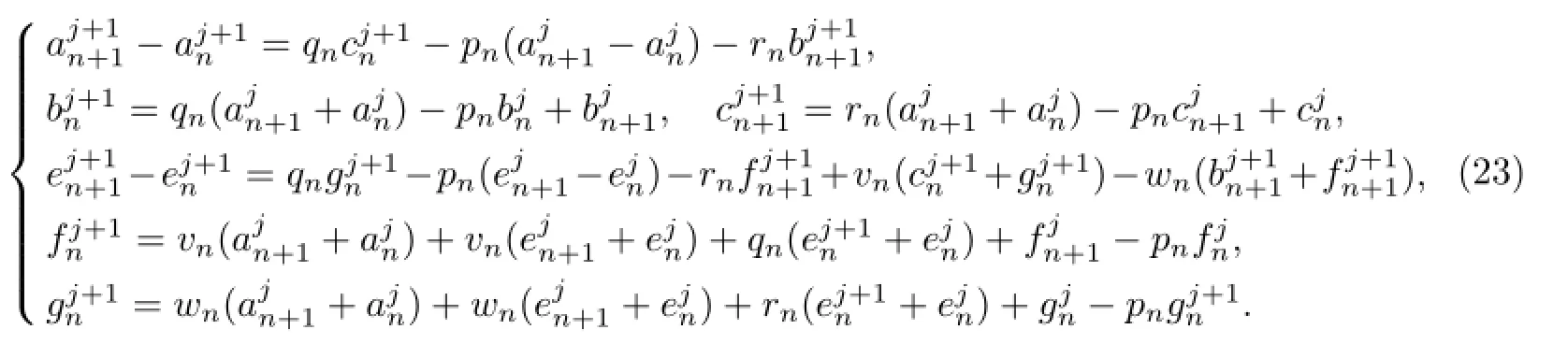
On the initial value,we take the terms as follows

According to(23),we derive

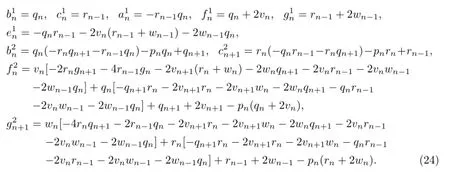
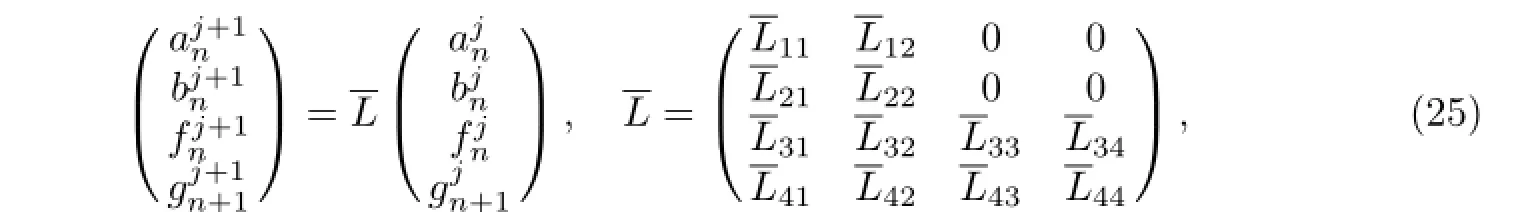
with

In order to search for the discrete integrable equation hierarchy,we consider

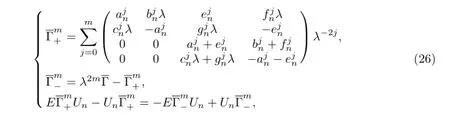
then we obtain the following equation through copulating the degree ofλ

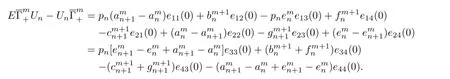
Next we want to construct the integrable coupling system of the modifi ed Toda lattice hierarchy.Taking the correction term as follows

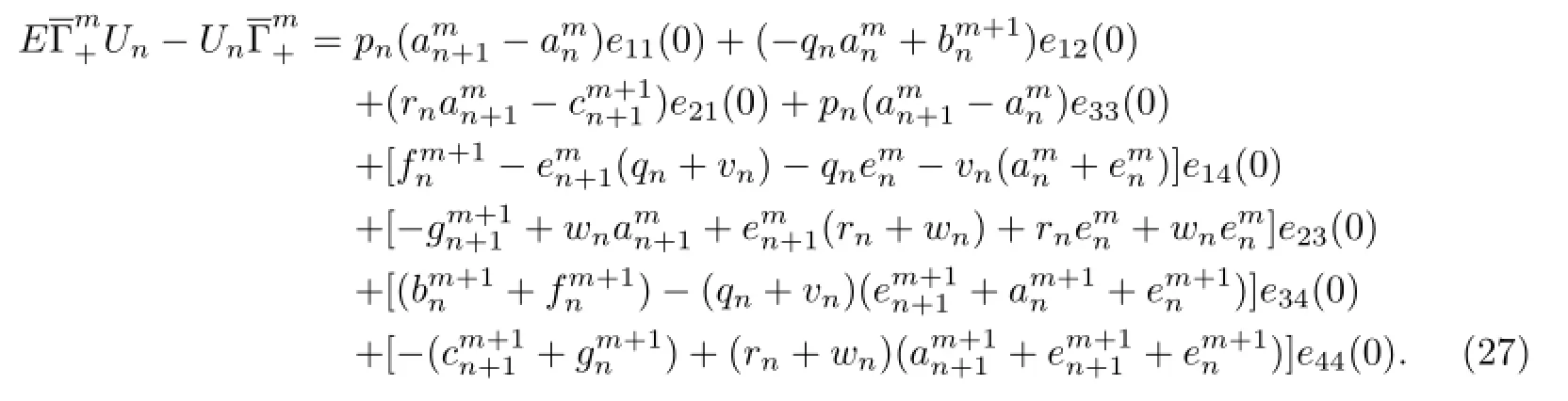
By using of Tu method,the discrete zero curvature equation admits the following lattice soliton equation hierarchy:

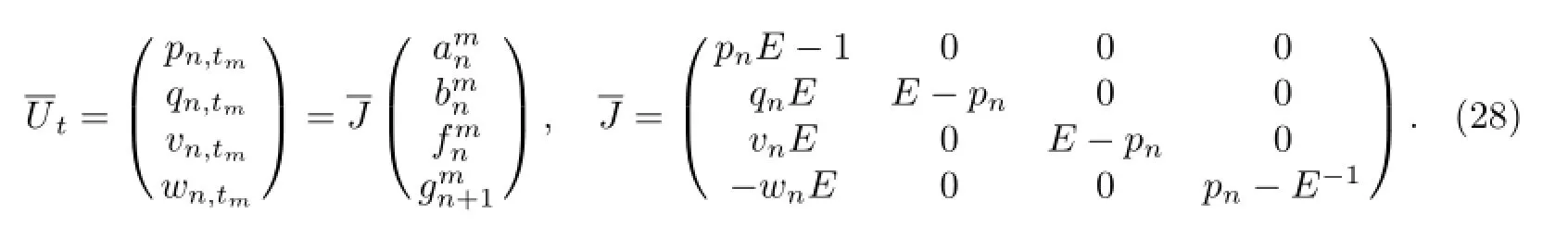
We obtain the discrete integrable coupling system of the new lattice soliton equation (28).Whenvn=wn=0,we obtain the known lattice soliton equation hierarchy(10). It is generalized Toda lattice soliton equation,which is one of fundamental equations in mathematics physics.

Next,we shallconstruct the corresponding Hamiltonian structure ofthe integrable coupling hierarchy(28)by the discrete variational identity[21]

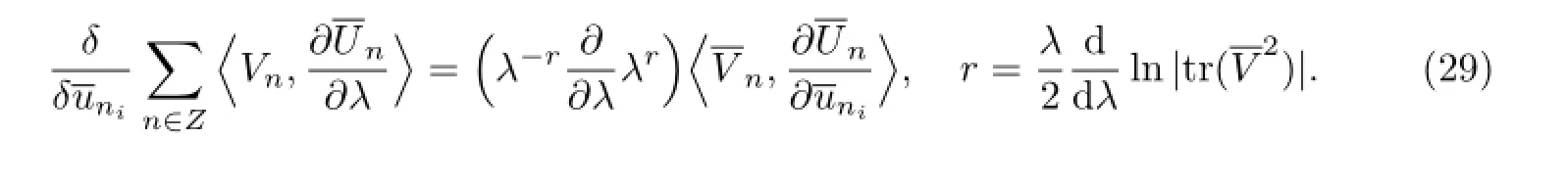
The operation relations are defi ned as follows

In terms ofFwe can obtain the symmetric matrix

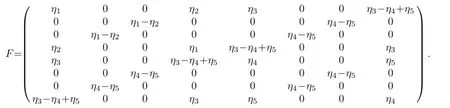
Thus,a direct calculation gives

According to the discrete trace identity(29),the coupling Hamiltonian structure is presented as follows

which gives rise to

We get the Hamiltonian function

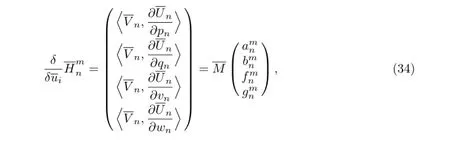
where

and

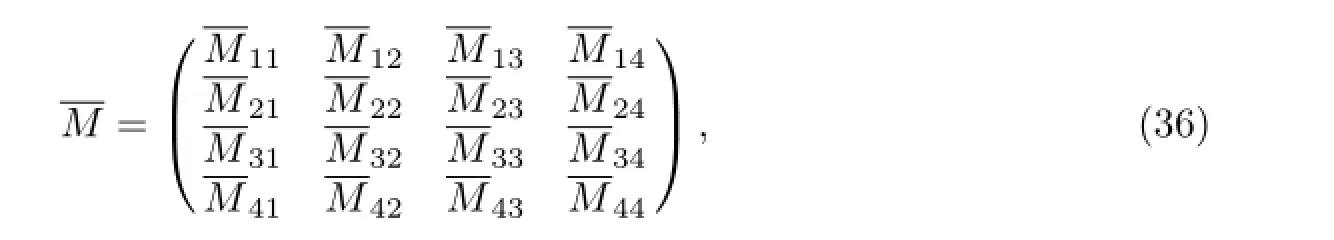
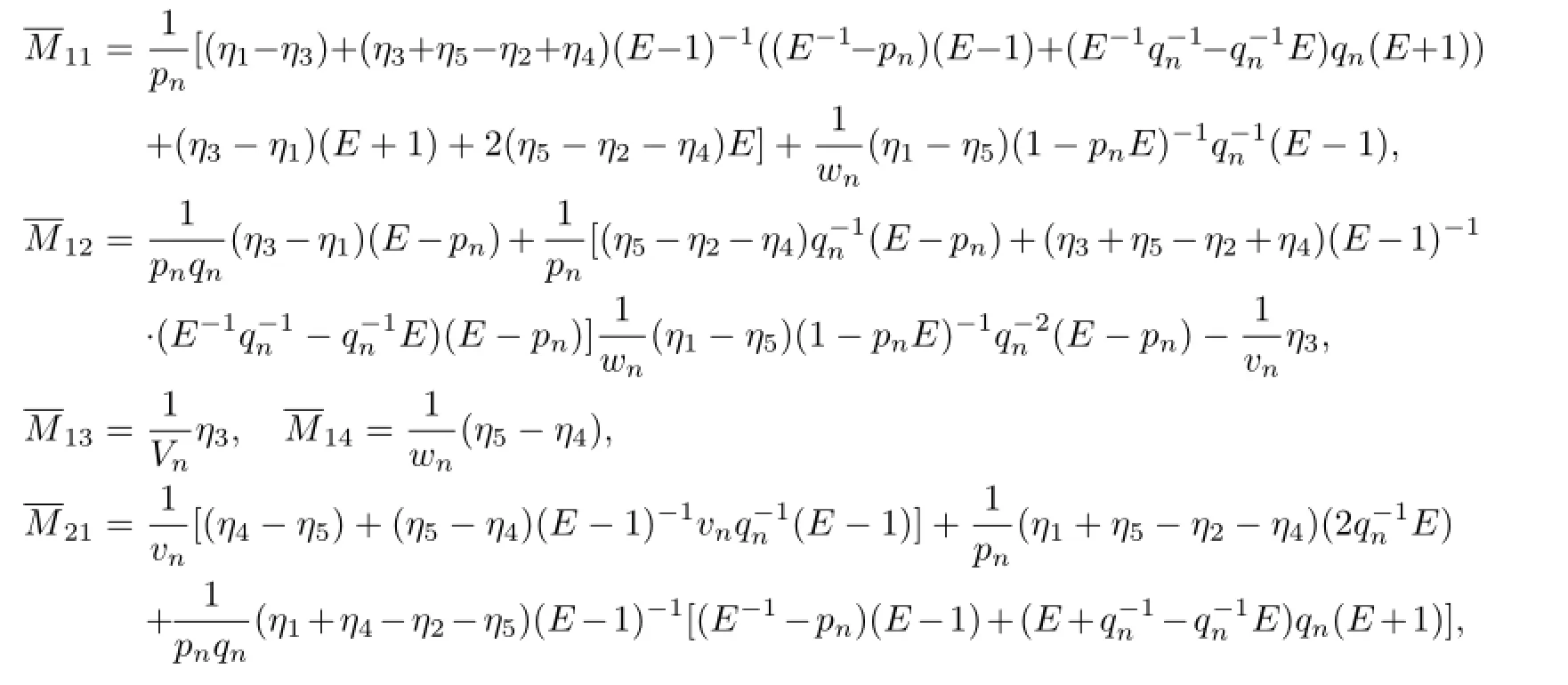
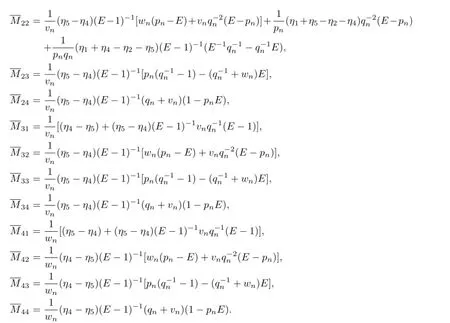
A bi-Hamiltonian structure of the discrete integrable coupling hierarchy(28)is derived using the discrete zero curvature equation

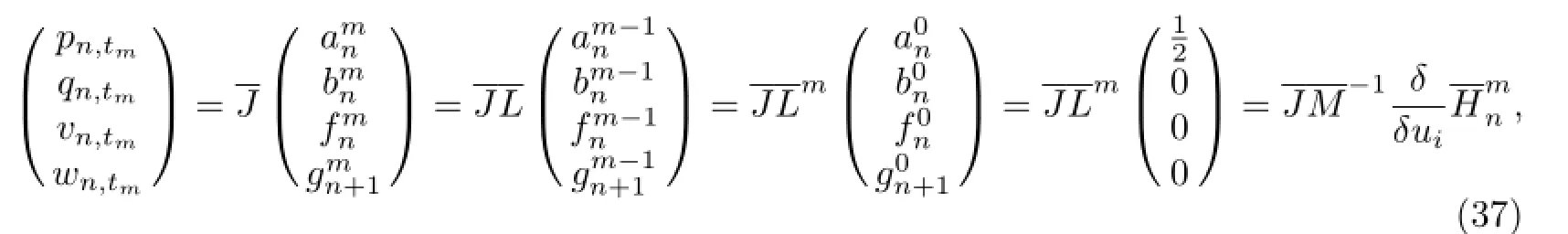
We obtain the integrable coupling system of the modified Toda lattice hierarchy by using of matrix Lie algebrasl(4),and obtain its Hamiltonian structure through the discrete trace identity.Whenvn=w2n=0,it is the known modified Toda lattice hierarchy.So system (37)is a novel discrete soliton equation hierarchy.The previous papers were not designed for constructing the integrable coupling equations hierarchy and its Hamiltonian structure, thus our results are interesting.

4 Conclusions

In this paper,we obtain the new discrete soliton equation integrable coupling by using the matrix Lie algebrasl(4).The discrete integrable coupling system can be simplifi ed to the modifi ed Toda lattice hierarchy,and the corresponding Hamiltonian structure of thecoupling equation hierarchy is obtained by the discrete variational trace identity.Moreover, the discrete integrable couplings of construction method can be applied to generate other discrete soliton equations integrable coupling systems.The general idea in our analysis could also be applied to higher-dimensional soliton equations.There are some worthwhile problems can be studied in the future.

[1]M.Blaszak and K.Marciniak,R-matrix approach to lattice integrable systems,J.Math.Phys.,35(1994),4661-4682.

[2]P.R.Gordoa,N.Joshi and A.Pickering,On a Generalized 2+1 Dispersive Water Wave Hierarchy,Publ.RIMS(Kyoto),37(2001),327-347.

[3]C.H.Gu,Y.S.Li,G.Z.Tu,Soliton Theory and Its Application,Hangzhou:Zhejiang Publishing House of Science and Technology,1990.

[4]B.Fuchssteiner,Coupling of Completely Integrable Systems,Dordrecht:Kluwer,1993,p125.

[5]W.X.Ma and B.Fuchssteiner,Integrable theory of the perturbation equations,Chaos,Solitons Fractals,7(1996),1227-1250.

[6]Y.F.Zhang and H.Q.Zhang,A direct method for integrable couplings of TD hierarchy,J. Math.Phys.,43(2002),466-472.

[7]Y.F.Zhang,E.G.Fan and Y.Q.Zhang,Discrete integrable couplings associated with Toda-type lattice and two hierarchies of discrete soliton equations,Phys.Lett.A,357(2006),454-461.

[8]T.C.Xia,F.C.You and D.Y.Chen,A generalized cubic Volterra lattice hierarchy and its integrable couplings system,Chaos,SolitonsFractals,27(2006),153-158.

[9]E.G.Fan,A diff erential-diff erence hierarchy associated with relativistic Toda and Volterra hierarchies,Phys.Lett.A,372(2008),6368-6374.

[10]E.G.Fan and H.H.Dai,A diff erential-diff erence hierarchy associated with relativistic Toda and Volterra hierarchies,Phys.Lett.A,372(2008),4578-4585.

[11]F.J.Yu,A non-isospectralintegrable couplings of Volterra lattice hierarchy with self-consistent sources,Appl.Math.Comp.,215(2009),1217-1223.

[12]F.J.Yu and L.Li,A new method to construct the integrable coupling system for discrete soliton equation with the Kronecker product,Phys.Lett.A,372(2008),3548-3554.

[13]W.X.Ma,X.X.Xu and Y.F.Zhang,Semidirect sums of Lie algebras and discrete integrable couplings,J.Math.Phys.,47(2006),053501.

[14]W.X.Ma and M.Chen,Hamiltonian and quasi-Hamiltonian structures associated with semidirect sums of Lie algebras,J.Phys.A:Gen.Math.,39(2006),10787-10801.

[15]G.Z.Tu,A trace identity and its applications to the theory of discrete integrable systems,J. Phvs.A:Math.Gen.,23(1990),3903-3922.

[16]F.K.Guo,Subalgebra eA1of Loop algebra and integrable Hamilton equation hierarchy,Acta MathematicaScientia,19(1999),507-512.

[17]X.H.Chen and H.Q.Zhang,Two new discrete integrable systems,Chin.Phys.B,22(2013),030203.

[18]W.X.Ma,A bi-Hamiltonian formulation for triangular systems by perturbations,J.Math. Phys.,43(2002),1408-1421.

[19]W.X.Ma,Enlarging spectral problems to construct integrable couplings of soliton equations,Phys.Lett.A,316(2003),72-76.

[20]W.X.Ma,Integrable couplings and matrix loop algebra,in:Nonlinear and Modern Mathematical Physics,pp.105-122,edited by W.X.Ma and D.Kaup,AIP Conference Proceedings, Vol.1562(American Institute of Physics,Melville,NY,2013).

[21]W.X.Ma,A discrete variationalidentity on semi-direct sums of Lie algebras,J.Phvs.A:Math. Gen.,40(2007),15055-15069.

(editedbyLiangweiHuang)

∗This work was supported by the Natural Science Foundation of Liaoning Province Grant No.2013020056.

†Manuscript received April 20,2015;Revised May 21,2015

‡Corresponding author.E-mail:yufajun888@163.com