A HOMOTOPY-BASED ALTERNATING DIRECTION METHOD OF MULTIPLIERS FOR STRUCTURED CONVEX OPTIMIZATION∗†

Yiqing Dai,Zheng Peng

(CollegeofMath.andComputerScience,FuzhouUniversity,Fuzhou350116)

A HOMOTOPY-BASED ALTERNATING DIRECTION METHOD OF MULTIPLIERS FOR STRUCTURED CONVEX OPTIMIZATION∗†

Yiqing Dai,Zheng Peng‡

(CollegeofMath.andComputerScience,FuzhouUniversity,Fuzhou350116)

The alternating direction method of multipliers(ADMM for short)is effi cient for linearly constrained convex optimization problem.The practical computational cost of ADMM depends on the sub-problem solvers.The proximal point algorithm is a common sub-problem-solver.However,the proximal parameter is sensitive in the proximal ADMM.In this paper,we propose a homotopy-based proximal linearized ADMM,in which a homotopy method is used to solve the sub-problems at each iteration.Under some suitable conditions,the globalconvergence and the convergence rate ofO(1/k)in the worst case of the proposed method are proven.Some preliminary numerical results indicate the validity of the proposed method.

separable convex optimization;alternating direction method of multipliers,proximal point method;homotopy method

2000MathematicsSubjectClassification47N10

1 Introduction

In this paper,we consider a structured convex optimization problem of the form:

whereandθ2:Rn2→Rare closed convex functions,.BothAandBare orthogonal matrices,which means thatWe assume that the solution set of problem(1),denoted byΩ∗,is nonempty.Unless otherwise stated,‖·‖representsF-norm(for matrix);‖·‖representsE-norm(for vector).

In recent years,the structured convex optimization problem has become a research focus since it has been applied in many fi elds,such as compressed sensing[1],large-scale linear algebraic equations problem[2],image processing[3,4],statistical problem[5],etc.The alternating direction method of multipliers(ADMM)is effi cient for this kind of problems. ADMMwas first proposed by[6].It has drawn many authors’attention,thus various effi cientvariants of ADMM have been developed,see[7-9].[10-12]paid much attention in ADMM and got excellent achievements.The practical computational cost of ADMM depends on the sub-problem solvers,and many researchers have proposed various sub-problem-solvers. For example,Ye and Yuan[13]proposed a prediction-correction ADMM for structured monotone variation inequalities,He,Liao and Qian[10]suggested linearizing the quadratic terms of the objective function before the iteration.The proximal point algorithm is a common subproblem-solver.However,in the proximal ADMM,the proximal parameter is sensitive.In order to overcome this shortcoming and accelerate ADMM,we propose a homotopy-based proximal linearized ADMM,in which a homotopy method is used to solve the iteration sub-problem.

The homotopy method was first known in 1930s,which was a powerfultool for nonlinear problem[14,15],and it has scored tremendous achievements in both convex and nonconvex programming[15].The continuous homotopy method was developed in 1970s,which has the feature of global convergence.Chow[16]proposed Chow-York algorithm,Watson[17] developed a numericalalgorithm to solve nonlinear complementarity problem[18]and nonlinear two-point boundary value problem[19].Recently,Li and Lin[20]designed a homotopy method for variational inequality problem in both bound set and unbound set.Li,Yu and Xu[21]proposed a constrain shifting homotopy method(CSHM)for solving nonlinear programming with both equality and inequality constraints.Other applications of homotopy methods are referred to[22-24].

The idea of homotopy method is to continuously transform a simple problem into the given hard problem[14].The original problemf(x)=0 is hard,but the problemx-a=0 is easy.We defi ne a homotopy mapping as follows

where 0≤λ≤1.We can obtain a series solution ofH(x,λ)=0 by changing the parameterλfrom zero to one.Ifλ=0,the solution of functionH(x,0)=0 is equal to that of the simple problemx-a=0.Ifλ=1,the solution ofH(x,1)=0 is what we want.

In this paper,a homotopy-based proximallinearized ADMM for solving problem(1.1)is constructed.Under some suitable assumptions,the global convergence and the convergence rate ofO(1/k)in the worst case are proven,the validity of the proposed method is shown by some numerical tests.

The paper is organized as follows:Section 2 contains some preliminaries,in which the proximal linearized ADMM and some useful properties are described.Section 3 presents the homotopy-based proximal linearized ADMM.In Section 4,we prove the convergence property of the proposed method.In Section 5,the convergence rate ofO(1/k)in the worst case is investigated.Some numericalresults are provided to show the validity ofthe proposed method is Section 6.Finally,we give some concluding remarks.

2 Preliminaries

In this section,we fi rst recall the fi rst-order optimality conditions for problem(1.1),and the proximal linearized ADMM in[10,25].

Letλ∈Rmbe the Lagrangian multiplier associated to the linear constraint in(1.1). For convenience,we assume that bothθ1(x)andθ2(y)are diff erentiable.By the fi rst-orderoptimality conditions,solving problem(1.1)is to find a triple(x∗,y∗,λ∗)such that

ADMM is a simple but powerful algorithm which is well suited to convex optimization [26].At each iteration,ADMM produces the new iterate(),from a given (xk,yk,λk),via the following scheme:

(S1)Given(yk,λk),xk+1is a solution of the following problem

(S2)Fixedxk+1andλk,yk+1is a solution of the following problem

(S3)The Lagrange multiplierλis updated by:

By simplifying the sub-problems(2.2)and(2.3),[10]and[25]proposed the proximal linearized ADMM.Problems(2.2)and(2.3)can be respectively written as:

Linearizing the quadratic terms of(2.5)and(2.6)atxkandyk,and adding the proximal termsandrespectively,we get

and

3 The Proposed Method

In fact,problems(2.7)and(2.8)are respectively equivalent to

and

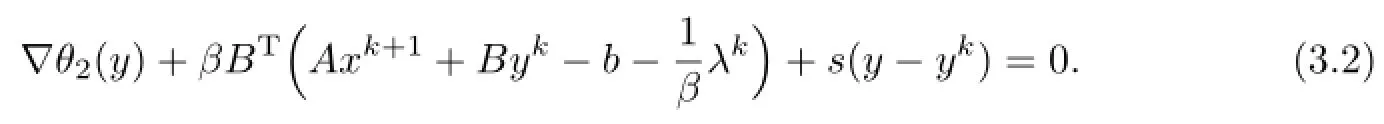
They can be further respectively written as

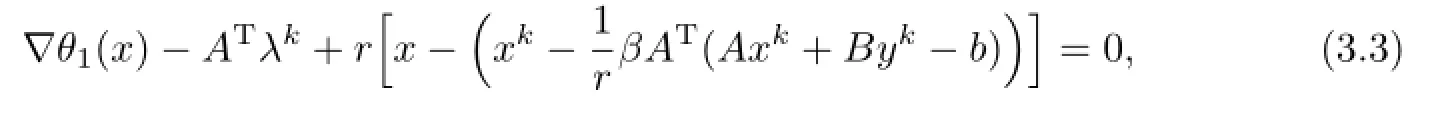
and

We are now at the position to propose the homotopy-based proximal linearized ADMM as follows.

Algorithm3.1Homotopy-based Proximal Linearized Alternating Direction Method of Multipliers(HomPLADMM)

(s1)Letxk+1be a solution of

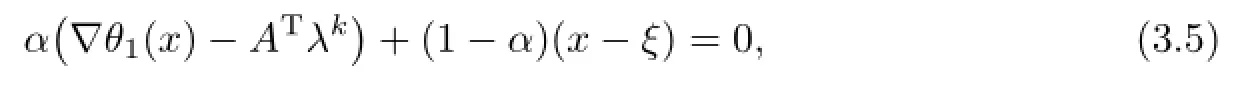
(s2)Letyk+1be a solution of

(s3)Update Lagrangian multiplier by

Remark3.1In the implementation,both subproblems(3.5)and(3.6)can be solved by the preconditioned conjugate gradient method proposed by Pytlak and Tarnawski[27].

Sincexk+1is the solution of(3.5),we have

Similarly,

By(2.4)and(3.7),(3.8),we get

and

In fact,(2.4)can be written as

Equations(3.9)-(3.11)can be rewritten as the following compact form:

where

4 Convergence Analysis

In this section,we prove the convergence property of Algorithm 3.1.

Lemma4.1LetbegeneratedbyAlgorithm3.1forgiven

ProofBy(3.12),we have

By the convexity ofθ1andθ2,we get the monotonicity ofF,thus

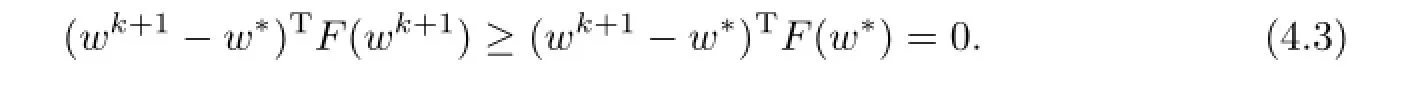
On the other hand,from(4.2),we obtain

It follows from(4.4),(4.2)and(4.3)that,we have

Lemma4.2Letwk+1=(xk+1,yk+1,λk+1)begeneratedbyAlgorithm3.1foragiven wk=(xk,yk,λk),thenwehave

whereN=sIn2-βBTB.

ProofEquation(3.10)can be reformed as:

At thek-th iteration,it has

Combining(4.6)with(4.7),we obtain

which implies

By(4.8),we have:

Because the fact thatθ2(y)is a convex function,and∇θ2(y)is a monotone operator,we have

Substituting(4.10)and(4.11)into(4.9),we obtain

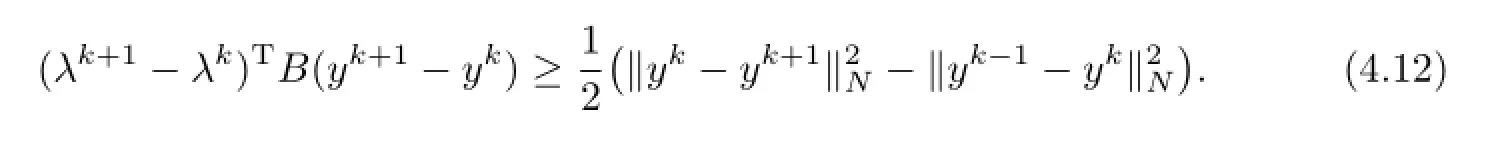
Lemma4.3Letwk+1=(xk+1,yk+1,λk+1)begeneratedbyAlgorithm3.1forgiven vectorwk=(xk,yk,λk)andw∗=(x∗,y∗,λ∗)∈Ω∗,thenwehave

ProofBy a directly computation,we have

It follows from Lemmas 4.1 and 4.2 that

Substituting(4.15)into(4.14),we get

This is the desired inequality.

Theorem4.1Thesequence{wk}generatedbyAlgorithm3.1convergestow∞,which isasolutionofproblem(1.1).

ProofBy the assumption,‖ATA‖=‖BTB‖=1,using the relation ofα,β,rands, we have:r＞β=β‖ATA‖ands＞β=β‖BTB‖.It is easy to check thatPandNare both symmetric and positive definite matrices.It follows from Lemma 4.3 that

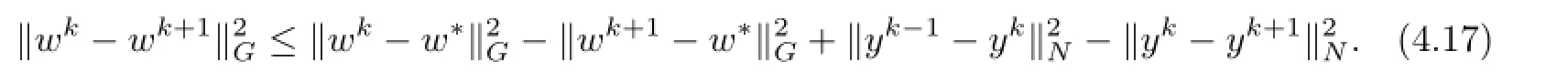
Summing inequality(4.17)fromk=1 to∞,we get

Hence,

The termination criteria maxprovides that the proposed method will stop in fi nite iterations for a givenε＞0.It follows from(3.9)-(3.11) and(4.20)that

which implies thatw∞is a solution of problem(1.1).

5 Convergence Rate

In this section,inspired by[28-30],we establish a worst-caseO(1/k)convergence rate in the non-ergodic sense for the sequence{wk}generated by Algorithm 3.1.

For convenience,we introduce the following matrices

We also defi ne a new sequenceof the form

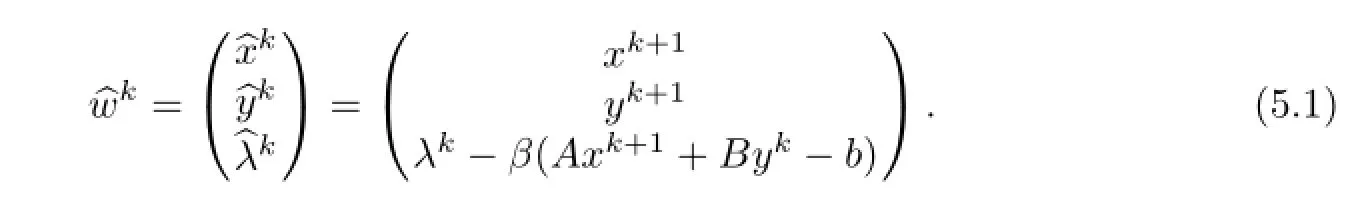
Then we have

Lemma5.1Let{bwk}bedefinedby(5.1),then

ProofBy(5.1),equations(3.9),(3.10)and(3.11)can be rewritten as

Hence

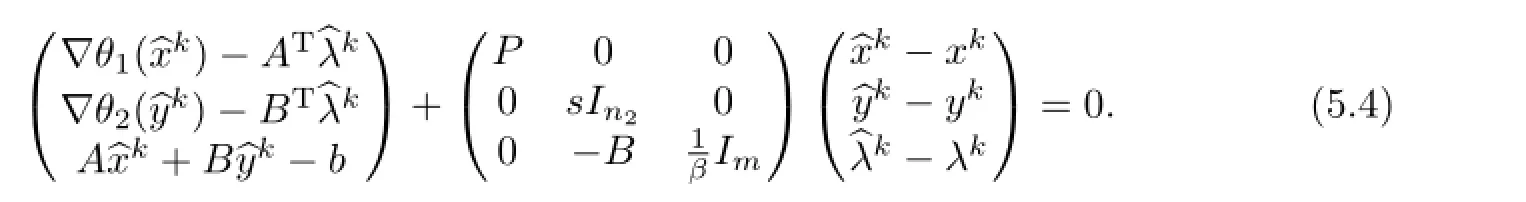
Lemma5.2Let{bwk}bedefinedby(5.1),where{wk}isgeneratedbyAlgorithm3.1, thenwehave

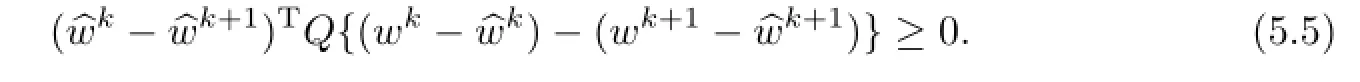
ProofBy Lemma 5.1,we have

Combining(5.2)and(5.6),we get

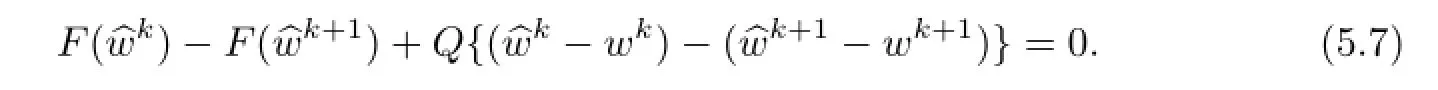
Multiplying both sides of(5.7)by the termwe have

The last inequality follows from the monotonicity of the operatorF.

Lemma5.3[28]Let{bwk}bedefinedby(5.1)and{wk}begeneratedbyAlgorithm3.1, thenweobtain

Lemma5.4Ifr＞β‖ATA‖ands＞β‖BTB‖,then

ProofBy a directly computation,we have

and

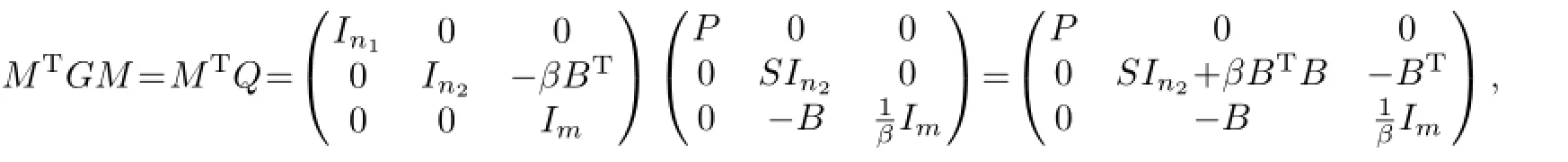
then

The last inequality follows from the fact thatr＞β‖ATA‖ands＞β‖BTB‖.

Lemma5.5[28](5.1),where{wk}isgeneratedbyAlgorithm3.1.Then,foranyk≥1wehave

Theorem5.1Let{wk}begeneratedbyAlgorithm3.1.Then,thereexistsaconstant d＞0suchthatforarbitrarilygivenε＞0,itattains

ProofBy(4.18)we have

By Lemma 5.5,the sequenceis monotonically non-increasing.Thus,

which implies

Theorem 5.1 establishes a worst-caseO(1/k)convergence rate of Algorithm 3.1 in the non-ergodic sense.

6 Numerical Experiments

In the section,we test Algorithm 3.1 by the correlation matrices calibrating problem. The codes of the method implemented in this section are written in Matlab and all experiments are performed in Matlab 2010b on a Lenovo personal computer with Intel Core(TM) i3 CPU 2.27GHz and 2G memory.

The test problem is used by Tao,Yuan and He[31],which can be formulated as

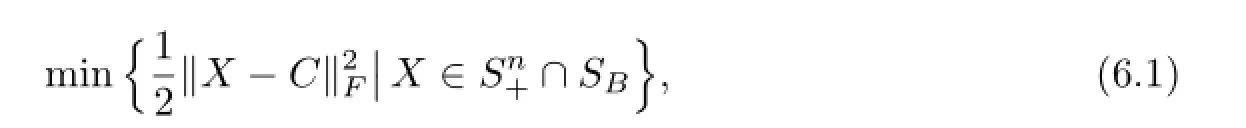
Problem(6.1)can be converted to the following separable form

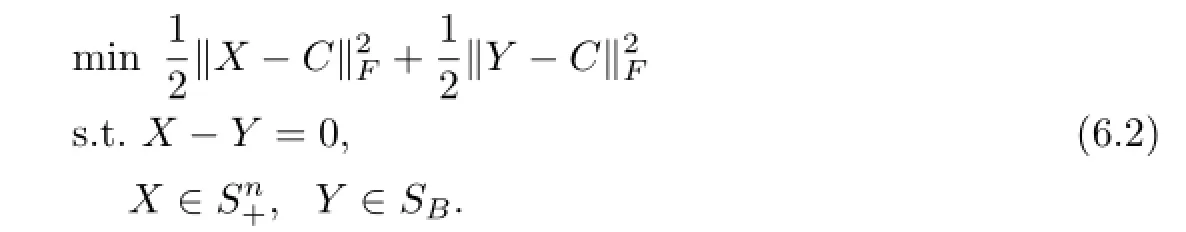
We set

as the initial point,and terminates Algorithm 3.1 whenever

whereε=10-3.In addition,we choose the penalty parameterβ=1.8,initialize the homotopy parameterα=10-2,and set

In the test problem,the matrixCis

and the matricesHLandHUare

and

We compare the proposed HomPLADMM in this paper,with the classical alternating direction method and the Glowinski alternating direction method.For each fi xedn,we test 50 problems generated byC=rand(n,n).The test results of the mentioned three methods in the terms of matrix dimensionn,average iterationsiter,average cpu timecputand average errorerrorare put into Table 6.1.

Table6.1Numerical results on problem(6.1)(cput in seconds)

7 Conclusion

In order to accelerate ADMM,we propose a homotopy-based proximallinearized ADMM, in which a homotopy idea is used to solve the sub-problem at each iteration.The convergence ofthe proposed algorithm is proven in this paper,and a worst-caseO(1/k)convergence rate(in the non-ergodic sense)of the sequence{wk}generated by the proposed method is established.Finally,some preliminary numericalresults are provided to indicate the validity of the proposed method.

[1]J.F.Yang and Y.Zhang,Alternating direction algorithms forℓ1-problems in compressive sensing,SIAMJournalonScientificComputing,33:1(2011),250-278.

[2]Z.Peng and D.H.Wu,An inexact parallel splitting augmented Lagrangian method for large system of linear equations,AppliedMathematicsandComputation,216:5(2010),1624-1636.

[3]Y.L.Wang,J.F.Yang,W.T.Yin and Y.Zhang,A new alternating minimization algorithm for total variation image reconstruction,SIAMJournalonImagingSciences,1:3(2008),248-272.

[4]J.F.Yang,Y.Zhang and W.T.Yin,An effi cient TVL1 algorithm for deblurring multichannel images corrupted by impulsive noise,SIAMJournalonScientificComputing,31:4(2009),2842-2865.

[5]X.M.Yuan,Alternating direction methods for sparse covariance selection,http://www. optimization-online.org/DBFILE/2009/09/2390.pdf.

[6]D.Gabay and B.Mercier,A dual algorithm for the solution of nonlinear variational problems via fi nite element approximation,ComputersandMathematicswithApplications,2:1(1976),17-40.

[7]M.Fukushima,Application of the alternating direction method of multipliers to separable convex programming problems,Computationaloptimizationandapplications,1:1(1992),93-111.

[8]J.N.Tsitsiklis,D.Bertsekas,Paralleland Distributed Computation:Numerical Methods,Prentice Hall,1989.

[9]S.Kontogiorgis and R.R.Meyer,A variable-penalty alternating directions method for convex optimization,MathematicalProgramming,83:1(1998),29-53.

[10]B.S.He,L.Z.Liao and M.J.Qian,Alternating projection based prediction-correction methods for structured variational inequalities,JournalofComputationalMathematics,24:6(2006),693-710.

[11]B.S.He,L.Z.Liao,D.Han and H.Yang,A new inexact alternating directions method for monotone variational inequalities,MathematicalProgramming,92:1(2002),103-118.

[12]B.S.He,M.H.Xu and X.M.Yuan,Solving large-scale least squares semidefnite programming by alternating direction methods,SIAMJournalonMatrixAnalysisandApplications,32:1(2011),136-152.

[13]C.H.Ye and X.M.Yuan,A descent method for structured monotone variational inequalities,OptimizationMethodsandSoftware,22:2(2007),329-338.

[14]L.T.Watson and R.T.Haftka,Modern homotopy methods in optimization,ComputerMethods inAppliedMechanicsandEngineering,74:3(1989),289-305.

[15]L.T.Watson,Theory of globally convergent probability-one homotopies for nonlinear programming,SIAMJournalonOptimization,11:3(2001),761-780.

[16]S.N.Chow,Finding zeroes of maps:homotopy methods that are constructive with probability one,MathematicsofComputation,32:143(1978),887-899.

[17]L.T.Watson,A globally convergent algorithm for computing fixed points ofc2maps,Applied MathematicsandComputtation,5:4(1979),297-311.

[18]L.T.Watson,Solving the nonlinear complementarity problem by a homotopy method,SIAM JournalonControlandOptimization,17:1(1979),36-46.

[19]C.Y.Wang and L.T.Watson,Squeezing of a viscous fuid between elliptic plates,FlowTurbulenceandCombustion,35:2-3(1979),195-207.

[20]Z.Lin and Y.Li,Homotopy method for solving variationalinequalities,JournalofOptimization TheoryandApplications,100:1(1999),207-218.

[21]Y.Li,B.Yu and Q.Xu,A constraint shifting homotopy method for general non-linear programming,Optimization,63:4(2014),585-600.

[22]Z.Lin,Y.Li and B.Yu,A combined homotopy interior point method for general nonlinear programming problems,AppliedMathematicsandComputation,80:2(1996),209-224.

[23]Z.H.Lin,B.Yu and G.C.Feng,A combined homotopy interior point method for convex nonlinear programming,AppliedMathematicsandComputation,84:2(1997),193-211.

[24]B.Yu,Q.H.Liu and G.C.Feng,A combined homotopy interior point method for nonconvex programming with pseudo cone condition,NortheasternMathematicalJournal,16:4(2000),383-386.

[25]M.H.Xu and T.Wu,A class of linearized proximal alternating direction methods,Journalof OptimizationTheoryandApplications,151:2(2011),:321-337.

[26]S.Boyd,N.Parikh,E.Chu,B.Peleato and J.Eckstein,Distributed optimization and statistical learning via the alternating direction method of multipliers,FoundationsandTrendsin MachineLearning,3:1(2011),1-122.

[27]R.Pytlak and T.Tarnawski,Preconditioned conjugate gradient algorithms for nonconvex problems with box constraints,NumerischeMathematik,116:1(2010),149-175.

[28]B.S.He and X.M.Yuan,On non-ergodic convergence rate of douglas-rachford alternating direction method of multipliers,NumerischeMathematik,130:3(2015),567-577.

[29]B.S.He and X.M.Yuan,On theo(1/n)convergence rate of the douglascrachford alternating direction method,SIAMJournalonNumericalAnalysis,50:2(2012),700-709.

[30]X.J.Cai,G.Y.Gu,B.S.He and X.M.Yuan,A proximal point algorithms revisit on the alternating direction method,SIAMJournalofmultipliersScienceChinaMathematics,56:10(2013),2179-2186.

[31]M.Tao,X.M.Yuan and B.S.He,Solving a class of matrix minimization problems by linear variational inequality approaches,LinearAlgebraandItsApplications,434:11(2011),2343-2352.

(editedbyLiangweiHuang)

∗This work was supported by the National Natural Science Foundation of China(11571074, 61170308),the Natural Science Foundation of Fujian Province(2015J01010),and the Major Science Foundation of Fujian Provincial Department of Education(JA14037).

†Manuscript received April 26,2015;Revised July 17,2015

‡Corresponding authors.E-mail:pzheng@fzu.edu.cn