DECOMPOSITION OF (1+1)-DIMENTIONAL,(2+1)-DIMENTIONAL SOLITON EQUATIONS AND THEIR QUASI-PERIODIC SOLUTIONS∗†

Qian Li

(Dept.ofMath.,ShanghaiUniversity,Shanghai200444,E-mail:liq689@163.com)

Xuemei Li

(Dept.ofMath.,ZhengzhouUniversity,Zhengzhou450052)

DECOMPOSITION OF (1+1)-DIMENTIONAL,(2+1)-DIMENTIONAL SOLITON EQUATIONS AND THEIR QUASI-PERIODIC SOLUTIONS∗†

Qian Li

(Dept.ofMath.,ShanghaiUniversity,Shanghai200444,E-mail:liq689@163.com)

Xuemei Li

(Dept.ofMath.,ZhengzhouUniversity,Zhengzhou450052)

A new spectral problem is proposed,and nonlinear diff erential equations of the corresponding hierarchy are obtained.With the help of the nonlinearization approach of eigenvalue problems,a new fi nite-dimensional Hamiltonian system onR2nis obtained.A generating function approach is introduced to prove the involution of conserved integrals and its functional independence,and the Hamiltonian fl ows are straightened by introducing the Abel-Jacobi coordinates.At last,based on the principles of algebra curve,the quasi-periodic solutions for the corresponding equations are obtained by solving the ordinary diff erential equations and inversing the Abel-Jacobi coordinates.

quasi-periodic solutions;Abel-Jacobi coordinates;Riemann-theta function

2000MathematicsSubjectClassification37K10;58F07;35Q35

1 Introduction

The confocal involutive system was fi rst systematically used by J.Moser[1]in the investigation of soliton equations such as the Korteweg-de Vries(KdV)equation.Nonlinearization method of eigenvalue problems[25]and constraint fl ow[6,7]are useful tools in the investigation of(1+1)-dimensional soliton equations,by which a class of new fi nite-dimensional integrable systems can be obtained.In the past few years,the nonlinearization method has been even successfully extended to obtain quasi-periodic solutions of(2+1)-dimensional soliton equations[3,4,8-10].Another interesting fact is that the confocal Lax matrix plays an important role in fi nding the involutive systems of finite-dimensional integrable systems,because the determinant of the Lax matrix is the generating function of the involutive systems. The Lax matrix has at least two important applications.First,it provides an important and eff ective way in finding new finite-dimensional integrable systems.Second,Abel-Jacobi coordinates,can be constructed concretely.

In the present paper,our main aim is to search for a new hierarchy of nonlinear evolution equations and to construct their algebro-geometric solutions.The outline of this paper is asfollows.In Section 1,we shallderive a hierarchy of(1+1)-dimensionaland(2+1)-dimensional soliton equations associated with the spectral problem(2.1)through Lenard’s gradient sequence.In Section 2,we shallintroduce the constraint between the potentials and eigenfunctins,a series of new fi nite-dimensionalHamiltonian system are obtained under the constraint, at the same time,a generating function approach is introduced to prove the integrability of these systems.In Section 3,by introducing the elliptic coordinates and the quasi-Abel-Jacobi coordinates,we prove the functionalindependence of conserved integrals,from which we prove that the Hamiltonian system is completely integrable.In Section 4,by introducing a set of polynomial integrals,we arrive at the decomposition of the soliton hierarchy.In Section 5,we are going to construct the Abel-Jacobi coordinates,by whichHk-flow can be straightened.In Sections 6 and 7,quasi-periodic solutions of soliton equations are obtained with the help of Jacobi-inversion.

2 Lenard Spectral Problem and Soliton Equations

Consider the following spectral problem:

whereφ=(q,p)T,andr1is an arbitrary constant.

Consider thet-part of the spectral problem(2.1)

We introduce the Lenard gradient sequence{gj}by the Lenard recursive equation

where

with△=(lnv+r1)/v.The equationJg-1=0 has a special solutiong-1=(0,0,1)T.

ThenV=σλ(gλ)satisfies

thus detσλ(gλ)is a constant along thexfl ow.We adopt

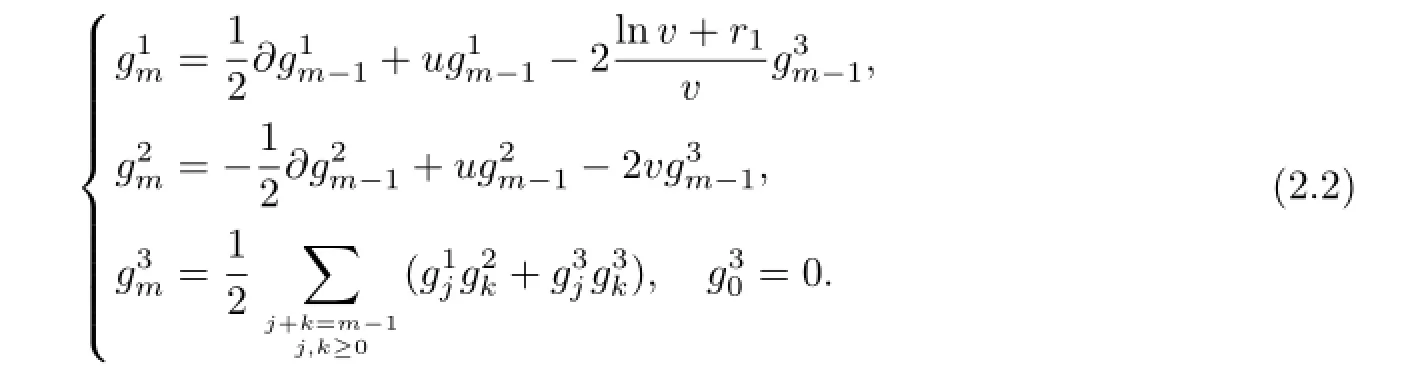
The fi rst few numbers of the Lenard gradient{gj}are

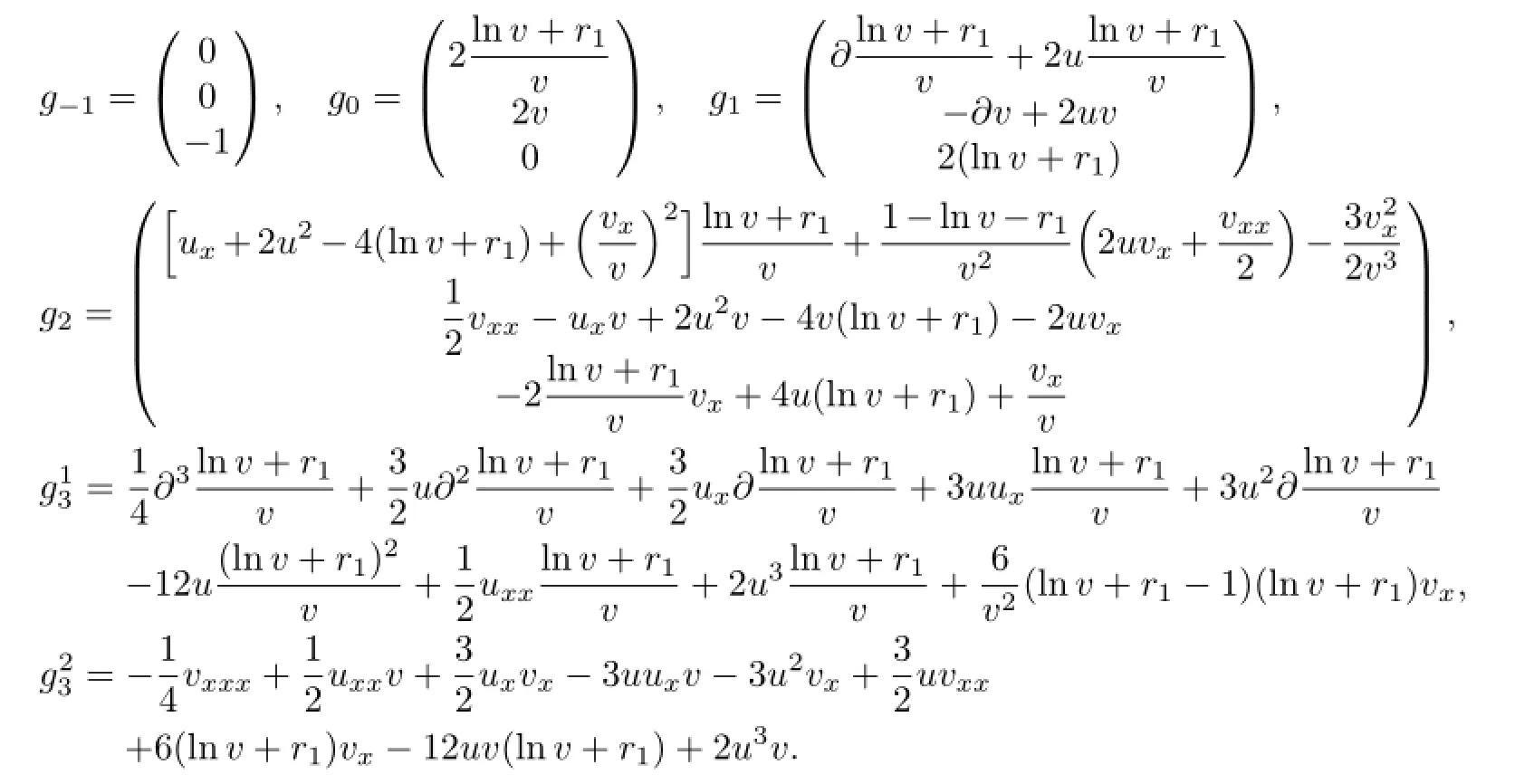
Let us consider the polynomial ofλ

where

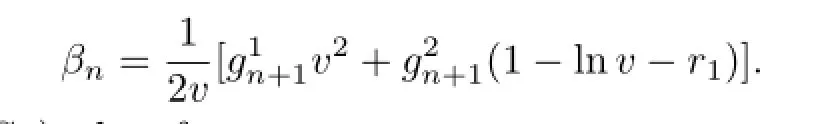
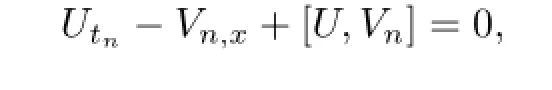
we get

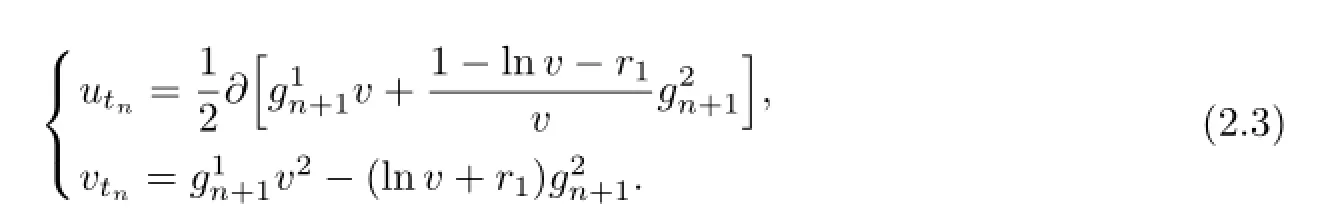
Therefore,we can define the vector fi elds

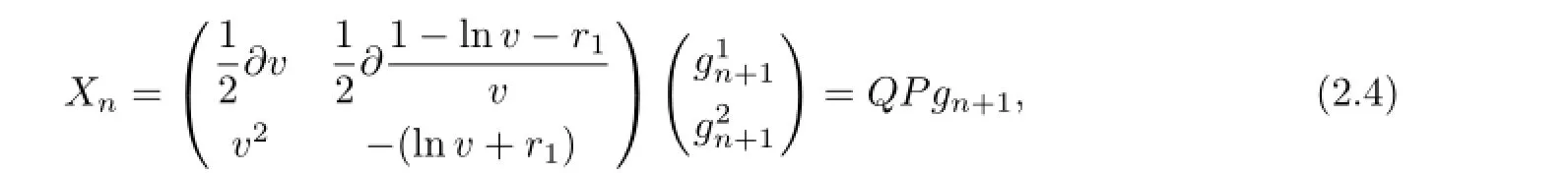
wherePis the projective map:

Denotingt1=yandt2=t,we have

Letvbe a compatible solution of(2.5)and(2.6),and defi ne

After direct calculations we have

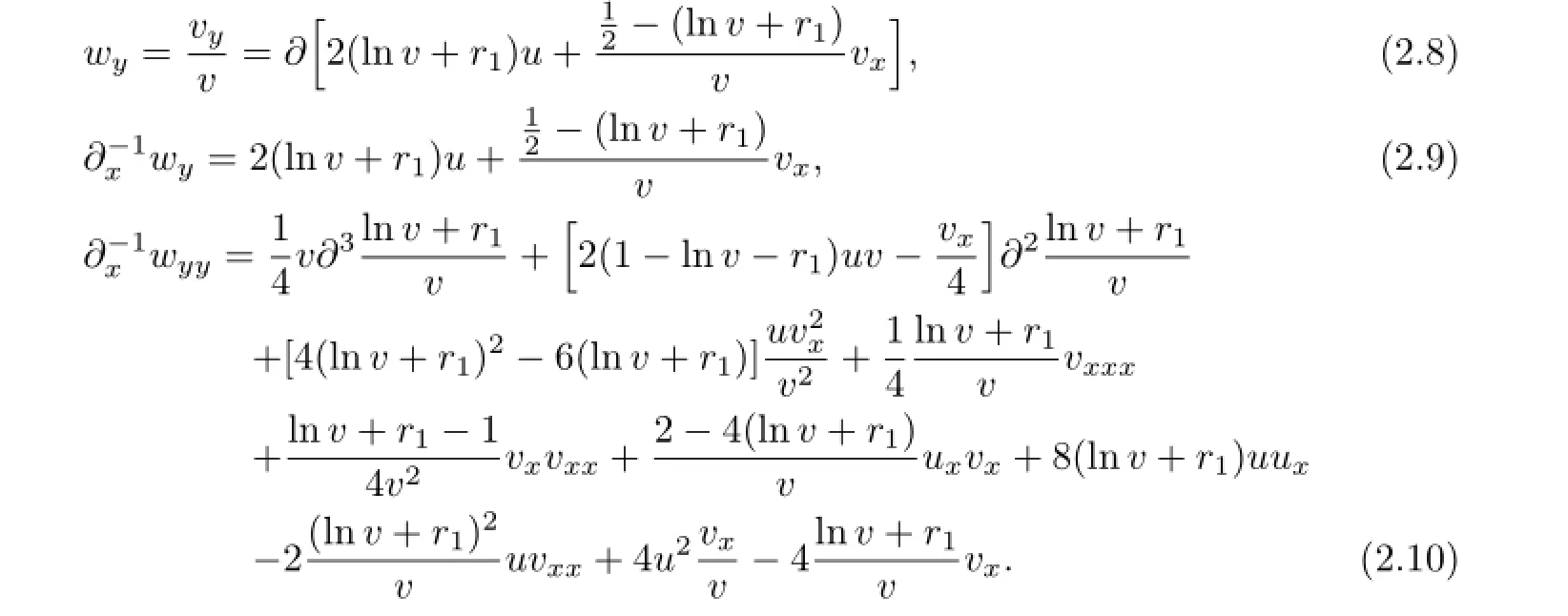
From(2.7)and(2.8)we have

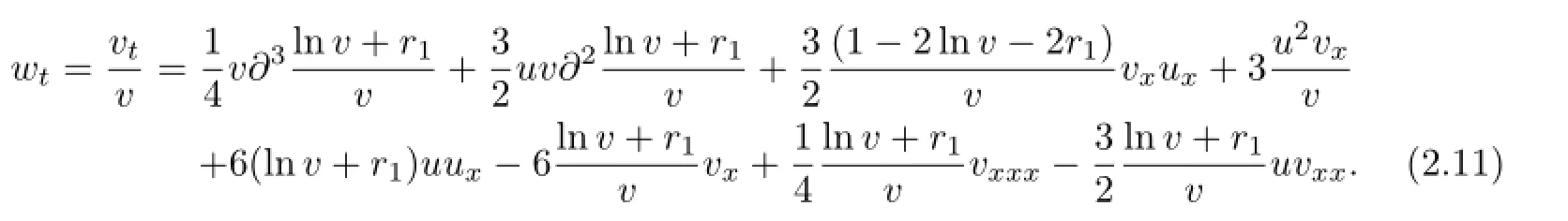
Substituting(2.7),(2.10)into(2.11)we can get the following(2+1)-dimensional KP equation

3 The Nonlinearization of Eigenvalue Problem and the Involutivity of Conserved Integrales

ConsiderNcopies of the linear equation(2.1)

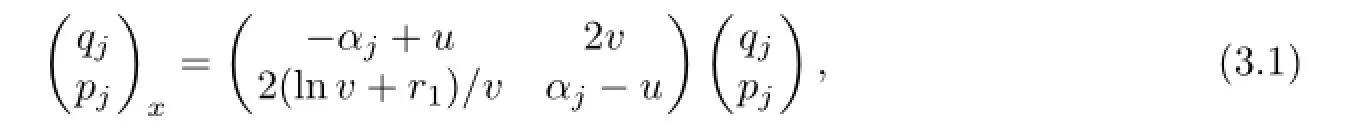
with distinct eigenvaluesα1,···,αN.LetA=diag(α1,···,αN),and define a mapτλ

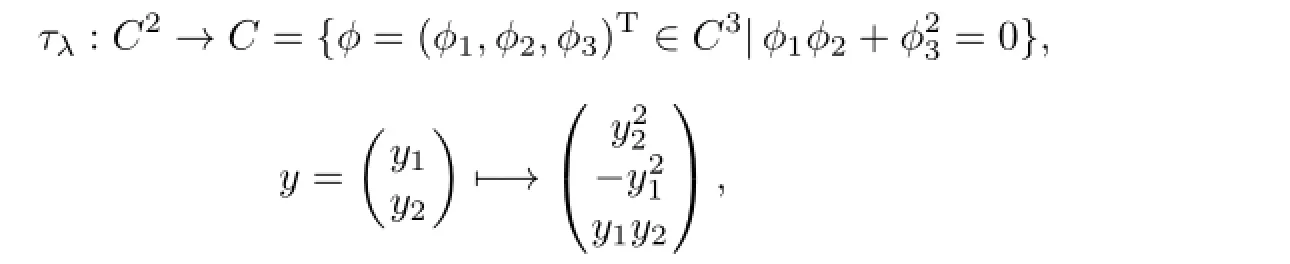
then

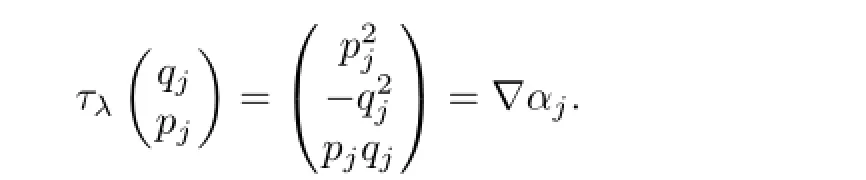
From(3.1)we have the following fundamental identity

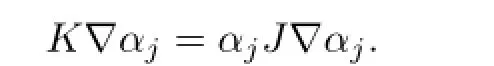
The solution of the Lenard eigenvalue problem with general parameterλis constructed as

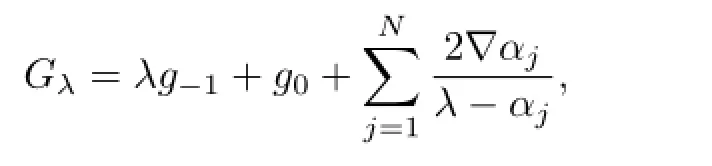
Proposition3.1If

then

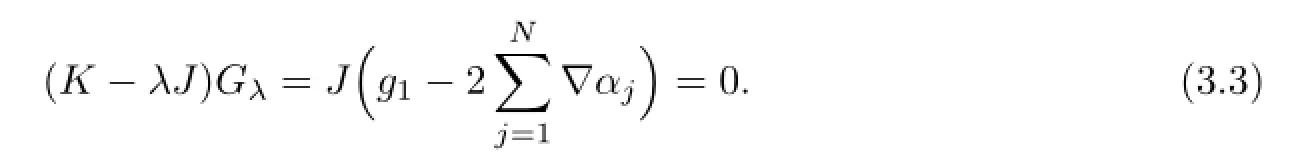
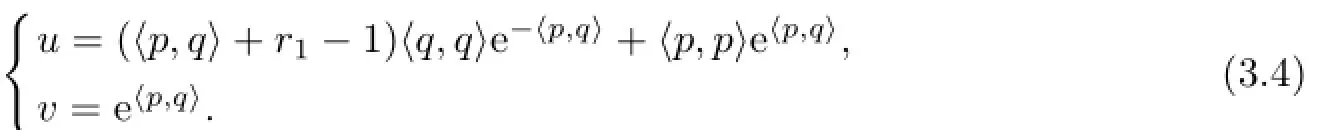
Since the potentialsu,vin(3.1)satisfy Bargmann constrait,substituting(3.4)into(3.1), then the spectral problem can be nonlinearized

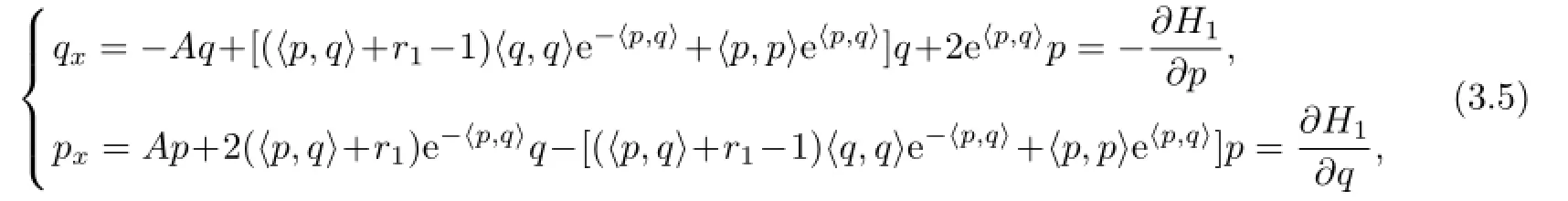
where

From(K-λJ)Gλ=0,the stationary Lax equationVx-[U,V]=0 has a solution alongx-flow

then from the definition ofGλwe have

where

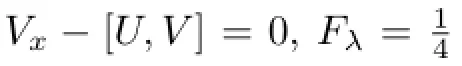
where

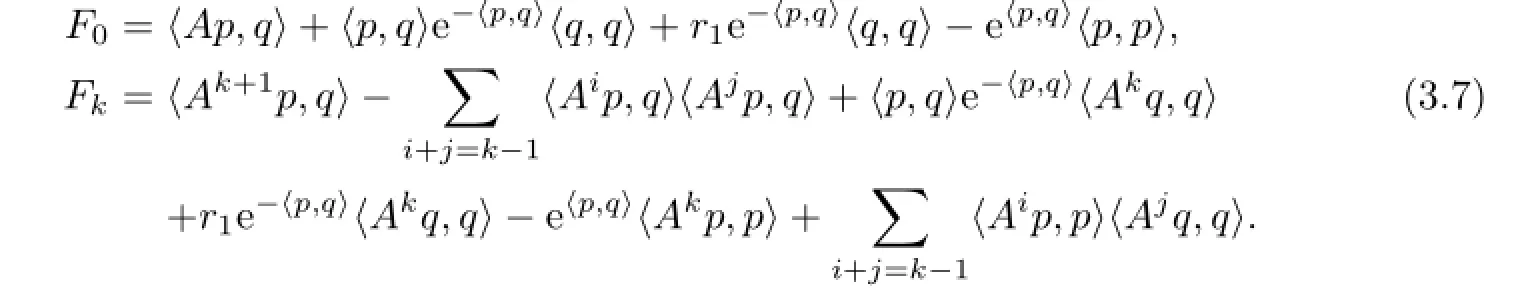
Regarding the generating functionFλas a Hamiltonian in the symplectic space(R2N,dqΛdp), the canonical equation is

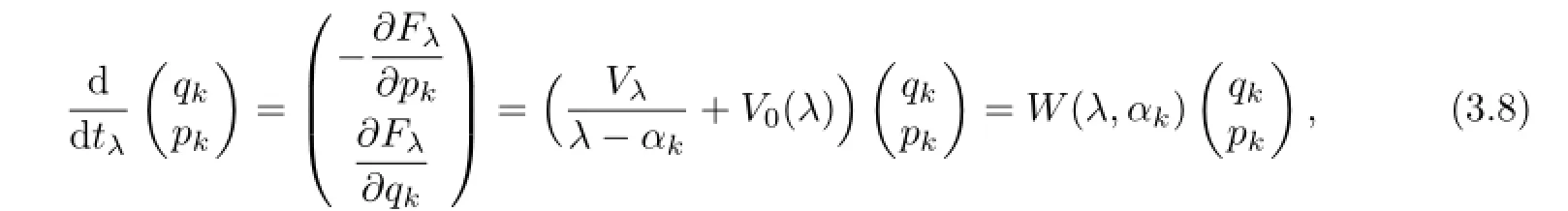
where

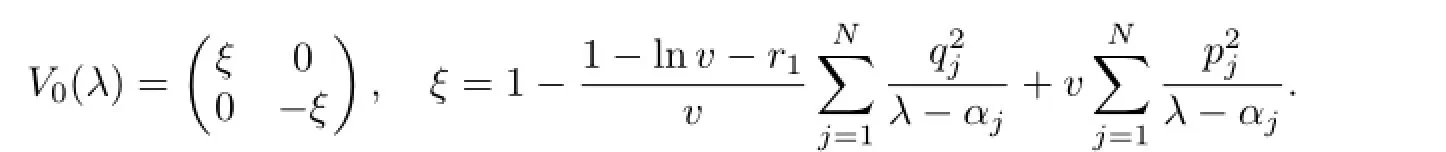
Proposition3.2TheLaxmatrixVµsatisfiestheLaxequationalongtheFλflow

Corollary3.1

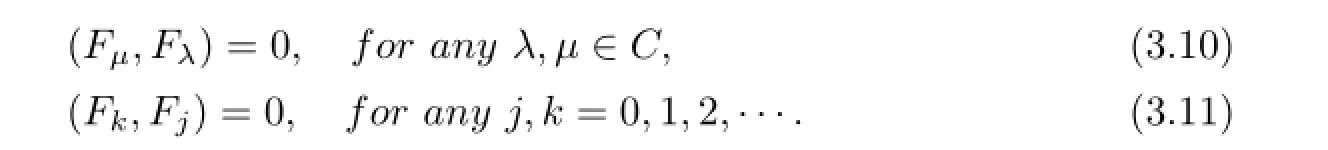
ProofEquation(3.9)implies thatFµ=detVµis invariant along thetλ-flow.And the derivative of the functionFµalong theFλ-fl ow is exactly the Poisson bracket,then we have

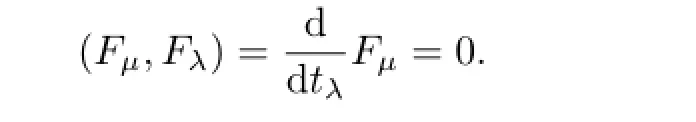
Because

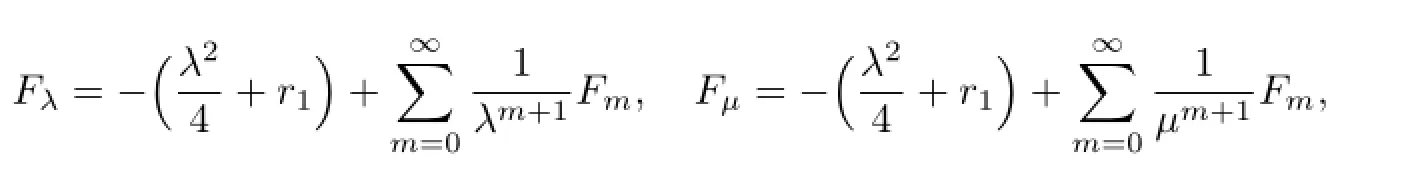
4 Elliptic Coordinates and Function Independence

It is easy to see that each one ofFλ,V12λandV21λ,as a rational function ofλ,has simple poles atαj.We have

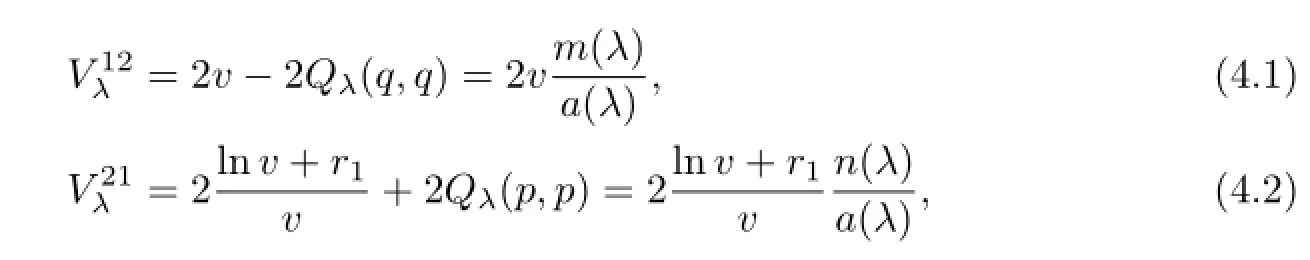
where

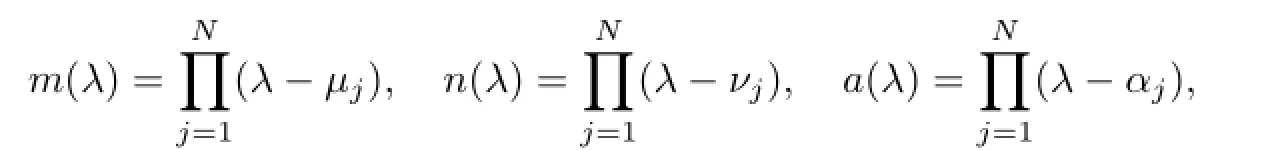
and the roots{µk},{νk}are defined as elliptic variables[12].If we expandfollowing the power ofλ-1,and by comparing the coeffi cients of the same power ofλwe have

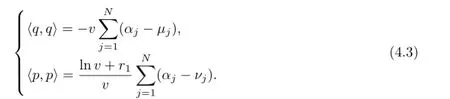
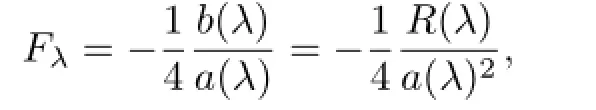
where

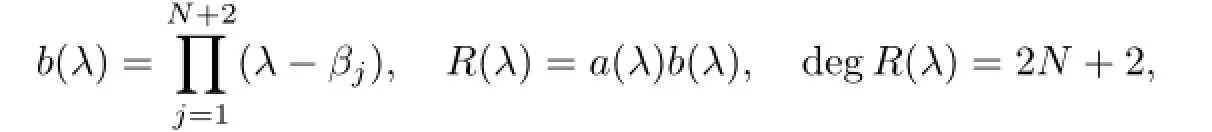
then

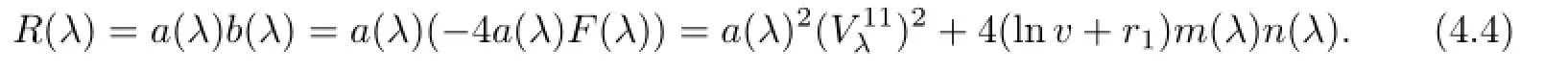
Proposition4.1Theellipticcoordinatessatisfytheevolutionequationsalongthetλflow

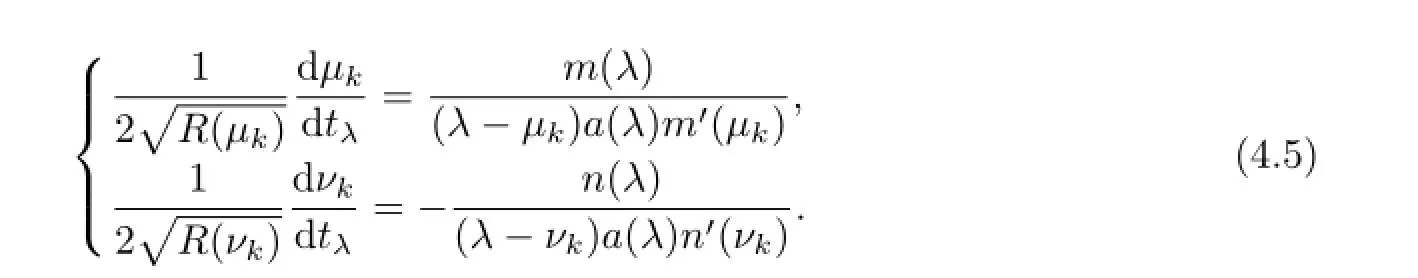
ProofSubstitutingλ=µk,νk,into(4.1),(4.2),respectively,we have

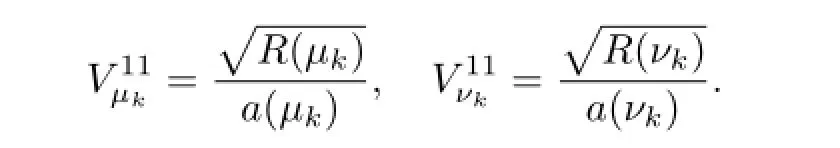
The evolution equation ofVµ,µ∈Γalong thetλ-flow is

the second and third components of equation(4.6)are

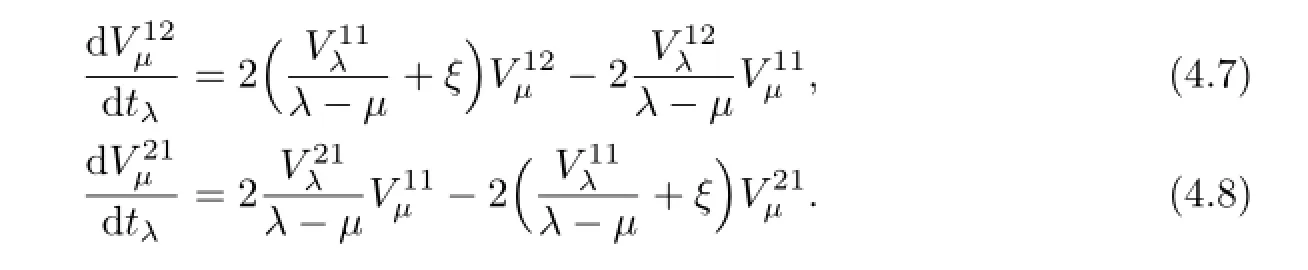
Letµ=µk,µ=νk,respectively.After some calculations we have(4.5).

Since

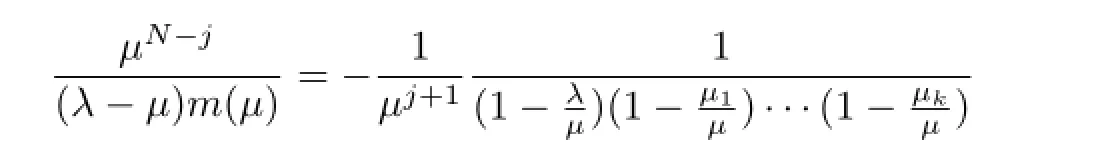
whenj≥1,the coeffi cients ofµ-1in the Laurant expansion is 0,then from Cauchy integral theorem we have

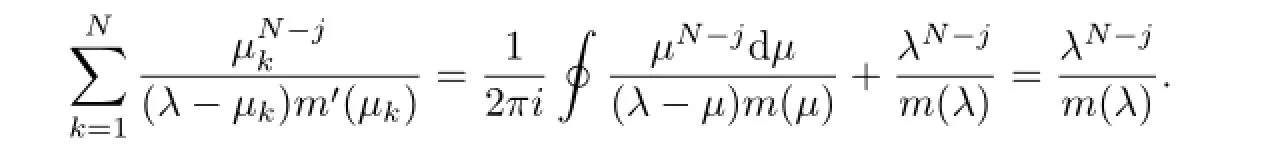
For the fixedλ0,introduce the quasi-Abel-Jacobi coordinates

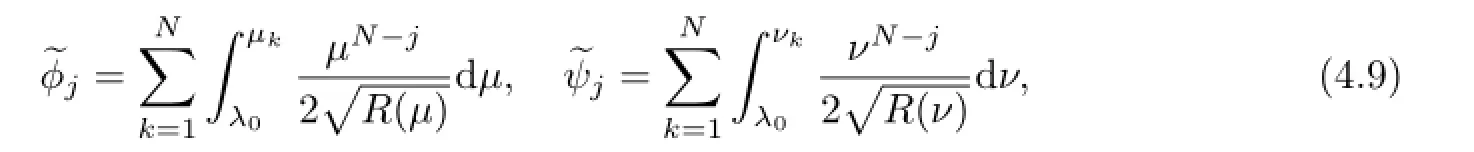
and we have the following proposition.

Proposition4.2(Straightening of theFλflow)

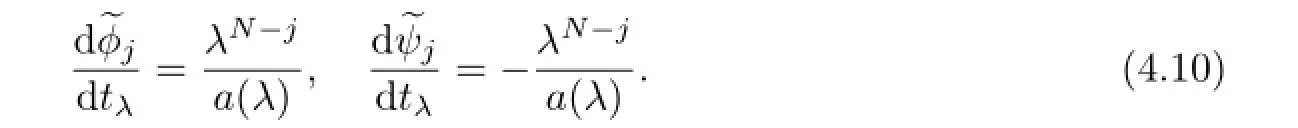
Corollary4.1(Straightening of theFkflow)LettkbethevariableoftheFkflow,then wehave

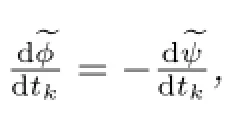
whereAjarethecoefficientintheexpansion

with

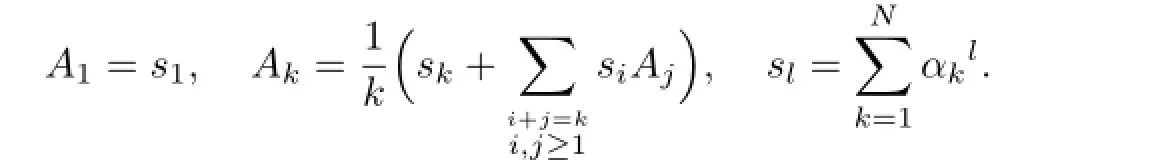
ProofAccording to the defi nition of the Possion bracket:

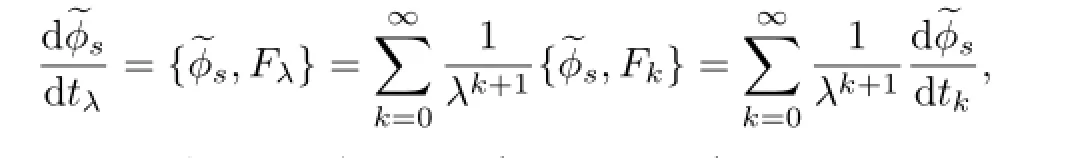
with the supplementary defi nitionA-k=0(k=1,2,···).By comparing the coeffi cients ofλ-k-1in(4.10),we derive

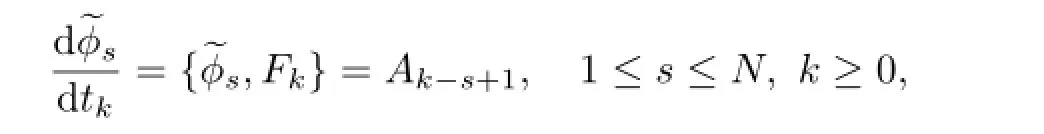
hence

Proposition4.3F0,F1,···,FN-1givenin(3.7)arefunctionalindependent.

ProofWe only need to prove the linear independence of the diff erentials dF0,dF1,···,dFN-1.Recall the expression of the Possion bracket by means of the symmetric structure

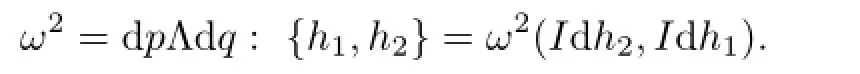
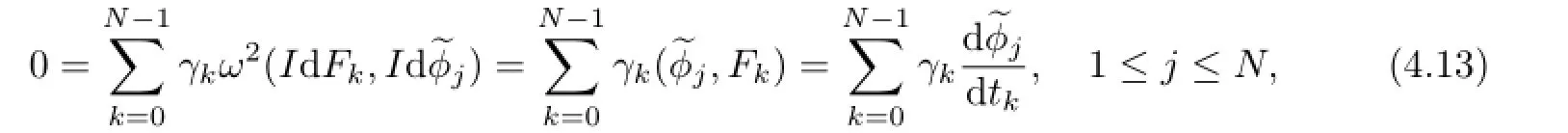
Henceγ0=···=γN-1=0,since the coeffi cient determinant is equal to 1 by equation (4.11).

5 The Decomposition of Solition Equations

The kernel ofJis of dimension 1 with the generatorg-1.ExertingJ-1Kon(3.2)ktimes,since each time there is an extra termcjg-1,hence we have

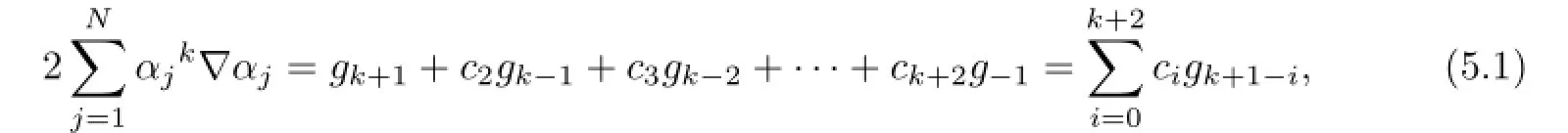
wherec0=1,c1=0,c2=2r1,ckis a constant.

Proposition5.1Letq(x),p(x)beasolutionoftheBargmannsystem(3.5).Then

solvestheNthstationaryequation

ProofDefi ne a polynomial

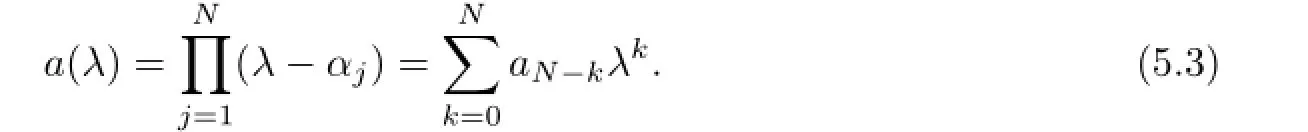
Multiplying byaN-kand summing withkfrom 0 toN,equation(5.1)becomes

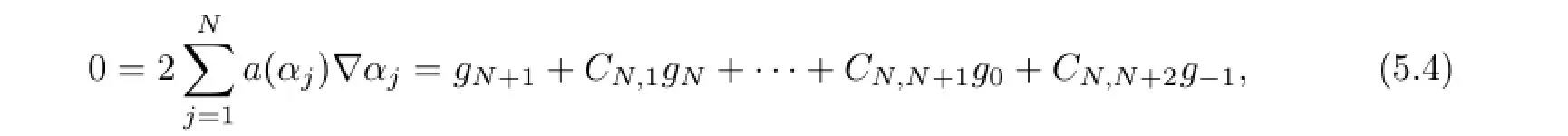
where

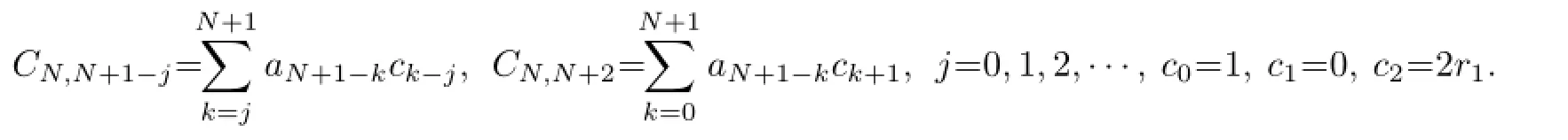
Acting withQPon equation(5.4)yields(5.2).

Proposition5.2Undertheconstraint(5.1),thefunctionsGλandgλhavethefollowing directrelation

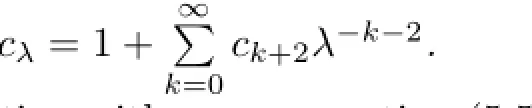
Acting withσλon equation(5.5)thus we have

Based oncλ=1-2Hλ,we introduce another generating functionHλ,then we have

According to

it is not diffi cult to obtain

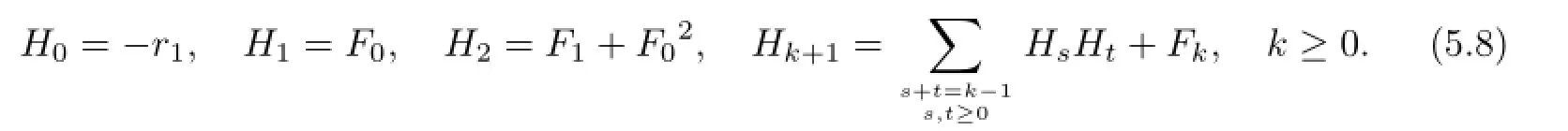
Proposition5.3{Hk}satisfiestheLiouvilleconditionsofcompletelyintegrability

1.{Hµ,Hλ}=0,foranyλ,µ∈C,{Hj,Hk}=0,foranyj,k=0,1,2···.

2.H1,H2,···,HNarefunctionalindependent.

Denote the solution variety of equations(3.5)and(5.2)byNandMrespectively.By Proposition 5.1,fmapsNintoM.Consider the canonical equation of theHk-fl ow

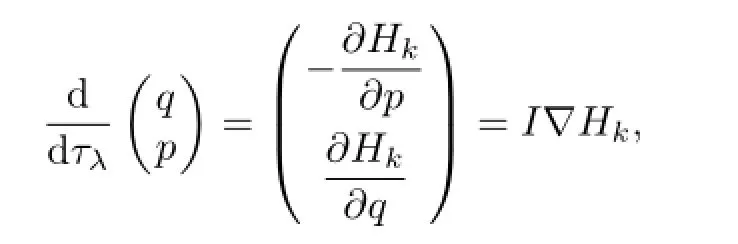
and the solution of the initial value problem

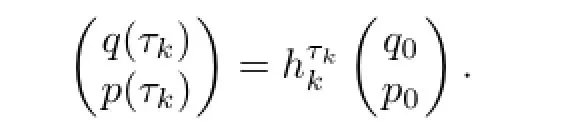
It is well-known that the involutionimplies the commutativity ofandHenceI∇Hkcan be regarded as a vector fi eld onN.The importance ofHkis that the diff erentialf∗mapsI∇Hkexactly intoXk-1restricted toM. From(3.4)and(3.8),after some calculations we have

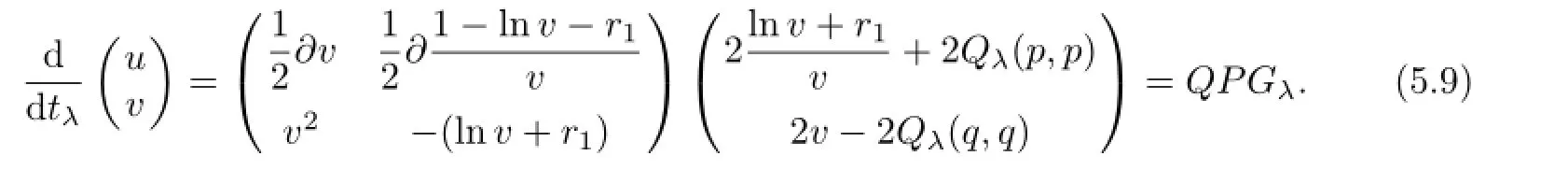
Proposition5.4

ProofFrom the canonical equation(3.8)of thetλfl ow we get

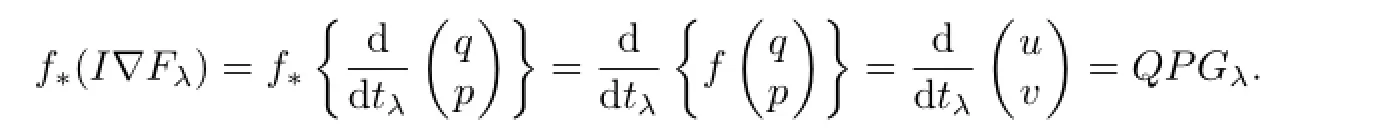
From(5.8)we have

Hence we have the fi rst part.The second part is obtained by comparing the coeffi cients of the same powerλ-k-1.

Corollary5.1Inthecasek=2,denoteτ1=x,τ2=y.Let(q(x,y),p(x,y))Tbea compatiblesolutionof

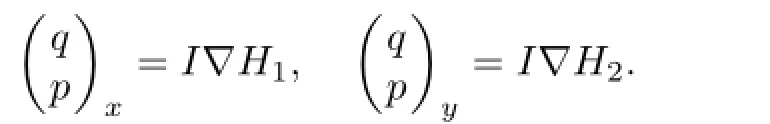
Thenu(x,y)andv(x,y),whichareobtainedfromBargmannconstraint(3.4)solvessoliton equation(2.5).

Corollary5.2Inthecasek=3,denoteτ1=x,τ3=t.Let(q(x,t),p(x,t))Tbea compatiblesolutionof

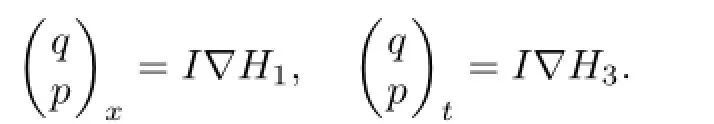
Thenu(x,t)andv(x,t)whichareobtainedfromBargmannconstraint(3.4)solvessoliton equation(2.6).

Proposition5.5Let(q(x,y,t),p(x,y,t))TbeacompatiblesolutionofH1,H2,H3,thensolves(2+1)-dimensionalsolitonequation(2.12).

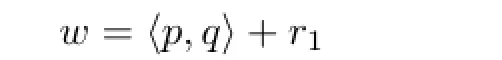
6 Evolution Picture Via the Abel-Jacobi Coordinates

The shape of equation(4.9)suggests the consideration of the holomorphic diff erential

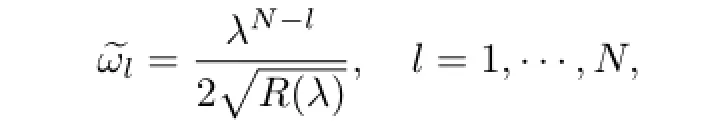
on the hyperelliptic curveΓ:ζ2-4R(λ)=0,with the genusN.Take the canonical basis of cycles onΓ:a1,b1,···,aN,bN,which satisfi es

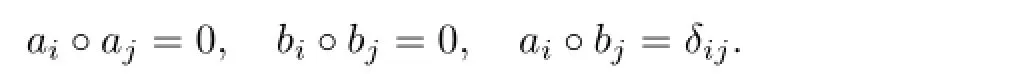
LetC=(Cjl)NNbe the inverse of the periodic matrix(Ali)NN:

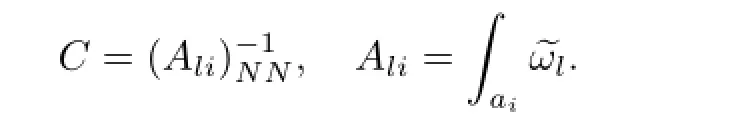
Then for the normalized holomorphic diff erential

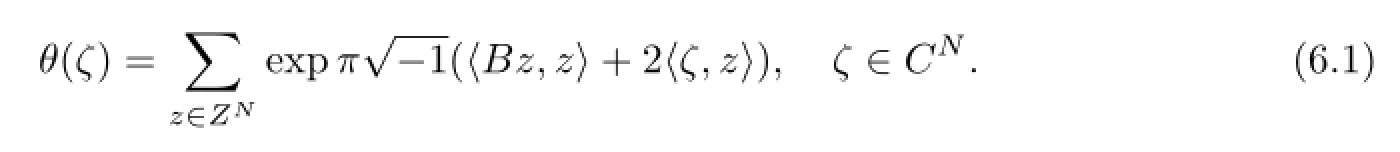
For the fixedλ0,we defi ne Abel-Jacobi coordinates

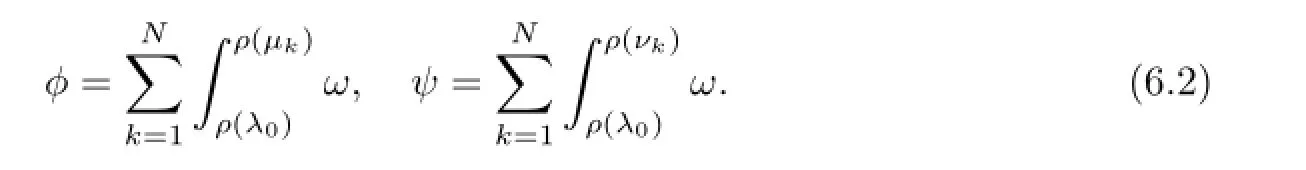
Since degR(λ)=2N+2,for the sameλ,there are two points on diff erent sheets of the Riemann surfaceΓ

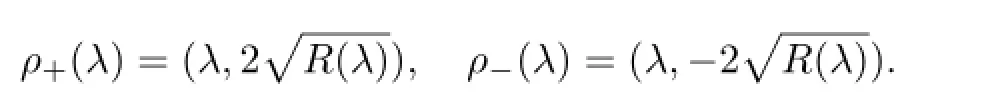
At∞,the affi ne equationζ2=4R(z-1)is transformed into

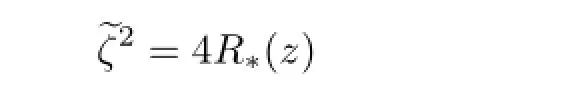
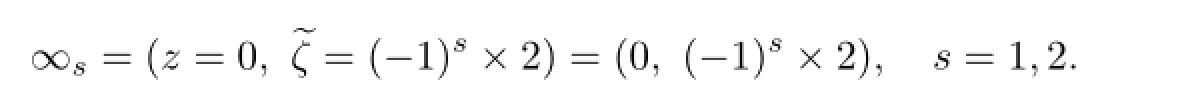
LetC1,···,CNbe the column vector ofC,then by direct calculations we have the following conclusions.

Corollary6.1

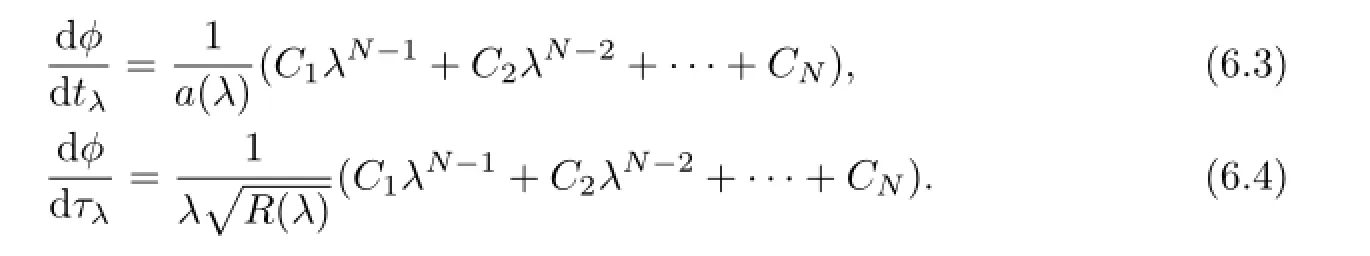
Corollary6.2Let,thenthecoefficientsof

satisfytherecursiveformula

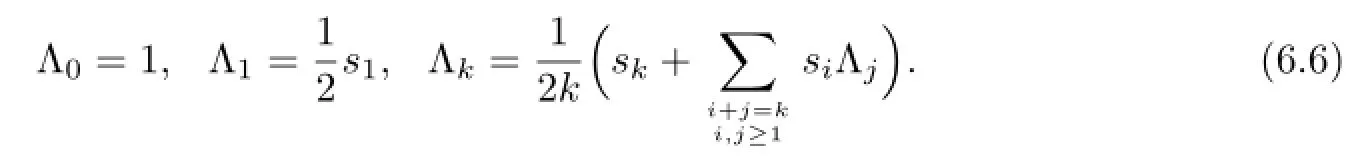
Corollary6.3Thecoefficientsof

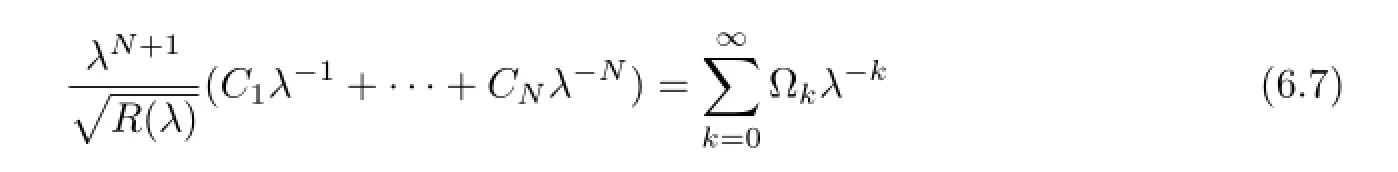
are

withΛ-s=0,s=1,2,···.Specifically

Therefore we have the following proposition.

Proposition6.1Theτk-flowisstraightenedbytheAbel-Jacobicoordinates

The straightened equations(6.9)are easily integrated by quadraturesThrough the definition of the Abel-Jacobi coordinatesφ(as well asψ),

(1)

(2)

7 Inversion fromφ,ψto{µk},{νk}

The Abel mapA:Div(Γ)is defi ned by

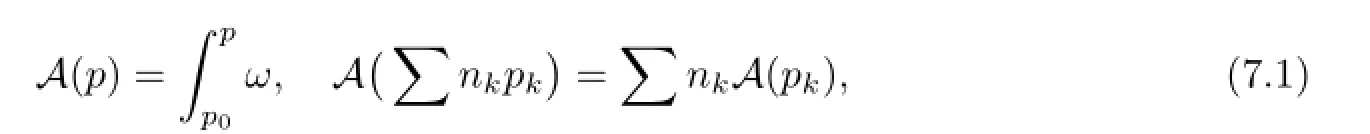
wherep0=ρ(λ0)is fi xed,Div(Γ)is the divisior group,and the LatticeTis spanned by the periodic vectors{δj;Bj},which are the column vectors ofEand(Bjs).The defi nition of Abel-Jacobi coordinates is rewritten as

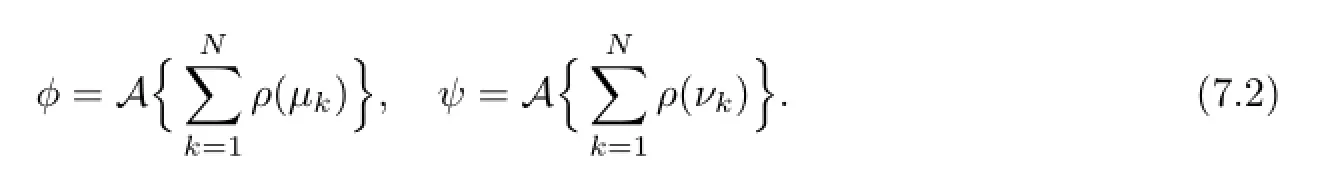
According to the Riemann Theorem,there exists a constant vectorKsuch that

(i)θ(A(ρ(λ))-φ-K)has exactlyNzeros atλ=µ1,···,µN,

(ii)θ(A(ρ(λ))-ψ-K)has exactlyNzeros atλ=ν1,···,νN.

And we have the inversion formula

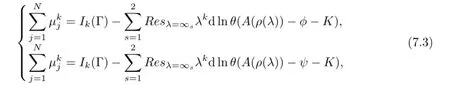
where

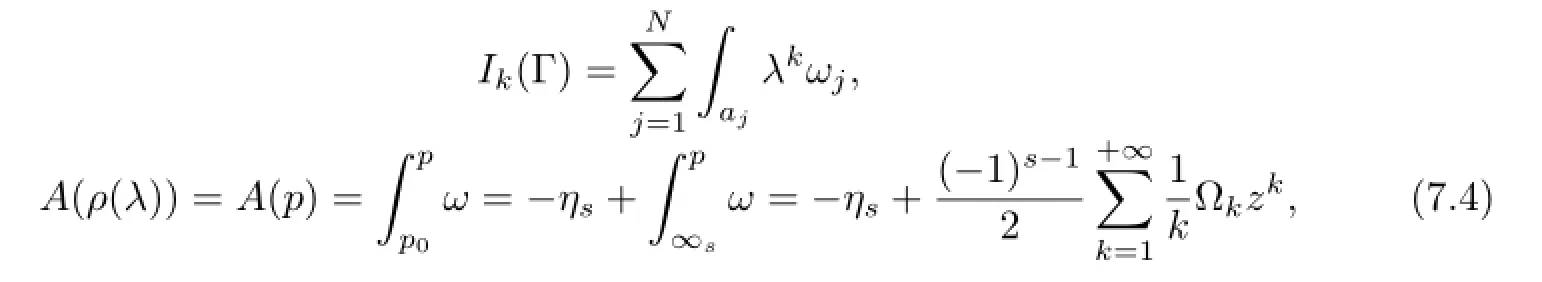
with

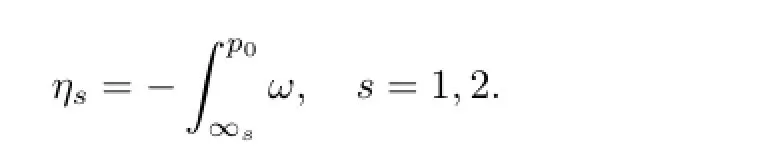
Hence we have the power series expansion near∞sin the local coordinatesz=λ-1

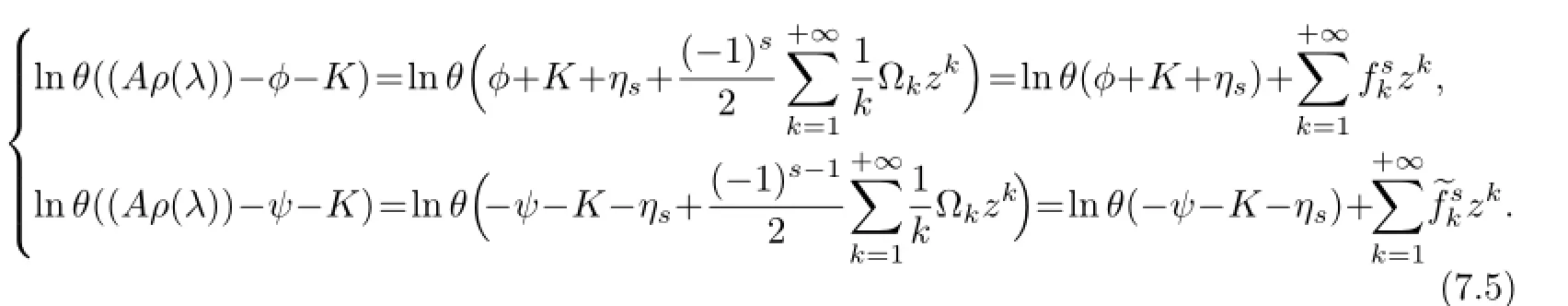
Here the factθ(ζ)=θ(-ζ)is used.The power sums are obtained after substituting(7.5) into(7.3)

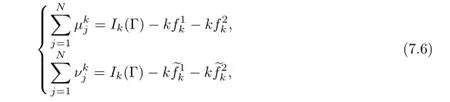
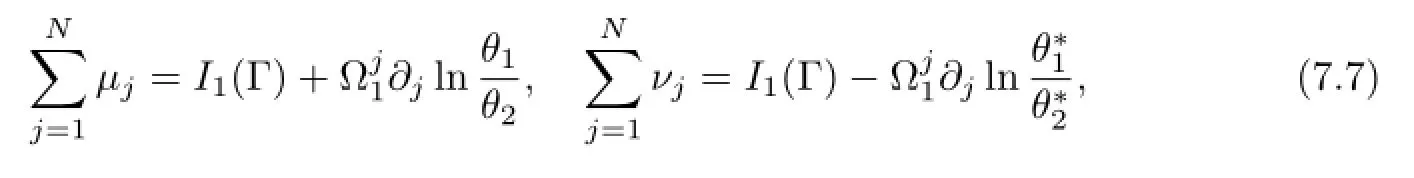
where

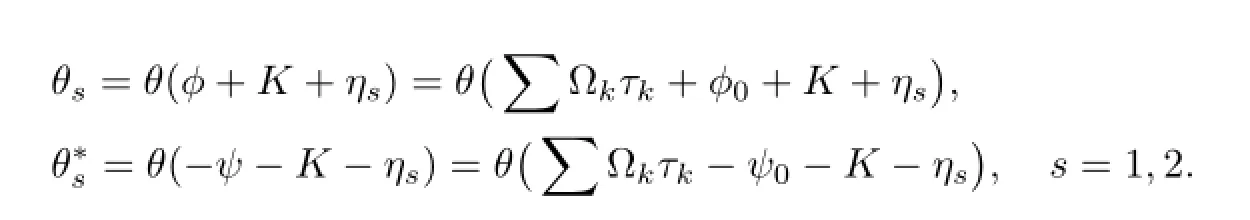
Denotex=τ1,y=τ2,t=τ3.Then equation(7.7)is further simplifi ed as

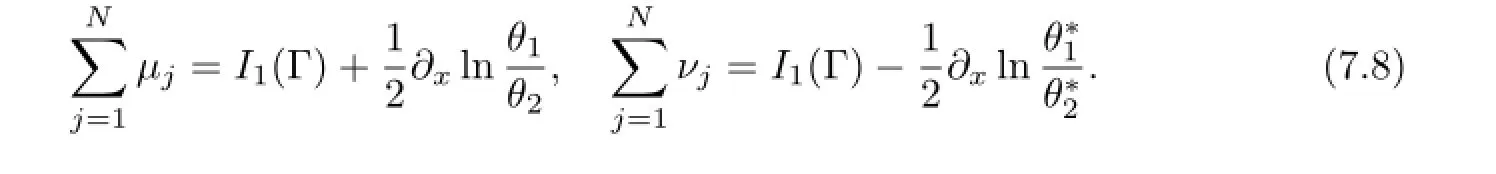
8 Quasi-periodic Solutions

From(3.4),(3.5)and(4.3),the potentialsuandvcan be expressed by elliptic coordinates

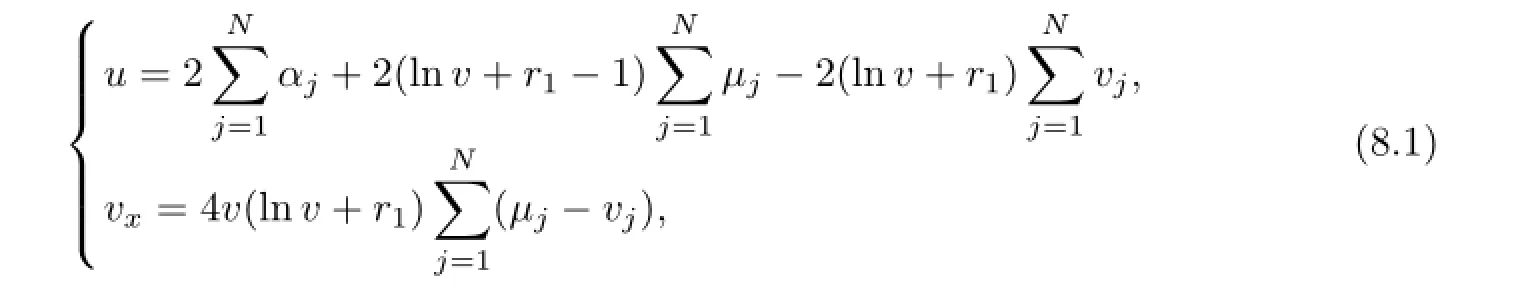
Substituting(7.8)into the second equation of(8.1),we obtain

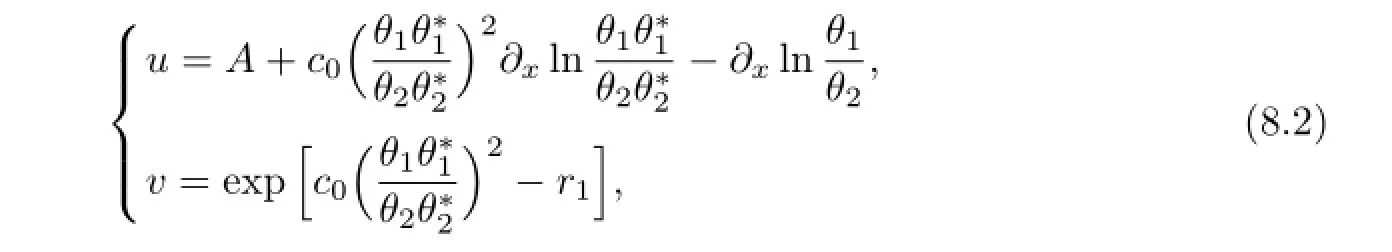
where

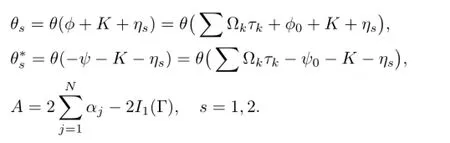
Proposition8.1(1+1)-dimensionalsolitonequation(2.5)hasasolution

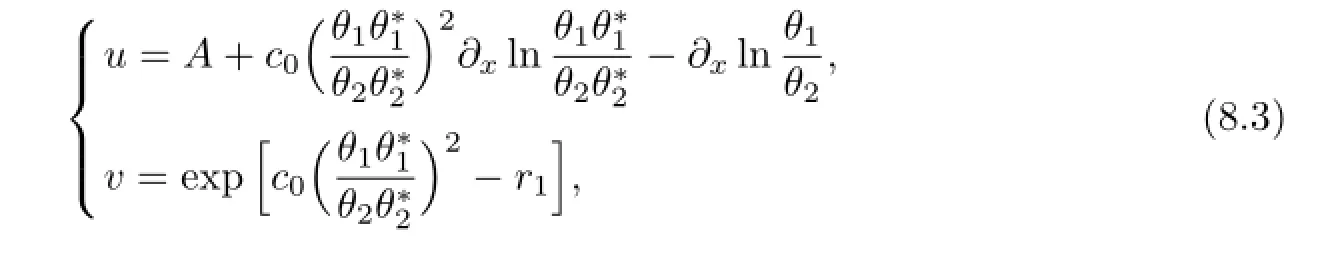
where

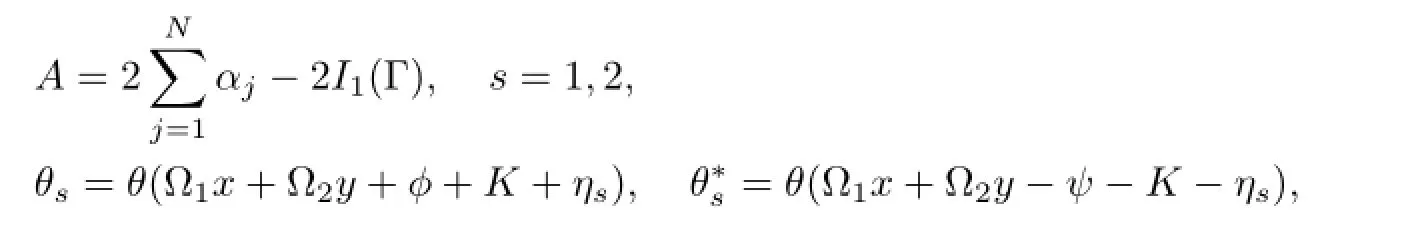
c0areindependentofτ1=x,τ2=y,butdependentuponτ3=t,τ4=···.

Proposition8.2(1+1)-dimensionalsolitonequation(2.6)hasasolution

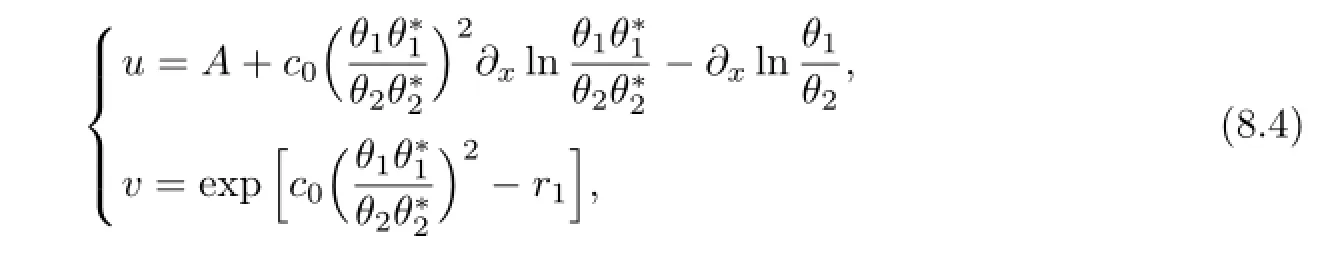
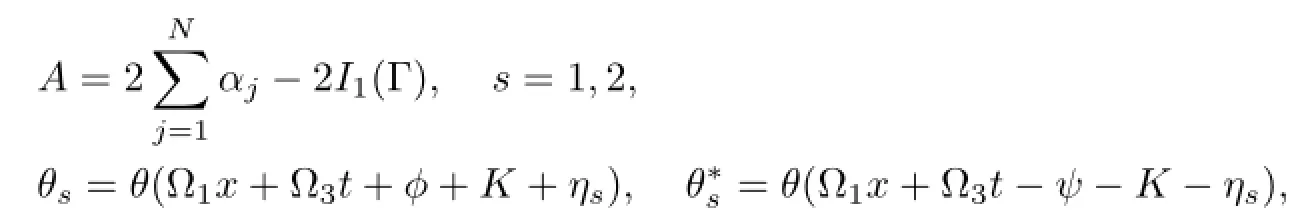
wherec0areindependentofτ1=x,τ3=t,butdependentuponτ2=y,τ4=···.

Proposition8.3(2+1)-dimensionalsolitonequation(2.12)hasasolution

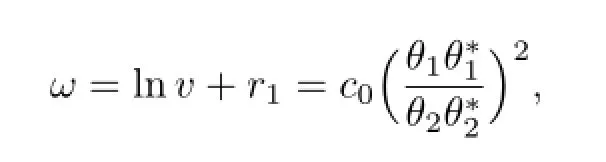
where

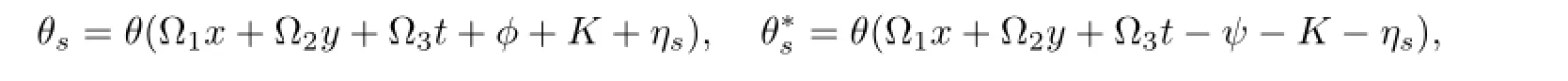
c0areindependentofτ1=x,τ2=y,τ3=t,butdependentuponτ4=···.

[1]J.Moser,Integrable Hamiltonian system and spectraltheory,in Proceedings ofthe 1983 Beijing Symposium on Diff erential Geometry and Diff erential Equations,Beijing:Science Press,1986.

[2]C.W.Cao,X.G.Geng,Nonlinear Physics,Research Reports in Physics,edited by C.Gu et al.,Springer,Berlin,1990.

[3]C.W.Cao,Nonlinearization of the Lax system for AKNS hierarchy,Sci.China,33A(1990),528-536.

[4]C.W.Cao,X.G.Geng,On quasi-periodic solutions of the 2+1 dimensional Caudrey-Dodd-Gibbon-Kotera-Sawada equation,Phys.Lett.A,256(1999),59-65.

[5]C.W.Cao,Y.T.Wu,X.G.Geng,Relation between the Kadometsev-Petviashvili equation and the confocal involutive system,J.Math.Phys.,40(1999),3948-3970.

[6]M.Antonowicz,S.Rauch-Wojciechowski,Restricted flows of soliton hierarchies:coupled KdV and Harry Dym case,J.Phys.A:Math.Gen.,14(1991),5043-5061.

[7]M.Antonowicz,S.Rauch-Wojciechowski,How to construct finite-dimensional bi-Hamiltonian systems from soliton equations:Jacobi integrable potentials,J.Math.Phys.,33(1992),2115-2125.

[8]J.S.Zhang,Y.T.Wu,X.M.Li,Quasi-periodic solution of the(2+1)-dimensional Boussinesq-Burgers soliton equation,Phys.A,319(2003),213-232.

[9]X.G.Geng,Y.T.Wu,C.W.Cao,Quasi-periodic solutions of the modifi ed Kadomtsev-Petviashvili equation,J.Phys.A:Math.Gen.,32(1999),3733-3742.

[10]X.G.Geng,C.W.Cao,H.H.Dai,Quasi-periodic solutions for some(2+1)-dimensionalintegrable models generated by the Jaulent-Miodekhierarchy,J.Phys.A:Math.Gen.,34(2001),989-1004.

[11]X.G.Geng,C.W.Cao,Quasi-periodic solutions of the 2+1 dimensional modifi ed Korteweg-de Vries equation,Phys.Lett.A,261(1999),289-296.

[12]P.Gri.ths,J.Harris,Principles of Algebraic Geometry,Wiley,New York,1994.

[13]D.Mumford,Tata Lectures on Theta I,II,Birkhauser,Basel,London,1984.

(editedbyLiangweiHuang)

∗This work was supported by Natural Science Research Project of Henan Education Department under Grant No.2011B110024.

†Manuscript received November 29,2014