ON THE SETS OF GˆATEAUX NON-DIFFERENTIABILITY OF LIPSCHITZ ISOMORPHISM BETWEEN BANACH SPACES∗†

Yingbin Ruan

(Dept.ofMath.,FujianNormalUniversity,Fuzhou350007,E-mail:rybfjnu@163.com)

ON THE SETS OF GˆATEAUX NON-DIFFERENTIABILITY OF LIPSCHITZ ISOMORPHISM BETWEEN BANACH SPACES∗†

Yingbin Ruan

(Dept.ofMath.,FujianNormalUniversity,Fuzhou350007,E-mail:rybfjnu@163.com)

We prove that for every Lipschitz isomorphismffrom a separable Hilbert spaceHto a Banach spaceYwith Radon-Nikod´ym property,there is a bounded surjective linear operatorT:H→Yso that(f+T)-1(NG(f-1))is aΓ-null set ofH,whereNG(f-1)is the set of all the points of Gˆateaux non-diff erentiability off-1.

Lipschitz isomorphism;Gˆateaux diff erentiability;Γ-null sets

2000MathematicsSubjectClassification26B05;28B05

1 Introduction

In infinite dimensional Banach spaces there is no naturalanalogue of Lebesgue nullsets. Various measure theoretic notions ofnullsets were introduced there in order to generalize the theorem of Rademacher to infi nite dimensional Banach spaces:Iffis a Lipschitz mapping from a separable Banach space to a Banach space with the Radon-Nikod´ym property(RNP), then it is Gˆateaux diff erentiable“almost everywhere”,where a Banach spaceYis said to have the Radon-Nikod´ym property(RNP)if every Lipschitz functionf:R→Yis diff erentiable almost everywhere.In this case,there are several nonequivalent ways to defi ne appropriate notions of negligible sets,for example,Haar null sets[1],Gauss null sets[2],Aronszajn null sets[3]andΓ-null sets[4](see[5]for the survey of the topic except theΓ-null sets).The concept of a set beingΓ-null was introduced by Lindenstrauss and Preiss in[4],and the connection betweenΓ-null sets and diff erentiability of Lipschitz functions were investigated in[4,6].We state now the main existence theorem for Gˆateaux derivatives.This is a infi nite-dimensional version of Rademacher’s theorem.

Theorem1.1[4]ALipschitzmappingfofaseparableBanachspacetoaBanachspace withtheRadon-Nikod´ympropertyisGˆateauxdifferentiable“almosteverywhere”,thatis,the setNG(f)ofGˆateauxnon-differentiabilitypointsoffisΓ-null.

In their paper[4],Lindenstrauss and Preiss asked whetherf(NG(f))isΓ-null whenfis a Lipschitz equivalence from a separable Banach spaceXwith the RNP onto a Banach spaceY,that is,fis surjective andfor anyx,y∈X,for some constantM.If the answer to this problem were positive it would solve the problem whether Lipschitz equivalence implies isomorphism(for separable spaces with the RNP).Indeed,this would imply with the help of Theorem 1.1 that there is anx0∈Xsuch thatfis Gˆateaux diff erentiable atx0andf-1is Gˆateaux diff erentiable atf(x0),thenDf(x0)is a surjective isomorphism.

In this paper,we discuss this problem and prove that,for Lipschitz isomorphismffrom a separable Hilbert spaceHto a spaceYwith RNP,there is a bounded surjective linear operatorT:H→Yso that(f+T)-1(NG(f-1))isΓ-null set ofH,whereNG(f-1)is the set of all the points of non-Gˆateaux diff erentiability off-1.

2 Preliminaries

Letfbe a function defi ned on an open set in a Banach spaceXinto a Banach spaceY. The functionfis said to have a derivative atx0in the directionuif

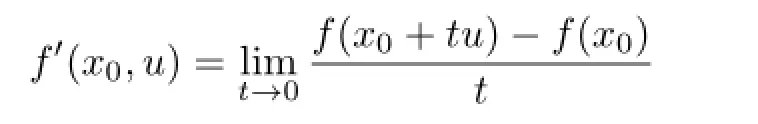
exists.

The functionfis said to be Gˆateaux diff erentiable atx0if there is a bound linear operatorT:X→Ysuch that for everyu∈X,

The operatorTis called the Gˆateaux derivative offatx0and is denoted byDf(x0).Denote G(f)to be the set of all points of Gˆateaux diff erentiability off.

Next we list some obvious diff erentiation rules and a simple lemma for our purpose.Iffis continuous and linear,thenfis its own Gˆateaux derivative.If the compositionf◦gis defi ned,gandfare Gˆateaux diff erentiable atx0and atg(x0)respectively and iffis Lipschitz,thenf◦gis Gˆateaux diff erentiable atx0and the usual chain rule formula holds

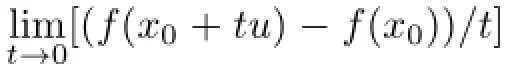
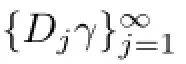
A Borel setNof a Banach spaceXis calledΓ-null set iffor residually manyγ∈Γ(X).Recall that a set is called residual if its complement is of the first category.A possibly non-Borel setA⊂Xis calledΓ-null if it is contained in a Borel Γ-null set.

TheΓ-null sets are clearly defined in aσ-ideal of subsets ofX.For more information on theΓ-null sets,see Lindenstrauss and Preiss[4].

Lemma2.2[4]IfXisseparable,thenthesetisresidualin

Lemma2.3[4]LetXbeseparableandYhavetheRNP.TheneveryLipschitzfunctionf:X→YisGˆateauxdifferentiableoutsideaΓ-nullset.Inparticular,µ(γ-1(N))=0

3 Main Results

As the properties of the diff erentiability of the real value functions on Rn,we also have the following basic properties.

Lemma3.1LetDbeanopensetofRnandXbeaBanachspace.Letξ=(t1,···,tn)∈D.ThenthemappingγfromDintoXsatisfiesthefollowingproperties:

(i)IfγisGˆateauxdifferentiableatξ,thenthepartialderivativesDkγ(ξ),k=1,2,···,n existand

(ii)IfthemapγhascontinuouspartialderivativesDkγ(ξ)(k=1,2,···,n)onsome neighborhoodofξ,thenγisGˆateauxdifferentiableatξ.

Lemma3.2Letγ:beacontinuousfunctionandfbeaLipschitzfunction fromXintoY.Givenα=(t1,t2,···)∈Ω,ifthemappings

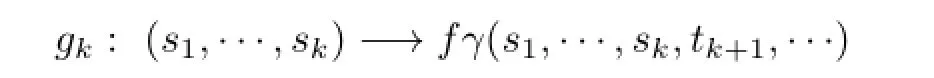
and

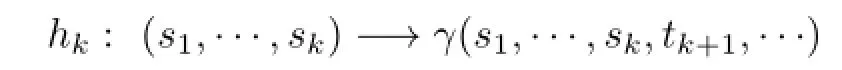
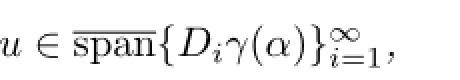
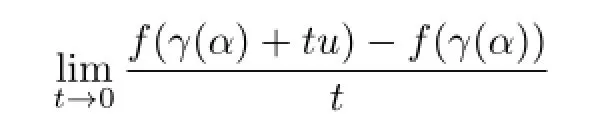
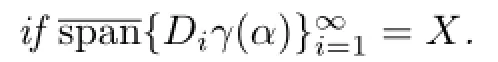
ProofLetk∈N.Since the mappinghkis diff erentiable atαk=(t1,···,tk),by Lemma

3.1 and a simple calculation,we have

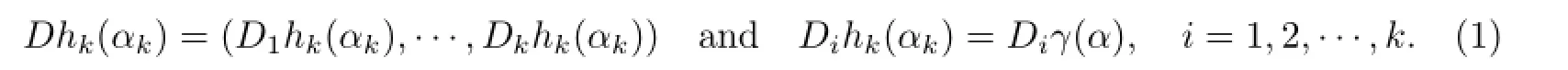
Then,by(1),u=Dhk(αk)βk.It is clear thatandgk(αk+Then,we have the following equality:

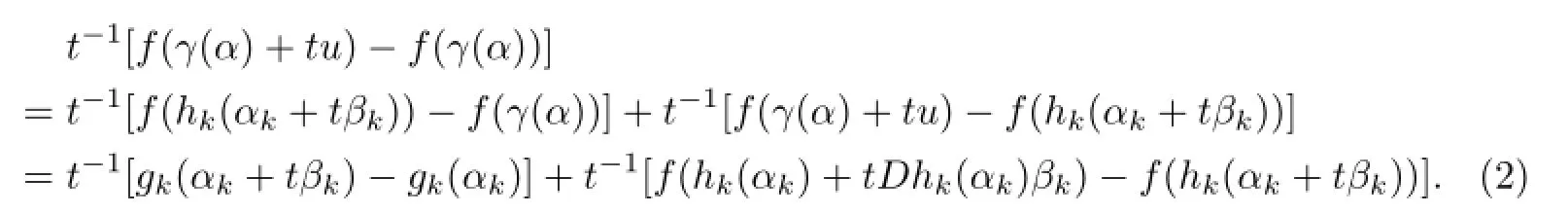
Sincefis Lipschitz,hkandgkare diff erentiable atαk,it follows that

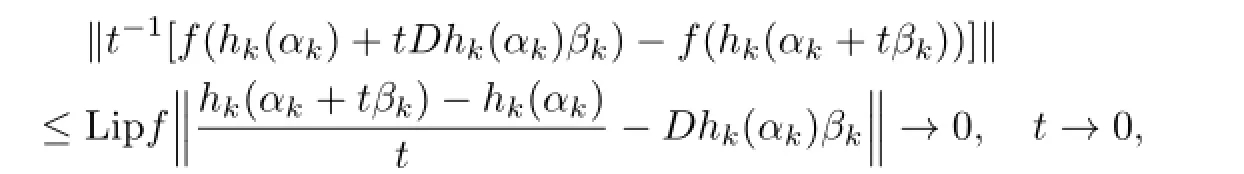
and the limit

exists.It follows from the equality(2)that the directional derivative

Theorem3.1LetXbeaseparableBanachspace,andYbeaspacewithRNP.Let fbeaLipschitzisomorphismfromXontoY,andassumethatthereexistsaGˆateaux differentiablepointy0∈Yoff-1sothatDf-1(y0)YiscomplementedinX.Thenthere existsaboundedlinearsurjectiveoperatorTfromXintoYsuchthat(f+T)-1(N)isaΓ-nullsetofX,whereNisthesetofallthepointsofnon-Gˆateauxdifferentiabilityoff-1.

ProofNote that the derivativeoff-1aty0is an injective linear operator with closed range fromXtoYby the equivalence of the Lipschitz mapf-1.Hence the operatorhas an inverse operator fromontoYwhich is denoted also by

Takec＞Lipand putIt is clear thatTX=Y. We also claim that,for everyx∈G(f),the operatoris invertible onY,hereIYis the identicaloperator onY,and hence we havefor anyx∈G(f).In fact,since

for anyx∈G(f),we have

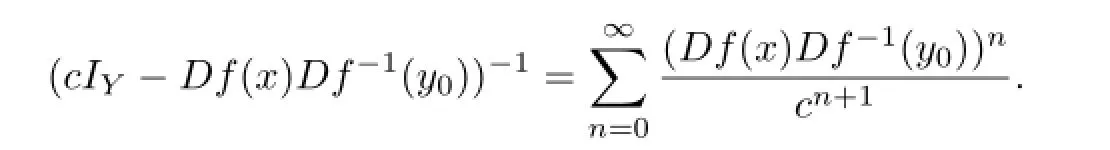
Hence,for eachx∈G(f),

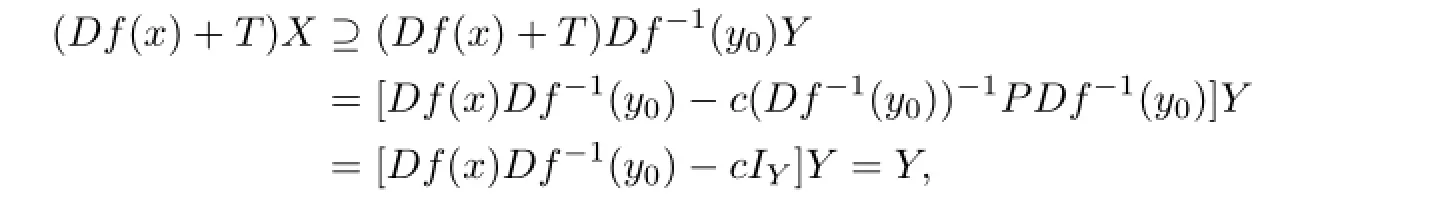
so

Letthenfor anyα∈Ω,that is,

Sincef+Tis Lipschitz,it follows that,for eachα∈γ-1(G(f)),

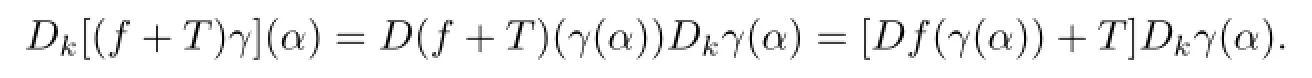
Then,by(3),for everyα∈γ-1(G(f)),we have the following equality:

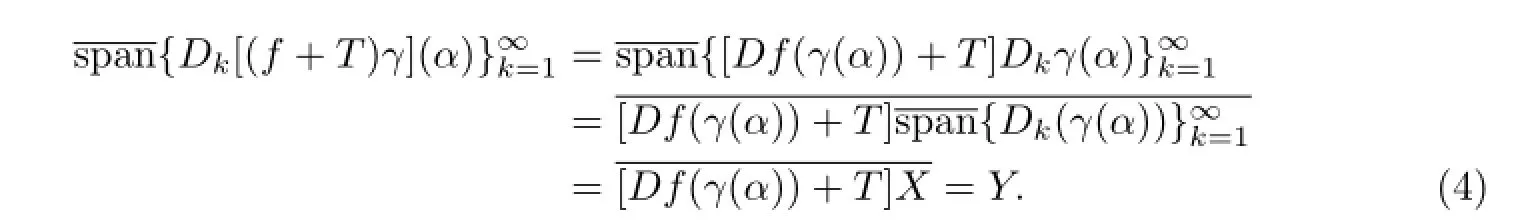
Sinceγhas continuous partial derivatives,andf-1are all Lipschitz functions,it follows from Lemma 3.1 that,for everythe mappings

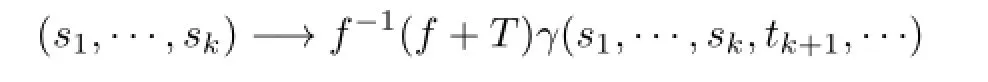
and

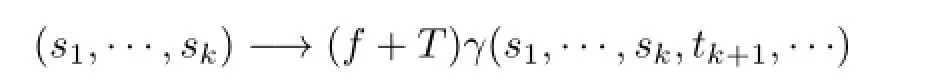
are diff erentiable atαk=(t1,···,tk),k=1,2,···.By the equality(4),it follows from Lemmas 2.3 and 3.2 thatf-1is Gˆateaux diff erentiable at(f+T)(γ(α))for almost everyα∈Ω.It implies that the product Lebesgue measure

This proves the theorem.

Theorem3.2LetHbeaseparableHilbertspace,andfbeaLipschitzisomorphism fromHontoaspacewithRNP.ThenthereexistsaboundedlinearsurjectiveTfromHto Ysuchthat(f+T)-1(N)isaΓ-nullset,whereNisthesetofallthepointsofnon-Gˆateaux differentiabilityoff-1.

ProofSince Lemma 2.3 implies thatf-1has points of Gˆateaux diff erentiability,this completes the proof by the fact that every closed subspace of Hilbert space is complemented and Theorem 3.1.

Corollary3.1LetHbeaseparableHilbertspace,andfbeaLipschitzisomorphism fromHontoaspaceYwithRNP.ThenthereexistaboundedlinearsurjectiveTfromHtoY andasubsetM⊂HwhosecomplementinHisaΓ-nullsetsuchthatandM⊂G(f).

ProofFrom Theorem 3.1,Lemma 2.3 and the fact that the union of twoΓ-null sets is aΓ-null set,the corollary obviously holds.

[1]J.P.R.Christensen,On sets of Haar measure zero in abelian Polish groups,IsraelJ.Math.,13(1972),255-260.

[2]R.R.Phelps,Gaussian null sets and diff erentiability of Lipschitz maps on Banach spaces,PacificJ.Math.,77(1978),253-531.

[3]N.Aronszajn,Diff erentiability of Lipschitzian mappings between Banach spaces,StudiaMath.,57(1976),147-190.

[4]J.Lindenstrauss,D.Preiss,On Fr´echet diff erentiability of Lipschitz maps between Banach spaces,AnnalsofMath.,157(2003),257-288.

[5]Y.Benyamini,J.Lindenstrauss,Geometric nonlinear functional analysis vol.I,Colloquium Pub.vol.48,Amer.Math.Soc.no.48,Providence,Rhode Island,2000.

[6]J.Lindenstrauss and D.Preiss,On Fr´echet diff erentiability of Lipschitz functions and porous sets in Banach spaces,Annals of Mathematics Studies,No.179,Princeton University Press, New Jersey 2012.

(editedbyLiangweiHuang)

∗Research was supported by the National Natural Science Foundation of China(11171066)and the Natural Science Foundation of Fujian Province(2013J01003).

†Manuscript received March 10,2015