STABILITY OF SOLUTIONS FOR CERTAIN THIRD-ORDER NONLINEAR STOCHASTIC DELAY DIFFERENTIAL EQUATIONS∗

A.M.A.Abou-El-Ela,A.I.Sadek,A.M.Mahmoud,E.S.Farghaly

(1.Dept.ofMath.,FacultyofScience,AssiutUniversity,Assiut71516,Egypt; 2.Dept.ofMath.,FacultyofScience,NewValleyBranch,AssiutUniversity,NewValley, El-Khargah72111,Egypt,E-mail:math ayman27@yahoo.com(A.M.Mahmoud))

STABILITY OF SOLUTIONS FOR CERTAIN THIRD-ORDER NONLINEAR STOCHASTIC DELAY DIFFERENTIAL EQUATIONS∗

A.M.A.Abou-El-Ela1,A.I.Sadek1,A.M.Mahmoud2,E.S.Farghaly1

(1.Dept.ofMath.,FacultyofScience,AssiutUniversity,Assiut71516,Egypt; 2.Dept.ofMath.,FacultyofScience,NewValleyBranch,AssiutUniversity,NewValley, El-Khargah72111,Egypt,E-mail:math ayman27@yahoo.com(A.M.Mahmoud))

In this paper,we investigate stochastic asymptotic stability of the zero solution for certain third-order nonlinear stochastic delay diff erential equations by constructing Lyapunov functionals.

asymptotic stability;Lyapunov functional;stochastic delay diff erential equations;third-order nonlinear diff erential equations

2000MathematicsSubjectClassification34K20;34K50;60H35

1 Introduction

Recently,there has been a growing interest in the eff ects of noise on dynamical systems with delays.In biological systems,both noise and delays are inevitable.Noise is immanent in any open system involving up-take and dissipation of energy.Delays usually arise due to finite information transmission times.In this context,delayed visual feedback systems, stochastic resonance and oscillator ensembles with delayed interactions,synchronization of human movements,fi eld theoretical models of brain activity,and disturbed speech control due to delayed auditory feedback(the so-called Lee eff ect)have been studied.Furthermore, as an alternative to motor controlmodels without delays,stochastic models with delays have been proposed to describe postural sway(see[4]and the references therein).

Delay diff erential equations have been extensively developed in the past several decades see[3,5,6,10,13].Stochastic delay diff erential equations were fi rst introduced by Itˆo and Nisio[7]in which the existence and uniqueness of the solutions have been investigated.

In the last several decades,numerous studies have been developed toward the study of stochastic delay diff erential equations,such as stochastic stability,Lyapunov functional method,Lyapunov exponent,stochastic flow,invariant measure,invariant manifold,numerical approximation and attraction etc.(see[8,9,12,14,16-20,27]and the references therein). However many basic issues remain unsolved even for a simple linear equation with constant coeffi cients.

Moreover the Lyapunov’s method has also been developed to investigate the stability of stochastic functional diff erential equations or stochastic delay diff erential equations since 1970s,see[7,16,20].In[11],Kolmanovskiiand Shaikhet presented an interesting survey of ageneral method of Lyapunov functionals construction for stochastic diff erential equations of neutral type.

It is worth-mentioning that there has been little work on the stability of stochastic delay diff erential equations(e.g.[1,2]),although there are several papers on the stability of delay diff erential equations.

The aim of this paper is to investigate the stochastic asymptotic stability of the zero solution for the third-order stochastic delay diff erential equations of the form

and

whereandσ2are positive constants;andγ2are two positive constants which will be determined below.sup(t)∈Rmis a standard Wiener process or Brownian motion;andf3(x) are continuous functions;g1(0)=f1(0)=f3(0)=0.

For the deterministic case,that is,whenσ1x(t)=0 in equation(1.1)andσ2x(t-h(t))= 0 in equation(1.2),such problems have been studied recently by severalauthors(e.g.[21,23-25,28]).This paper is to extend their results to the stochastic case,but the mathematical techniques employed here are very much diff erent from the previous ones.

2 Notations

We start by introducing notations that will be used throughout the paper.

R+denotes the set of all real non-negative numbers.

Rndenotes then-dimensional Euclidean space.

Rn×mdenotes the space of all(n×m)matrices with real entries.

Ωdenotes the sample space.

Fdenotes theσ-fi eld of subsets ofΩ(whence(Ω,F)is a measurable space).

Pdenotes the probability measure on(Ω,F)(that is,it is closed with respect to the set-theoretic operations executed a countable number of times).

(Ω,F,{F}t≥0,P)denotes the complete probability space with a filtration{F}t≥0satisfying the usual conditions(that is,it is fi ltered by a nondecreasing right-continuous family{F}t≥0of sub-σ-fi elds ofF.

3 Stability

Letbe anm-dimensional Wiener process defined on the probability space.Consider ann-dimensional stochastic diff erential equation

with initialvaluex(0)=x0∈Rn.We assume thatf:andsatisfy the local Lipschitzian condition and the linear growth condition for the existence and uniqueness of the solutions for equation(3.1)(See,for example,[15,22,26]).It is therefore known that equation(3.1)has a unique continuous solution ont≥0,which is denoted byx(t;x0)in this paper.Assume furthermore thatf(t,0)=0 andg(t,0)=0,for allt≥0. Hence the stochastic diff erential equation admits the zero solutionx(t;0)≡0.

Definition3.1The zero solution for the stochastic diff erential equation is said to be stochastically stable or stable in probability,if for every pair ofε∈(0,1)andr＞0,there exists aδ=δ(ε,r)＞0 such that

whenever|x0|＜δ.Otherwise,it is said to be stochastically unstable.

Definition3.2The zero solution for the stochastic diff erential equation is said to be stochastically asymptotically stable,if it is stochastically stable and,moreover,for everyε∈(0,1),there exists aδ0=δ0(ε)＞0 such that

whenever

LetC1,2(R+×Rn;R+)denote the family of non-negative functionsV(t,x)defi ned on R+×Rn,which are once continuously diff erentiable intand twice continuously diff erentiable inx.

Defi ne an operatorLacting onC1,2(R+×Rn;R+)functions by

whereVx=(Vx1,···,Vxn)andVxx=(Vxixj)n×n.Moreover,letKdenote the family of all continuous nondecreasing functionsρ:R+→R+such thatρ(0)=0 andρ(r)＞0,ifr＞0.

Lemma3.1[16]AssumethatthereexistV∈C1,2(R+×Rn;R+)andρ1,ρ2,ρ3∈Ksuchthat

and

Thenthezerosolutionforthestochasticdifferentialequationisstochasticallyasymptotically stable.

Now we present the main stability results of(1.1)and(1.2).

Theorem3.1Supposethatthereexistpositiveconstantsa1,b1,b2,c1,σ1,α1,α2,β1,γ1andMsuchthat:

(iv)

(v)

(vi)

Theorem3.2SupposethatthereexistpositiveconstantsL andHsuchthat:

4 Proof of Theorem 3.1

We write equation(1.1)in the following equivalent system

Define a Lyapunov functionalas

wherext=x(t+s),s≤0 andδis a positive constant,which will be determined in the following proof.

Thus from(4.2),(4.1)and by Itˆo formula,we get

From conditions(i)and(ii)of Theorem 3.1 we haveandThen by substituting them into(4.3)we obtain

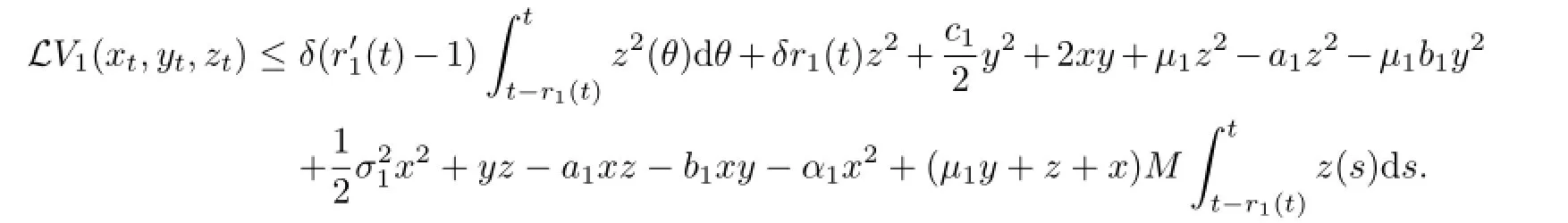
Now from condition(iii)of Theorem 3.1 we have

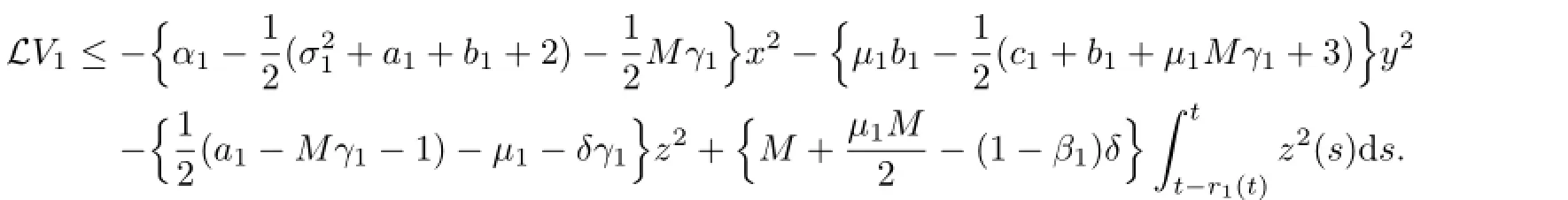
If we take

then

Therefore,if

we have

Hence we can get

Therefore from(4.4),(4.5)and(4.6),all the assumptions of Lemma 3.1 are satisfi ed,so the zero solution for(1.1)is stochastically asymptotically stable.This completes the proof of Theorem 3.1.

5 Proof of Theorem 3.2

Equation(1.2)has the following equivalent system

Define a Lyapunov functionalas

whereλis a positive constant,which will be determined below.Thus from(5.2)and(5.1), byformula,we get

From conditions(i),(ii),(iv),(viii)and(ix)of Theorem 3.2 we have-f3(x)≤-α3x,ΔandThen by substituting them into(5.3)we obtain

Thus from condition(iii)of Theorem 3.2,we have

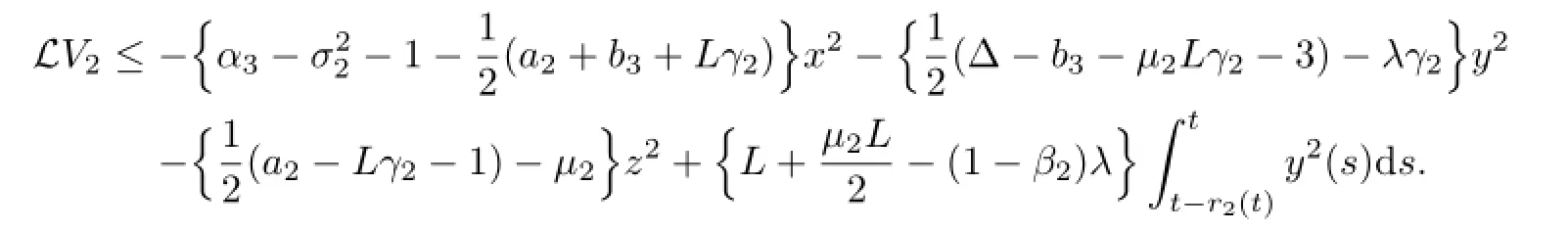
If we take

then

Therefore,if

then we can get

Then we have

Therefore from(5.4),(5.5)and(5.6),all the assumptions of Lemma 3.1 are satisfied.Thus the proof of Theorem 3.2 is now complete and the zero solution for(1.2)is stochastically asymptotically stable.

6 Conclusion

If we allow for some randomness in some of the coeffi cients of a diff erential equation we often obtain a more realistic mathematicalmodelof the situation.So the study of stochastic systems is therefore much richer than the classicaldeterministic ones.Based on constructing Lyapunov functionals,suffi cient conditions for the stochastic asymptotic stability of the zero solution for the third-order nonlinear stochastic delay diff erential equations(1.1)and(1.2) are established.The obtained results extend existing results in the literature on deterministic systems(e.g.see[21,23-25,28])to stochastic systems.The mathematical techniques employed here are very much diff erent from the previous ones.

[1]A.M.A.Abou-El-Ela,A.I.Sadek,A.M.Mahmoud and R.O.A.Taie,On the stochastic stability and boundedness of solutions for stochastic delay diff erential equation of the second-order,Chin.J.Math.,2015(2015),1-8.

[2]A.M.A.Abou-El-Ela,A.I.Sadek and A.M.Mahmoud,On the stability of solutions for centain second-order stochastic delay diff erential equations,DifferentialEquationsandControl Processes,2(2015),1-13.

[3]O.Arino,M.L.Hbid and E.Ait Dads,Delay Diff erential Equations and Application,Springer, 2006.

[4]T.D.Frank and P.J.Beek,Stationary solutions of linear stochastic delay diff erential equations: Applications to biological systems,Phys.Rev.E,64(2001),021917.

[5]J.K.Hale,Theory of Functional Diff erential Equations,Springer-Verlag,New York,1977.

[6]J.K.Hale and S.M.Verduyn Lunel,Introduction to Functional Diff erential Equations,Springer Press,New York,1993.

[7]K.Itˆo and M.Nisio,On stationary solutions of a stochastic diff erential equations,J.Math. KyotoUniv.,4(1964),1-75.

[8]A.F.Ivanov,Y.I.Kazmerchuk and A.V.Swishchuk,Theory,stochastic stability and applications of stochastic delay diff erential equations:A survey of results,DifferentialEquations DynamicalSystems,11(2003),55-115.

[9]R.Z.Khasminskii and V.B.Kolmanovski,Stability of delay stochastic equations,TheoryProbab.Math.Stat.,Kiev,2(1970),111-120.

[10]V.Kolmanovskii and A.Myshkis,Introduction to the Theory and Applications of Functional Diff erential Equations,Kluwer Academic,Dordrecht,1999.

[11]V.Kolmanovskii and L.Shaikhet,About some features of general method of Lyapunov functionals construction,SACTA,6:1(2004),49-76.

[12]H.Kushner,On the stability ofprocesses defi ned by stochastic diff erence-diff erential equations,J.DifferentialEquations,4(1968),424-443.

[13]S.Li and L.Wen,Functional Diff erential Equations,Changsha:Human Science and Technology Press,1987.

[14]V.Mandrekar,On Lyapunov stability theorems for stochastic(deterministic)evolution equations,Stoch.Anal.Appl.inPhysics,(1994),219-237.

[15]X.Mao,Existence and uniqueness of solutions of stochastic integral equations,J.ofFuzhou Univ.,4(1983),41-50.

[16]X.Mao,Stochastic Diff erential Equations and Their Applications,Horwood Publishing,Chichester,UK,1997.

[17]X.Mao,Attraction,stability and boundedness for stochastic diff erentialdelay equations,NonlinearAnalysis,47(2001),4795-4806.

[18]X.Mao and A.Shah,Exponentialstability ofstochastic diff erentialdelay equations,Stochastics andStochasticReports,60:1-2(1997),135-153.

[19]X.Mao,C.Yuan and J.Zou,Stochastic diff erential delay equations of population dynamics,J.Math.Anal.Appl.,304:1(2005),296-320.

[20]S.-E.A.Mohammed,Stochastic Functional Diff erential Equations,Research Notes in Mathematics 99,Pitman Advanced Publishing Program,Boston-London-Melbourne,1984.

[21]B.S.Ogundare,On boundedness and stability of solutions of certain third-order delay diff erential equation,J.NigerianMathematicalSociety,31(2012),55-68.

[22]B.Oksendal,Stochastic Diff erential Equations(An Introduction with Applications),Springer-Verlag,Heidelberg-New York,2000.

[23]A.I.Sadek,Stability and boundedness of a kind of third-order delay diff erentialsystem,Applied MathematicsLetters,16(2003),657-662.

[24]A.I.Sadek,On the stability of solutions of some non-autonomous delay diff erential equations of the third-order,AsymptoticAnalysis,43(2005),1-7.

[25]P.Shekhar,V.Dharmaiah and G.Mahadevi,Stability and boundedness of solutions of delay diff erential equations of third-order,IOSRJournalofMathematics,5:6(2013),9-13.

[26]R.Wu and X.Mao,Existence and uniqueness of solutions of stochastic diff erential equations,Stochastics,11(1983),19-32.

[27]F.Wu and S.Hu,Attraction,stability and robustness for stochastic functional diff erential equations with infinite delay,Automatica,47(2011),2224-2232.

[28]Y.F.Zhu,On stability,boundedness and existence of periodic solution of a kind of third-order nonlinear delay diff erential system,Ann.ofDiff.Eqs.,8:2(1992),249-259.

(editedbyLiangweiHuang)

∗Manuscript received May 25,2015;Revised August 3,2015