IMPROVED FRACTIONAL SUB-EQUATION METHOD AND ITS APPLICATIONS TO FRACTIONAL PARTIAL DIFFERENTIAL EQUATIONS∗†

Guoying Xu,Tiecheng Xia

(Dept.ofMath.,ShanghaiUniversity,Shanghai200444)

IMPROVED FRACTIONAL SUB-EQUATION METHOD AND ITS APPLICATIONS TO FRACTIONAL PARTIAL DIFFERENTIAL EQUATIONS∗†

Guoying Xu,Tiecheng Xia‡

(Dept.ofMath.,ShanghaiUniversity,Shanghai200444)

Based on an improved fractional sub-equation method involving Jumarie’s modified Riemann-Liouville derivative,we construct analytical solutions of space-time fractional compound KdV-Burgers equation and coupled Burgers’equations.These results not only reveal that the method is very eff ective and simple in studying solutions to the fractional partial diff erential equation,but also include some new exact solutions.

improved fractionalsub-equation method;modifi ed Riemann-Liouville derivative;fractional diff erential equation;compound KdV-Burgers equation;coupled Burgers’equations

2000MathematicsSubjectClassification35C07;35C08;35P99

1 Introduction

Fractional diff erentialequations(FDEs)are generalizations of classical diff erential equations of integer order.In recent decades,fractional diff erential equations have been investigated by many scholars due to their frequent appearances in various applications such as in physics,biology,engineering and so on[1-7].Many authors have investigated some aspects of fractional diff erentialequations,such as the existence and uniqueness of solutions of the Cauchy-type problems,the methods for explicit and numerical solutions,the integrable coupling system of the fractional soliton equation[8,9].Among the investigations for fractional diff erential equations,the research for seeking exact solutions and numerical solutions of fractional diff erential equations is an important topic,and many powerful and effi cient methods have been proposed,such as the adomian decomposition method[10], the variational iterative method[11],the diff erential transformation method[12],and the fractional Riccati subequation method[18,19].

The rest of this paper is organized as follows.In Section 2,some basic definitions of Jumarie’s modified Riemann-Liouville derivative and the main steps of the improved fractional sub-equation method are given.In Section 3,we construct the exact solutions of space-time fractional compound KdV-Burgers equation and coupled Burgers’equations via the method.Some conclusions and discussions are given in Section 4.

2 Preliminaries

2.1Jumarie’smodifiedRiemann-Liouvillederivative

The Jumarie’s modifi ed Riemann-Liouville derivative of orderαis defi ned by the following expression[22,23]

Some properties for the proposed modified Riemann-Liouville derivative were listed in[20] as follows

2.2Descriptionofimprovedfractionalsub-equationmethod

The essential steps of improved fractional sub-equation method are described as follows:

Step 1Suppose that a nonlinear FDEs,with two independent variablesxandt,is given by

Step 2Through the traveling wave transformation

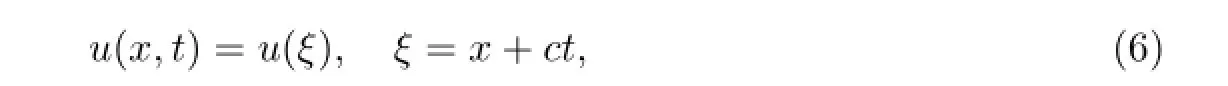
eqution(5)is reduced to the following nonlinear fractional ordinary diff erential equations (FODEs)

where the prime“′”denotes the derivation with respect toξ,andcis a constant to be determined below.If possible,we should integrate equation(7)term by term one or more times.

Step 3Suppose that solutions of equation(7)can be expressed by a polynomial inφ(ξ) as follows

whereai(i=-m,···,m)are constants to be determined below.The positive integermcan be determined by the homogeneous balance between the highest order derivatives and the nonlinear terms appearing in(7).Andφ=φ(ξ)satisfi es the following fractional Riccati equation

whereσis a constant.Zhang et al.[24]first obtained the following solutions of the fractional Riccati equation(9)

with the generalized hyperbolic and trigonometric function

Step 4Substituting(8)along with(9)into(7)by the properties of Jumarie’s modified Riemann-Liouville derivative(2)-(4),we can get a polynomial inφ(ξ).Setting all the coeffi cients ofφ(ξ)k(k=···,-1,0,1,···)to be zero,we can yields a set of over-determined nonlinear algebraic equations forc,ai(i=-m,···,m).

Step 5Assume that the constantsc,ai(i=-m,···,m)can be obtained by solving the algebraic equations in Step 4.Substituting these constants and the solutions of(10)into (8),then we can obtain the explicit solutions of equation(5).

3 Applications

3.1Space-timefractionalcompoundKdV-Burgersequation

Many researchers have studied the compound KdV-Burgers equation and constructed traveling wave solutions through diff erent methods[25-29].To the best of our knowledge, there is few paper about the space-time fractional compound KdV-Burgers equation.Next, we apply the improved fractional sub-equation method to construct exact traveling wave solutions of a space-time fractional compound KdV-Burgers equation

wherep,q,r,sare constants.This system of equation involving nonlinear,dispersion and dissipation eff ect,can be seen as a compound equation of the fractional KdV,mKdV and Burgers equations.

(1)Whenr=0 andp,q,s/=0,(12)becomes the following space-time fractional compound KdV equation

(2)Whenp=0 andq,r,s/=0,(12)becomes the following space-time fractional mKdVBurgers equation

(3)Whenq=0 andp,r,s/=0,(12)becomes the following space-time fractional KdVBurgers equation

(4)Ifp,r=0 andq,s/=0,(12)becomes the following space-time fractional mKdV equation

Considering the traveling wave transformationsu=u(ξ)andξ=x+ct,(12)can be reduced to the following nonlinear FODE

Substituting(18)along with(9)into(17)and setting the coeffi cients ofφ(ξ)to be zero, we obtain a set of algebraic equations aboutc,a-1,a0,a1.Solving the algebraic equations by Maple,we get the results as follows.

We supposeσ,p,q,randsare free parameters.

Case 3.1.1

Case 3.1.2

Case 3.1.3

Using Case 3.1.3,equations(18)and(10),we can obtain the following exact solutions of equation(12)

Using Cases 3.1.2 and 3.1.3,we could obtain more exact solutions of equation(12),and here we do not list all of them.

Remark1Through the improved fractional sub-equation method,the exact solutions of equations(13),(14)and(16)are the particular cases of the solutions of equation(l2).

Remark2In the above three cases,if we setα=1,the above three family solutions is exactly the classical compound KdV-Burgers equations in[28].

3.2Space-timefractionalcoupledBurgers’equations

System of coupled Burgers equations is a simple model of sedimentation or evolution of scaled volume concentrations of two kinds of particles in fl uid suspensions or colloids, under the eff ect of gravity.It has been studied by many authors by diff erent methods [30-33].Especially recently,Dehghan obtained a good numerical results using Adomian-Pade technique[33].However,to the best of our knowledge,the study for the time-space fractional coupled Burgers equations of the following form derived by Esipov[31]has not been investigated through fractional sub-equation method.

Space-time-fractional coupled Burgers’equations {

The constantsp,qdepend on the parameters of the system such as the Peclet number,the Stokes velocity of particles due to gravity,and the Brownian diff usivity.In the case ofα=1, equation(27)reduces to the classical coupled Burgers’equations.

The same procedure as illustrated in Section 3.1,we suppose the solutions can be expressed by a polynomial inφas follows {

Substituting(29)along with(9)into(28)and then setting the coeffi cients ofφ(ξ)to be zero,we can obtain a set of algebraic equations about.Solving the algebraic equations by Maple,we get the results as follows.

Case 3.2.1

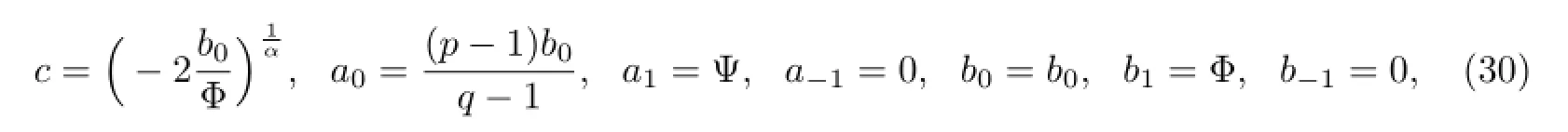
Case 3.2.2

Case 3.2.3

Using Case 3.2.3,(29)and(10),we can find the following exact solutions of(27)

4 Conclusion

In this paper,as applications of the improved fractional sub-equation method,some exact analytical solutions of the space-time fractional compound KdV-Burgers equation and coupled Burgers’equations are obtained successfully.These solutions include generalized hyperbolic function solutions,generalized trigonometric function solutions and rational function solutions,which may be useful to further study the mechanisms of the complicated nonlinear physical phenomena and FDEs.

From our results obtained in this paper,we conclude that the improved fractional subequation method is powerful,eff ective and convenient for nonlinear FDEs.

APPENDIXBekir and G¨uner[34]studied space-time fractional coupled Burgers’equations:

when

when

when

[1]A.Kilbas,H.M.Srivastava,J.J.Trujillo,Theory and applications of fractional diff erential equations,North-HollandMathematicsStudies,Elsevier Science,Amsterdam,the Netherlands,204(2006),1-523.

[2]R.Hilfer,Applications of Fractional Calculus in Physics,World Scientifi c Publishing,River Edge,NJ,USA,2000.

[3]B.J.West,M.Bologna,P.Grigolini,Physics of Fractal Operators,Springer,New York,NY, USA,2003.

[4]K.S.Miller,B.Ross,An Introduction to the Fractional Calculus and Fractional Diff erential Equations,John Wiley Sons,New York,NY,USA,1993.

[5]S.G.Samko,A.A.Kilbas,O.I.Marichev,Fractional Integrals and Derivatives,Gordon and Breach Science,Yverdon,Switzerland,1993.

[6]I.Podlubny,Fractional Diff erential Equations,Mathematics in Science and Engineering,Academic Press,San Diego,Calif,USA.1999,198.

[7]K.B.Oldham,J.Spanier,The Fractional Calculus,Academic Press,New York,NY,USA, 1974.

[8]Fajun Yu and Hongqing Zhang,A new fractional order soliton equation hierarchy and its integrable coupling system,Appl.Math.andComput.,194(2007),259-266.

[9]Fajun Yu,Integrable coupling system of fractional soliton equation hierarchy,Phys.Lett.A.,373(2009),3730-3733.

[10]A.M.A.El-Sayed and M.Gaber,The Adomian decomposition method for solving partial differential equations of fractal order in fi nite domains,Phys.Lett.A.,359(2006),175-182.

[11]J.He,Anew approach to nonlinear partialdiff erentialequations,CommunicationsinNonlinear ScienceandNumericalSimulation,2(1997),230-235.

[12]Z.Odibat and S.Momani,A generalized diff erential transform method for linear partial diff erential equations of fractional order,Appl.Math.Lett.,21(2008),194-199.

[16]Z.-B.Li,J.-H.He,Fractional complex transform for fractional diff erential equations,Math. Comput.Appl.,15(2010),970-973.

[17]Z.-B.Li,J.-H.He,Application of the fractional complex transform to fractional diff erential equations,NonlinearSciLett.,2A(2011),121-126.

[18]S.Zhang,H.Q.Zhang,Fractional sub-equation method and its applications to nonlinear fractional PDEs,Phys.Lett.A.,375(2011),1069-1073.

[19]S.M.Guo,L.Q.Mei,Y.Li,The improved fractional sub-equation method and its applications to the space-time fractional diff erential equations in fluid mechanics,Phys.Lett.A.,376(2012),407-411.

[20]B.Lu,B¨acklund transformation of fractional Riccati equation and its applications to nonlinear fractional partial diff erential equations,Phys.Lett.A.,376(2012),2045-2048.

[21]M.L.Wang,Solitary wave solutions for variant Boussinesq equations,Phys.Lett.A.,199(1995),169-172.

[22]G.Jumarie,Modified Riemann-Liouville derivative and fractional Taylor series of nondiff erentiable functions further results,Math.Appl.,51(2006),1367-1376.

[23]G.Jumarie,Cauchy’s integral formula via the modifi ed Riemann-Liouville derivative for analytic functions of fractional order,Appl.Math.Lett.,23(2010),1444-1450.

[24]S.Zhang,Q.A.Zong,D.Liu,Q.Gao,A generalized exp-function method for fractional Riccati diff erential equations,Commun.Fract.Calc.,1(2010),48-51.

[25]X.D.Zheng,T.C.Xia,H.Q.Zhang,New exact traveling wave solutions for compand KdVBurgers equation in mathematical physics,Appl.Math.E-Notes,2(2002),45-50.

[26]X.Liu and W.Zhang,Appl.Math.Sci.,4(2010),959-972.

[27]L.Gong and J.Pan,Some new solitary wave solutions to a compound KdV-Burgers equation,Commun.Theor.Phys.,50(2008),51-52.

[29]M.L.Wang,Exact solutions for a compound KdV-Burgers equation,PhysicsLettersA.,213(1996),279-287.

[30]J.Nee,J.Duan,Limit set of trajectories of the coupled viscous Burger’s equations,Appl. Math.Lett.,11(1998),57-61.

[31]S.E.Esipov,Coupled Burgers equations:a model of polydispersive sedimentation,Phys.Rev. E.,52(1995),3711-3718.

[32]M.A.Abdoua,A.A.Solimanb,Variational iteration method for solving Burger’s and coupled Burger’s equations,J.Comput.Appl.Math.,181(2005),245-251.

[33]Mehdi Dehghan,Asgar Hamidi,Mohammad Shakourifar,The solution of coupled Burger’s equations using Adomian-Pade technique,Appl.Math.Comput.,189(2007),1034-1047.

[35]Fajun Yu and Hongqing Zhang,A new fractional order soliton equation hierarchy and its integrable coupling system,Appl.Math.andComput.,194(2007),259-266.

[36]Fajun Yu,Integrable coupling system of fractional soliton equation hierarchy,Phys.Lett.A.,373(2009),3730-3733.

[37]A.M.A.El-Sayed and M.Gaber,The Adomian decomposition method for solving partial differential equations of fractal order in finite domains,Phys.Lett.A.,359(2006),175-182.

[38]J.He,Anew approach to nonlinear partialdiff erentialequations,CommunicationsinNonlinear ScienceandNumericalSimulation,2(1997),230-235.

[39]Z.Odibat and S.Momani,A generalized diff erential transform method for linear partial diff erential equations of fractional order,Appl.Math.Lett.,21(2008),194-199.

(editedbyLiangweiHuang)

∗This work was partially supported by the Natural Science Foundation of China(No.11271008).

†Manuscript received March 17,2015;Revised May 9,2015

‡Corresponding author.E-mail:xiatc@shu.edu.cn