GLOBAL BLOW-UP FOR A DEGENERATE AND SINGULAR NONLOCAL PARABOLIC EQUATION WITH WEIGHTED NONLOCAL BOUNDARY CONDITIONS∗†

Xingying LiuBaozhu ZhengYoupeng Chen

(1.Dept.ofMath.,QinghaiNormalUniversity,Xining810008;

2.SchoolofMath.andStatistics,YanchengNormalUniversity,Yancheng224002,Jiangsu)

GLOBAL BLOW-UP FOR A DEGENERATE AND SINGULAR NONLOCAL PARABOLIC EQUATION WITH WEIGHTED NONLOCAL BOUNDARY CONDITIONS∗†

Xingying Liu1,2,Baozhu Zheng1,2,Youpeng Chen2‡

(1.Dept.ofMath.,QinghaiNormalUniversity,Xining810008;

2.SchoolofMath.andStatistics,YanchengNormalUniversity,Yancheng224002,Jiangsu)

This paper deals with the blow-up properties of positive solutions to a degenerate and singular nonlocal parabolic equation with weighted nonlocalboundary conditions. Under appropriate hypotheses,the globalexistence and fi nite time blow-up of positive solutions are obtained.Furthermore,by using the properties of Green’s function,we find that the blow-up set of the blow-up solution is the whole domain(0,a),and this diff ers from parabolic equations with local sources case.

degenerate and singular parabolic equation;weighted nonlocal boundary condition;global existence;fi nite time blow-up;Green’s function

2000MathematicsSubjectClassification35K57;35K60;35K65

1 Introduction

In this paper we consider the following degenerate and singular nonlocal parabolic equation with weighted nonlocal boundary conditions

whereq,αandaare constants withq≥0,0≤α＜1 anda＞0,g(x)andh(x)are nonnegative continuous on[0,a]and not identical to zero.It is necessary to point out that problem(1.1)is degenerate and singular because the coeffi cients ofut,uxxanduxtend to 0 and∞asx→0,respectively.

Early in 1979,Ockendon in[1]established the following famous Ockendon’s modelwhich describes the flow in a channel of a fl uid whose viscosity is temperature dependent

whereurepresents the temperature of the fluid.Obviously,the coeffi cientxofutmay tend to 0,we can regard equation(1.2)as degenerate.From then on,Floater in[2]and Chan and Liu in[4]approximated the reaction term euwithup,and investigated the blow-up properties of the following problem

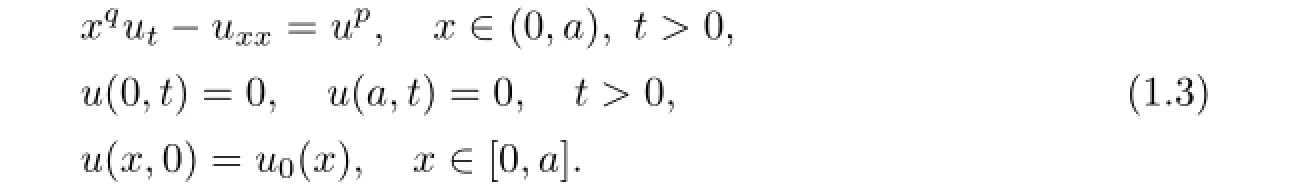
They pointed out that for the case of 1＜p≤q+1,if the solutionu(x,t)to problem(1.3) blows up in fi nite time,then it blows up at the boundary.This contrasts with a result of Friedman and Mcleod[3],who showed that for the caseq=0,the blow-up set of the solution to problem(1.3)is a proper compact subset of(0,a).Recently,Chen,Liu and Xie in[5] investigated the following degenerate and singular parabolic equation with nonlocal source

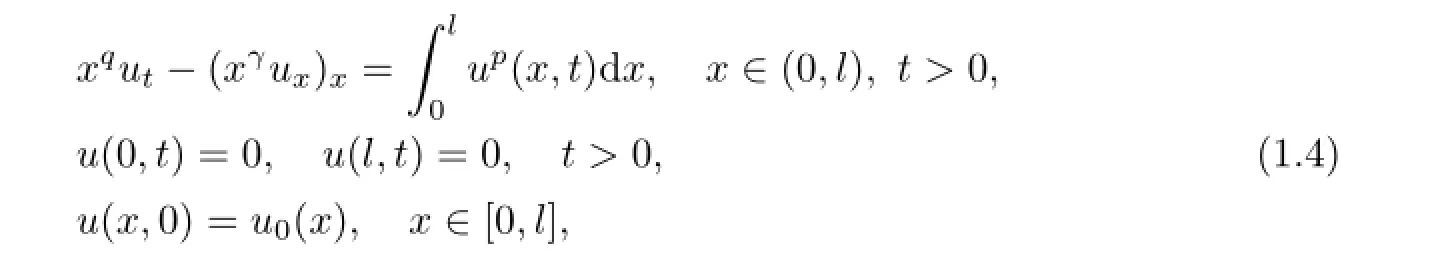
wherethey proved that the blow-up set is the whole domain, and this diff ers from the parabolic equation with local source case.

On the other hand,parabolic equations with nonlocal boundary conditions come from applied science,for instance,in the study of the heat conduction with thermoelasticity, Day in[6,7]derived a class of heat equations with nonlocal boundary conditions in onedimensional space.In this model,the solutionu(x,t)describes the entropy of per volume of the material.Motivated by the works of Day,many scholars have devoted to studying the blow-up behaviour of diff erent kinds of parabolic equations with nonlocal boundary conditions in the past few years,see[8-15]and the references therein.

The main goal of this paper is to investigate the eff ects ofαandq,and the weighted functionsg(x)andh(x)in problem(1.1)on the global existence and blow-up singularity of solutions.Compared with[11],we need more skills to handle the diffi culties,which are produced by the degeneracy and singularity of problem(1.1).Before stating our results,we make some assumptions on the weight functionsg(x),h(x)and the initial datumu0(x).

(H1)g(x)andh(x)are continuous,nonnegative and not identical to zero on[0,a].

(H2)for someγ∈(0,1),u0(x)＞0 in(0,a),∫and

(H3)

Our main results are as follows.

Theorem1.1Assumethat(H1),(H2)and(H3)hold,andthatandthenthesolutionu(x,t)toproblem(1.1)existsgloballyifu0(x)issufficientlysmallandf(0)=f′(0)=0.

Theorem1.3Assumethat(H1)-(H4)hold,thenthesolutionu(x,t)toproblem(1.1)blowsupinfinitetimeprovidedthatu0(x)issufficientlylarge.

Theorem1.4Assumethat(H1)-(H4)hold,andthatthereexisttwopositiveconstants k0andpwithp＞2suchthatf(s)≥k0spforalls≥0,ifthesolutionu(x,t)toproblem(1.1)blowsupinfinitetimeatsomepointin(0,a),thentheblow-upsetofu(x,t)isthe wholedomain(0,a).

This paper is organized as follows.In Section 2,we show the comparison principle and the local existence.In Section 3,some suffi cient conditions for the existence of global solution or fi nite time blow-up solutionu(x,t)to problem(1.1)are given.In Section 4,we show the set of the bow-up solution to problem(1.1)is the whole domain(0,a).

2 The Comparison Principle and the Local Existence

Lemma2.1Assumethatandsatisfies

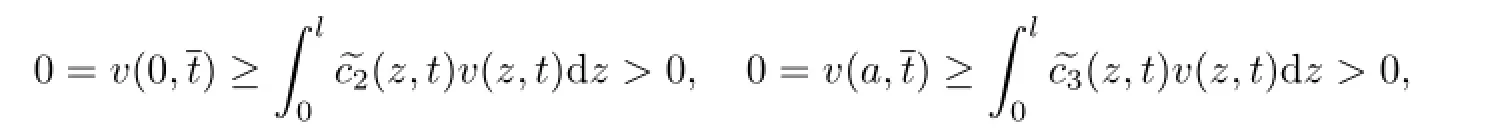
which also lead to a contradiction.And then we haveonThis ends the proof of Lemma 2.1.

In order to get the global existence and finite time blow-up results for problem(1.1),we need yet the following comparison principle which is a direct consequence of Lemma 2.1.

The local existence of the positive classical solution to problem(1.1)can be obtained by the regularization method,the representation formula and fi xed point theorem as in[5,17], then we have the following theorem.

Theorem2.1Assumethat(H1)-(H3)hold,thenthereexistapositivetimeT∗(T∗≤+∞)andsuchthatu(x,t)isthemaximalintimesolutiontoproblem(1.1).IfT∗＜+∞,thenwehave

The proof is more or less standard,and is therefore omitted here.

3 Global Existence and Finite Time Blow-up

In this section,fi rst of all,by constructing some appropriate global supersolutions,and employing the comparison principle,we obtain the global existence result for problem(1.1), and give the proof of Theorem 1.1.

ProofofTheorem1.1Consider the following boundary value problem for ordinary diff erential equation

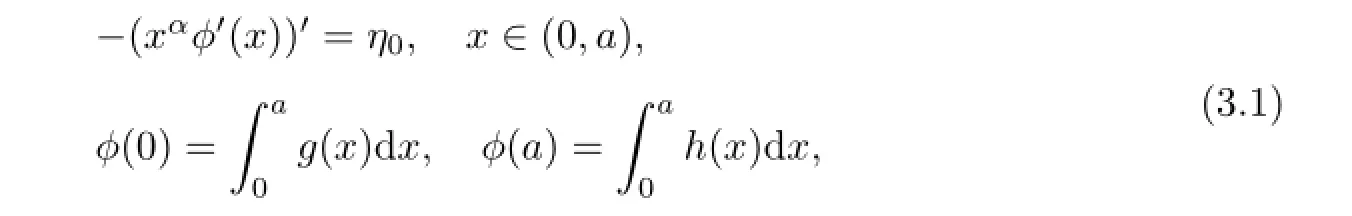
whereη0is a positive constant to be fi xed below.We can easily solve this problem,and obtain its solution

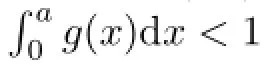
In virtue of the conditionf(0)=f′(0)=0,it follows from L’Hospital role that

Then we can choose a positive constantb0such that

The above inequalities show thatv1(x,t)is a global supersolution to problem(1.1),and therefore Lemma 2.2 implies that the solutionu(x,t)to problem(1.1)exists globally.This completes the proof.

Next,we discuss the blow-up singularity for problem(1.1)and give the proofs of Theorems 1.2 and 1.3.

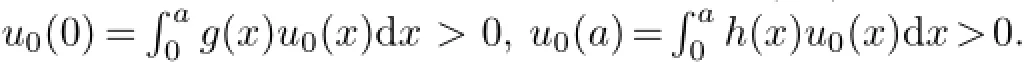
In virtue of hypothesis(H3)and the theory of ordinary diff erential equations,there exists a unique solutions(t)to problem(3.4),which is increasing.Utilizing hypothesis(H4),if we denote its maximal existence time bythen

Setv2(x,t)=s(t),then

therefore from the above inequalities,v2(x,t)is the subsolution to problem(1.1).Then Lemma 2.2 implies that the solutionu(x,t)to problem(1.1)satisfiesu(x,t)≥v2(x,t)forx∈[0,a],t＞0.And thereforeu(x,t)blows up in fi nite time,and this completes the proof.

Letµ1be the fi rst eigenvalue andξ(x)be the corresponding eigenfunction ofthe following eigenvalue problem

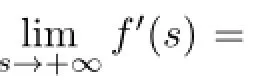
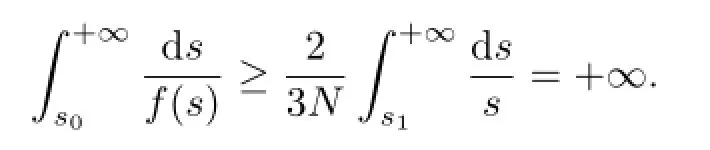
because ofξx(a)≤0.Noting thatfis convex,and using Jensen’s inequality,we have

Using the conditionf′(s)＞0 in(0,+∞)in(H3)and noticing that

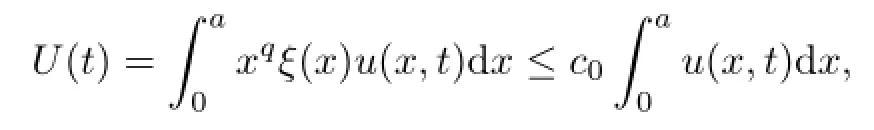
we obtain

If we chooseu0(x)suffi ciently large such that

then from(3.8)we obtain

If we denote the maximal existence time ofU(t)by,then

HenceU(t)tends to infinity in finite time.Therefore the solutionu(x,t)to problem(1.1) blows up in fi nite time.And the proof of Theorem 1.3 is completed.

4 Global Blow-up

In this section,we discuss the blow-up set of the blow-up solution to problem(1.1),and give the proof of Theorem 1.4.From Theorems 1.2 and 1.3,we see that the solutionu(x,t) to problem(1.1)blows up in fi nite time for large initial data.We denote byTthe blow-up time of the blow-up solutionu(x,t)to problem(1.1).Chan and Chan in[20]showed that the Green’s functionG(x,ξ,t-τ)associated with the operator,subjected to the first boundary conditions exists.In order to get the global blow-up result,we transfer problem(1.1)by the following transformations

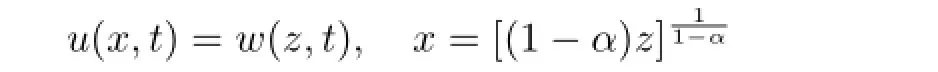
to a new problem

For convenience we state Lemmas 2 and 4 in[20]in the following lemma.

Lemma4.1TheGreen’sfunctionG(x,ξ,t-τ)satisfies:

(a)Fort＞τ,G(y,ξ,t-τ)iscontinuousfor(y,t,ξ,τ)∈([0,l]×(0,T])×((0,l]×[0,T)).

(b)Foreachfixed(ξ,τ)∈(0,l]×[0,T),Gt(y,ξ,t-τ)∈C([0,l]×(τ,T]).

(c)In{(y,t,ξ,τ):xandξarein(0,l),T≥t≥τ≥0},G(y,ξ,t-τ)ispositive.

Similarly to the proof of Lemma 7 in[21],we can easily show the following additional properties ofG(x,ξ,t-τ).

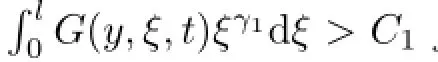
Now,we can show the global blow-up result.

Theorem4.1Ifthesolutionv(y,t)to(4.2)blowsupinfinitetimeTandatthepoint y0∈(0,l),thentheblow-upsetofv(y,t)isthewholedomain(0,l).

ProofBy Green’s second identity,Lemmas 4.1 and 4.2,we have for(y,t)∈(0,l)×(0,T)On the other hand,assume thatis the Green’s function associated with the operatorsubjected to homogenous boundary condition,then we have fort＞τ,

And we easily obtain from[22]that

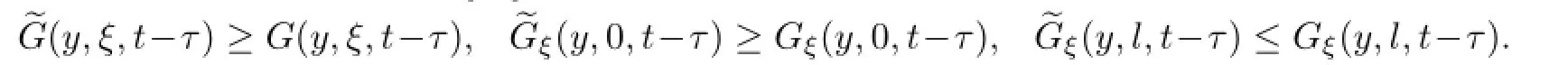
Then by using Holder’s inequality and Lemma 4.2,we obtain

or

ProofTheorem1.4From the above two transformations and Theorem 4.1,if the solutionu(x,t)to(1.1)blows up in fi nite time at some point in(0,a),then the blow-up set ofu(x,t)is the whole domain(0,a).And the proof of Theorem 1.4 is completed.

[1]H.Ockendon,Channel fl ow with temperature-dependent viscosity and internal viscous dissipation,J.FluidMech.,93(1979),737-746.

[2]M.S.Floater,Blow-up at the boundary for degenerate semilinear parabolic equations,Arch. RationalMech.Anal.,114(1991),57-77.

[3]A.Friedman and B.Mcleod,Blow-up of positive solutions of semilinear heatequations,Indiana Univ.Math.J.,34(1985),425-447.

[4]C.Y.Chan,H.T.Liu,Global existence of solutions for degenerate semilinear parabolic equations,NonlinearAnal.,34(1998),617-628.

[5]Y.P.Chen,Q.L.Liu,C.H.Xie,Blow-up for degenerate parabolic equation with nonlocalsource,Proc.Amer.Math.Soc.,132(2004),135-145.

[6]W.A.Day,Extensions ofproperty of heat equation to linear thermoelasticity and other theories,Quart.Appl.Math.,40(1982),319-330.

[7]W.A.Day,A decreasing property of solutions of parabolic equations with applications to thermoelasticity,Quart.Appl.Math.,40(1983),468-475.

[8]A.Friedman,Monotonic decay of solutions of parabolic equations with nonlocal boundary conditions,Quart.Appl.Math.,44(1986),401-407.

[9]K.Deng,Comparison principle for some nonlocalproblems,Quart.Appl.Math.,50(1992),517-522.

[10]S.Seo,Blowup of solutions to heat equations with nonlocal boundary conditions,KobeJ. Math.,13(1996),123-132.

[11]Z.G.Lin,Y.R.Liu,Uniform blow-up pro.les for diff usion equations with nonlocal source and nonlocal boundary,ActaMath.Sci.,24B(2004),443-450.

[12]Y.Wang,C.Mu,Z.Xiang,Blow up of solutions to a porous medium equation with nonlocal boundary condition,Appl.Math.Comput.,192(2007),579-585.

[13]Z.Cui,Z.Yang,Roles ofweight functions to a nonlinear porous medium equation with nonlocal source and nonlocal boundary condition,J.Math.Anal.Appl.,342(2008),559-570.

[14]Y.Z.Gao,W.J.Gao,Existence and blow-up of solutions for a porous medium equation with nonlocal boundary condition,Appl.Anal.,90(2011),799-809.

[15]Y.P.Chen,L.H.Liu,The blow-up profi le for a nonlocal nonlinear parabolic equation with a nonlocal boundary condition,Quart.Appl.Math.,LXX:4(2012),759-772.

[16]A.Friedman,Partial Diff erential Equations of Parabolic Type,Prentice-Hall,Inc.Englewood Cliff s.NJ,1964.

[17]Y.F.Yin,On nonlinear parabolic equations with nonlocal boundary condition,J.Math.Anal. Appl.,185(1994),54-60.

[18]Lawrence C.Evans,Partial Diff erential Equations,American Mathematical Society,Providence,Rhode Island,1998.

[19]N.W.Mclachlan,Bessel Functions for Engineers,2nd Edition,Oxford at the Clarendon Press, London,1955.

[20]C.Y.Chan,W.Y.Chan,Existence of classical solutions for degenerate semilinear parabolic problems,Appl.Math.Comput.,101(1999),125-149.

[21]C.Y.Chan,J.Yang,Complete blow up for degenerate semilinear parabolic equations,J. Comput.Appl.Math.,113(2000),353-364.

[22]C.Y.Chan,W.Y.Chan,Complete blow-up of solutions for degenerate semilinear parabolic fi rst initial-bountray value problems,Appl.Math.Comput.,177(2006),777-784.

(editedbyLiangweiHuang)

∗This research was supported partially by the foundation of professors and doctors of Yancheng Normal University(14YSYJB0106)and by the research scheme of the natural science of the universities of Jiangsu Province(08KJD110017 and 13KJB110028).

†Manuscript received January 27,2015;Revised May 30,2015

‡corresponding author.E-mail:youpengc123@aliyun.com