最小二乘支持向量机在堆芯功率分布重构中的应用

彭星杰，李天涯，李 庆，王 侃

(1.清华大学 工程物理系，北京 100084；2.中国核动力研究设计院 核反应堆系统设计技术重点实验室，四川 成都 610041)



最小二乘支持向量机在堆芯功率分布重构中的应用

彭星杰1,2，李天涯2，李 庆2，王 侃1

(1.清华大学 工程物理系，北京 100084；2.中国核动力研究设计院 核反应堆系统设计技术重点实验室，四川 成都 610041)

应用最小二乘支持向量机(LS-SVM)进行了堆芯轴向功率分布重构的研究，通过6节堆内中子探测器的信号重构出堆芯轴向18个节块的功率。使用ACP-100模块式小堆的7 740套轴向功率分布对LS-SVM重构算法进行了验证，实验结果表明：LS-SVM算法的重构精度远优于交替条件期望(ACE)算法，且LS-SVM算法具有良好的鲁棒性。

最小二乘支持向量机；功率分布重构；鲁棒性

堆芯功率分布在线监测对保证反应堆的安全运行起到了至关重要的作用，大部分的反应堆都安装有堆内中子探测器或堆外中子探测器来进行堆芯功率分布监测。在线监测系统的核心技术之一是堆芯功率分布重构算法，即如何通过探测器信息重构出堆芯功率分布，国内外学者对于这一问题进行了大量工作。基于堆内中子探测器的COLSS系统采用傅里叶拟合算法[1]进行堆芯轴向功率分布的重构，当轴向功率分布为马鞍状或功率分布偏移到堆芯顶端或底端时，傅里叶拟合算法的重构精度较差。傅里叶拟合算法的重构精度强烈依赖于探测器数，而探测器的轴向布置数通常限制在6节以内。为提高轴向功率分布重构精度，Lee等[1]使用交替条件期望(ACE)算法进行了重构方法研究，通过5节堆内中子探测器的读数重构出堆芯轴向20个节块的功率。研究结果表明，ACE算法远优于常规使用的傅里叶拟合算法，ACE算法重构的均方根误差平均值仅为傅里叶拟合算法的35%。

ACE算法属于非线性回归算法的范畴，其他类型的非线性回归算法在核工程领域也得到了应用，其中包括支持向量机(SVM)算法[2-5]。SVM是由Vapnik[6]在统计学习理论的基础上建立起来的一种非线性回归方法，具有自组织、自学习和联想记忆功能。最小二乘支持向量机(LS-SVM)是标准SVM的一个改进，它将SVM中的不等式约束改为等式约束，且将误差平方和损失函数作为训练集的经验损失，提高了求解问题的速度和收敛精度。

本文研究LS-SVM在堆芯轴向功率分布重构中的应用，并将LS-SVM算法与ACE算法进行比较。

1 LS-SVM算法

(1)

其中：φ(x)为输入空间到特征空间的映射；w和b分别为系数向量和偏差项，均为待求量。

未知量通过最优化问题来确定：

(2)

其拉格朗日函数为：

(3)

其中：ei为经验风险因子；αi(i=1,2,…,l)为拉格朗日乘子。

式(3)的Karush-Kuhn-Tucker(KKT)条件为：

(4)

消去式(4)的w和e，可得到：

(5)

其中：y=[y1,y2,…,yl]T；α=[α1,α2,…,αl]T；J=[1,…,1]T；Z=[φ(x1),φ(x2),…,φ(xl)]T；I为单位矩阵。

解这个线性方程组求得b和α，进而求得LS-SVM回归函数：

(6)

使用输入空间的一个核函数k(x,xi)等效高维空间的内积形式，从而回归函数为：

(7)

任意满足Mercer核条件的对称函数均可作为核函数，本文选择径向基核函数作为核函数：

(8)

正则化参数γ和核函数宽度σ在很大程度上决定了LS-SVM的学习和泛化能力。γ影响LS-SVM模型的推广性能，σ影响支持向量数。寻找合适的γ和σ的组合，可使LS-SVM有最好的预测性能。考虑如下的优化问题。

(9)

可以使用优化算法求解最小化问题(式(9))得到最优化的γ和σ。

2 ACE算法

ACE算法[1]是一种估算最佳变换的多元非线性回归方法，其变换结果是使一个随机因变量和多个随机自变量之间具有最大相关系数。对数据列{(yi,x1i,x2i,…,xpi),i=1,…,N}的多元非线性回归问题，ACE算法为：

(10)

(11)

式中：E为数学期望；θ(y)、φj(xj)分别为对变量y、xj所作的变换。

如果对变换后的因变量和自变量总和进行回归分析，则产生误差：

(12)

式(10)和式(11)中的θ(y)、φj(xj)变换是相互耦合的，可令式(13)为最小而进行迭代求解，即求得：

(13)

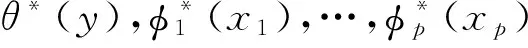
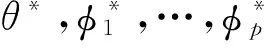
3 回归数据集

利用LS-SVM算法或ACE算法进行轴向功率分布重构，即建立探测器读数Di(i=1,…,M)与节块功率Pj(j=1,…,N)之间的关系，其中M为沿轴向布置的探测器数，N为堆芯沿轴向划分的节块数，在本文中M和N分别设定为6和18。由于LS-SVM算法和ACE算法均为单输出，因而由M个探测器读数估计每一节块功率时，需要训练N个LS-SVM以及迭代得到N套ACE变换。在不影响算法流程与正确性的前提下，为方便起见，本文研究堆芯平均轴向功率分布重构，不针对单一组件。探测器读数由节块功率模拟得到，即从18个节块的功率中均匀地选取6个作为探测器读数。

在进行回归分析，即建立探测器读数与节块功率之间的关系时，可通过堆芯功率能力分析获取大量不同工况下的功率分布。堆芯功率能力分析是研究在确定的反应堆运行模式下堆芯功率分布的控制，以满足核电厂在正常运行工况(Ⅰ类工况)下的电厂机动性要求和非正常工况(Ⅱ类工况)下的安全性要求，本文只考虑Ⅰ类工况。Ⅰ类工况功率能力分析主要验证以下两方面内容：1) 验证由运行图确定的所有Ⅰ类工况状态点均满足LOCA限值要求；2) 验证用于事故分析的参考轴向功率分布包络所有Ⅰ类工况的轴向功率分布。

在进行功率能力分析时，需产生大量覆盖Ⅰ类工况运行图的状态点与相应的全堆功率分布。堆芯的功率分布受到很多因素的影响，在严格遵守技术规格书的限值下，通过改变下列参数可产生大量的堆芯三维功率分布：1) 堆芯功率水平；2) 控制棒组棒位；3) 氙浓度和分布；4) 堆芯燃耗状态。

采用LS-SVM算法和ACE算法时，将功率能力分析产生的样本集数据分为两组，一组为训练集，另一组为验证集。其中训练集从所有样本集中按照堆芯轴向功率上下比均匀抽样，堆芯轴向功率上下比的定义为：

R=PT/PB

(14)

其中，PT、PB分别为堆芯上、下部功率。

本文以ACP-100模块式小型反应堆为例进行算法研究，采用SCIENCE程序包中的堆芯扩散计算程序SMART进行功率能力分析，生成7 740套不同工况下的功率分布。

4 数值结果

使用LS-SVM算法和ACE算法时，均采用1 105套功率分布及模拟探测器信号作为训练集，进行回归分析，剩下的6 635套则作为验证集。将两种算法重构的功率分布与SMART程序计算得到的功率分布进行对比。对LS-SVM算法和ACE算法的重构效果定义4个评价量：

Avg.RMS=

(15)

Max.RMS=

(16)

(17)

(18)

表1列出LS-SVM算法与ACE算法在功率分布整体重构精度上的对比，其中T代表训练集，V代表验证集。

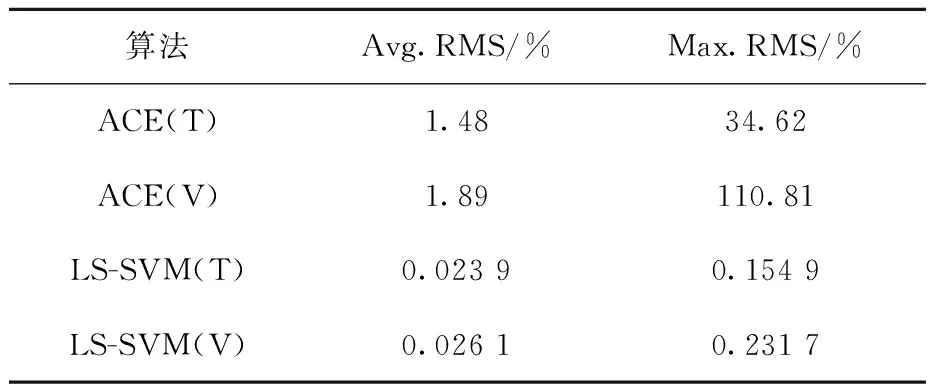
表1 LS-SVM算法与ACE算法的功率分布重构精度对比Table 1 Comparison of power distribution reconstruction accuracy between LS-SVM and ACE

为了给出具体节块的重构精度对比，使用式(17)、(18)分别计算节块功率重构的均方根误差及最大误差。图1示出LS-SVM算法的均方根误差和最大误差，图2示出ACE算法的均方根误差和最大误差。

由图1、2和表1可看出：1) LS-SVM算法的均方根误差与最大误差均在可接受范围内，重构精度明显优于ACE算法，LS-SVM重构得到的功率分布更接近SMART计算得到的功率分布；2) ACE算法的均方根误差在合理可接受范围内，但其重构中可能出现的最大误差过大。

图1 LS-SVM算法的节块功率重构均方根误差和最大误差Fig.1 Node power reconstruction RMS error and maximum error of LS-SVM

图2 ACE算法的节块功率重构均方根误差和最大误差Fig.2 Node power reconstruction RMS error and maximum error of ACE

在实际的探测器测量时，其测量值总是带有一定程度的噪声，假设探测器的读数测量值Dmeasure与理论值Dtheoretic之间有关系如下：

(19)

其中：ε为随机数，ε服从均值为0、标准差为1的正态分布；δ为噪声水平，在进行功率重构算法研究时，通常设定为1%。

为衡量LS-SVM算法的抗噪声能力，对每个节块定义节块功率重构效果的评价量如下：

(20)

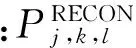
图3示出不同噪声水平时LS-SVM算法的功率分布重构效果。由图3可知：1) 基于LS-SVM的功率重构方法的均方根误差与探测器测量噪声水平近似有一正比例关系；2) 在典型堆内探测器噪声水平下，基于LS-SVM的功率重构算法的重构精度符合要求，具有良好的抗探测器噪声干扰能力。

5 结论

准确的轴向功率分布对于反应堆的安全性有着极其重要的作用，本文实现了LS-SVM在堆芯轴向功率分布中的应用，利用ACP-100模块式小堆第1循环不同工况下的7 740套功率分布进行了算法的验证，并得到如下结论：1) LS-SVM算法的重构精度远优于ACE算法，在不考虑探测器噪声的情况下，ACE算法的功率分布最大重构误差可达到110%，而LS-SVM算法的功率分布最大重构误差仅为0.23%左右；2) 在考虑噪声的情况下，LS-SVM算法具有良好的抗噪声干扰能力，重构误差与探测器噪声水平呈正比关系。

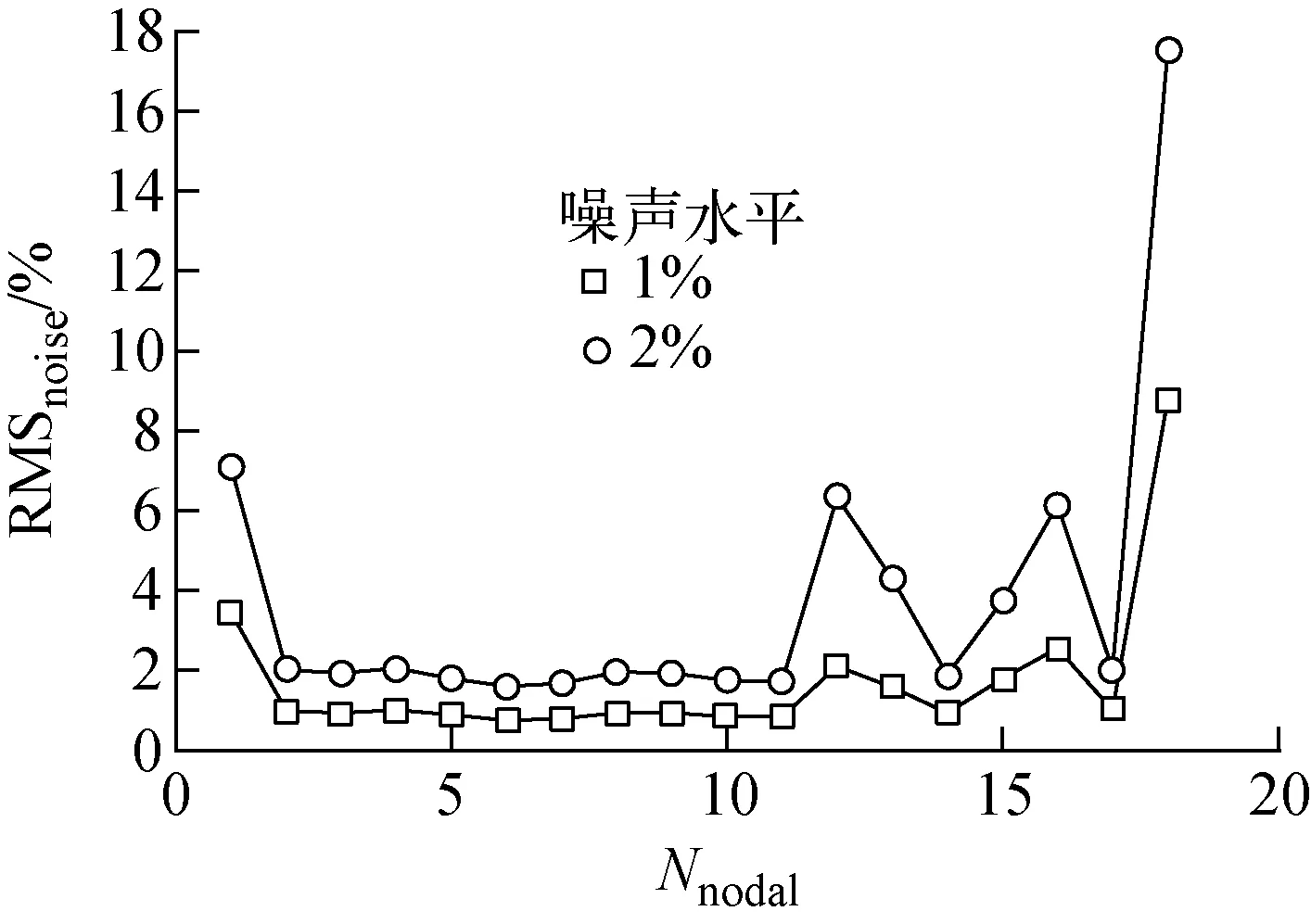
图3 LS-SVM算法带噪声的节块功率重构均方根误差Fig.3 Node power reconstruction RMS error of LS-SVM with noise

本文仅考虑了ACP-100模块式小堆单一循环下的轴向功率分布重构，下一步工作主要集中在以下两点：1) 使用ACP-100模块式小堆其他循环下更多工况的功率分布进行LS-SVM算法的验证，以保证LS-SVM算法在整个反应堆的运行历史中均能进行精确的功率分布重构；2) 在实际的反应堆在线监测应用中，能够直接获取三维堆内探测器测量数据。将本文提出的算法与径向功率分布重构算法(如耦合系数法)相结合，可进行全堆三维功率分布的重构计算。

[1] LEE E K, KIM Y H, CHA K H, et al. Reconstruction of core axial power shapes using the alternating conditional expectation algorithm[J]. Annals of Nuclear Energy, 1999, 26(11): 983-1 002.

[2] BAE I H, NA M G, LEE Y J, et al. Calculation of the power peaking factor in a nuclear reactor using support vector regression models[J]. Annals of Nuclear Energy, 2008, 35(12): 2 200-2 205.

[3] 王晓龙，盖秀清，蔡琦，等. 基于重构概念的变负荷工况下核功率预测研究[J]. 原子能科学技术，2012，46(增刊)：351-355.

WANG Xiaolong, GAI Xiuqing, CAI Qi, et al. Study of reactor power prediction during load change process based on signal reconstruction[J]. Atomic Energy Science and Technology, 2012, 46(Suppl.): 351-355(in Chinese).

[4] 孙斌，周云龙，赵鹏，等. 基于奇异值分解和最小二乘支持向量机的气-液两相流流型识别方法[J]. 核动力工程，2007，28(6):62-66.

SUN Bin, ZHOU Yunlong, ZHAO Peng, et al. Identification method for gas-liquid two-phase flow regime based on singular value decomposition and least square support vector machine[J]. Nuclear Power Engineering, 2007, 28(6): 62-66(in Chinese).

[5] JIANG Botao, ZHAO Fuyu. Particle swarm optimization-based least squares support vector regression for critical heat flux prediction[J]. Annals of Nuclear Energy, 2013, 53(1): 69-81.

[6] VAPNIK V. Statistical learning theory[M]. New York: Springer Verlag, 1998.

Application of Least Square Support Vector Machine in Core Power Distribution Reconstruction

PENG Xing-jie1,2, LI Tian-ya2, LI Qing2, WANG Kan1

(1.DepartmentofEngineeringPhysics,TsinghuaUniversity,Beijing100084,China; 2.ScienceandTechnologyonReactorSystemDesignTechnologyLaboratory,NuclearPowerInstituteofChina,Chengdu610041,China)

The application of the least square support vector machine (LS-SVM) to core axial power distribution reconstruction was researched, and 18-node powers were reconstructed from six-level in-core detector signals. Axial power distributions of 7 740 cases of ACP-100 modular reactor were used to verify the accuracy of the LS-SVM reconstruction method. The results show that the LS-SVM method performs much better than the alternating conditional expectation (ACE) method and the LS-SVM method has good robustness.

least square support vector machine; power distribution reconstruction; robustness

2014-01-22;

2014-10-08

彭星杰(1991—)，男，湖南怀化人，博士研究生，核科学与技术专业

TL362

A

1000-6931(2015)06-1026-06

10.7538/yzk.2015.49.06.1026