摇摆状态下矩形通道内弹状流压力模型
阎昌琪,金光远,孙立成,闫超星
(哈尔滨工程大学 核安全与仿真技术国防重点学科实验室,黑龙江 哈尔滨 150001)
摇摆状态下矩形通道内弹状流压力模型
阎昌琪,金光远,孙立成,闫超星
(哈尔滨工程大学 核安全与仿真技术国防重点学科实验室,黑龙江 哈尔滨 150001)
本文通过可视化方法对竖直与倾斜条件下矩形通道内弹状流单元的参数进行研究,尝试给出摇摆状态下矩形通道内弹状流压力模型。通过图像处理给出气弹段空泡份额以及两相速度的计算关系式,并验证漂移流模型在液弹段的适用性,给出弹状流单元的长度份额以及空泡份额的计算关系式。根据实验结果给出摇摆条件下矩形通道内弹状流压力组分的模型,并重点分析摩擦压降模型的适用程度。结果表明,弹状流压力模型可很好地预测摇摆条件下矩形通道内的压力。
摇摆运动;矩形通道;弹状流;压力模型
弹状流可认为是间歇流、脉动流或不稳定流,由于这种流动不可避免地存在于化工、航空、电子、核动力设备等行业中,国内外学者对弹状流特性开展了大量研究[1-6],弹状流的气液压力波动形式多样,不同的通道截面,气液占有的份额、速度以及加速度皆不同。目前,对于弹状流的研究仍停留在物理模型的建立或物理模型中部分参量的研究方面。
对于充分发展的弹状流,每个弹单元一般分成两部分:第一部分是气弹单元,主要由气弹头部、气弹体、气弹尾部以及周围的液膜组成;第二部分是液弹单元,由气弹尾部引起的高度搅混的气液混合体和气泡分散分布的连续液相组成。对于弹状流模型的建立,除了对于流场、压力场和气弹尾部的尾流夹带的专项研究外,一般都会忽略气弹末尾的气液混合体,这部分一般占有液弹长度很小的份额,对于整体的阻力特性或压力预测影响不大。
摇摆运动是一种典型的海洋条件,国内关于摇摆条件下热工流体的研究主要集中在哈尔滨工程大学等单位。曹夏昕等[7]通过建立竖直圆管内弹状流单元的质量守恒方程和弹状流稳定存在条件等方程,对摇摆条件下竖直圆管内充分发展的弹状流单元的物理模型进行计算,主要给出了关于空泡份额的计算。本工作针对摇摆条件下矩形通道内弹状流单元的参数特征,使用高速摄影仪对局部特征参数进行拍摄,根据实验结果给出摇摆条件下对弹状流摩擦阻力的预测。
1 实验装置与实验内容
测量系统、气回路以及水回路三大部分组成实验系统。实验工质为空气和去离子水。空气由压气机压缩后储存在储气罐中。空气从储气罐流出后,通过减压阀保证压力稳定,经过气相质量流量计(质量流量计,型号Promass83,量程0~10 L/min,精度0.1)测量流量后,进入混合腔,流经实验段后,最终在实验段上方排入大气。水箱内的水在水泵驱动下,分别流经流量调节阀和流量计(质量流量计,型号Promass83,量程0~6 500 kg/h,精度0.1),流入混合腔后,与来自气回路的空气充分混合,之后进入实验段,最终回到水箱。
实验系统图如图1所示,本实验选取的矩形通道为长2 000 mm、宽40 mm、高3 mm的透明有机玻璃矩形通道,其通道宽高比为13.3,水力直径为5.58 mm。长、宽、高的测量误差分别为±0.1 mm、±0.02 mm和±0.02 mm。两个压力传感器安装在试验段宽边方向,距离为1 000 mm,为消除入口段效应,下测压点布置在距入口500 mm处(L/D=89.6),压力传感器选用精度等级为0.1的PR35X压力变送器,上、下测压点压力变送器量程分别为100 kPa和250 kPa。
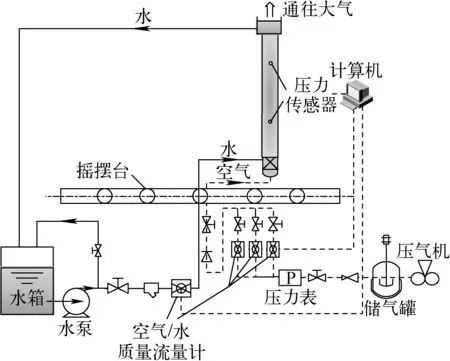
图1 实验系统示意图Fig.1 Schematic diagram of experimental system

图2 摇摆台侧视图Fig.2 Side view of rolling platform
流量与压力信号由NI数据采集系统采集,采样频率定为256 Hz。实验中的实验段主体管路固定在摇摆台架上,通过胶质软管与供水供气系统连接,摇摆台如图2所示。摇摆台由液压驱动,根据设定的摇摆周期和角度绕转轴做正弦摇摆运动,可设定的摇摆周期和角度范围分别为5~16 s和5°~30°,摇摆台自带角度的采集系统,与实验段流量及压力信号采集保持同步。实验中选取的摇摆工况为:θm=5°/T=8 s、θm=10°/T=8 s、θm=15°/T=8 s、θm=15°/T=12 s、θm=15°/T=16 s,其中θm为摇摆幅度,T为摇摆周期,摇摆台逆时针转动为摇摆运动的正角度。
摇摆台运动规律如下:
1) 角度
(1)
2) 角速度
(2)
3) 角加速度
(3)
实验中使用到的可视化测量系统示意图如图3所示,可通过图像的记录测量空泡份额、气弹速度等参数,实验中主要观测竖直与倾斜条件下气弹段和液弹段空泡份额以及气液速度的特征。

图3 可视化测量系统示意图Fig.3 Schematic diagram of flow optical measurement system
2 可视化测量结果
2.1 气弹段气液流速及空泡份额
本实验中通过图像处理得到竖直条件下气弹的速度vg-TB,基于漂移流给出的气弹段的方程式为:
(4)
其中:jg为气相折算速度;j为两相折算速度;αTB为气弹段空泡份额;vgj-TB为相应的漂移速度;C0为矩形通道的分布系数。
图4示出气弹段通过图像处理得到的气弹速度与两相折算速度的变化规律。文献[8]提到的有关结论,在气液层流区域,当倾斜的角度增加时,分布系数变小,漂移速度增加;对于气液湍流区域,当倾斜角度增加时,分布系数与漂移速度保持不变。本实验中同样对于倾斜状态弹状流区域的气弹速度进行了研究,通过图4中给出的拟合关系式对气液层流状态下气弹速度进行计算,对倾斜角度分别为10°、20°和30°的情况,其平均相对误差分别为9.8%、12.3%和14.7%,因此,竖直条件下得到的气弹区域漂移流公式可使用在倾斜状态下的气液层流区域中。根据气弹段空泡份额可计算气弹段的气弹速度和液膜速度vl-TB。
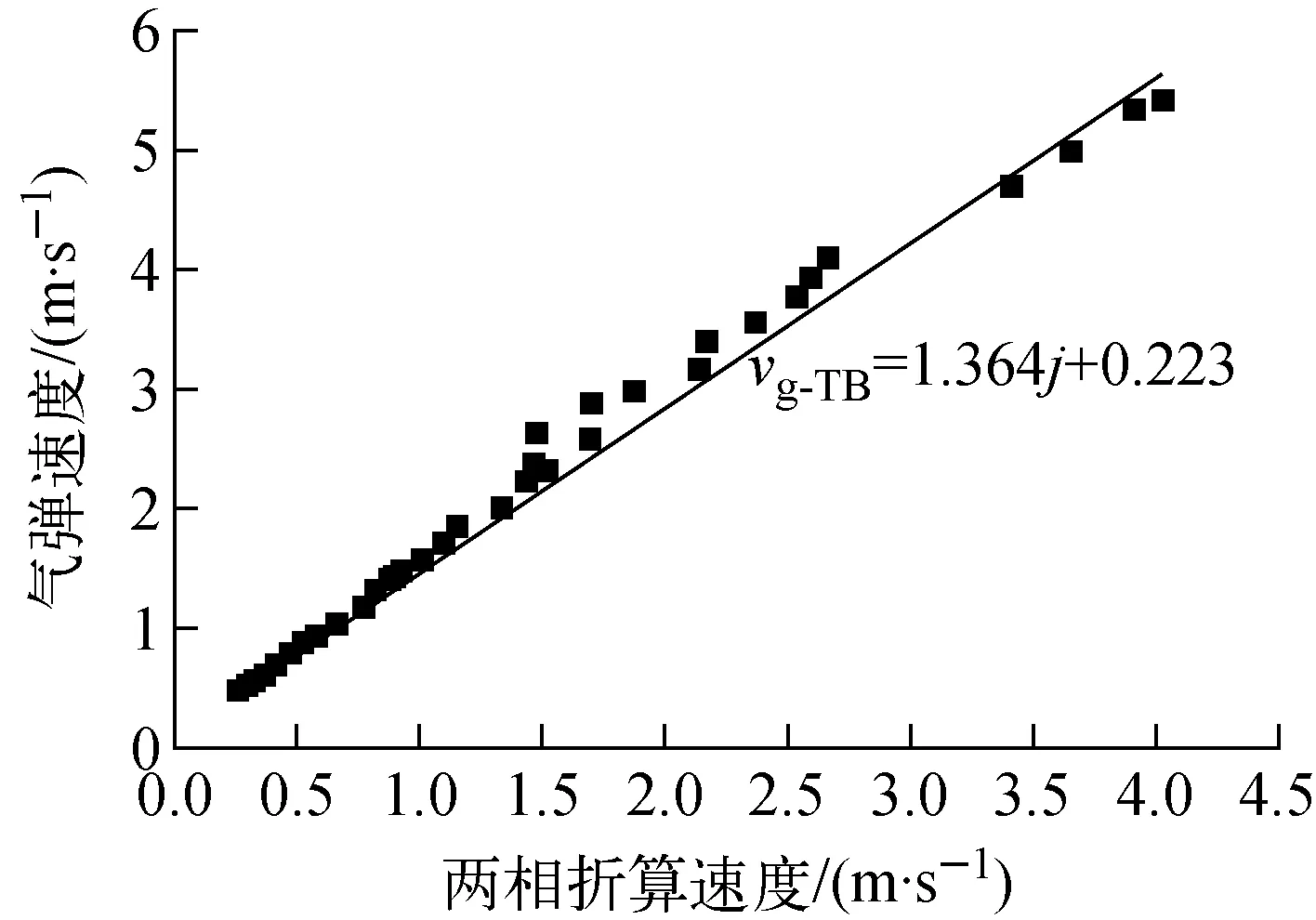
图4 竖直条件下不同两相折算速度下气弹速度的变化Fig.4 Variation of Taylor bubble velocity with two-phase superficial velocity under vertical condition
2.2 液弹段气液流速及空泡份额
本实验中通过图像处理得到竖直条件下液弹的速度,基于漂移流给出的液弹段的速度表达式为:
(5)
其中,C0取1.337。
液弹中的漂移速度根据文献[9]进行计算,其形式为:
(6)
其中:D为通道当量直径;σ为表面张力;Δρ为两相密度差;ρl为液相密度;DB为特征气泡直径,通过式(7)进行计算:
(7)
倾斜条件下只需将重力加速度g转换成对应倾斜条件下的重力加速度分量。
由此得到的液弹段的平均空泡份额与实验值相比,其平均相对误差在±14.2%范围内,因此可通过式(5)计算竖直和倾斜条件下液弹单元的空泡份额。
2.3 弹状流单元参数
对于由一个气弹单元和其下部的液弹单元构成的一个弹状流单元的整体研究,从模型定义的参数讲,主要是确定气弹长度份额ε和整体空泡份额α。
弹状流中,气弹段占有的长度份额的定义是弹状流中每个弹状流单元中气弹长度占总弹状流单元长度的比值,其表达形式如下:
(8)
其中:LTB为气弹段长度,m;LLS为液弹段长度,m;LSF为弹单元长度,m。
文献[10]认为气弹单元的长度主要与管内气液折算速度有关,给出的气弹段单元的长度计算关系式为:
(9)
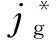
(10)
(11)
对于液弹单元的长度,选取文献[11]提出的竖直条件下弹状流中平均液弹长度进行计算:
(12)
其中,ReLS为气弹特征液相雷诺数,通过以下方法计算:
(13)
根据式(9)、(12)和(13)可计算竖直和倾斜条件下矩形通道内的平均气弹长度份额。
在弹状流单元中,另一个重要的物理量就是总空泡份额α,其计算形式如下:
(14)
3 摇摆状态下矩形通道内弹状流压力模型
3.1 摇摆条件下矩形通道内空泡份额的预测
图5为摇摆台运动到角度θ处,弹单元(包含一个完整气弹段和液弹段的单元)的物理模型,重要的长度或速度参数在图上都有体现。由图5可看出,若要求出摇摆条件下弹单元的空泡份额,需要知道相关的气弹速度、气弹段空泡份额、气弹段液膜速度、液弹段空泡份额、液弹段气泡平均流速、液弹段液相流速、液弹段空泡份额以及泰勒泡长度和液弹长度确定的气弹长度份额等参数。
在以上提出的弹状流单元模型中,可认为任意截面的两相折算速度均相等。
(15)

图5 摇摆条件下弹状流单元的模型示意图Fig.5 Diagram of slug flow unit model in rolling motion
对于泰勒泡段的空泡份额,由于倾斜条件对于竖直条件下得到的气弹段漂移流模型的影响可忽略,本研究中忽略摇摆条件对于泰勒泡段漂移速度的影响,仅保留摇摆条件对其分布系数的影响。
vg-TB=1.364Kj+0.223
(16)
其中,K为摇摆条件引起的影响因子,由参考文献[12]确定。
对于液弹段的空泡份额的计算,应考虑到摇摆条件对于漂移速度和截面分布系数的影响,因此,摇摆条件下液弹段的漂移流模型的表达式为:
(17)
其中,aeff为沿通道方向上的重力加速度与摇摆条件下的有效加速度分量,计算方法参考文献[7]。
3.2 摇摆条件下矩形通道内摩擦阻力的预测
对于泰勒泡段,其摩擦阻力主要由气相和液相受到壁面的摩擦阻力加和得到,图6示出摇摆条件下泰勒泡段截面的模型示意图。

图6 摇摆条件下泰勒泡段截面的模型示意图Fig.6 Diagram of cross-section of Taylor bubble in rolling motion
泰勒泡段的摩擦压降梯度(ΔpTB)f/LTB主要分为气弹受到的摩擦力梯度与液膜受到的摩擦力梯度,其表达形式为:
(18)
气弹受到的摩擦力梯度可表示为:
(19)
其中,h1和h2分别为气弹两边缘与通道边缘的距离。
单相气体在摇摆条件下受到的壁面切向应力τg-TB可表示为:
近年来,北京市委、政府乃至中央对通州的发展战略和职能做出一系列的指示,提出“聚焦通州战略,打造功能完备的城市副中心”的目标,要求其要积极融入首都发展大局,要担起承接与疏解首都城市的双重责任,要构建清新明亮、多组团集约紧凑发展的生态城市布局,要着力打造国际一流、和谐宜居之都示范区、新型城镇化示范区、京津冀区域协同发展示范区. 通州以大运河为骨架,沿六环路为创新发展轴,依托水网、绿网和路网构建12个民生共享组团,形成了“一带一轴多组团”的空间格局,并将水城共融、蓝绿交织、文化传承作为城市特色,努力塑造活力之城、生态之城、智慧之城、人文之城、幸福之城的美好形象.
(20)
其中:ρg为气相速度;摇摆条件下矩形通道内单相摩擦阻力系数λg-roll的计算参考文献[13]。
液膜中由于带有极少量气体,大部分都是分散小气泡,虽然液膜厚度有限,但是稳态的图像结果表明,液膜中空泡份额最高只有0.08,与单相水的阻力特性相差无几,因此对液膜的计算可认为是对单相水的计算。液膜受到的摩擦力梯度可表示为:
(21)
其中,s为通道间隙。
单相液体在摇摆条件下受到的壁面切向应力τl-TB可表示为:
(22)
关于图6中摇摆条件下的h1和h2两个长度的计算,由于在空泡份额的预测中可得到泰勒泡段的空泡份额,其与h1和h2两个长度满足如下关系:
(23)
其中,ATB、A分别为气弹截面积和通道截面积。
由此可得:
(24)
对于液弹段受到的摩擦压力梯度(ΔpLS)f/LTB,由于可认为液弹段为气泡均匀分布的泡状流,其摩擦压力梯度的计算形式为:
(25)
泡状流在摇摆条件下受到的壁面切向应力τLS可表示为:
(26)
其中,摇摆条件下矩形通道内泡状流摩擦阻力系数λLS-roll的计算参考文献[14]。
最终得到的摇摆条件下矩形通道内的平均摩擦压降梯度(Δp)f/LSF的表达形式为:
(27)
弹状流单元的重位压降梯度(Δp)g/LSF计算形式为:
(28)
将弹状流中的附加压降认为是摇摆条件作用于整体两相流整体的压力,弹状流单元的附加压降梯度(Δp)add/LSF形式为:
(29)
其中:z1和z2分别为上下测压点与摇摆台的距离;y1为摇摆转轴与实验段的距离。
局部压力损失梯度(Δp)loss/LSF的形式为:
(30)
其中,局部压力损失系数ζ与液相在气弹段与液弹段的空泡份额的比值有关:
(31)
本研究将摩擦压降从总压降中分离出来,重点研究摩擦压降的预测值与实验值的符合程度。
3.3 摇摆条件下矩形通道内弹状流摩擦压降预测公式的评价
图7示出了预测结果与实验值的整周期平均值与瞬态相对摩擦压降的比较。由图7可看出,对于摩擦压降的预测,超过95%的点落入±30%范围内。预测值能基本预测摇摆条件下矩形通道内弹状流摩擦压降的瞬态波动特性,但在所有的结果中,预测值的波动幅度均小于实验值。分析原因是因为重位压降、附加压降和局部压力损失的预测均为在弹状流单元长度上的平均值。

图7 摇摆条件下不同矩形通道内弹状流摩擦压降梯度平均值Fig.7 Averaged value of frictional pressure drop gradient in different rectangular channels under rolling condition
本研究提出摇摆条件下矩形通道内摩擦压降的目的在于尝试正向预测实验结果,并非对于实验结果数据进行拟合求出经验关系式,但对于摩擦压降幅度的预测还不够精确,需要对其进一步细化,找到更适合于矩形通道中弹状流摩擦压降的预测经验公式。
4 结论
1) 通过图像处理方法得到了竖直条件下矩形通道内气弹区域漂移流公式,并在倾斜条件下进行验证,发现其可使用于倾斜状态。
2) 给出了液弹段和弹状流单元的空泡份额计算关系式,并对实验结果进行了验证。
3) 根据实验结果给出了摇摆条件下压力各组分的计算关系式,在总压降中分离出摩擦压降的实验值并与预测值进行比较,结果表明摇摆条件下矩形通道内弹状流模型可很好地预测实验结果。
[1] CAREW P S, THOMAS N H, JOHNSON A B. A physically based correlation for the effects of power law rheology and inclination on slug bubble rise velocity[J]. Int J Multiphase Flow, 1995, 21: 1 091-1 106.
[2] BONNECAZE R H, ERISKINE W, Jr, GRESKOVICH E J. Holdup and pressure drop for two-phase slug flow in inclined pipelines[J]. AIChE J, 1971, 17: 1 109-1 113.
[3] van HOUT R, BARNEA D, SHEMER L. Translational velocities of elongated bubbles in continuous slug flow[J]. Int J Multiphase Flow, 2002, 28: 1 333-1 350.
[4] ZHENG D H, CHE D F. Experimental study on hydrodynamic characteristics of upward gas-liquid slug flow[J]. Int J Multiphase Flow, 2006, 32: 1 191-1 218.
[5] 王洋,阎昌琪,孙立成,等. 竖直窄矩形通道内弹状流中液膜特性研究[J]. 原子能科学技术,2014,48(1):33-38.
WANG Yang, YAN Changqi, SUN Licheng, et al. Study on liquid film characteristics of slug flow in vertical narrow rectangular channel[J]. Atomic Energy Science and Technology, 2014, 48(1): 33-38(in Chinese).
[6] 闫超星,阎昌琪,孙立成,等. 竖直小通道内弹状流气弹长度的计算模型[J]. 原子能科学技术,2014,48(7):1 182-1 187.
YAN Chaoxing, YAN Changqi, SUN Licheng, et al. Calculation model of slug length for slug flow in vertical small channel[J]. Atomic Energy Science and Technology, 2014, 48(7): 1 182-1 187(in Chinese).
[7] 曹夏昕,阎昌琪,孙中宁. 摇摆状态下竖直管内弹状流单元物理模型解析[J]. 核动力工程,2007,28(3):47-50.
CAO Xiaxin, YAN Changqi, SUN Zhongning. Analysis of slug flow unit model in rolling vertical tube[J]. Nuclear Power Engineering, 2007, 28(3): 47-50(in Chinese).
[8] YAN C X, YAN C Q, SUN L C, et al. Slug behavior and pressure drop of adiabatic slug flow in a narrow rectangular duct under inclined conditions[J]. Annals of Nuclear Energy, 2014, 64: 21-31.
[9] ABDUL-MAJEED G H. A comprehensive mechanistic model for vertical and inclined two-phase flow[D]. Baghdad: University of Baghdad, 1997.
[10]WANG X, GUO L, ZHANG X. An experimental study of the statistical parameters of gas-liquid two-phase slug flow in horizontal pipeline[J]. Int J Heat Mass Transfer, 2007, 50(11-12): 2 439-2 443.
[11]ZHANG H, ZHU S. A hydrodynamic model of gas-liquid upward slug flow in vertical tubes[C]∥3rd Int Conl on Multiphase Flow. Xi’an: [s. n.], 1994: 1 063-1 070.
[12]JIN G, YAN C, SUN L, et al. Void fraction of dispersed bubbly flow in a narrow rectangular channel under rolling conditions[J]. Progress in Nuclear Energy, 2014, 70: 256-265.
[13]幸奠川. 摇摆对矩形通道内流动阻力特性的影响研究[D]. 哈尔滨:哈尔滨工程大学,2013.
[14]金光远,阎昌琪,孙立成,等. 周期惯性力影响下矩形通道泡状流阻力特性[J]. 化工学报,2013,64(4):1 198-1 203.
JIN Guangyuan, YAN Changqi, SUN Licheng, et al. Frictional characteristics of bubbly flow in rectangular channel under periodic force[J]. Journal of Chemical Industry and Engineering, 2013, 64(4): 1 198-1 203(in Chinese).
Pressure Model of Slug Flow in Rectangular Channel in Rolling Motion
YAN Chang-qi, JIN Guang-yuan, SUN Li-cheng, YAN Chao-xing
(FundamentalScienceonNuclearSafetyandSimulationTechnologyLaboratory,HarbinEngineeringUniversity,Harbin150001,China)
The visualization method was used to investigate the parameters of slug flow unit in rectangular channel (40 mm×3 mm) under vertical and inclined conditions, aiming at establishing the pressure model of slug flow in rectangular channel in rolling motion. The calculation correlations for void fraction and two-phase velocity for gas slug segment were acquired, and the applicability of drift flux model was confirmed for liquid slug segment. The length fraction and void fraction of slug flow unit were calculated. According to the experiment results, the pressure model of slug flow model was established, and the predicted frictional pressure drop turned out to be in a good agreement with the experiment value.
rolling motion; rectangular channel; slug flow; pressure model
2014-01-21;
2014-07-23
国家自然科学基金资助项目(11175050,51376052)
阎昌琪(1955—),男,黑龙江哈尔滨人,教授,硕士,从事核动力装置性能、反应堆热工水力及气液两相流研究
TL334
A
1000-6931(2015)06-1062-07
10.7538/yzk.2015.49.06.1062

