一维Fokker-Planck方程的有限体积法求解及其在中性束注入加热中的应用

张 能，龚学余,，黄千红，侯 伟，谢宝艺，余江妹，李景春

(1.南华大学 数理学院，湖南 衡阳 421001;2.南华大学 核科学技术学院，湖南 衡阳 421001)



一维Fokker-Planck方程的有限体积法求解及其在中性束注入加热中的应用

张 能1，龚学余1,2，黄千红2,*，侯 伟2，谢宝艺1，余江妹1，李景春2

(1.南华大学 数理学院，湖南 衡阳 421001;2.南华大学 核科学技术学院，湖南 衡阳 421001)

采用有限体积法数值求解一维Fokker-Planck方程，通过模拟电子自碰撞过程进行程序校验。研究表明，有限体积法能高效求解Fokker-Planck方程，能确保分布函数的非负性和粒子数密度守恒，同时计算程序能有效克服传统求解方法中出现的分布函数对麦克斯韦分布的过冲现象。模拟了HL-2A装置在中性束注入加热等离子体过程中，离子分布函数和温度随时间的演化情况。结果表明，随着中性束的注入，离子分布函数出现非麦克斯韦化，离子温度迅速增加后稳定；计算结果和实验结果符合较好。进一步讨论束能量和功率的影响，随束能量和功率的增加，等离子体离子温度均升高，离子温度随束能量的增加升高的幅值较大，而随束功率的增加升高的幅值较小。

有限体积法；Fokker-Planck方程；分布函数演化；中性束注入加热

中性束注入(neutral beam injection，NBI)加热的物理机制较明晰且具备加热效率高等特点，已成为高温等离子体辅助加热最有效的方法之一，目前在国内外的主要托卡马克装置中已得到广泛应用[1-4]。在HL-2A托卡马克装置中，已进行了不同参数下的中性束注入加热实验，并取得很好的加热效果。2009年，在中性束注入和电子回旋共振加热(ECRH)条件下实现了国内的首次H模放电[5]；此后，借助中性束注入加热系统，开展了一系列重要的等离子体物理实验研究，包括等离子体输运和约束改善研究[6]、L-H转换机理研究[7]、高能量粒子物理学和磁流体不稳定性研究[8]等；2013年，在1.5 MW中性束注入加热实验中，单独用0.6 MW的束功率同样获得了H模放电[9]。因此，对HL-2A装置进行中性束注入加热实验的同时，有必要展开相关的数值模拟研究，为以后的实验提供参考。

为更深入了解中性束注入后等离子体温度的演化及其影响因素，需求解相应的Fokker-Planck方程。Fokker-Planck方程传统的求解是采用有限差分法进行，计算结果对网格点步长和时间步长均有很严格的要求以确保分布函数的非负性和粒子数守恒[10-13]；文献[14]利用有限元法数值求解一维Fokker-Planck方程，模拟了高斯分布的电子经过自碰撞趋于麦克斯韦分布的过程，但已开发的程序与传统上用差分方法的求解程序一样，对麦克斯韦分布存在过冲现象[15]。

本文推导一维Fokker-Planck方程有限体积法计算格式，数值模拟电子自碰撞由超高斯分布趋于麦克斯韦分布的过程，并进行程序校验。进一步模拟HL-2A装置中性束注入加热过程中，离子分布函数和温度随时间的演化情况，并讨论束功率和能量的影响。

1 一维Fokker-Planck方程的有限体积法求解

等离子体中的带电粒子与德拜球内其他粒子相互作用中，会发生多重小角度碰撞，使带电粒子速度不断出现微小的随机性变化，能准确描述这种粒子系统的动力学方程是Fokker-Planck方程：

(1)

(2)

(3)

(4)

式中：i、j为网格点；n为粒子种类数；Z为携带的电荷数；lnΛ为库仑对数；Hn和Gn为Rosen-bluth势函数。

假设等离子体各物理量在空间均匀分布且不受外力作用的影响，采用的粒子分布函数只与速度的大小和时间有关。Fokker-Planck方程可简化成：

(5)

其中：

(6)

式中：a、b为粒子种类；上标a/b为粒子a碰撞b；nb为粒子b的密度；q为电荷数。则Rosenbluth势函数表示为：

(7)

(8)

对式(5)使用有限体积法处理，方程两边同时积分：

(9)

对速度项积分，得到：

(10)

其中：ΔV为控制容积体积；A为控制容积边界面积。采用Chang的方法[11]近似表示fi-1/2和fi+1/2：

(11)

(12)

(13)

为验证计算格式的正确性，模拟速度空间一维情况下电子自碰撞由超高斯分布趋于麦克斯韦分布的过程，首先令电子速度分布函数为超高斯分布：

(14)

图1a示出了用有限体积法计算的电子分布函数随时间的演化，图中标记为M的曲线为麦克斯韦分布函数。由图可知，开始阶段分布函数趋于麦克斯韦平衡分布的速度较快，经很短时间后分布函数趋于麦克斯韦平衡分布的速度越来越慢，经过100个时间步，分布函数和麦克斯韦分布函数基本重合，经过1 000个时间步，分布函数几乎无变化，说明此时基本达到平衡态。图1b为有限元方法计算的结果[14]，由图可知，低能区域的分布函数较麦克斯韦分布偏高，高能区域的分布函数偏低。这表明本文程序有效克服了计算过程中对麦克斯韦分布存在的过冲现象。图2为电子数密度随时间的演化关系，表明有限体积法能保证电子数守恒。

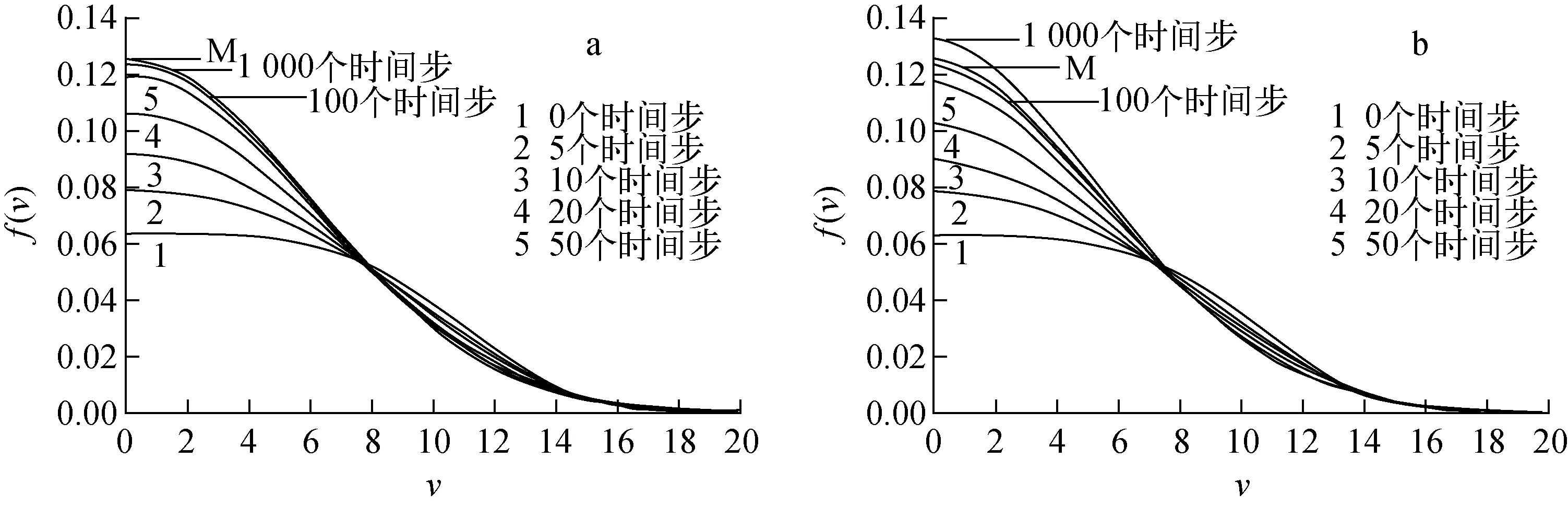
a——有限体积法；b——有限元方法

图2 电子数密度的演化曲线Fig.2 Evolution curve of electron number density

通过有限体积法求解一维Fokker-Planck方程，数值模拟了一维情况下电子自碰撞由超高斯分布趋于麦克斯韦分布的过程，证明了计算格式和程序能确保电子分布函数的非负性和电子数密度守恒，表明了有限体积法对于求解Fokker-Planck的高效性。

2 HL-2A装置上中性束注入加热模拟

在上述高效求解Fokker-Planck方程的基础上，进一步模拟在中性束注入加热条件下的一维Fokker-Planck方程：

(15)

其中，S为中性束注入的源项，用高斯函数来模拟其束流：

(16)

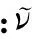
计算采用HL-2A托卡马克装置中性束注入加热实验参数：大半径R=1.65 m，小半径r=0.4 m；等离子体电流Ip=480 kA，磁场强度Bt=2.8 T，等离子体中离子密度n0=1.5×1019m-3；在中性束注入前由欧姆加热到的离子温度(以能量表示)为Ti=400 eV；中性束注入功率为600 kW，能量为40 keV，计算得到的流强J=2.965×1018m-3·s-1。

由于离子与离子碰撞交换能量的时间较离子与电子碰撞短很多，因而中性束注入产生快离子的能量主要交给本底离子。所以在计算中，始终将电子的分布当作麦克斯韦分布来处理。计算离子的温度随中性束注入的变化：

(17)

图3 离子分布函数的演化曲线Fig.3 Evolution curve of ion distribution function

图3示出了中性束注入加热过程中离子分布函数的演化曲线。结果表明，随着中性束的注入，低能量的离子数减少，高能量的离子数增加，离子分布函数出现非麦克斯韦化。

图4示出了中性束注入加热过程中离子温度的演化情况。由图可知，中性束注入加热等离子体初始阶段离子温度迅速上升，产生的快离子迅速将能量传递给本底离子；碰撞耗散和离子吸收能量平衡后，离子能量不再上升，在加热的后阶段，由于高能粒子能量的损失，离子温度出现缓慢下降，这与实验中中性束注入加热等离子体时的离子温度演化曲线相符[17]。

图4 离子温度的演化曲线Fig.4 Evolution curve of ion temperature

图5为在其他参数不变的情况下，束功率分别取600、700、800 kW得到的温度演化曲线。结果表明，提高中性束的注入功率，可提升离子温度的爬升速度，使等离子体更快达更高温度，但温度幅值变化不大。图6为在其他参数不变的情况下，束能量分别取40、50、60 keV得到的温度演化曲线。结果表明，提高中性束的能量，能快速提升中性束的加热温度，且温度幅值有较大的提升。

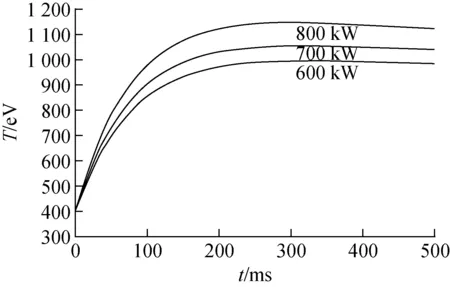
图5 不同束功率下离子温度的演化曲线Fig.5 Evolution curve of ion temperature for different beam powers

图6 不同束能量下离子温度的演化曲线Fig.6 Evolution curve of ion temperature for different beam energy

3 结论

本文通过有限体积法数值求解一维Fokker-Planck方程，数值模拟一维速度空间超高斯分布电子经自碰撞趋于麦克斯韦分布的过程，证明有限体积法能高效求解Fokker-Planck方程。进一步模拟了HL-2A装置中性束注入加热的情况，得到了离子分布函数随中性束注入出现非麦克斯韦化。计算了离子温度的演化曲线，与实验结果符合较好。讨论了中性束的功率和能量的影响，结果表明，随着束功率和能量的升高，离子温度升高，相较而言，随束能量的增大离子温度升高的幅值较大。由于数值模拟中性束注入加热过程中采用了一维速度空间近似，所以现有计算程序及模拟结果存在不足。在中性束注入加热过程中，需考虑中性束注入角度对加热效率、功率沉积等的影响，以便研究更多的物理问题，这也是下一步工作要考虑的问题。

[1] HU L Q, KURIYAMA M, AKINO N, et al. Beam divergence and power loading on the beamline components of the negative-ion based NBI system for JT-60U[J]. Fusion Engineering and Design, 2001, 54(2): 321-330.

[2] AKERS R J, APPEL L C, CAROLAN P G, et al. Neutral beam heating in the START spherical Tokamak[J]. Nucl Fusion, 2002, 42(2): 122-135.

[3] CIRIC D, BROWN D P D, CHALLIS C D, et al. Overview of the JET neutral beam enhancement project[J]. Fusion Engineering and Design, 2007, 82(5-14): 610-618.

[4] ZOHM H, ADAMEK J, ANGIONI C, et al. Overview of ASDEX upgrade results[J]. Nucl Fusion, 2009, 49(10): 104009.

[5] DUAN X R, DONG J Q, YAN L W, et al. Preliminary results of ELMy H-mode experiments on the HL-2A Tokamak[J]. Nucl Fusion, 2010, 50(9): 095011.

[6] XIAO W W, ZOU L N, DING X T, et al. Observation of a spontaneous particle-transport barrier in the HL-2A Tokamak[J]. Phys Rev Lett, 2010, 104: 215001.

[7] CHENG J, DONG J Q, ITOH K, et al. Dynamics of low-intermediate-high confinement transition in toroidal plasma[J]. Phys Rev Lett, 2013, 110: 265002.

[8] DUAN X R, DING X T, DONG J Q, et al. An overview of recent HL-2A experiments[J]. Nucl Fusion, 2013, 53(10): 104009.

[9] 严龙文，段旭如，丁玄同，等. HL-2A装置物理实验研究的进展[C]∥第十六届全国等离子体科学技术会议. 上海：复旦大学，2013.

[10]MIRIN A A, McCOY M G, TOMACCHKE G P, et al. FPPAC88: A two-dimension multispecies nonlinear Fokker-Planck package[J]. Comput Phys Comm, 1988, 51(3): 373-380.

[11]SHOUCRI M, SHKAROFSKY I. A fast 2D Fokker-Planck solver with synergetic effects[J]. Comput Phys Commun, 1994, 82(2-3): 287-305.

[12]PEYSSON Y, SHOUCRI M. An approximate factorization procedure for solving nine-point elliptic difference equations: Application for a fast 2-D relativistic Fokker-Planck solver[J]. Comput Phys Commun, 1998, 109(1): 55-80.

[13]KARNEY C F F. Fokker-Planck and quasilinear codes[J]. Comput Phys Rep, 1986, 4(3-4): 183-244.

[14]翁苏明，盛正明. 等离子体中Fokker-Planck方程的有限元模拟[J]. 计算物理，2007，24(2)：134-140.

WENG Suming, SHENG Zhengming. Finite element scheme for Fokker-Planck equation in plasmas[J]. Chinese Journal of Computational Physics, 2007, 24(2): 134-140(in Chinese).

[15]SHKRAROFSKY I P, JOHNSTON T W, BACKYNSKI M P. The particle kinetics of plasmas[M]. Netherlands: Addison-Wesley Publishing Company, 1966: 132-137.

[16]王建国，李有宜，李建刚. HT-6M中性束注入加热理论分析[J]. 物理学报，1995，44(1)：92-97.

WANG Jianguo, LI Youyi, LI Jiangang. Theoretical study for neutron beam injection heating[J]. Acta Physica Sinica, 1995, 44(1): 92-97(in Chinese).

[17]PAN C H. Overview of the auxiliary heating systems for HL-2A Tokamak[M]∥Southwestern Institute of Physics Annual Report 2007. Chengdu: Southwestern Institute of Physics, 2007.

One-dimensional Fokker-Planck Equation Solving by Finite Volume Method and Its Application in Neutral Beam Injection Heating

ZHANG Neng1, GONG Xue-yu1,2, HUANG Qian-hong2,*, HOU Wei2,XIE Bao-yi1, YU Jiang-mei1, LI Jing-chun2

(1.SchoolofMathematicsandPhysics,UniversityofSouthChina,Hengyang421001,China; 2.SchoolofNuclearScienceandTechnology,UniversityofSouthChina,Hengyang421001,China)

The one-dimensional Fokker-Planck equation was solved by finite volume method. The reliability of program was verified by simulation of electron self-collision. The results show that the numerical scheme assures positive distribution function and particle number conservation. It is an effective method of solution for Fokker-Planck equation. And the overshoot of the Maxwell distribution that arouse from Fokker-Planck equation solving by traditional numerical method was eliminated. Furthermore, the evolutions of ion distribution function and temperature were simulated in neutral beam injection heating on the HL-2A. The results show that the ion distribution function tends to non-Maxwell distribution as the neutral beam injects, and the ion temperature rises rapidly and then reaches stability. The effects of beam power and energy on the ion temperature were investigated, and the results show that the ion temperature increases with the beam power and energy. The change is more obvious by increasing beam energy than power.

finite volume method; Fokker-Planck equation; evolution of distribution function; neutral beam injection heating

2014-12-02;

2015-01-26

国际热核聚变实验堆计划专项资助项目(2014GB108002)；国家自然科学基金资助项目(11375085)；湖南省核聚变与等离子体物理创新团队建设资助项目(NHXTD03)；衡阳市科技局资助项目(2013KJ24)；南华大学研究生科研创新资助项目(2014XCX08,2014XCX02)

张 能(1989—)，男，湖南桃江人，硕士研究生，从事核聚变与等离子体物理研究

*通信作者：黄千红，E-mail: hqhhgy@163.com

O532.26

A

1000-6931(2015)06-0966-06

10.7538/yzk.2015.49.06.0966