Mallat小波滤波器系数的计算与地质应用

赵应权， 沈忠民， 周爱芬

(1. 成都理工大学 a.“油气藏地质及开发工程”国家重点实验室，b.能源学院，成都 610059;2．中国石油工程建设公司，北京 100120)



Mallat小波滤波器系数的计算与地质应用

赵应权1a，b， 沈忠民1a， 周爱芬2

(1. 成都理工大学 a.“油气藏地质及开发工程”国家重点实验室，b.能源学院，成都 610059;2．中国石油工程建设公司，北京 100120)

针对第一类、第二类Mallat系列小波的滤波器公式为频率域的表达式，它们无法直接求得对应系列小波的滤波器系数，从而造成了Mallat系列小波在时间域内多尺度计算的困难。这里基于傅里叶分析原理，借用MATLAB工作平台编制了由频率域到时间域的Mallat系列小波滤波器组的求解代码。该段代码解决了Mallat系列小波在时间域内的滤波器系数求解。经实际数字计算表明，采用该方法求得的滤波器组系数进行多尺度分析，能够实现小波的完全分解与重构，这对选用Mallat系列小波中的具体小波进行异常检测分析，具有十分重要的意义。

Mallat小波； 异常检测； FFT； 滤波器系数

0 引言

小波在奇异性信号的检测上具有独特的优势，在图像边缘检测、网络异常检测、地震异常与语音异常识别等领域有着广泛地应用[1-5]。然而用不同的小波处理相同的信号数据序列有着不同的处理结果，为了取得更好的处理结果， Mallat[6]针对图像边缘提取发明了一类B样条小波，即Mallat小波。前人利用Mallat小波做过重力异常多尺度反演研究[7]，也用该小波提取过深层次物化探的异常信息[8]，Zhang et.al[9-11]应用该小波在油气化探异常信号的分离中也取得了良好效果。

Mallat小波分奇数阶B样条小波和偶数阶B样条小波两类。Mallat仅给出了任意阶第一类小波，即小波函数关于原点反对称的小波函数ψ、尺度函数φ、滤波器组H、G、K、L的频率响应表式。刘曙光[12]补充了任意阶第二类B样条小波，即小波函数关于原点对称的小波的推导公式，并给出了该类小波滤波器组H、G、K、L的解析表达式。

由于Mallat小波的滤波器系数在实际应用中受待处理数据影响，需要选用Mallat系列小波中不同阶次的小波。因此，不同阶次的Mallat小波的滤波器系数在实际计算中显得尤为重要。但是在前人研究中，仅有Mallat小波滤波器系数的频率域解析公式，工程技术人员很难利用这些公式直接求得不同阶次小波的滤波器系数，这势必影响到Mallat小波的多尺度计算，从而大大降低了Mallat小波的实用价值。为此作者用Matlab语言求解了Mallat小波的滤波器系数。

1 滤波器系数公式

滤波器是实现小波多尺度分析计算的重要参数。Mallat小波以样条函数为平滑函数θ，以样条函数的一阶导函数ψ′(x)或二阶导函数ψ″(x)为小波函数。Mallat小波的平滑函数阶数的奇偶性与小波函数的对称性不同，滤波器系数的求解公式也有所不同。具体的求解公式为式(1)与式(2)。

(1)

(2)

在式(1)中，只要平滑函数θ的阶数相同，对应的第一类小波与第二类小波在小波的分解与重构中有着相同的低通滤波器系数。在式(2)中，平滑函数θ的阶数并不对高通滤波器产生作用，仅受小波类型的影响，对于第一类小波，G(ω)为奇函数，具有关于原点反对称的特点，对于第二类小波，G(ω)为偶函数，具有关于原点对称的特点。这两类小波的对称性的不同，正好对应于图像边缘检测的极值检测与零点检测两种检测方式。

由于Mallat小波分析中的另外两个滤波器K、L与H、G有着定量的解析关系，它们之间的相关关系为：

(3)

(4)

式(3)、式(4)中的H(ω)、G(ω)对应于式(1)、式(2)中的H(ω)、G(ω)，将参数H(ω)、G(ω)代入式(3)、式(4)后经傅立叶逆变换可以解出时间域内的K、L滤波器系数。

2 滤波器系数求解

根据前文的滤波器函数在频率域的解析表达式，采用快速傅里叶变换(FFT)及逆变换(IFFT)的方法求取Mallat小波的滤波器系数。具体求解的步骤(图1)：

1)针对单个频谱周期，根据Nyquist采样定理初步确定采样点数N1。

2)针对傅里叶分析要求，修正采样点数为N2，且N1≤N2,N2=2N,N∈Z+。

3)根据修正的采样点数N2，求得采样的平均间隔dw。

4)对一个完整的频率周期2π按照dw的采样间隔平均采样，并计算出各个相位上对应的离散信号序列x[i]。

5)对步骤4)中的离散信号序列x[i]进行傅里叶逆变换和中心移位，得到时间域内的信号序列y[i] 。

6)取步骤5)中的离散信号序列y[i]的模得到实信号序列z[i]，截除实信号序列z[i]两侧的“0”值，剩余的数据即为Mallat小波在时间域内的滤波器系数。

根据上述操作步骤，采用matlab语言实现了这一求解过程。以平滑函数θ阶数为奇数的第一类Mallat小波为例，设定平滑函数的阶数m=3时，滤波器H、G、K、L的matlab数字求解代码如表1所示。

其他滤波器系数可参考公式(1)-公式(4)用类似的方法求解，运行上述代码本文求得平滑函数是3阶、4阶Mallat小波的滤波器系数如表2所示。

3 应用实例

3.1 地表油气化探干扰识别

东营凹陷金东-柳桥地区地表油气化探数据中干扰严重，为从这些数据中提取有效的异常信息，需要排除干扰。前人基于异常与干扰的频率差异，发明了小波排除干扰的方法[9-11]。针对金东-柳桥地区的地表油气化探数据，作者采用平滑函数阶次为3的Mallat反对称小波，进行了干扰排除与异常信息的识别。图2为该区酸解烃甲烷在东西测线上的干扰与异常分析图，其中低频序列对应着干扰信息，高频序列对应着异常信息，由图2可以看出，无论是干扰，还是异常在空间位置上都一一对应，并且具有继承性，这为后续的干扰排除，准确地提取异常信息提供了可能。

图1 Mallat小波滤波器系数数字求解过程图

表1 第一类Mallat小波的滤波器系数求解代码

3.2 层序地层划分

元坝地区是中国石化继普光气田后在川东北地区台地边缘超深层领域内，又一个取得重大突破的区块。前人的大量研究认为，川东北地区长兴组储层分布明显受Ⅲ级层序体系域及沉积相控制，储层主要分布于SQ1、SQ2及SQ3的高位体系域中[13]。因而层序的快速准确划分，为长兴组—飞仙关组储层的时空展布提供预测依据，也可促进该区天然气勘探的快速发展。

地层纵向的周期性为使用小波划分层序提供了理论依据，前人在实践中发现不同小波在层序划分中存在较大差异[14]，即小波分析手段划分出的层序界面位置围绕实际层序界面位置的上下波动，因此采用小波方法划分层序往往需要大量的人工调整。考查这些用于划分层序的小波发现，前人使用的小波大都为Daubechies小波、Symlets小波和DMeyer小波，这些小波在对称性或紧支性上较差，容易造成分析数据序列中的异常值的“漂移”，进而导致层序界面点不准。而Mallat小波作为边缘检测的最佳小波，正好客服了上述不足。以元坝地区的122井二叠统的长兴组地层为例，结合地层标志人工划分该段地层为2个三级层序，7个四级层序，16个五级层序(图3)。采用小波划分该段地层时发现，DB4小波划分出的层序界面位置较人工解释界面位置有较大偏差，相邻的四级、三级层序在层序界面点上也并不具有很好的继承性；而用平滑函数阶次为3的Mallat反对称处理的结果跟人工解释的层序界面完全一致，这样就大大减少了人工调整层序界面位置的工作量。

表2 平滑函数阶数为3、4的Mallat小波滤波器系数

注：m.平滑函数的阶数，T.小波类型，H.低通滤波器，G.高通滤波器，K.重构高通滤波器，L.二维小波重构滤波器

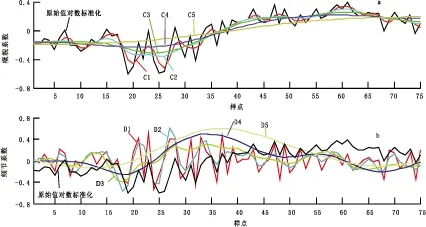
图2 金东-柳桥地区酸解烃甲烷东西测线上的Mallat小波分析图

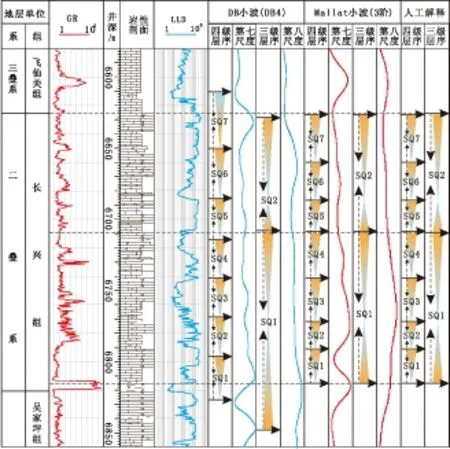
图3 川东北元坝122井地层层序划分图

4 结论

基于傅里叶分析原理，利用Matlab平台求解了Mallat系列小波在时间域内的滤波器系数。傅里叶分析是联接时间域与空间域计算的纽带，Matlab软件的数据可视化、数据分析以及数值计算简洁便利、人机交互能力强的特点，为Mallat小波系数的求解提供了条件。在Nyquist采样定理的约束下，对周期范围内的数据实行采样离散化，然后利用傅里叶分析手段，在Matlab工作平台编制的由频率域到时间域的Mallat系列小波滤波器组的求解代码，这组代码解决了mallat系列小波在时间域内的滤波器系数求解。

[1] 韩慧妍，韩燮．基于方向小波变换的边缘检测算法[J]. 微电子学与计算机，2012, 29(7): 55-57. HAN H Y, HAN X. Edge detection algorithm based on directional wavelet transform[J]. Microelectronics & computer. 2012, 29(7): 55-57.(In Chinese)

[2]冯兴杰，焦文欢. 基于动态阈值的网络异常检测[J]. 计算机工程与设计，2012, 33(6): 2182-2186. FENG X J, JIAO W H. Network abnormality detection based on dynamic threshold[J]. Computer engineering and design, 2012, 33(6): 2182-2186.(In Chinese)

[3]解滔，杜学彬，刘君，等．汶川Ms8.0、海地Mw7.0地震电磁信号小波能谱分析[J]．地震学报，2013, 35(1):61-71. XIE T, DU X B, LIU J, et al. Wavelet power spectrum analysis of the electromagnetic signals of Wenchuan Ms8.0 and Haiti Mw7.0 earthquakes[J]. Acta seismologicaca sinica. 2013, 35(1):61-71.(In Chinese)

[4]李卫，宋弘，姜天华．基于小波神经网络的嵌入式语音识别系统[J]. 通信技术, 2010, 43(6): 213-218. LI W, SONG H, JIANG T H. Embedded speech recognition system based on wavelet neural network[J]. Communications Technology. 2010, 43(6): 213-218.(In Chinese)

[5]敬少群，刘春平, 王佳卫．小波变换在深井水位异常识别中的应用[J]. 地震研究, 2012, 35(2): 171-176. JING S Q，LIU CH P，WANG J W. Application of wavelet multi-scaling decomposition in identifying water level anomaly of deep well[J]. Journal of seismological research. 2012, 35(2): 171-176.(In Chinese)

[6]STEPHANE MALLAT, SIFEN ZHONG. Characterization of signals from multiscale edges[J]. IEEE Transactions on pattern analysis and machine intelligence, 1992, 14(7): 710-732.

[7]LIUPING ZHANG, GUOPING BAI,KEBIN ZHAO. Restudy of acid-extractable hydrocarbon data from surface geochemical survey in the Yimeng Uplift of the Ordos Basin, China: Improvement of geochemical prospecting for hydrocarbons[J]. Marine and Petroleum Geology, 2006(23): 529-542.

[8]LIUPING ZHANG, GUOPING BAI. A wavelet-analysis-based new approach for interference elimination in geochemical hydrocarbon exploration[J]. Mathematical Geology, 2003, 35(8): 939-952.

[9]ZHANG LIUPING, RUAN TIANJIAN. Application of wavelet analysis to interference elimination for geochemical hydrocarbon exploration[J]. Journal of China University of Geosciences, 2000, 11(1): 89-91.

[10]侯遵泽，杨文采．重力异常多尺度反演研究及应用[C]．中国地球物理学会年会，2011. HOU Z, YANG W C. Study on multi-scale inversion of gravity anomalies[C]. The Chinese Geographics annual meeting, 2011.(In Chinese)

[11]陈建国，夏庆霖．利用小波分析提取深层次物化探异常信息[J]．地球科学-中国地质大学学报，1999， 24(5)：509-512. CHEN J G, XIA Q L. Wavelet-based extraction of geophysical and geochemincal anomaly information[J]. Earth Science—Journal of China University of Geosciences, 1999, 24(5): 509-512.(In Chinese)

[12]刘曙光．基于边缘检测算子的两类B样条小波[J]．纺织高校基础科学学报，2001，14(1)：66-71. LIU SH G. Two types of the B-spline wavelets based on edge detector[J]. Basic sciences journal of textile universities. 2001, 14(1): 66-71.(In Chinese)

[13]郭彤楼．川东北元坝地区长兴组—飞仙关组台地边缘层序地层及其对储层的控制[J]．石油学报，2011，32(3)：387-394. GUO T L. Sequence strata of the platform edge in the Changxing and Feixianguan formations in the Yuanba area,northeastern Sichuan basin and their control on reservoirs[J]. Acta petrolei sinica, 2011, 32(3): 387-394.(In Chinese)

[14]朱剑兵，纪友亮，赵培坤，等．小波变换在层序地层单元自动划分中的应用[J]．石油勘探与开发，2005，32(1)：84-86. ZHU J B, JI Y L, ZHAO P K, et al. Application of wavelet transform in auto-identify units of stratigraphy sequence[J]. Petroleum Exploration and Development, 2005, 32(1):84-86.(In Chinese)

Geological application and calculation of Mallat wavelet filter coefficients

ZHAO Ying-quan1a,b, SHEN Zhong-min1a, ZHOU Ai-fen2

(1.Chengdu University of Technology a. State Key Laboratory of Oil & Gas Reservoir Geology and Exploration, b. college of Sedimentary，Chengdu 610059, China；2.China Petroleum Engineering & Construction Corp., Beijing 100120,China)

Formulae for the 1st and 2nd type of Mallat series wavelet filters are expressed in frequency domain, the wavelet filter coefficients cannot obtained by the corresponding formula directly. Thus, it is difficult to calculate in multi-scale analyzing for the Mallat series wavelet in time domain. In this paper, based on the principle of Fourier analysis, some solving code is complied for the Mallat series wavelet filter's from the frequency domain to the time domain by the MATLAB language. This code solves the filter coefficients for Mallat series of wavelet in time domain. The actual number calculation shows that decomposition and reconstruction of wavelet calculate in multi-scales can be achieved completely by the filter coefficients from the method above-mentioned, and it has great significance for anomaly detection to select a specific Mallat wavelet.

Mallat wavelet; anomaly detection; FFT; filter coefficient

2013-12-23 改回日期：2014-09-15

国家科技重大专项项目(2008ZX05008-004-20);“油气藏地质及开发工程”国家重点实验室开放基金项目( PLC201102)

赵应权(1977-)，男，博士，主要从事油气勘探研究工作，E-mail: hbszzyq@126.com。

1001-1749(2015)04-0532-06

P 628

A

10.3969/j.issn.1001-1749.2015.04.19