2.5维复电阻率反演并行算法设计

陈 实， 吴文鹂， 顾观文， 梁 萌

(中国地质科学院 地球物理地球化学勘查研究所，廊坊 065000)



2.5维复电阻率反演并行算法设计

陈 实， 吴文鹂， 顾观文， 梁 萌

(中国地质科学院 地球物理地球化学勘查研究所，廊坊 065000)

近年来2.5维复电阻率反演取得了一些理论和应用方面的成果，但计算过程复杂、计算量巨大，特别是正演计算过程中计算量大导致了反演速度较慢。这里在2.5维复电阻率反演计算基础上，将反演算法中的正演过程的排列和频率循环分割成多个规模较小的程序段，并发执行正演过程中的每个排列和频率循环的求解计算过程，并根据并行计算的节点数目或者计算核心数目，动态调整每个节点或者计算核心的计算量，从而提高了算法的计算效率和适应性。

复电阻率; 并行计算; 2.5维反演

0 前言

在2.5 维复电阻率反演过程中，正演模拟计算过程比较复杂、数据处理与计算量大限制了该反演算法的实用性，因此在原有计算精度的基础上提高计算速度，已经成为该领域研究的重点。提高程序运算速度主要采取两种方法：①从算法入手改进算法的设计,提高算法的计算效率(如采用更有效求解复线性方程组算法等)；②从计算设备入手，采用多核或者计算机集群并行计算来实现为程序加速。这里采用多核计算机，在保持2.5 维复电阻率反演算法主体结构的基础上，将反演过程中的正演过程按照排列和频率循环分割形成新的计算线程，并将新的计算线程分解到不同的计算核心上，以实现程序的并行计算，减少了算法的运行时间，提高了算法的运算速度，程序结构相对简单，可以在较少修改的情况下部署到其他计算平台上。

1 2.5维复电阻率反演原理与并行计算分析

赵广茂[1]对2.5 维复电阻率反演理论过程做了初步推导。范翠松[2]对该反演过程进行了进一步说明。

为提高反演稳定性，对参数进行归一化处理即令

x=(ln(ρ0))，ln(m)，ln(τ),ln(c))，并以此构建单一排列的反演目标函数：

φ=‖Uaa-UaA(x)‖+ ‖Uφφ-Uφφ(x)‖+μλ‖R‖

(1)

式中：a和φ分别为观测电场的振幅向量与相位向量；A(x)和φ(x)分别为电场振幅与相位的正演函数；Ua和Uφ为归一化对角阵；λ是阻尼因子；μ为缩放系数；R为模型的二阶光滑度算子矩阵。 将式(1)在xk邻域线性展开并极小化得到实系数反演方程组：

(2)

其中：ΔdA和Δdφ分别为电场振幅和相位的绝对拟合差向量；LA和Lφ分别为电场振幅与相位的灵敏度矩阵；Δxk为模型修正向量,通过求解方程(2)即可得到xk+1，进入下次迭代过程。当利用N个排列进行反演时，由于公式(2)为线性过程，通过求解左端灵敏度相关项，并作线性累加求和，并将右端项线性累加求和整理得到新方程组(3)。

(P+μλRTR)·Δxk=B

(3)

其中：P为灵敏度矩阵求和；B为右端项拟合差向量求和。通过式(3)得到线性方程组并求解该线性方程组即可实现多个排列的繁衍计算。根据上述理论分析可以得到2.5维复电阻率，其反演计算流程如图1所示。

1)读取程序使用的数据和模型参数。

2)计算反演光滑度算子矩阵。

3)调用正演计算模块进行正演计算并生成形成反演矩阵。

4)调用反演模块求解反演线性方程组[5]，并更新模型参数。

5)调用正演计算模块进行计算误差。

6)判断误差是否收敛。误差不收敛则返回步骤4)，误差收敛继续判断误差是否小于停止运算指定误差，误差大于停止运算指定误差则返回步骤3)进行下一次迭代。误差小于或等于停止运算指定误差则停止运算输出反演结果。

实验中运用的算例观测方式为偶极-偶极，模型共进行了6个排列的数据采集，每个排列10个观测点，发射偶极长度为100 m，接收偶极长度为100 m。数据采集的工作频率分别为0.02 Hz、0.1 Hz、1 Hz、8 Hz、32 Hz、128 Hz。模型计算采用有限元法，地电模型剖分网格见图2，水平方向剖分为55块，深度方向地面以上剖分为10层，地面以下剖分为18层。

根据上述剖分过程和计算流程，对原有串行算法各个中间过程进行时间统计，其中读取数据和模型参数用时为0.52 s，计算反演光滑度矩阵用时为42.2 s。迭代一次计算过程中，正演计算模型变化量并形成反演矩阵的过程计算时间为7 537.13 s，求解反演矩阵并更新模型过程为57.32 s，正演误差计算过程共用时间1 758.96 s。

表1 计算模块时间统计表

根据上述时间统计图正演计算过程占整个迭代过程计算时间的79%，反演过程中正演计算合成过程占整个迭代计算时间的18.4%，反演求解线性方程组过程只占迭代计算时间的1%左右。如果能将正演计算和反演中正演合成过程实现并行计算就可以大幅度提高整个迭代计算过程的运算速度。

2 正演过程并行算法实现

2.1 并行算法计算量分配方案

正演过程每个排列和频率的计算过程相对独立并且结构相似，适合进行并行计算，在并行计算结束时，将每一个计算单元计算出的地表场合成反演线性方程组的左端项和右端项。反演算法正演过程并行分解粒度可以用排列级、频率级[6]、波数级和观测点级。根据算法实际实现过程中所选择的实验平台，最终确定并行分解粒度为规模适中的频率级，即正演计算过程中有m个排列、每个排列有n个频率，每个频率存在t个计算波数，实验平台存在u个计算核心，将程序分解为m*n个计算线程，其中每个计算核心分配m*n/u个计算线程[7]，其流程描述见图2。

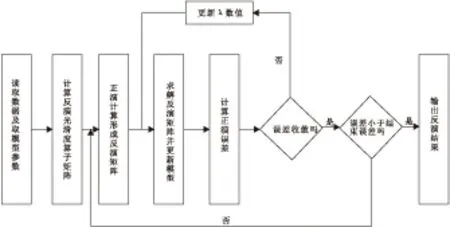
图1 2.5 维复电阻率反演计算流程图

图2 并行计算过程分解

2.2 并行过程程序设计

由于整体程序采用Fortran实现，所以上述算法中涉及的并行过程可以采用支持Fortran的并行开发包MPI或者OpenMP实现[8]。其中MPI适合用于多进程并行计算[9]，主要用于将计算程序分解到网络中的多个计算节点上，实现并行计算或者将程序分解成多个计算进程，每个计算进程虽然工作在同一个计算机上，但是每个计算进程有独立的数据与存储空间，计算进程相互独立，无法实现数据直接访问，计算进程间数据传输依靠MPI_Send和MPI_Recieve函数通过网络数据传输实现[10]。OpenMP主要用于实现单进程多线程并行运算，其并行过程采用线程实现，多个并行过程数据共享采用栏栅或者临界区实现，比较适合程序结构较复杂，中间共享数据结构较多的程序实现并行计算[11]。针对2.5 维复电阻率反演算法程序，采用OpenMP实现并行计算。

3 反演并行算法算例分析

实验所选工作计算机为DELL双核12线程核工作站，工作频率为3.46 GHz，内存为24 G。算例模型为6个排列，每个排列10个观测点，6个工作频率，地电模型水平方向剖分为55块，深度方向剖分为28层。异常体位置见图3，其中异常体的中心为(600,-200),长度和宽度分别为200 m。

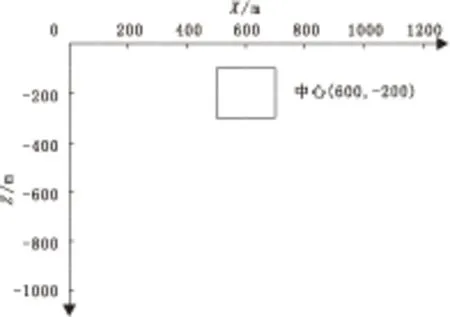
图3 异常体位置

反演每次迭代运行时间对比见表2。

并行反演迭代20次运行结果如图4，其中异常体中心在(600,-200),结果与算例模型相符，与串行程序结果相同。

保持该算例10个观测点、6个工作频率，分别取1个排列、2个排列、3个排列、4个排列、5个排列和6个排列重新构造算例，进行串行和并行运算时间对比，对比结果见图5。

由图5可以看出，串行计算过程计算时间随计算量增加而线性增加，并行计算过程每个排列被按照频率数分解为6个计算线程，计算核心有12个。排列数为1时计算线程共6个，分配在6个计算核心上，其余6个计算核心闲置，并行运算时间为串行运算时间的20.7 %；排列数为2时，计算线程为12个，分配在12个计算线程上，12个计算核心全部参加运算，运算时间比1个排列稍有增加，并行运算时间为串行运算时间的11.3 %；排列数大于等于3时，前12个计算线程分别在12个计算核心上进行计算，待某个计算核心计算完成后，在剩余计算线程选择一个调度到空闲的计算核心进行计算，其中排列数为3时，并行运算时间为串行运算时间的13.0 %，排列数为4时，并行运算时间为串行运算时间的10.2 %，排列数为5时，并行运算时间为串行运算时间的12.4 %，排列数为6时，并行运算时间为串行运算时间的10.8 %。

由此可以看出，并行计算时间也随计算量缓慢增加，其斜率与总计算线程数和计算核心数目的比值成正比，假设为每个计算核心的计算时间Ti，并行计算时间曲线的斜率和Ti的最大值MAX(Ti)成正比。

表2 每次迭代并行和串行时间对比

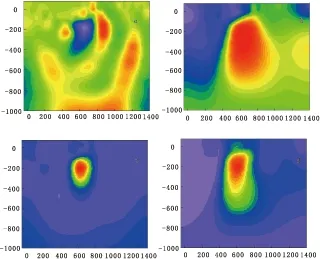
图4 反演断面图

图5 不同排列串行与并行时间对比

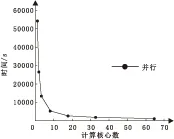
图6 并行计算时间和计算核心数关系图

保持该算例6个排列、10个观测点、6个工作频率，将程序移植HP9000 Superdome服务器上，该机型体系结构为IA-64,CPU工作频率为1 598 MHz，计算核心分别取1～64个，其运行时间见图6。

并行计算时间随着计算核心数增加而迅速下降，由于算例中计算量被分为36组共36个计算线程，当计算核心增加到36以上时，前36个计算核心参与计算，后面的计算核心并未参与工作，计算时间与36个计算核心时基本相同。

算例实验使用了两种运行环境，其中Dell T7500工作站(2核6线程)具有12个计算核心全部参与运算，CPU工作频率为3 460 MHz，HP9000 Superdome(64核)具有64个运算核心，CPU工作频率为1 598 MHz，其中参与运算的工作核心数为36，其运行时间对比见表3。其中Dell T7500工作站为当前最新的计算工作站，其指令结构和编译器优化程度较高，所以其整体加速效果优于HP9000 Superdome服务器。

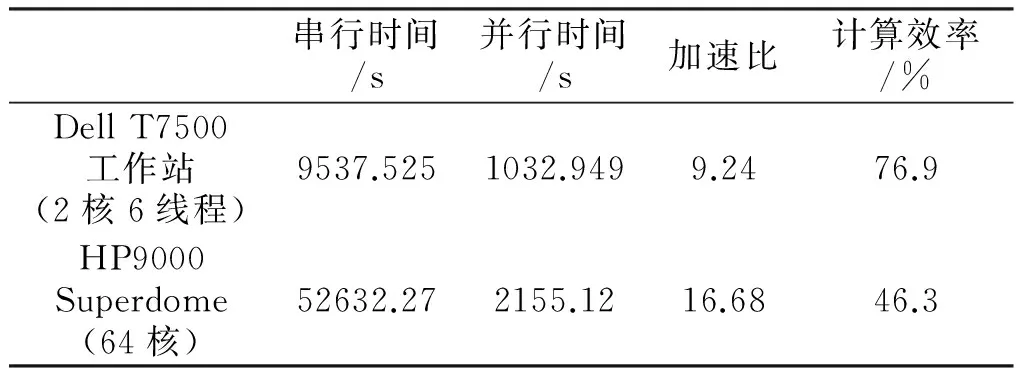
表3 不同平台运行时间对比

4 结论

1)反演并行计算程序在保持原有精度的基础上，使原有串行程序能够在多核计算机上进行并行运算，充分利用计算平台的计算资源，提高了程序的运算速度。

2)在划分并行任务的颗粒度时，在充分使用计算核心的前提下，每次分配给计算核心的任务量尽量大。因为在并行任务开始时需要对每个计算核心分配资源，每次分配资源耗时相对较多，例如开辟多维数组，如果计算任务相对较小，则本次分配资源占用的比例相对较高，程序的运行效率就会比较低。

[1] 赵广茂.带地形的复电阻率2.5维电磁场正反演研究[D].长春：吉林大学,2009. ZHAO G M. Research of complex resistivity 2.5D electromagnetic forword and inversion with topography[D]. Changchun:Jilin University,2009.(In Chinese)

[2] 范翠松,李桐林,严加永.2.5维复电阻率反演及其应用试验[J].地球物理学报,2012,55(12):4045-4046. FAN C S,LI T L,YAN J Y. Research and application experiment on 2.5D SIP inversion[J].Chinese Journal of Geophysics,2012,55(12):4045-4046.(In Chinese)

[3] 王家映.地球物理反演理论[M].北京:高等教育出版社,2002. WANG J Y. Inversion theory of physical geography[M].Beijing:Higher education press,2002.(In Chinese)

[4] 李金铭.地电场与电法勘探[M].北京:地质出版社,2005. LI J M. Geoelectricity and electrical prospecting[M].Beijing: Geological Press,2005.(In Chinese)

[5] 安学庆.求解大型稀疏线性方程组算法研究[D].郑州:郑州大学,2006. AN X Q. The solution of large-scale sparse linear system of equations algorithm research[D]. Zhengzhou: Zhengzhou University,2006.(In Chinese)

[6] 李焱,胡祥云,吴桂桔,等.基于MPI的二维大地电磁正演的并行计算[J].地震地质,2010,32(3): 392-401. LI Y,HU X Y, WU G J, et al. Parallel computation of 2-D magnetotelluric forward modeling based on MPI[J].Seismology and Geology,2010,32(3):392-401.(In Chinese)

[7] 顾观文, 梁萌, 吴文鹂.基于并行处理的CSAMT拟二维反演解释[J].物探与化探.2010，34(3):400-402. GU G W,LIANG M ,WU W L.The quasi two dimensional inversion and interpretation of CSAMT based on parallel processing.Geophysical and Geochemical Exploration,2010,34(3):400-402.(In Chinese)

[8] Barry Wilkinson Michael Allen.并行程序设计 [M] . 陆鑫达,译.北京:机械工业出版社, 2005. BARRY WILKINSON MICHAEL ALLEN. Design of parallel programing[M].Lu Xinda, Beijing: Mechanical Industry Press, 2005.(In Chinese)

[9] 蒋英,雷永梅.基于MPI的几种算法的并行编程通用算法[J].计算机工程与应用.2003,(03):140-141. JIANG Y,LEI Y M. Parallel programming universal algorithm of several algorithms based on MPI[J]. Computer Engineering and Applications.2003,(03):140-141.(In Chinese)

[10]曾志峰.Linux环境下MPI并行编程与算法实现研究[J].航空计算技术.2004,32(2):62-64. ZENG ZH F. Under the environment of Linux MPI parallel programming and algorithm implementation research[J].Aeronautical Computer Technique.2004,32(2):62-64.(In Chinese)

[11]潘小敏,皮维超,盛新庆.基于共享内存的高效OpenMP并行多层快速多极子算法[J].北京理工大学学报.2012.2(32):165-166. PAN X M,PI W CH,SHENG X Q. Efficient parellelization of multilevel fast multipole algrithm based on OpenMP[J].Transactions of Beijing Institute of Technology.2012.2(32):165-166.(In Chinese)

Design of 2.5 dimensional complex resistivity inversion parallel computing scheme

CHEN Shi,WU Wen-li,GU Guan-wen,LIANG Meng

(Institute of Geophysical and Geochemical Exploration, CAGS, Langfang 065000, China)

Some theoretical and application aspects of results have been made for 2.5 dimensional complex resistivity inversion, but complex mathematical calcultionsin forward processes slow down the inversion speed. Based on the 2.5 dimensional complex resistivity inversion，the forward processes of the inversion algorithm will be divided into much smaller forward cycles accordingtoits arrangement and frequency.the amount of calculations will be assigned dynamically to each node or the calculation core depending on the number of nodes or the calculation of the number of parallel computing core, therefore the adaptability and efficiency of the algorithm will be greatly improved in this way.

complex; resistivity; parallel algorithmparallel algorithm; 2.5 dimensional inversion

2014-12-29 改回日期：2015-04-24

国家863项目(2014AA06A610)；物化探所所长基金项目(AS2013J07)

陈实(1982-)，男，助理工程师，现主要从事软件工程以及并行计算与三维可视化软件开发工作，E-mail:chen884488shi@126.com。

1001-1749(2015)04-0416-06

P 631.3

A

10.3969/j.issn.1001-1749.2015.04.02