基于Park变换的单相光伏并网控制研究

王亮，王志新，陆斌锋

（1.上海交通大学电气工程系，上海 200240；2.嘉兴清源电气科技有限公司，浙江嘉兴 314031）

基于Park变换的单相光伏并网控制研究

王亮1，王志新1，陆斌锋2

（1.上海交通大学电气工程系，上海 200240；2.嘉兴清源电气科技有限公司，浙江嘉兴 314031）

近年来，LCL滤波器由于体积小、滤波效果好等优点在光伏并网系统中获得了广泛应用。采用并网电流、电容电流双闭环控制能够有效抑制LCL滤波器振荡，提高并网系统稳定性，但传统PI控制无法实现对交流并网电流的无静差跟踪。因此，提出了一种基于Park变换的双电流闭环控制策略，它能够大大提高并网功率因数，减小入网电流的总谐波失真（THD）。该方法首先通过构造虚拟正交电流分量，将单相并网电流虚拟为α-β坐标系下两相正交电流，然后基于Park变换，在旋转坐标系下进行PI控制，从而实现无静差控制。最后，通过Matlab仿真验证了这种控制策略的正确性和有效性。

并网控制；Park变换；单相光伏系统；LCL滤波器；PI控制

1 引言

随着新能源发电技术，如风力发电、光伏发电和燃料电池发电等越来越受到人们的重视，对并网发电逆变技术的关注也日益增加［1］。在并网系统中，如何提高入网电流功率因数、减小入网电流总谐波失真（THD）成为当前研究的热点问题。

由于电感小、开关频率低、高频谐波衰减效果明显等优点，LCL滤波器在光伏并网系统中获得了广泛应用。但是，LCL滤波器为3阶系统，可能发生谐振导致系统不稳定［2-3］。作为目前最成熟的解决方法之一，采用电容电流内环的双电流闭环控制能够有效抑制谐振发生，保证入网电流的功率因数，因此得到了广泛研究［4-6］。在双电流闭环控制系统中，电流外环控制器一般PI控制，但其无法对交流信号进行无静差跟踪。文献［7］将准比例谐振控制引入外环控制器中，能够在特定频率产生很高增益，从而实现无静差跟踪，但其硬件实现复杂。本文对采用LCL滤波器的单相光伏并网控制器进行分析，在电网电流外环、电容电流内环的双环控制系统基础上，通过构造虚拟正交电流，在电流外环对电网电流进行Park变换后采用PI控制，从而达到无静差的控制效果。

2 系统模型及分析

图1为采用LCL滤波器的单相光伏并网逆变主电路。其中，Udc为直流输入电压，u为逆变器输出电压，i1为逆变器侧电感电流，ic为电容电流，ig为并网侧电感电流，ug为电网电压。

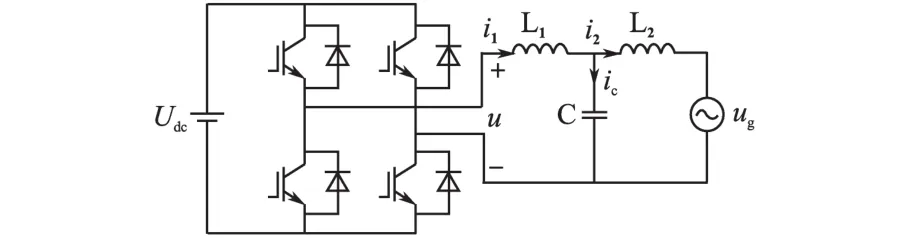
图1 单相光伏并网逆变主电路Fig.1 Single-phase photovoltaic grid-connected inverter circuit

采用P，PI或PID控制器直接对并网电流ig进行电流单闭环控制是不稳定的［8-9］。因此，需要引入滤波电容电流内环控制，增大系统的阻尼，削弱谐振尖峰，从而提高系统稳定性。同时，为了达到无静差控制，本文在并网电流外环构造虚拟正交电流分量，通过Park变换在旋转坐标系下采用PI控制。系统的控制框图如图2所示。

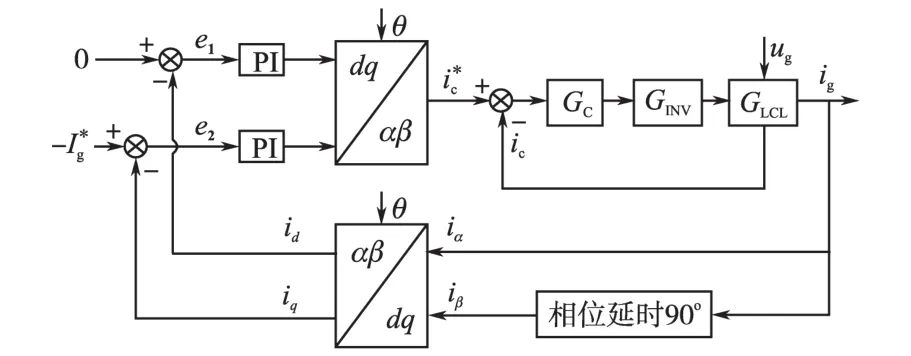
图2 系统控制框图Fig.2 System control model

图2中，LCL滤波器的控制框图如图3所示。忽略滤波电感和电容的寄生电阻，G1=1/sL1，G2=1/sC，G3=1/sL2。

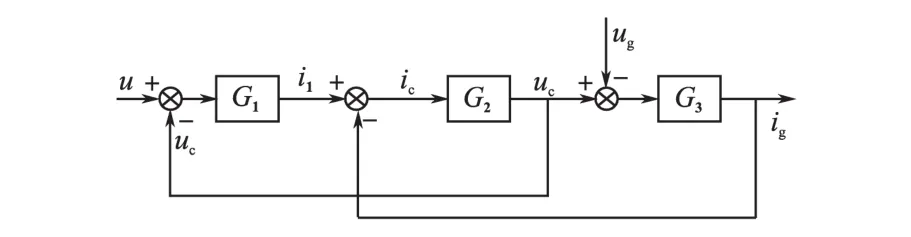
图3 LCL滤波器控制框图Fig.3 Control model of LCL filter

在单相光伏并网系统中，并网电流ig只有一相，因此在Park变换前，需要构造并网电流ig的虚拟正交电流分量。首先，取并网电流ig作为两相静止坐标系下的iα分量，不考虑谐波，设为

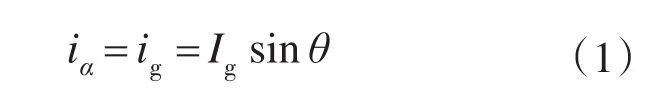
式中：Ig为入网电流峰值。

将并网电流ig延时90°作为ig分量，即

将iα，iβ经过Park变换后，得到d-q旋转坐标系下的id，iq，采用的坐标变换矩阵为

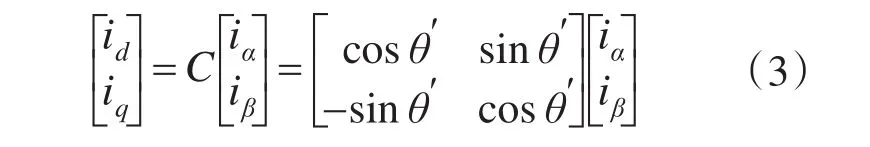
式中：θ′为电网电压ug通过锁相环（PLL）后得到的电网电压相角。

将式（1）、式（2）带入式（3），得：

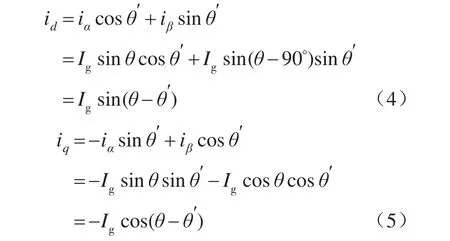
由式（4）、式（5）可知，当电网电压相角θ′和并网电流相角θ相等，即实现入网电流功率因数为1时，id，iq分量满足

上文表明，经过式（3）所示的坐标变换后，id表示电流无功分量、iq表示电流有功分量的相反数，从而在d-q坐标轴上实现了有功和无功的解耦控制。单相光伏并网系统通常要求入网功率因数为1，在d-q旋转坐标系下，对id，iq分别采用PI控制使之满足式（6）即可实现该目标，因此本文提出了图2所示的控制框图。

与式（3）对应的反Park变换为

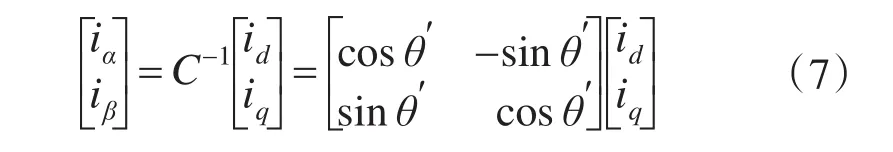
3 控制器设计

在电网电流、电容电流双闭环控制系统中，外环决定控制系统的调节精度，而内环确定系统的稳定性［10］。将电网电压视为外界扰动，不考虑其影响，由图2、图3推导出电流外环控制器输出到并网电流Ig的开环传递函数Gop1为

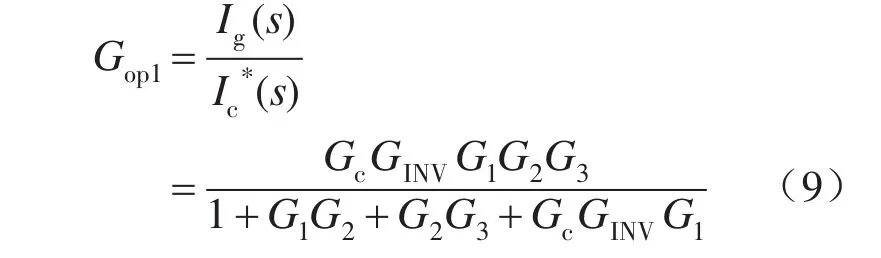
电流内环控制器Gc一般采用比例控制器，设Gc=kc。由于开关频率较高，逆变器可近似为增益GINV=kPWM。化简式（9）得：

由式（12）可知，电流内环是一个二阶系统，其阻尼系数为

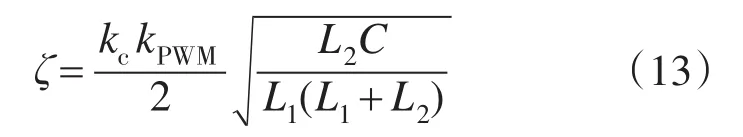
为了兼顾系统的阻尼效果和动态性能，一般取阻尼系数为0.707。根据式（13），就可以由滤波器参数求出内环控制器参数kc，本文取kc=0.15。

为了便于外环控制器参数设计，将Park变换后移，等效控制框图如图4所示。

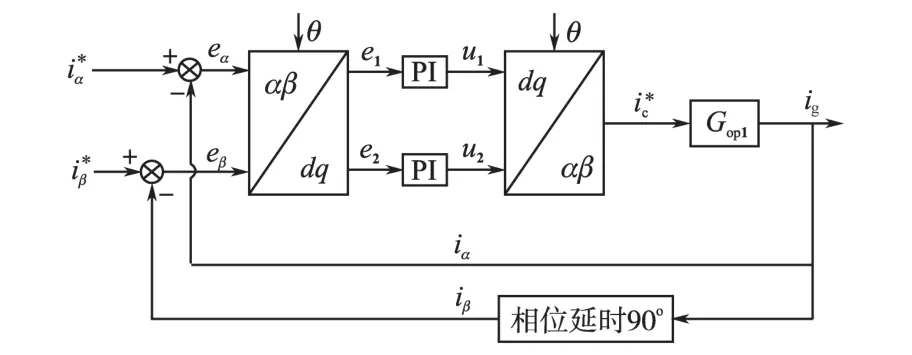
图4 等效系统控制框图Fig.4 Equivalent system control model

在图2中，PI控制器的输入为

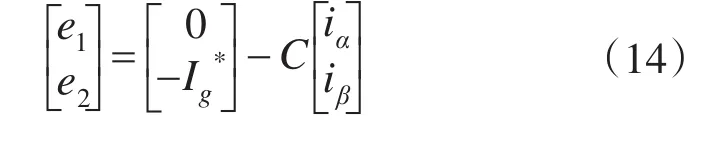
将Park变换后移之后，PI控制器的输入为

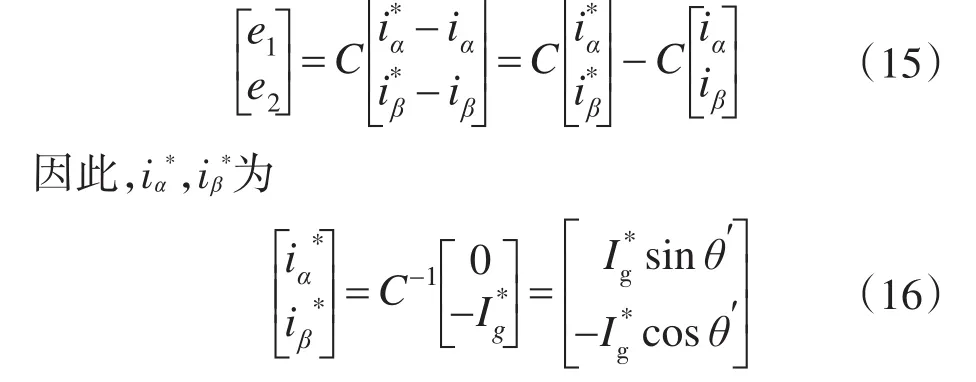
由式（16）可知，图2和图4所示系统是完全等效的。联合式（7）、式（8），可求得：

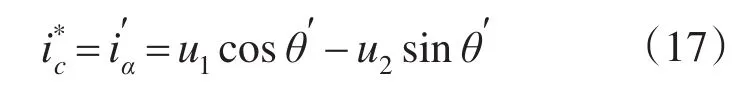
由于电网电压基本不变，可认为其相角θ′=ω0t，其中ω0为电网角频率。将式（17）两边同时进行Laplace变换，且由频移特性得：

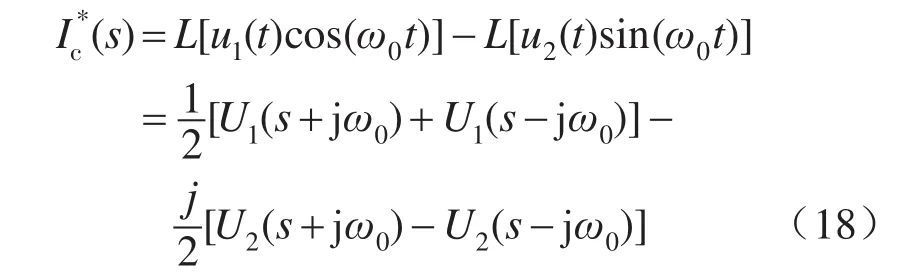
电路参数对称，故d-q坐标系下的2个PI控制器参数都取为

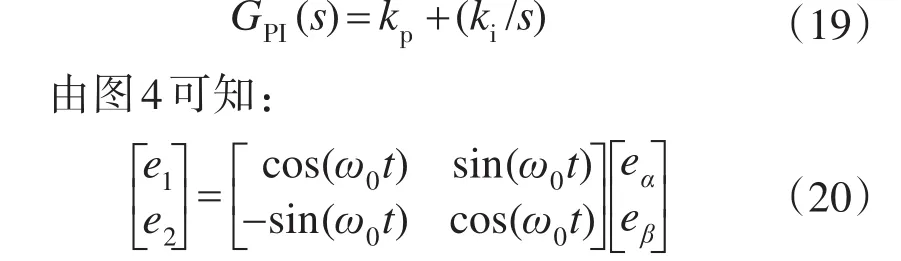
同理，对式（20）进行拉氏变换，得：

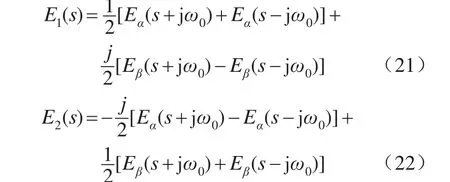
又由图4和式（19）可知：

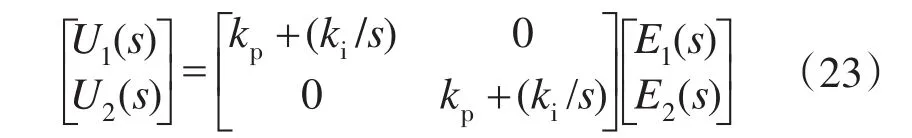
将式（21）、式（22）带入式（23）后，再带入式（18），求出，即

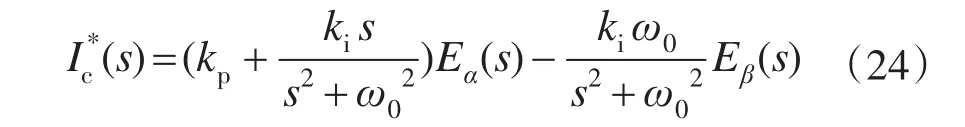
从式（24）可以看出，经过Park变换后，有功部分PI控制器的传递函数与比例谐振控制非常相似，因此可以采用比例谐振控制器的设计方法选取控制参数。经过调试，最终确定控制参数kp=1.15，ki=100。

4 仿真实验

为了验证理论分析的正确性，本文在Matlab/Simulink环境下搭建仿真模型，仿真参数为：直流母线电压Udc＝400 V，电网电压幅值ug＝380 V，电网频率fs＝50 Hz，给定并网电流幅值I*g＝6 A，开关频率fk＝20 kHz，逆变器侧电感L1＝3.3 mH，滤波电容C＝5 μF，电网侧电感L2＝2 mH。

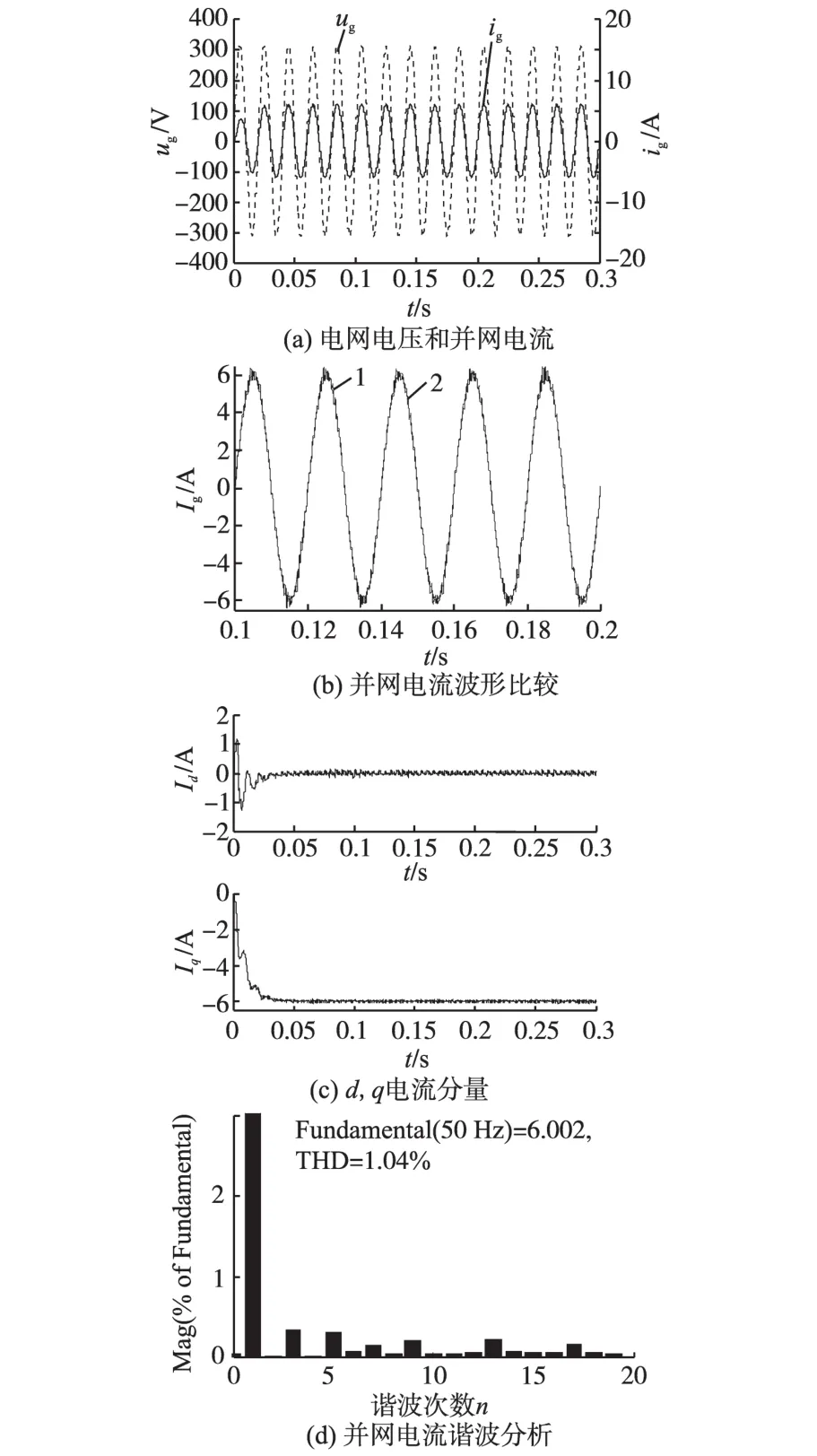
图5 仿真结果Fig.5 Simulation results

仿真结果如图5所示。其中，图5a为电网电压和并网电流波形，可见输出并网电流波形非常接近正弦波，而且和电网电压相位相同，保证了入网功率因数接近为1。图5b中，曲线1为基于Park变换双闭环下的并网电流，曲线2为常规双闭环控制下的并网电流，比较发现两者波形基本一致。但采用常规双闭环控制时，并网电流在峰谷值点及其附近会产生0.3~0.4 A的偏差；而在基于Park变换的双闭环控制下，并网电流始终能够跟踪给定正弦电流，在峰谷值点附近没有波动产生，且大小总为6A。图5c为旋转坐标系下，并网电流的d轴和q轴分量。系统稳定后，Id接近于0 A，Iq接近于-6A，只存在非常小的波动，与上文对控制系统的分析完全吻合。图5d为并网电流的频谱分析，并网电流基波分量为6.002 A，THD=1.04%<5%，满足电流幅值控制要求和电能质量要求。

5 结论

在采用LCL滤波器的单相并网逆变器中，由电容电流反馈和并网电流反馈构成的双电流闭环控制能够有效增加系统阻尼，提高系统稳定性。经过Park变换后，并网电流给定值在d-q坐标系下的旋转分量都是直流量，因此在该坐标系下，PI控制器能保证网侧电流的功率因数，并达到无静差控制的效果。

［1］ 沈国桥，徐德鸿.LCL滤波并网逆变器的分裂电容法电流控制［J］.中国电机工程学报，2008，28（18）：36-41.

［2］ 白志红，阮新波，徐林.基于LCL滤波器的并网逆变器的控制策略［J］.电工技术学报，2011，26（1）：118-124.

［3］ 徐志英，许爱国，谢少军.采用LCL滤波器的并网逆变器双闭环入网电流控制技术［J］.中国电机工程学报，2009，29（27）：36-41.

［4］ Liserre M，Blaabjerg F，Hansen S.Design and Control of an LCL-filter-based Three-phase Active Rectifier［J］.Industry Applications，IEEETransactionson，2005，41（5）：1281-1291.

［5］ 刘飞，段善旭，查晓明.基于LCL滤波器的并网逆变器双环控制设计［J］.中国电机工程学报，2009，29（S1）：234-240.

［6］ 王要强，吴凤江，孙力，等.带LCL输出滤波器的并网逆变器控制策略研究［J］.中国电机工程学报，2011，31（12）：34-39.

［7］ 周林，冯玉，郭珂，等.单相光伏并网逆变器建模与控制技术研究［J］.太阳能学报，2012，33（3）：485-493.

［8］ Twining E，Holmes D G.Grid Current Regulation of a Three-phase Voltage Source Inverter with an LCL Input Filter［J］.IEEE Transactions on Power Electronics，2003，18（3）：888-895.

［9］ 郭小强，邬伟扬，顾和荣，等.并网逆变器LCL接口直接输出电流控制建模及稳定性分析［J］.电工技术学报，2010，25（3）：102-109.

［10］彭双剑，罗安，荣飞，等.LCL滤波器的单相光伏并网控制策略［J］.中国电机工程学报，2011，31（21）：17-24.

修改稿日期：2014-12-13

Research on Controller of Single-phase PV Grid-connected System with Park Transformation

WANG Liang1，WANG Zhi-xin1，LU Bin-feng2
（1.Department of Electrical Engineering，Shanghai Jiaotong University，Shanghai200240，China；2.Jiaxing Renewable Power Electrical Co.，Ltd.，Jiaxing314031，Zhejiang，China）

LCL filter is widely used in PV grid-connected system for its small volume and excellent filter characteristic in recent years.Dual-loop control strategy with grid current feedback and capacitor current feedback can inhibit resonance effectively and improve system stability.However，the traditional PI controller cannot track the AC grid-connected current without static error.Thus，a dual-loop control strategy based on Park transformation was proposed，which could improve the power factor and reduce the THD.Firstly，the virtual orthogonal component was created to constitute theβcurrent while the grid-connected current constitutes theαcurrent.After Park transformation，the static error was inhibited by PI control.Finally，the Matlab simulation results verify the correctness and availability of the designed control strategy.

grid-connected control；Park transformation；single-phase PV system；LCL filter；PI control

TM464

A

国家自然科学基金项目（51377105）；国家863计划项目（2014AA052005）；嘉兴市科技计划项目（2014BZ15002）

王亮（1991-），男，硕士研究生，Email：tjuwangliang@gmail.com

2014-07-08