探究解题规律，渗透类比思想

☉上海市桃浦中学 张正丽

探究解题规律，渗透类比思想

☉上海市桃浦中学 张正丽

一、引言

在高三复习课的教学中，笔者认为教师要关注和激发具有生命活力的课堂，不能只是为了讲题而讲题，决不能重复“昨天的故事”——让学生在题海战中感觉数学学习的艰难.教师在教学中要充分挖掘模拟题的“可探究性元素”，注重揭示知识的本质，让学生感悟到数学知识之间的联系，以期达到“解一题，会一类，通一片”的目的.

二、问题展示

（2015年徐汇二模理14）如图1，点P（x，y）（x＞0，y＞0）是双曲线学用以下方法研究|OM|：延长F2M交PF1于点N，可知△PNF2为等腰三角形，且M为F2N的中点，的焦点，M是∠F1PF2的平分线上一点，似地：如图2，点P（x，y）（x＞0，y＞0）是椭0）上的动点，F1、F2是椭圆的焦点，M是∠F1PF2的平分线上一点，且___.

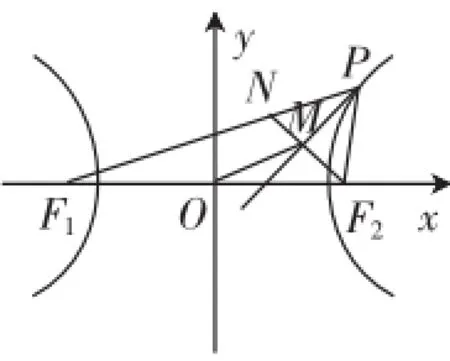
图1

图2

以上是高三复习圆锥曲线专题时的一道练习题.学生在解题过程中出现了困惑：（1）如果题目中没有给出双曲线中研究|OM|的方法，那么很多学生根本就不会证明“|OM|=a”；（2）为什么双曲线中|OM|求出的是一个定值，而在椭圆中求的是|OM|的取值范围，并不是一个定值？

为解决学生的困惑，笔者设计了探究椭圆与双曲线的性质的类比的一节课.为帮助学生更加直观解释曲线本质上的内在联系，使用了几何画板辅助教学，揭示椭圆与双曲线的定义的区别与联系，并通过解题方法上的类比，触类旁通，开启探索的智趣，打开学生思维的大门，探究解题规律，渗透类比的思想方法.

三、教学过程

（一）课前完成梳理两种曲线的基本知识

名称椭圆双曲线定义平面内到两定点F1、F2的距离的和为常数（大于|F1F2|）的动点的轨迹叫椭圆，即|MF1|+|MF2|=2a＞|F1F2|平面内到两定点F1、F2的距离的差的绝对值为常数（小于|F1F2|）的动点的轨迹叫双曲线，即||MF1|-|MF2||=2a＜|F1F2| y y图像O x Ox图3图4焦点在x轴上时：x2a2+y2 b焦点在x轴上时：x2a2=1焦点在y轴上时：y2a标准方程2=1焦点在y轴上时：y2a 2-y2b2=1 a、b、c的关系a2=c2+b2，a＞0，b＞0 c2=a2+b2，a＞0，b＞0 2+x2 b2= 1 2-x2b

设计意图：引导学生领会椭圆和双曲线的定义与标准方程的差别仅在“和”与“差”上，抓住矛盾的两个方面，为后面将椭圆与双曲线进行类比作铺垫.

（二）用类比思想探究椭圆、双曲线的性质

（1）证明此命题为真命题.

（2）你能否类比到双曲线上，给出一个类似的命题？并证明.

（1）证明：延长F2P与F1Q的延长线相交于点N，则QP为F2N的垂直平分线，|QF2|=|QN|.又|QF2|+|QF1|=2a，则|F1N|=2a.

又OP为△F1F2N的中位线，所以|OP|=a.

即点P在以O为圆心、半径为a的圆上.（如图5）

图5

证明：延长F2P交F1Q于点N，故|QF2|=|QN|.

由双曲线的定义得|QF1|-|QF2|=2a，

11

所以点P在以O为圆心、半径为a的圆上（.如图6）

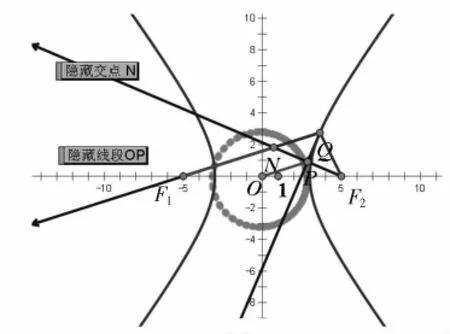
图6

设计意图：（1）强化求动点轨迹的严格推理论证的过程，巩固椭圆和双曲线的定义；

（2）由“外角平分线”类比为“内角平分线”的过程比较困难，让学生小组讨论、大胆猜想；

（3）在论证的过程中引导学生观察、分析、归纳、总结，得出类比不是简单的生搬硬套，必须注意两者的定义的区别；

（4）几何画板动画演示，增强直观感觉，体验猜想、类比失败之后的成功感.

（1）猜想结论，并证明；

（2）类比到双曲线中，写出一个类似的命题，并证明之.

图7

证明：同上，略.

图8

设计意图：（1）探究过程可以从特殊位置开始，猜出结论，再进行一般论证；

（2）类比到双曲线时，引导学生根据两个曲线的定