初中数学慢教育的“数据化”特点分析

☉江苏省连云港市教育科学研究所 孙朝仁

☉江苏省连云港市海庆中学 朱桂凤

·江苏省连云港市孙朝仁名师工作室

初中数学慢教育的“数据化”特点分析

☉江苏省连云港市教育科学研究所 孙朝仁

☉江苏省连云港市海庆中学 朱桂凤

数学慢教育作为一种“过程”教育的方式，从属于哲学实践范畴.慢教育的过程既是“漫溯长篙”的实践过程，又是“为快而慢”［1］提升学力的过程，这双重逻辑过程的叠加突出慢教育过程的“数据化”特点，即情感过程目标数据化、问题过程层次数据化、思维过程概念数据化、逻辑过程复合数据化.本文以“关键教学事件”为例，分析数学慢教育“四化”特点，展现慢教育“生命感”的本体价值.

一、情感过程目标数据化——一种“协商意识”倾向

情感作为学习活动发生的心理基础，类属于认识论范畴.情感是认知活动的起跳板，认知是情感作用的结果，积极的情感态度能让认知水平呈正态分布.而认知情感增长率取决于协商意识作用下的尊重程度，协商能让消极情感正向逆转、积极情感线性上升，终归于认知目标的有效达成.换句话说，就是协商意识倾向可以获得积极认知情感，数据化认知目标是情感作用的外在表现.数学课程总体目标中指出，数学思考、问题解决、情感态度的发展离不开知识技能的学习，知识技能的学习必须有利于其他目标的实现.这就要求我们借助协商意识助推认知情感增值，实现目标数据化的课程目标，落实慢教育课程“情感态度”价值观（见表1）.

表1 ：课程情感态度目标描述框架

为落实情感态度课程目标，我们研制了适合慢教育课堂特点的情感认知目标数据化的指标体系（见表2）.

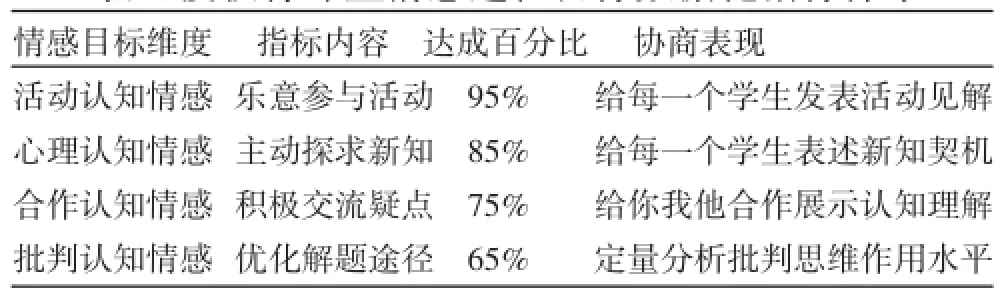
情感目标维度指标内容达成百分比协商表现活动认知情感乐意参与活动95%给每一个学生发表活动见解心理认知情感主动探求新知85%给每一个学生表述新知契机合作认知情感积极交流疑点75%给你我他合作展示认知理解批判认知情感优化解题途径65%定量分析批判思维作用水平

为引领数学慢教育课堂情感认知目标实践路径，现以“平行”开课模块为实施样例（见表3），显化慢教育“协商意识”倾向及其在认知情感层面的效度.

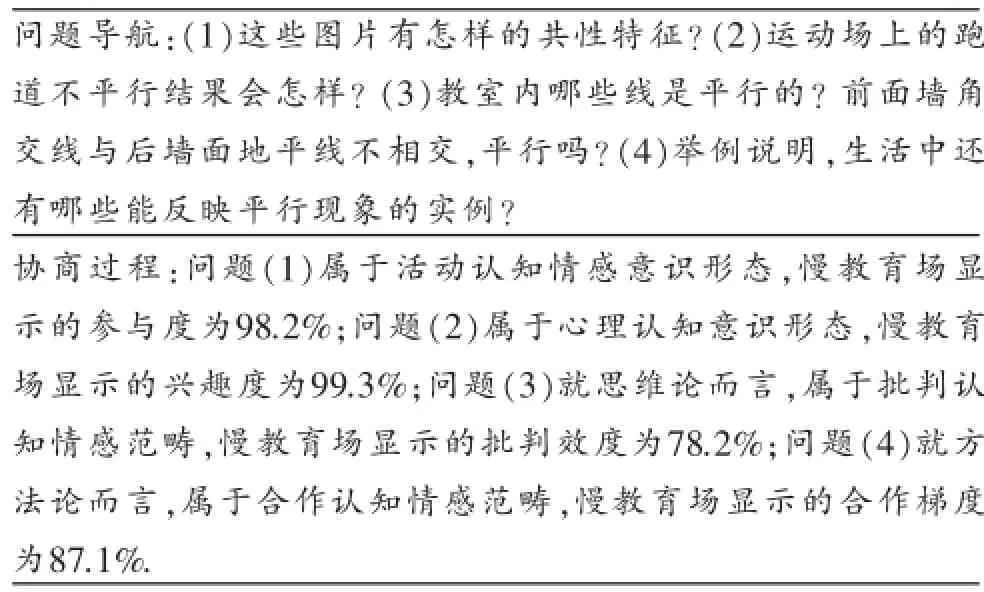
表3 ：慢教育课堂情感过程目标数据化实践样例（平行）

表2纵向反映情感认知目标的4个子维度，横向体现该维度下指标内容、协商表现及其应有的数据界定.表3反映具体问题导航指南和协商行为及其数据化收集过程.表2指标的研制为表3的实践提供行动框架，表3的工作成效反作用于表2指标的内在机能.因此，认知情感指标随工作成效的变化而变化.这与弗洛姆“师生双主体论”［2］所追求的目标是主动性（Initiative），而不是主体性（Subjectivity）的变化观具有共同指向.

二、问题过程层次数据化——一种“多元意识”倾向

问题作为思维的研究载体，从属于哲学意识范畴.问题过程的本质就是显化问题的来龙去脉及其发生、发展的思维脉络.慢教育课堂的问题过程“层次化”反映多元教育意识倾向，是观照“个体”生命思维特征的特殊性表现，终归于不同的人在数学上得到不同发展的课程理念.《义务教育数学课程标准（2011版）》把发现和提出问题的能力、分析和解决问题的能力作为“四能”目标，并以政策文本的形式写进课程.这就要求我们在慢教育理念支配下，关注问题意识的培养，方能实现“求知欲”到“求识欲”的立体变迁，进而基于“多元化”思想落实“问题解决”课程教育目标（见表4）.事实上，提出问题是创造思维的开始，就这个层面而言，提出问题比解决问题更重要.这与郑毓信教授的“问题解决”思想意旨一脉相承.［3］

表4 ：课程问题解决目标描述框架

为落实问题解决课程目标，我们研制了适合慢教育课堂特点的问题过程层次数据化的指标体系（见表5）.

表5 ：慢教育课堂问题过程层次数据化指标体系

为示范数学慢教育课堂问题解决过程的层次性，现给出以“拼图”实验模块为研究载体的实施样例（见表6），以此突出慢教育“多元意识”倾向及其在提出问题层面带来的效益.

表6 ：慢教育课堂问题过程层次数据化实践样例（拼图）

表4纵向反映“问题解决”的4个层次维度，横向体现该维度下指标内容、多元表现及其应有的数据界定.表5反映问题具象过程中多元化表现以及数据的统计处理.表4指标的研制为表5的生态运行指明了正方向，表5运行的结论为表4框架指标研制的可行性及修正方向提供事实证据.事实上，“问题层次指标”与“多元化过程”的内部关系反映了马克思的哲学观，即主体和客体是认识论中的一对哲学概念.“主体”是具有意识和意志的人，“客体”是指主体以外的客观世界，是主体的认识和客观对象，终归于认识与实践的本体关系.［4］

三、思维过程概念数据化——一种“联系意识”倾向

思维作为物质语言外壳，类属于方法论范畴.从信息加工学角度来看，思维是对感知记忆的信息进行加工得出新信息的过程.据此，可以把“过程性”思维概念理解为孕育“前概念”的过程及其共同特征的归结.而归结本身就带有明显的联系意识倾向，概念数据化的过程就是定量联系具体化的过程，因此，联系意识对思维概念的形成起着积极的支配作用.在数学课程中，应当重视学生的数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力和模型思想，这是数学“课程标准”对教学实施的要求，不难发现十大“核心词”的作用目标直指基于联系的概念行为.因此，慢教育课堂作为共性中的个性，势必在联系的思维平台上把握概念性思维过程，方能落实“数学思考”课程目标（见表7）.

表7 ：课程数学思考目标描述框架

为落实数学思考课程目标，我们研制了适合慢教育课堂特点的思维过程概念数据化的指标体系（见表8）.

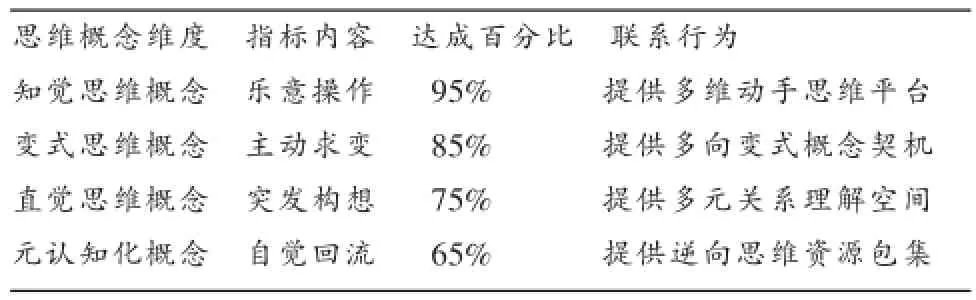
表8 ：慢教育课堂思维过程概念数据化指标体系

为体现数学慢教育课堂数学思考过程的概念性，现呈现“中点四边形”实验模块实施样例（见表9），以此凸显慢教育“联系意识”倾向及其在概念学习层面发挥的作用.

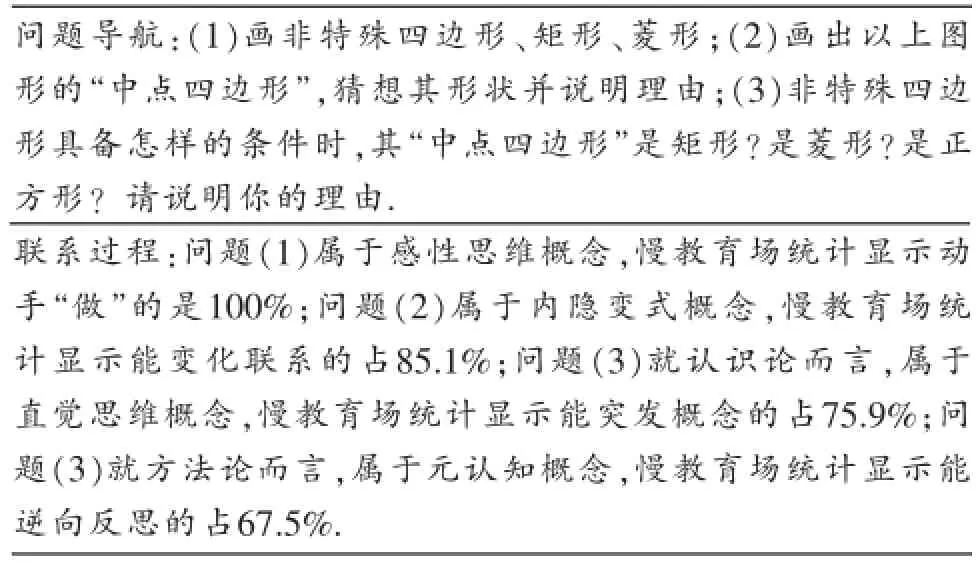
表9 ：慢教育课堂思维过程概念数据化实践样例（中点四边形）

表8纵向反映“数学思考”的4个概念性维度，横向显化该维度的指标内容、联系行为及其应有的数据性界定.表9反映“联系观”支配下具体概念思维的发生、发展过程，以及数据的整理定性过程.表7具有宏观统领作用，表8具有中观指导作用，表9具有微观示范意义.

四、逻辑过程对象数据化——一种“共生意识”倾向

“逻辑”是事物内部关系的一种表现，其作为数学教育严密的科学形态，类属于逻辑思维学范畴.“抽象”是逻辑过程的起点，在信息加工学中，以言语信息加工为主流的抽象思维过程就是逻辑过程对象数据化的具体表象.《数学形象思维心理元素》［5］一文指出，视知觉本身已具备抽象概括的功能，数学表象具备抽象特征.数学慢教育课堂以视知觉思维活动最为突出，这就揭示了慢教育逻辑过程对象的实质（共生意识）.“课程标准”重视让学生体验从实际背景中抽象出数学问题、构建数学模型、寻求结果、解决问题的过程.这就要求我们设计“好问题”，让学生在逻辑关系中实现知识技能的正迁移，进而落实慢教育过程性“双基”课程教育目标（见表10）.

表10 ：课程知识技能目标描述框架

为落实知识技能课程目标，我们研制了契合慢教育课堂特点的逻辑过程对象数据化的指标体系（见表11）.

表11 ：慢教育课堂逻辑过程对象数据化指标体系

为显化数学慢教育课堂知识技能逻辑过程路径，现给出“探索三角形全等的条件”实验模块实施样例（见表12），彰显慢教育“共生意识”倾向及其在逻辑思维层面带来的心理效应.

表12 ：慢教育课堂逻辑过程对象数据化实践样例（探索三角形全等的条件）

表10纵向反映逻辑对象的4个维度，横向反映该维度的指标内容、共生行为及对应的数据界定.表11反映逻辑过程框架内数学对象产生式系统的形成过程.表10体现课标双基精神的指导作用，表11体现数学慢教育课堂逻辑框对象架体系，表12是对慢教育逻辑过程的具象与解释.

数学慢教育“数据化”特点，既是对数学认知过程的概括，又是对“超回归”模型的聚类分析.［6］反映数学认识论与方法论、思维学与逻辑学的交互作用，超越慢教育本身“慢”的意义.

1.朱桂凤，孙朝仁.数学慢化教育的元话语与操作要义［J］.中学数学（下），2014（10）.

2.弗洛姆.自为的人［M］.北京：国际文化出版公司，1988.

3.郑毓信.数学教育科研之关键性论题与发展趋势［J］.数学教育学报，1998，7（4）.

4.马克思.马克思恩格斯全集（第46卷）［M］.北京：人民出版社，1979.

5.何小亚，朱华伟.数学形象思维的心理元素［J］.数学通报，1993（10）.

6.李淑文，张同君.“超回归”数学理解模型［J］.数学教育学报，2002，11（1）.Z