关联：建立模型的有效策略

☉江苏省如皋市石庄镇初级中学 蔡晓严

关联：建立模型的有效策略

☉江苏省如皋市石庄镇初级中学 蔡晓严

模型思想是《义务教育数学课程标准（2011年版）》（下称《标准（2011年版）》）提出的十个核心词之一，模型思想的建立是学生体会和理解数学与外部世界联系的基本途径．因此，在初中阶段的数学教学中，我们应重视模型思想的渗透，让学生经历建立模型、求解模型的过程，充分体会模型思想的价值．在近期的中考一轮复习课上，笔者将模型思想渗透在审题教学之中，抓住题目中的关键信息，将文本、图形与数学模型紧密关联在一起，形成了问题解决的快速通道．现结合部分教学片断谈一些体会，希望能给您带来一些启示．

一、紧扣基本概念，提取解题模型

数学概念是数学模型的生成基础，不同的数学概念一般会生成与之配套的模型．因此，在解题教学中，我们可以抓住题中的基本概念，利用基本概念与数学模型的关联，努力从已有的知识结构中提取出与之匹配的解题模型，铺平问题解决的道路．

案例1“概率”复习片断.

例1在三只乒乓球上，分别写有三个不同的正整数（用a、b、c表示）．三只乒乓球除上面的数字不同外，其余均相同．将三只乒乓球放在一个盒子中，无放回地从中依次摸出两只乒乓球，将球上面的数字相加求和．当和为偶数时，记为事件A；当和为奇数时，记为事件B．设计一组a、b、c的值，使得事件B发生的概率为并说明你的正确性．

教师：认真阅读例题，想一想，这道题目要我们做什么？

教师：怎么解决这个问题呢？

学生2：因为是概率问题，所以，我们可以用树形图或表格来列举出所有等可能的结果，然后根据所列结果，选择合适的数据验证结论．

教师：好的，树形图是化解概率问题的一个很好的模型，接下来，大家就用这个模型来解决这道题目．

（学生自主解答，教师巡视指导，并请一名学生在黑板上画出树状图，给出了完整的解题过程）

教师：非常棒！树状图和表格是我们列举概率事件结果的模型，在解决概率问题时经常用到．用好这两个与“概率”相关的模型，我们就可以顺利化解一些较为复杂的概率问题了．

案例分析：在学生学习“概率”时，不仅知道概率的基本含义，还深入学习了概率的求法，尤其对与之紧密关联的用以列举事件发生结果的“树状图”与表格这两种数学模型有了较为深刻的认识．在解答概率问题时，这两种数学模型是学生最容易想到的，而且也是化解现阶段概率问题最有效的方法．所以，教者充分利用学生已有问题解决的经验，让他们从审题入手，理清例题的解题目标，将“概率”这一基本概念与认知结构中的解题模型（树状图、表格）关联起来，以与基本概念匹配的解题模型的应用推动有效的解题过程的形成．

二、用好符号替代，形成常用模型

在数学问题中，一些未知的数量在题目中是显性存在的．在例题教学中，我们应努力将未知量与未知数关联起来，引导学生将这些能够直接看出的未知数量用未知数x，y直接“代入”，抽取出指向问题解决的数量关系，从而得出一些常用的数学模型，如方程（组）、不等式（组）等．

案例2“方程组的应用”复习片断.

例2小明和小丽到文化用品商店帮助同学们买文具．小明买了3支笔和2个圆规共花19元；小丽买了5支笔和4个圆规共花35元．每支笔多少元？每个圆规多少元？

教师：题中有哪些未知数量？

学生1：笔的单价和圆规的单价．

教师：如果我们设每支笔x元，每个圆规y元．将x和y“代入”到题目中，你发现了什么？

学生2：3x和2y共19元；5x和4y共35元．

教师：你是怎么发现的？

学生3：直接将x，y分别代入到题中笔和圆规的位置上，就可以发现这样的关系了．

（在学生叙述过程中，教师用红色粉笔将题中的“笔”和“圆规”分别用x，y“代入”）

教师：很好！说说你的解题模型吧！

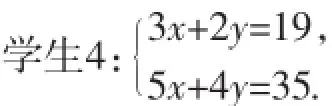
教师：真不错！请大家给出完整过程．

案例分析：在应用题解答中，方程（组）和不等式（组）是学生常用的数学模型．案例2中，教者抓住题目的特点，让学生用“符号替代”的方式发现题中存在的数量关系建构方程组．从问题解决的角度看，教师的引导和学生的探究是成功的，解题模型的顺利得到让接下来“给出完整过程”成为可能．而上述探究与交流的过程，不仅提取了学生脑海中“等量代换”的经验，还将等量代换由“同质代换”（代换的内容相同，比如同为文字）演变为“异质代换”（符号代替文字），找到了一条建构常用数学模型的快速通道．

三、定格特殊位置，获取几何模型

“图形与几何”是义务教育阶段的重要学习内容．学生在学习这一版块知识时，会将一些蕴含着丰富数学知识的几何图形定格为几何模型，融入到已有的知识网络中，比如角平分线模型、垂直平分线模型等．这些几何模型，不仅指向几何知识本身，还与方程、函数等数学模型有着密切的联系，是学生化解一些综合问题的“利器”．

案例3“相似三角形”复习片断.

例3如图1，在四边形ABCD中，AD∥BC，∠ABC=90°，AB=8，AD=3，BC=4，点P为AB边上一动点，若△PAD与△PBC是相似三角形，则满足条件的点P的个数是（）.

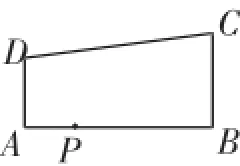
图1

A．1个B．2个C．3个D．4个

教师：请同学们认真阅读题目，并找出题中可能存在的数学模型．

学生审题，标记并作图．5分钟后，全班交流．教师：说说你们的发现吧！

学生1：我发现图中存在“一线三直角”模型．

教师：哦！是吗？

学生2：是的．根据题意可得，在△PAD和△PBC中，∠A＝∠B＝90°．如果△PAD与△PBC是相似三角形，那么，顶点A和顶点B一定是两个三角形的对应顶点．如图2，∠DPA＝∠PCB．易得，∠DPC与∠A、∠B一样都是直角．

教师：很好！这就是“一线三直角”模型，还有其他模型吗？

学生3：我发现的也是“一线三直角”模型，如图3，这时，点P的位置离B点近了些．

学生4：我觉得这道题中不光有“一线三直角”模型，还有“光线反射”模型．除了直角外，我觉得两个三角形中的点P也可以是对应顶点．如图4，此时∠DPA＝∠CPB，这实际上类似于物理上的“光线反射”模型，此时两个三角形同样是相似的．

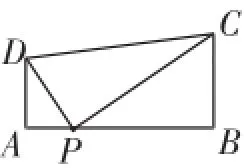
图2

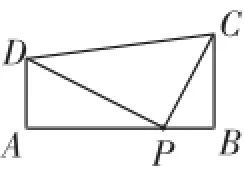
图3

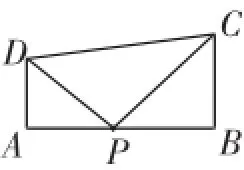
图4

教师：真不错，你还将物理模型移植到了数学上来了！这两种看似不同的数学模型，我们能归为一类吗？

学生5：都叫“K形图”吧！

教师：嗯！确实都像，就叫“K形图”吧！那么，这道题中符合要求的点P一共有几个呢？

学生（齐答）：3个！

案例分析：在学生的数学认知活动中，几何图形因其直观性，成为学生最容易接受的数学模型，成为他们解决几何问题的重要工具.案例3中，教师让学生从探究P点位置入手，挖掘题中可能存在的数学模型，“一线三直角”模型、“光线反射”模型，以及最终归纳得出的“K形图”，学生不仅关注了“形”上的相似，还理清了这些模型的知识起点和数学道理，为这一模型在今后解题中的应用扫清了障碍.这样的教学，以例题求解为抓手，突出解题一般方法的呈现，将模型思想渗透到教学之中，发展了学生的创新意识和应用意识，提升了学生分析问题和解决问题的能力.

四、抓住关键词语，建构组合模型

初中阶段，数学题的信息呈现方式很多.不仅有纯文本信息，还有图形信息、图像信息和表格信息.虽然信息的呈现方式不同，但我们只要抓住其中的关键信息，就可以建构出有效的解题模型.为此，我们在教学中应注意培养学生捕捉关键信息的能力，并引导学生将关键信息与数学模型关联起来，提升他们问题解决的能力.

案例4“一元二次方程”复习片断.

3.模型的产出。模型的产出主要是一系列计算结果,这些结果基于模型的投入和假设条件,经过相关财务公式计算而来。主要的结果包括:资本支出;削减股本;提取债务;服务费(对于特许经营权项目为车辆通行费);其他运营收入(对于特许经营权项目表现为次级收入,如特许经营权公路相邻的土地开发收入);运营支出;利息;税;偿债;(收入)损益表;资产负债表;现金流(现金来源和使用);贷款方的债务偿还能力比率(流动比率,利息偿付比率,债务与股本之间的比率等);投资者的回报;净现值(以便公共主管部门能够对不同投标进行比价)等。

例4t是实数，若a，b是关于x的一元二次方程x2-2x+t-1=0的两个非负实根，则（a2-1）（b2-1）的最小值是_________.

教师：题目告诉我们哪些信息？

学生1：一元二次方程x2-2x+t-1=0，这个方程有两个非负实根a，b.

教师：那这道题要我们求什么？

学生2：（a2-1）（b2-1）的最小值.

教师：这题用什么数学模型来求解？哪些词能引导你发现解题模型？

学生3：最小值，我感觉可能与“带范围的一次函数或二次函数”有关；a，b是两个非负实根，我觉着还可能与“根与系数的关系”有关.

教师：到底是不是这些模型呢？大家先试着将式子（a2-1）（b2-1）变形，速度快的同学可以试着去解一解.

学生4：通过变形，（a2-1）（b2-1）=（ab）2-（a+b）2+2ab+1.

教师：你们得到的是这个结果吗？

学生（齐答）：是的！

教师：那接下来，该怎么办呢？

学生5：根据根与系数的关系，可以得到a+b=2，ab= t-1.代入变形后的式子可得（a2-1）（b2-1）=t2-1.显然，这是一个二次函数，与学生3猜想的数学模型是一致的.所以，只要求出这个函数的顶点坐标就可以得到它的最小值了.

学生6：他说得不对！这个二次函数的顶点（0，-1），不在取值范围内！

教师：哦！是吗？

学生7：是的！根据“a，b是两个非负实根”，不仅能得到根与系数的关系式，还能得到：①Δ≥0；②a+b＞0；③ab＞0三个不等式，进而可以求出t的取值范围为1≤t＜2，这一段取值恰好在抛物线的对称轴的右侧.所以，当t取1时，函数可以取得最小值为-3.

教师：太棒了！那么，题中究竟是哪些关键词语对你建立模型具有提示作用呢？

学生8：“两个非负实根”告诉我们很多信息，既有根与系数的关系，又有根的判别式，还有不等式（组），我们应该先将能得到的模型写下来，然后在选择使用.

学生9：题中的“最小值”，告诉我们问题与函数有关，应该是函数图像的最低点.

教师：你们说的都很对！认真审题，将题中关键词语与解题模型关联起来，不仅是化解这道题目的有效策略，还是解决其他数学问题的很好的方法，希望大家在今后解题时要关注此法！

案例分析：在数学问题中，常隐藏着一些能够传递关键解题信息的词语.如果能将这些关键词语与常见数学模型关联起来，将有利于学生展开联想，形成有效的解题路径.因此，培养学生剖析关键词语的能力就应成为数学教学的重要任务.案例4中，教师引导学生从题中的“两个非负实根”和“最小值”入手展开联想，并尝试给出了函数、不等式（组）等解题模型组.这些模型建立在学生丰富的知识储备和解题经验之上，是对已有解题经验和数学模型重新整合，借用例题的讲评，教师将一些单一的数学模型和分散的解题经验逐步链接起来，形成了便于后面学习与应用的模型串.可见，基于关键词语剖析为起点的模型教学，应突出关键词语的发散联想，注重词语与模型的关联，让模型生成与审题析题同步.

数学模型来自于学生的数学认知活动，也服务于学生的认知活动.在学生的知识网络之中，数学模型既与数学的基础知识、基本技能有关，还与数学基本思想、基本活动经验紧密联系.因此，要想用数学模型解决数学问题，就应从问题本身入手，找寻出能够与模型关联的“关键点”，这些“点”可以是数学的基本概念，也可以是图形的特殊位置，或者是问题的关键词语.找到这些与模型紧密关联的关键信息，对学生从认知结构中提取出有用的数学模型是十分关键的.所以，我们应立足日常课堂教学，将模型思想渗透到每一个数学问题的解决之中，推动他们形成建构模型、应用模型的意识.H