简化数学高考解析几何试题运算的“三化与四策”

林新建

(漳州第一中学，福建 漳州 363000)

解析几何试题一直是数学高考的难点。它的难不在于向量的包装，也不在于几何条件的代数化，而在于运算。然而能力又恰恰体现在如何简化运算上，因此，简化运算便成了解决高考解析几何试题的重中之重了。那么，简化解析几何试题的运算有哪些方法呢?

一、解题方法巧用“三化”

(一)特殊化

特殊化是特殊与一般思想在数学高考解题中的具体应用。它是依据问题在一般情况下真则在特殊情况下亦真，反之，在特殊情况下不真则在一般情况下亦不真的原理——肯定某一结论或否定其余结论的解题过程。在解析几何中，善于运用特殊化方法，可帮助我们快速探明问题的解决方向，有效简化运算与求解途径。

例1(2009 年全国高考山东卷理科22 题)

(Ⅰ)求椭圆E 的方程;

(Ⅱ)是否存在圆心在原点的圆，使得该圆的任意一条切线与椭圆E 恒有两个交点A、B，且?若存在，写出该圆的方程，若不存在说明理由。

若满足条件的圆存在，设其方程为x2+y2=r2，由圆的任意一条切线与椭圆的两个交点A、B 均满足这个一般性结论可知，圆的某一条特殊切线，如x=r 与椭圆E 的两个交点A、B 必也满足，由此可将A(r，r)代入得，从而知若该圆存在，则圆的方程必为

确定出圆的方程，证明就是简单的事了，在这里，一般问题特殊化的数学思想引领起了决定性作用，凸显了特殊与一般思想在探索解题方向上的重要作用。

(二)极限化

极限化是有限与无限思想在数学高考解题中的具体应用。有限与无限相比，有限显得具体，无限显得抽象，对有限的研究往往先于对无限的研究。反之，当积累了解决无限问题的经验之后，可以将无限问题转化成有限问题来解决。这种有限变无限、无限化有限的解决数学问题的方法就是极限化方法，可以有效简化解析几何运算，轻松得到问题的答案。

例2(2011 年北京市高三质检考试题)

若双曲线x2-y2=a2(a ＞0)的左、右顶点分别为A、B，点P 是第一象限内双曲线上的点。若直线PA、PB 的倾斜角分别为α、β，且β=mα(m ＞1)，那么α 的值是( )

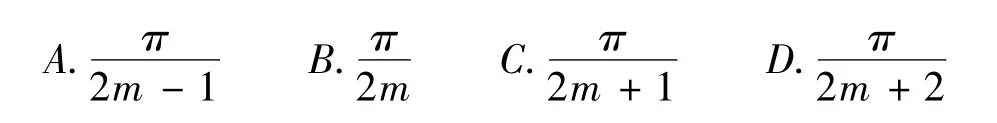
解析:本题求解若考虑坐标运算，需设出点P 的坐标，运用点P 的坐标满足双曲线的方程得到关于直线PA、PB 的斜率tanα、tanβ、所满足的关系式tanα·tanβ=1，进而将β=mα 代入，得到，所以α=。其实，本题作为一个选择题，若从思想去立意，运用极限化方法去无限逼近，则根本无需计算:

当P 趋向于无穷远时，直线PA、PB 趋近于直线PO，它们都趋近于渐近线y=x，此时m →1，验证选项即知正确答案为D。

这样解答，简单快捷，凸显了有限与无限相互转化在简化繁难运算上的巨大威力。

(三)坐标化

解析几何的本质思想是“用代数方法研究几何问题”，而坐标化方法正是这一重要思想在数学高考解题中的具体应用。对于给定的几何问题，若能巧妙运用坐标化方法予以建系求解，则能大大减少运算量，有效简化求解过程。

例3(2008 年高考江苏卷理科18 题)

解析:本题求解的常规方法是:设BC=m，∠ACB进而可求得其最大值为。以上方法思路直观但运算繁杂，解题不易进行，若能巧妙运用坐标方法予以求解，则可有效减少运算量，轻松快捷:

以AB 所在直线为x 轴，AB 的中垂线为y 轴建立平面直角坐标系。

设C(x，y)，由条件易得点C 的轨迹方程为(x-3)2+y2=8，从而

二、解题过程善用“四策”

(一)转换

转换是正难则反思想在数学高考解题中的具体应用。解题需要套路，看到这道题，你的第一反应是什么?迅速生成常规方案，也即第一方案。为什么要有套路?因为80%的高考题是基本的、稳定的，考查运算的敏捷性。没有套路，就没有速度。问题是，当实施第一方案遇到障碍时，我们的策略是什么?

例4(2006 年高考湖北卷理科20 题)

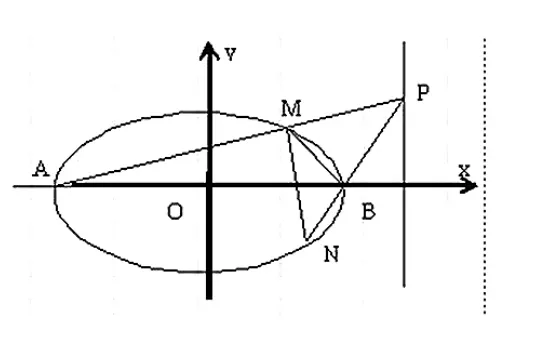
(Ⅰ)求椭圆的方程;

(Ⅱ)设P 为右准线上不同于点(4，0)的任意一点，若直线AP、BP 分别与椭圆相交于异于A、B 的点M、N，证明点B 在以MN 为直径的圆内。

处理难题，从方法论的角度讲就是转换视角。常态方案不行，换一个方案行了;这种说法与思路不通，换一个说法通了;在一个领域内繁复的问题，换一个领域简单了。对处理解析几何试题的繁难运算，自不例外!如若不是这样，靠什么考查能力?又凭什么说高考是一种选拔性考试呢?再如，

例5(2008 年高考全国卷Ⅰ理科21 题)

双曲线的中心为坐标原点O，焦点在x 轴上，两条渐近线分别为l1、l2，经过右焦点F 垂直于l 的直线分别交l1、l2于A、B 两点。已知成等差数列，且同向。

(Ⅰ)求双曲线的离心率;

(Ⅱ)设AB 被双曲线所截得的线段长为4，求双曲线的方程。

解析:本题难在第(Ⅰ)问，若考虑坐标运算，就得由渐近线方程与直线AB 的方程联立，求出A、B 的坐标，进而求得，再利用它们成等差数列的条件来解，其运算的繁难程度可想而知。

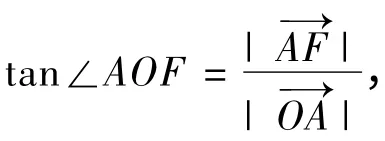
稍微一转换，便可充分利用平面几何的性质，从而避免了繁杂的坐标运算。这也正是我们在解析几何中经常遇到的问题:三种运算(坐标、向量、逻辑)，我们选择什么?特别是在实施运算过程中遇到障碍时，如何从思想立意去调整和转换运算?

(二)构造

构造是构造思想在数学高考解题中的具体应用。把转换作为求解解析几何问题的策略无疑是必要和合理的，它要求我们在简化繁难运算时必须具备转换意识，这样才能有效地解决问题。但是，转换并不总是永远畅通无阻的。正像走路一样，我们要迈向目的地(结论)，从起点(条件)出发，不断地变换方向和路径，从一处转向另一处逐渐向结论靠拢，但有的地方却无法过去，需要修筑道路，架设桥梁，这就需要构造。

例6(2010 年高考辽宁卷理科20 题)

解析:本题很难，难在运算，许多考生依常规设出直线AB 的方程，联立椭圆方程运用韦达定理消参，以期获得a、b、c 的关系式以求得离心率，结果均半途而废，望繁难运算兴叹而已。其实，若从思想上立意，构建出焦点三角形，便可运用椭圆定义予以求解，这样几无运算量，问题也可轻松获解。

设F'为左焦点，连AF'、BF'。设|BF| =m，则|AF| =2m，|BF'|=2a-m，|AF'|=2a-2m，∠AFF'=60°，∠BFF'=120°。

在△AF'F 和△BF'F 中，分别施行余弦定理，可得:

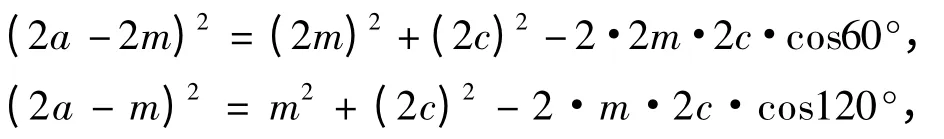
化简得:a2-c2=(2a-c)m，2(a2-c2)=(2a+c)m，消去m，即得

借助(Ⅰ)问，第(Ⅱ)问唾手可得:

(三)类比

类比是“类比思想”在数学高考解题中的具体应用。在解析几何中，若能根据两个对象在某些方面的类同之处进行类比，把信息从一个对象转移给另一个对象，可大大减少运算量，有效简化求解过程。

例7(2009 年高考辽宁卷理科20 题)

(Ⅰ)求椭圆C 的方程;

(Ⅱ)E，F 是椭圆C 上的两个动点，如果直线AE 的斜率与AF 的斜率互为相反数，证明直线EF 的斜率为定值，并求出这个定值。

解析:第(Ⅰ)问求椭圆方程，运用定义法求解可有效减少运算量，容易求得椭圆C 的方程为1。第(Ⅱ)问，设直线AE 的方程为代入并由韦达定理可得进而得到

注意到点F 坐标的计算与点E 有类同之处，所以可进行类比，只需将k 换成-k，即得，运用斜率公式即可求得kEF=为定值。

因为类比，我们减少了关于点坐标的计算，无疑为紧张的考试节省了宝贵的时间。

(四)化归

化归是“化归与转化思想”在数学高考解题中的具体应用。在解析几何中，若能有效运用化归的方法，可使繁难的运算化繁为简，化大为小，从而使问题轻松获解。

例8(2010 年高考北京卷理科19 题)

在平面直角坐标系xOy 中，点B 与点A(-1，1)关于原点O 对称，P 是动点，且直线AP 与BP 的斜率之积等于

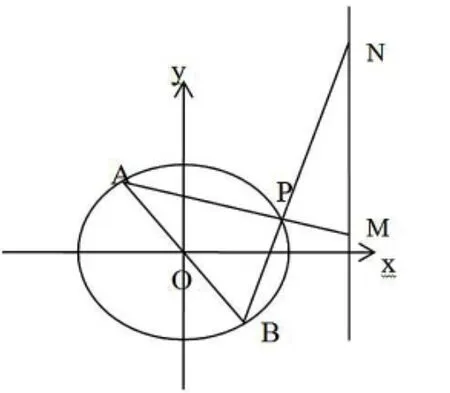
(Ⅰ)求动点P 的轨迹方程;

(Ⅱ)设直线AP 和分别BP 与直线x=3 交于点M，N，问:是否存在点P 使得△PAB 与△PMN 的面积相等?若存在，求出点P 的坐标;若不存在，说明理由。

难在第(Ⅱ)问，假设存在满足条件的点P(x0，y0)，由△PAB 与△PMN 的面积相等可得|PA|·|PB| =|PM|·|PN|，由于M、N 的坐标未知且不易求得，许多考生至此束手无策，望运算兴叹而已。

怎么办?稍作转化，将|PA|·|PB| =|PM|·|PN|转化为，再化归为，容易解得，代入即可求得

若作以下化归转化，则几乎不用计算:

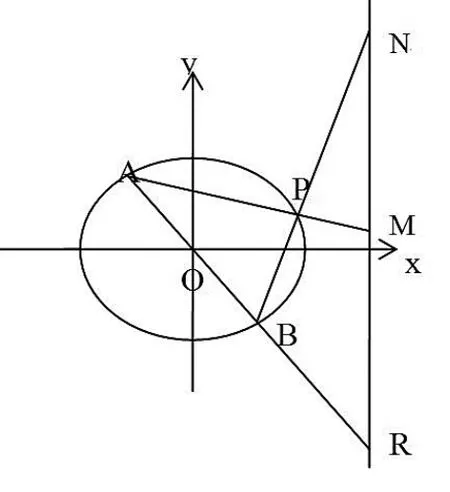
延长AB 交直线x=3于R，则△PAB 与△PMN的面积相等这一条件可转化为△AMR 与△BRN的面积相等。由于A 到直线x=3 的距离为4，B 到直线x=3 的距离为2，从而知即M 为NR 中点。又B 为AR 的中点，所以P 为△ARN的重心，从而，代入椭圆方程即可求得

本题求解还可将△PAB 与△PMN 的面积相等这一条件化归转化为△ABM 与△NBM 的面积相等，进而转化为直线AN 与BM 平行两直线斜率相等，读者不妨一试。

因为转化，我们将繁难的解析几何运算进行得如此简单!否则，我们做什么?

以上是笔者就数学高考解析几何试题的运算简化策略所作的探析，这些方法具有较强的操作性，但怎样想到运用这些方法，则需要思想立意。学生怕数学，很重要的一个原因在于数学的繁难运算，只要我们树立运用思想引领解题的意识，运算就会变得很简单，解题就能做到举重若轻、挥洒自如。

［1］林新建.从高考试题谈新课程数学复习的“六性”［J］.数学通报，2010(10).

［2］陈元章，林新建.新课程数学高考复习的辩证之道［J］.数学通报，2013(7).

［3］林新建.从2009 年高考试题谈复习教学的八个关注［J］.中学数学研究，2010(1).