紧扣目标 跟进生成 综合应用——基于小学数学教学中多媒体使用不当的思考

黄荣楣

(宁德市蕉城区实验小学，福建 宁德 352100)

一、紧扣目标，做到有的放矢

1.症状:重形式轻内容

目前，仍然可以看到这样一种倾向:在一些评优课、公开课或者参赛课上都使用了多媒体教学手段，甚至把它当作课堂教学的一种“时髦”。于是每当评优课、公开课或赛课时，上课教师便会云集电脑高手，殚精竭虑，酣战数日，方才磨出一“剑”(课件);在课堂上，也可处处见缝插“机”，即使是几道口算题甚至是课本上的练习题，也都要用多媒体来辅助，甚至课题板书，也要用多媒体一字一字滑稽地显示出来……

2.把脉开方:紧扣教学目标，用在关键处

这种集声、像、动漫与图文并茂一体的教学，学生在课堂上看起来热热闹闹，师生对答如流，可实际教学往往只是形式化、表演化。因此，教学时应注意以下几点:一是紧扣教学目标。多媒体教学虽然有无可比拟的优势，但是，我们也不要忘记了，多媒体教学只是为课堂教学达到最优化的一种辅助手段，而非最终目的。教学时，如果只看形式，或本末倒置，或画蛇添足，课堂效益一定大打折扣。因此，在多媒体的使用上一定要紧紧围绕教学目的，摒弃与教学目标无关的内容。二是用在关键处。在备课前要多考虑能否帮助学生更好地理解知识的重点、难点、疑点，能否帮助学生解决传统教学所无法达到的效果，能否提高学生的学习积极性，只有注重形式与内容的完美结合，才能最大限度发挥多媒体的优势作用。例如:教学苏教版五年下册《解决问题的策略——转化》一课中，课后有一道这样的习题:用分数表示图中涂色部分。学生在思考后，大多数学生的答案是9/16，因为他们认为涂色部分是一个正方形，边长是3 格，把图形旋转过来面积就是9格。教师不急于评价，让其他学生发表意见，此时很快有学生指出:

正方形的边长不可能是3 格，因为其中一个空白部分形成一个直角三角形，直角边是3 格，斜边一定大于它。(根据学生回答，师闪烁两条边)许多学生恍然大悟，教师再次演示课件，果然正方形旋转后大于9 格。那么该怎么表示呢?

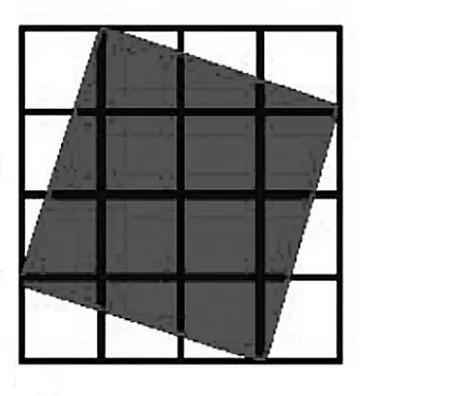
学生出现了不同的思考方法:①把涂色部分分解成四个直角三角形(底3 高1)和一个边长2 格的正方形，并把三角形两两相拼。②先算出图中空白部分所占的方格数，再推算出涂色部分。(根据学生回答，课件展示不同的方法)最后一致得出涂色部分有10 格，用分数5/8 表示。在上述教学教程中，教师能充分结合学生的思考，用“闪烁”“旋转”等方法，让学生清晰看出9/16 的错误所在，又通过“割”“拼”等动作演示，让学生直观理解转化的不同方法，课件使用恰到好处。

二、跟进生成，做到真正交互

1.症状:重预设轻生成

在使用课件的课堂上，如果留心就不难发现:教师为了方便操作，往往把一堂课的知识点按照教师备课的方案来设定程序，一般采用线性结构的方式制作课件，课件“播放”完了，课也就结束了。如:一位教师在教学梯形面积公式的推导时，引导学生小组讨论:“能不能应用我们已学过的知识来推导梯形的面积公式呢?”正当这位教师运用课件演示梯形公式的推导一帆风顺，准备进入课堂练习时，下面有的学生举起来手来，有的学生在说:“还有其他方法来推导。”教师只好叫这些学生来说，有的学生说:“把一个梯形沿中间剪成两个梯形，再拼成一个平行四边形也能推导出它的面积公式。”有的学生说:“我是用两个完全一样的直角梯形拼成一个长方形来推导。”……由于这位教师课件只设计一种方法，而没有设计这些学生“另类推导”的环节，只好说:“你们的想法都很好，下课后我们再讨论。”然后再继续下面的教学环节，而那些有自己见解的学生也只好师命难违地坐了下来。

2.把脉开方:充分预设，用好交互动能

这种一键定乾坤，完全按照教师设定的程序进行教学，学生的思维只能在教师的预设之中无法偏离，即使有了偏离，教师也会想方设法把学生引导到既定的轨道上来，学生如果有所生成，课件中没有设计，只能用“你们的想法都很好，下课后我们再讨论”以进入下一个环节的教学。这样使用多媒体教学，使教学预设扼制了课堂的生成，课堂没有生成，哪来的精彩?这样的教学流程反而成了“独木桥”，试想这样长此以往的教学，怎么能有效地培养学生的创新能力?怎么能调动学生上课积极动脑、积极举手发言的积极性呢?因此，教学时应注意以下几点:一是要充分预设。多媒体课件的制作应充分发挥传统教学所不可比拟的优势，要让多媒体教学服务于教学目标，要尽量多考虑学生所能想到的都设计进去，要设计留给学生思考的时空，学生发表见解的机会，能适应学生不同的活动参与进来。二是使用具有交互功能的软件，如“交互式电子白板”等，既可教师演示，又可根据课堂生成让学生动手操作，增强其交互性。但也不可能奢求多媒体能满足课堂的所有需要，因为课件的设计无论交互性怎样强，其变化规则也是可预见的，而课堂上学生的生成是不可预料的，所以课堂上还得以教师为组织者、主导者，多媒体只是一个“辅助者”，不能越俎代疱。只有这样，才能让教学智慧之火燃烧在课堂教学之中。

三、综合应用，实现有效探究

1.症状:重演示轻操作

有些数学教师看到了多媒体的众多优势，往往用课件的演示代替学生的操作，认为这样更直观、更形象。如有的教师在讲“圆锥的体积”公式的推导时，就把用“倒沙子验证”的过程拍成录像，在课堂上轻点鼠标，学生注目观看，无须动手，“等底等高，圆锥的体积是圆柱的三分之一”的演示过程就这样“轻松”地走完了。

2.把脉开方:注重操作，做到综合运用

上例中，如果让学生亲自动手操作，学生在不断“倒”的过程中，发现有的圆锥倒了两次就倒满圆柱，有的不行，有的圆锥倒了三次就倒满圆柱，有的不行……最后学生再比较圆锥与圆柱的底与高时，才发现“只有在等底等高的情况下，圆锥体积才是圆柱的三分之一，圆柱体积才是圆锥的三倍。”这样学生不仅能信服，同时又培养学生动手操作能力与解决实际问题的能力。由此可见，如果不注重操作，不做到综合运用多媒体，学生的探究能力、提出问题、分析问题、理性思考的能力都难以提高，数学课就很难上出“数学味”。

［1］斯苗儿.基于教学设计，把微课融进日常课堂——关于微课在小学数学课堂中应用的几点思考［J］.小学数学教育，2014(11).

［2］姚焕娇.小学数学课堂教学中动态生成的跟进策略［J］.新课程:小学，2009(3).

［3］童燕娜.“灵魂”跟进“智慧”常在——我区乡镇小学数学教师课时目标设计与实施情况的调研报告［J］.小学教学参考:综合版，2012(11).