磁流变阻尼器拉索减振系统的参数优化研究
龚 禹
(广东泛珠勘察设计有限公司,广东 广州 510630)
0 前言
洞庭湖大桥是连接华容和岳阳的一座大跨度公路桥梁,于2000 年建成完工并开始运营,为我国首座三塔型、双索面PC 斜拉桥,索间距为8.0 m,全桥设计拉索共布置222 根。由于洞庭湖大桥所处的地理位置风力较大,风雨共现时间长,加之拉索具有的光滑表面,具备了发生风雨振的条件,北方寒潮来临时都会引起大桥拉索风雨振,最严重时单边振幅超过40 cm。
国内外学者越来越关注斜拉索风雨振现象及其振动控制,对拉索减振方面进行了许多研究,提出了多种减振技术,其中最直接、最有效的拉索振动控制方法是增加拉索的阻尼,而目前增加拉索阻尼常用办法是在拉索和桥面间安装阻尼器,如磁流变阻尼器。磁流变阻尼器由高科技亚纳米材料-磁流变体制造的一种智能装置,可通过调节磁场强度,改变其阻尼特征,来实现控制阻尼力大小的输出,获得理想阻尼力来改变拉索的模态阻尼比,对于不同参数的拉索,采用同一型号阻尼器都能使每根拉索都达到最优的减振效果。
陈政清教授等[1-4]设计制作了永磁调节式磁流变阻尼器;禹见达等[5,6]根据磁流变阻尼器力学性能的试验结果,建立了非线性参数模型,很好地模拟了阻尼力的滞回特性;进行阻尼器减振系统的优化设计,使减振效果达到最优,磁流变阻尼器的优化设计主要考虑两个因素:一方面是阻尼器的安装位置,另一方面是磁流变阻尼器的阻尼系数。由于斜拉索本身所处位置的限制,阻尼器的安装高度位置会受到一定程度上的限制,从桥梁整体的美观上面考虑,减振器的在拉索上的安装高度不宜定的太高,设计运营中一般取拉索长度的2%~4%这个范围内,所以需要确定的因素主要是减振器的阻尼系数。
本文根据试验得到的磁流变阻尼器力学特性,然后根据阻尼器拉索减振设计方法,对减振系统进行了参数优化,主要计算了阻尼器的安装高度,确定了永磁调节式磁流变阻尼器的最佳档位。
1 永磁调节式磁流变阻尼器力学特性
本文研究的对象为永磁调节式磁流变阻尼器,在洞庭湖大桥拉索减振中得到了实际应用,是一种双出杆式阻尼器,试验中使用的MTS—810 试验机如图1 所示。

图1 MTS—810 试验机及原理图
通过MTS—810 疲劳试验机获得的永磁调节式磁流变阻尼器在振幅2.5 mm、频率1.0 Hz 下,4 个不同档位下阻尼器的力与位移、速度滞回关系曲线分别如图2 所示。
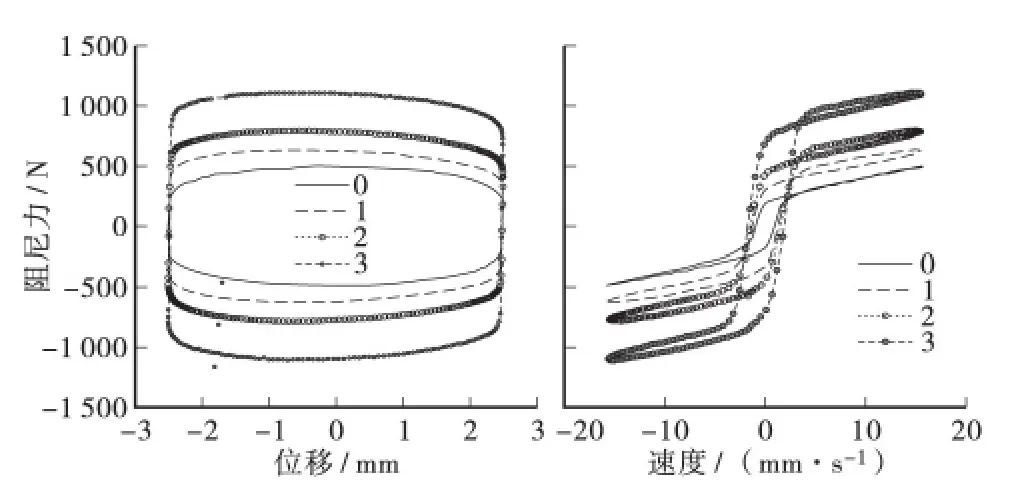
图2 不同档位下得到的磁流变阻尼器滞回曲线(f=1.0 Hz,A=2.5 mm)
由图2 可知:磁流变阻尼器的力学特性中滞回曲线比较光滑饱满,可见其耗能减震效果好;且随着阻尼器档位的变化增加,滞回曲线围成的面积增加;从力与速度的关系曲线可以看出,屈服后阻尼力与速度的关系基本上呈正比。
2 拉索-阻尼器优化设计理论
Kovas(1982)提出了斜拉索阻尼器减振系统的一阶模态阻尼比的优化设计方法。对于阻尼器减振系统,当阻尼器的阻尼系数C=0 时,则模态阻尼为0,而当阻尼器的阻尼系数为C=∞时,减振器就只起到了固定作用,相当一个固定支点,这样拉索的模态阻尼同样等于0。故在这两极限状态的范围内,一定存在一个相对优化阻尼系数Copt,使拉索减振系统会获得一个最大的模态阻尼比。

式中:ω01为拉索无阻尼基频;L 为拉索长度;xd为阻尼器距锚固点距离;m 为拉索每米质量。
Pacheco(1993)[7]在上述基础上推导了考虑多阶模态的阻尼器优化设计问题,提出了粘性阻尼器设计的归一化曲线,该曲线能根据阻尼器粘性系数确定模态阻尼比或针对某个模态取得最优阻尼比来确定阻尼器粘性系数,得到如图3 所示的优化设计曲线。
该曲线可用下面的一个多项式组成:


图3 Pacheco 阻尼器统一设计曲线
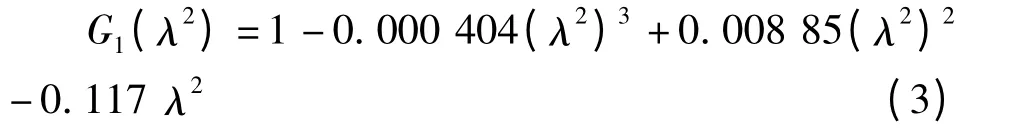
式中:EA 为抗拉刚度;θ 为倾角;T0为初始拉力。
这样,修正后的Pacheco 设计曲线为:

3 确定最优档位
永磁磁流变阻尼器的优化设计就是确定优化档位,使拉索模态阻尼比达到最优。根据修正的Pacheco 设计曲线,对第i 阶模态,阻尼器优化阻尼系数为:

为了增加阻尼力和防止拉索的面外振动,通常在拉索上对称于面内安装2 个阻尼器。假定拉索面内振动位移幅值为A,则阻尼器的位移A1可表达为:

式中:α=90°-β/2(β 为两阻尼器夹角)。

式中:Ceq为单阻尼器情况下位移振幅为A 时的等效阻尼系数。
这样永磁磁流变阻尼器的等效粘性阻尼系数:

根据实际拉索的参数m,T0,L,ω01,θ,λ2,xd/L,安装两个阻尼器,及两阻尼器间夹角α,由此可以确定磁流变阻尼器所需要的档位大小。如表1。

表1 所需档位
4 阻尼器安装的最小高度确定
阻尼器安装高度与拉索获得的模态阻尼比成正比,安装高度越高,能获得的模态阻尼比越大,但阻尼器安装高度过高会影响桥梁美观,同时也增加安装难度和成本,考虑桥梁美观要求和安装方便,安装高度考虑不超过2.0 m,对安装高度为0.5、1.0、1.5、1.8 和2.0 m 这5 种情况进行了计算分析。
阻尼器优化阻尼系数为Copt=0.10 mLω01/(ixc/L),在该阻尼系数下可获得的最大模态阻尼比为ξimax=0.52(xc/L),其中xc为阻尼器安装处距下锚固端的距离,m;L 为拉索长度,m。通过分析可知,安装阻尼器后,拉索获得的模态阻尼比与阻尼器阻尼系数、阻尼器安装相对高度等因素有关,同时施工质量也会影响拉索实际模态阻尼比,综合这些因素,拉索安装阻尼器后获得的实际模态阻尼比可表示为:
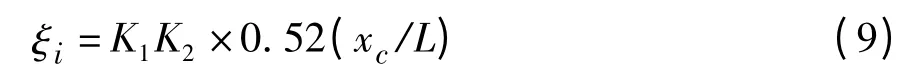
式中:K1为阻尼器阻尼系数影响参数,通常取0.6;K2为阻尼器安装质量影响系数,根据经验取0.7。
相应的前3 阶可获得最大阻尼比如表2 示。可以看出,当安装高度为0.5 m 时,第1 阶模态的可获得的最大阻尼比略小于要求的设计值;但是对于高阶模态,安装高度为1.5 m 时就能满足要求。由于垂度的影响,主要由第1 阶模态来决定最小的安装高度。

表2 S22 拉索阻尼器设计

图4 不同安装高度时拉索阻尼比
可以发现,最优阻尼系数随着安装高度和模态阶数的增加而减小。对最长S22 号拉索,阻尼器的安装高度确定为1.8 m,总的等效阻尼系数范围为86 ~258 kN/(m·s-1)。对拉索S1 ~S22,如图4 所示在阻尼器安装高度分别为0.5、1.0、1.5、1.8 和2.0 m 时,拉索获得的最大阻尼比与工程要求设计值的比较。可以看到阻尼器安装高度为0.5 m 时,部分拉索可获得的最大阻尼比是不能满足设计要求的;当安装高度为1.0 m 时,对S1 ~S22 号索只能基本满足设计要求;当安装高度为1.5 m 时,所有拉索均能满足应用要求。为了经济和美观,选择在拉索原减振系统中6 ~10 号索阻尼器安装高度距桥面1.5 m,10 号以后的长索安装高度为1.8 m,升级改造方案将利用原有系统的立柱,因此阻尼器安装高度不变,新增60 根拉索安装高度采用1.5 m。
5 结论
通过MTS—810 疲劳试验机对永磁调节式磁流变阻尼器试验与分析,获得以下主要结论:
1)获得了永磁调节式磁流变阻尼器的力学性能力与位移、速度滞回曲线。
2)得到了实际拉索所需的最低档位,计算了阻尼器的所须的安装高度,证明了磁流变阻尼器是拉索减振的可行的、有效的手段。
[1]Z Q Chen,X Y Wang,Y Q Ni and J M Ko.Field measurements on wind-rain-induced vibration of bridge cables with and without MR damper[C].Proceedings of the Third World Conference on Structural Control(ed.F Casciati),Como,Italy,April,2002:393-402.
[2]王修勇,陈政清,倪一清,等.斜拉桥拉索磁流变阻尼器减振技术研究[J].中国公路学报,2003,16(2):52-56.
[3]Z Q Chen,X Y Wang,J M Ko,Y Q Ni.MR damping system for mitigating wind-rain induced vibration on Dongting Lake cablestayed bridge[J].Wind and Structures,2004,7(5):293-304.
[4]陈政清.永磁调节装配式磁流变阻尼器[P].中国发明专利公报,CN:1 632 345A.
[5]禹见达,陈政清,曹 宏,等.永磁调节式MR 阻尼器试验研究及工程应用[J].振动工程学报,2006,19(4),532-536.
[6]禹见达,陈政清,王修勇,等.磁流变阻尼器的非线性参数模型[J].振动与冲击,2007,26(4):14-17.
[7]Pacheco,B.M.,Fujino,Y.and Sulekh,A..Estimation curve for modal damping in stay cables with viscous damper[J].Journal of Engineering Mechanics,1991,119(6):1961-1979.

