波形钢腹板预应力混凝土简支梁的剪力偏载系数研究
李茂良
(湖南湘潭公路桥梁建设有限责任公司,湖南 湘潭 411104)
0 引言
大量研究表明,普通混凝土腹板箱梁的抗弯刚度、抗扭刚度较强,且截面的整体性较好[1]。在偏心承载过程中,普通混凝土腹板箱梁的截面扭转引起的应力相比于其平面弯曲产生的应力较小,且箱梁结构中混凝土腹板与横隔板的厚度较大,从而导致偏载引起箱梁的畸变应力更小[2]。因此,在一般情况下,混凝土腹板箱梁不易发生扭曲破坏,同时在偏心承载过程中,混凝土腹板箱梁通常采用设置经验偏载系数的方法来考虑其偏载效应[3]。
波形钢腹板箱梁是以1 mm 左右的钢板替代40~90 cm 厚的混凝土腹板,相应减轻了自重,增强了抗剪能力[4]。由于波形钢腹板的结构较薄,相应其截面抗弯刚度、抗扭钢度和挠曲刚度存在一定程度的降低,当受到偏心荷载作用时,其箱梁的截面扭转或畸变产生的应力均较大,从而致使截面所承受的应力大大增加,因此,对其箱梁偏载系数的计算考虑具有重大实用意义[5]。而目前关于波形钢腹板预应力混凝土简支箱梁偏载系数的计算暂无准确的方法,一般采用混凝土腹板箱梁的偏载系数的方法进行计算[6]。因此,为确保波形钢腹板预应力混凝土简支箱梁的安全,本文结合某高架桥工程实例,采用有限元对其关键截面的偏载系数进行分析,同时通过对比,总结出该桥梁的偏载系数分布规律,研究结果可为波形钢腹板预应力混凝土简支箱梁桥计算的偏载系数合理取值提供重要的参考依据。
1 偏心荷载作用下的箱梁力学行为及偏载增大系数
在偏心荷载P 作用于箱梁结构过程中,其力学行为可根据其作用的效果分别定义为对称荷载P作用与偏心扭矩Pe 作用两种形式,则相应力学计算时需将偏心扭矩引起的扭转与对称荷载引起的箱梁截面弯曲进行计算[7]。通常正应力偏载增大系数ξ与剪应力偏载增大系数λ 可定义为:

式中:σ弯曲为对称荷载P 在截面上产生弯曲正应力;σ约束扭转为扭矩Pe 在截面作用产生约束扭转正应力;σ畸变为截面发生扭转产生的畸变正应力。

式中:τ弯曲为对称荷载P 在截面上产生弯曲和剪应力;τ约束扭转为扭矩Pe 在截面作用产生约束扭转剪应力;τ畸变为截面发生扭转产生的畸变剪应力。
2 偏心荷载作用下箱梁的应力相关计算方法
2.1 经验取值计算法
经验取值计算法一般适用于普通混凝土箱梁的应力计算,其计算过程中通常不考虑扭转变形引起的畸变应力,而是对偏载作用下引起箱梁扭转产生的扭转正应力与剪应力分别取值为对称荷载作用下平面弯曲的正应力的0.15 倍、剪应力的0.05 倍[8],同时结合对称荷载作用过程中所得相关的应力结果,可大概的计算出考虑扭转影响的总弯矩大小为:

式中:Me表示总弯矩;Mg表示恒载弯矩;Mp表示对称活载中心线作用时的弯矩。
大概的计算考虑扭转影响的总剪力大小为:

式中:Qe表示总剪力;Qg表示恒载剪力;Qp表示对称活载中心线加载时的剪力。
2.2 偏心压力法
该方法是将混凝土箱梁的腹板假设为开口截面的箱梁边肋,通过计算得出其梁肋的横向分配系数k 后,依据梁肋的总体数量进行乘积计算,可得到正应力偏载增大系数ξ。
2.3 修正偏心压力法
由于偏心压力法在计算过程中没有考虑到整体抗扭刚度,当箱梁的抗扭强度较大时,其实际计算所得的偏载增大系数结果准确性较低。因此通常需对偏心压力法进行修正计算。修正偏心压力法是将箱梁腹板假设为等截面的箱梁边肋,通过计算得出偏心活载作用时其箱梁边腹板的荷载分配系数,再将其与腹板的总体数量进行乘积计算,从而得出箱形截面的正应力偏载增大系数ξ[9]。通过修正偏心压力法可计算出总荷载的弯矩与剪力,其具体计算可描述为:

式中:Mm表示总弯矩;Mg表示恒载弯矩;Mp表示对称活载中心线作用时的弯矩;ξ 表示偏载增大系数。

式中:Qm表示总剪力;Qg表示恒载剪力;Qp表示对称活载中心线加载时的剪力;ξ 表示偏载增大系数。
综上所述可知:经验取值计算法因没有对截面的几何尺寸和荷载作用进行考虑,通过假定参数对总弯矩与总剪力进行计算,其得出的计算结果准确性较低,同时适用性较差。偏心压力法由于没有对箱梁的整体抗扭强度进行考虑,因此得出的计算结果比实际结果较大。偏心压力法与修正偏心压力法均将横梁刚度假定为无限大,因此当桥梁的宽度较大时,其相应刚度存在一定程度的较低,以致计算结果与实际的误差较大。此外,修正后的偏心压力计算法对箱梁的抗扭强度进行了考虑,同时是以闭合箱形截面假设为开口梁肋,因此在偏载作用时,与偏心压力法计算得出的截面剪力流具有本质区别。上述3 种方法均能方便快速的计算出混凝土箱梁截面偏载增大系数,但是运用于预应力混凝土简支箱梁计算时缺乏实际依据,且是否适用于波形钢腹板预应力混凝土简支箱梁的截面偏载增大系数的计算,仍需进一步研究。
3 工程概况及建模
3.1 工程概况
项目的桥梁梁体采用双箱单室波形钢腹板预应力混凝土简支组合箱梁结构,其中跨径为40 m,梁高为2.2 m,钢腹板厚度为0.12 m,同时为增加波形钢腹板PC 组合梁截面的抗扭刚度,在两端与跨间共设置7 道横隔板。其立面与横截面如图1 所示。
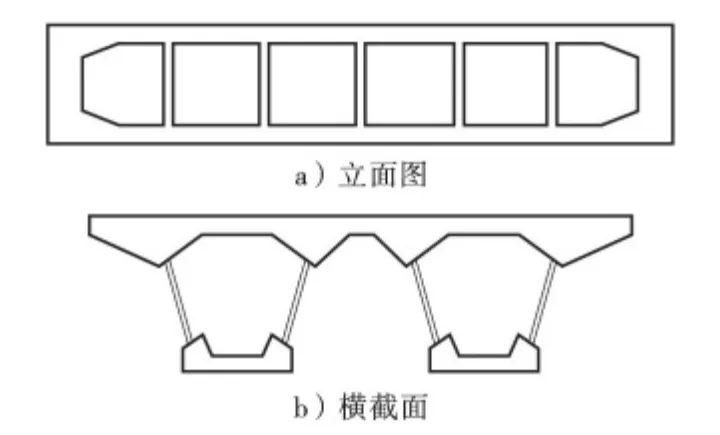
图1 桥梁的立面与横截面示意图
3.2 有限元模型建立
通过采用ANSYS 有限元的分析模块CBCW 建立波形钢腹板实体工程模型,同时运用节点自由度藕合法分别对波形钢腹板的接合部与预应力筋锚固端进行处理,首先建立实体初模型,然后进行网格的划分,最终形成有限元模型,如图2 所示。
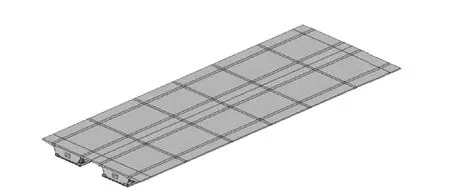
图2 桥梁的有限元计算模型
边界条件约束布置:根据该桥箱梁的结构两端为简支,将其两端支点的节点X(横向)和Y(竖向)的自由度均进行条件约束,而节点Z(纵向)的自由度只对其一端采取约束。荷载布置部分:由于桥梁结构的自重荷载和预应力荷载均属于对称恒载,且几乎不会影响到桥梁的偏心增大系数,因此本次试验不进行考虑,只将其作为初始状态,分别对活载在对称、偏心的两种工况进行模拟,并计算桥梁结构的偏载增大系数。其中活载根据《公路桥涵设计通用规范》的相关规定,并结合该桥梁的跨径,布置“均布+集中”形式的荷载,其均布荷载qk与集中荷载P 分别为10.5 kN/m、320 kN。具体荷载布置如图3所示。

图3 各荷载布置示意图
3.3 计算截面及测点布置
将波形钢腹板的箱梁分成9 个等截面作为本次试验的计算控制截面,其等截面分别为前墩、L/8、L/4、3L/8、L/2、5L/8、3L/4、7L/8、后墩。同时将底板偏载一侧角点位置设为正应力的测点,并将各控制截面波形钢腹板中点位置设为剪应力的测点。
4 截面剪力分担比例及偏载系数有限元分析
通过对波形钢腹板箱梁的有限元模拟与计算,分别得出活载在对称、偏心两种工况下的数据结果,将各控制截面测点的数据进行提取,并基于提取数据计算分析其剪力分担与偏载系数。
4.1 剪力分担比例分析
由于施加的剪应力沿波形钢腹板高均匀分布,故选取腹板中心点施加的应力大小作为此控制截面腹板剪应力数值,然后进行计算与分析,得出其剪力分担比例。通过选取对称活载作用在箱梁中9 个控制等截面腹板中点的剪力值,并对各控制截面腹板的剪力进行分担比例计算,具体如表1 所示。
根据表1 可知:当对称活载作用在波形钢腹板预应力组合梁时,其剪力分担比例范围在58.2%~80.6%之间,其中L/4 与3 L/4 位置的分担比例达到最大值,前后墩顶位置的分担比例为最小值。
对称活载作用下波形钢腹板各控制截面的剪力分担比例沿箱梁纵向的分布规律如图4 所示。由图可知:在简支梁桥中不同截面腹板的剪力分担系数不同,且近似沿梁中心向两侧对称分布。在墩顶附近时,截面腹板的剪力分担比例均小于其他截面,此时的分担比例为58.2%;在处于L/4 和3 L/4 位置时,截面腹板的剪力分担比例均大于其他截面,此时的分担比例为80.6%。造成简支梁纵向各截面的剪力分担比例分布不均匀主要与内衬混凝土和设置的横隔板有关,其中墩顶附近的截面由于存在波形钢板与内衬混凝土的组合腹板,因此腹板部分剪力由内衬混凝土分担;而位于横隔板附近的界面,其腹部部分剪力由横隔板分担。L/4 与3 L/4 截面位置位于两横隔板中间,因此横隔板对其起分担作用较小,相应此截面的腹板承担的剪力较大,故该位置分担比例达80.6%。

表1 各控制截面腹板的剪力分担比例

图4 各控制截面腹板的剪应力分担分布规律
4.2 剪应力偏载系数分析
由于对波形钢腹板施加的剪应力沿腹板高均匀分布,故选取腹板中心点施加的应力大小作为此控制截面腹板剪应力数值。通过有限元分析,分别得出对称活载(工况1)与偏心活载(工况2)的各截面腹板剪应力值,比较2 种工况中各截面腹板的剪应力,即可得出相应截面腹板的剪应力偏载系数。通过选取对称活载与偏心活载作用在箱梁中8 个控制等截面腹板中点的剪力值,并比较分析各控制截面腹板的中载剪应力与偏载剪应力,得出剪应力的偏载增大系数,具体如表2 所示。
由表2 可以看出,当对称活载作用在波形钢腹板预应力组合简支梁腹板时,处于墩顶附近位置的剪应力数值较大;而跨中区域剪力值几乎为0,符合简支梁剪应力的分布规律。根据图5 可知,整个桥梁偏心活载的剪应力增大系数普遍较大,其中大部分截面的剪应力放大系数处于2.6 ~3.4 范围内;跨中位置的剪应力放大系数为最大值,达到4.431,但因跨中位置的截面在对称活载、偏心活载作用下,其附近的剪应力几乎均为0,故剪应力增大系数几乎没有对跨中截面偏载作用造成影响。同混凝土腹板箱梁相比,波形钢腹板预应力组合简支梁桥腹板的剪应力偏载增大系数较大,不宜采用传统剪应力偏载增大系数。
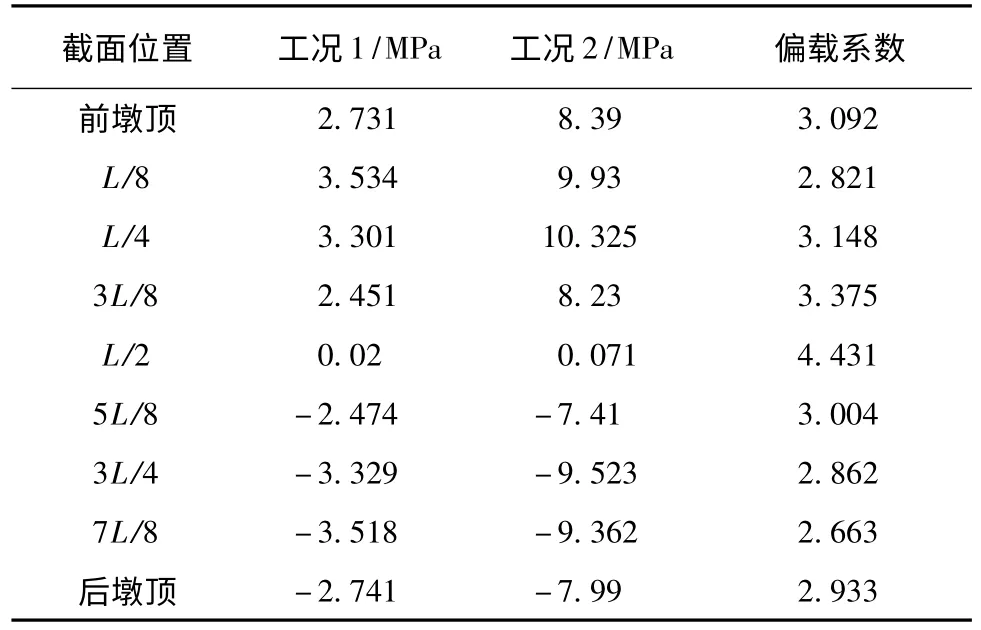
表2 各控制截面腹板中点的剪应力偏载系数

图5 各控制截面腹板的剪应力偏载系数分布规律
5 结论
1)由于箱梁部分截面附近存在内衬混凝土和横隔板,一定程度上增加附近截面的抗剪刚度,相应腹板部分剪力被其分担,致使该截面的剪力分担比例降低。
2)在实际桥梁设计中,活载剪应力的放大系数通常取用1.05,而通过有限元分析得出该波形钢腹板预应力组合简支梁桥各截面腹板的剪应力偏载系数范围为1.22 ~1.42,因此经验估值法不适于波形钢腹板组合梁的偏载系数的计算分析。
[1]孟 磊,刘皓楠,王用中.波形钢腹板PC 箱梁的特点及经济效益分析[J].建筑与工程,2009(13):649-650.
[2]陈宝春,陈宜言,林 松.波形钢腹板桥梁应用调查[J].中外公路,2010,30(2):109-118.
[3]徐 强.波形钢腹板预应力RPC 组合箱梁力学性能研究[D].北京:北京交通大学,2011.
[4]徐 强,万 水.波形钢腹板PC 组合箱梁桥设计与应用(第1版)[M].北京:人民交通出版社,2009.
[5]陈朦朦,万 水.波形钢腹板PC 组合箱梁在我国桥梁工程中的应用[J].湖南交通科技,2006,32(4):124-135.
[6]孙天明,李淑琴.波形钢腹板PC 组合箱梁桥的设计与建造[J].公路,2010(1):79-82.
[7]苏 俭,刘 钊,阮 静.连续梁桥的活载正应力偏载系数研究[J].世界桥梁,2009(4):34-36.
[8]DB41/T696-2010,公路波形钢腹板预应力混凝土箱梁桥设计规范[S].
[9]廖 宇.波形钢腹板PC 组合箱梁桥几个特殊力学性能问题的研究[D].北京:北京交通大学,2011.

