外置阻尼器对基于频率法索力测试的影响

唐钰昇，胡建新，刘大洋

(1.重庆市交通工程质量检测有限公司，重庆 400067;2.招商局重庆交通科研设计院有限公司，重庆 400067)

0 前言

斜拉索作为斜拉桥的主要受力构件，在恒载与活载的作用下，拉索把桥面系的重量与荷载传递给主要承重结构，拉索索力的变化将会影响桥面板以及主要承重结构的受力分配，所以拉索索力是斜拉桥结构的一个重要参数，是斜拉桥工作状态评估的重要依据，拉索的应力状态直接关系到整个桥梁的结构性能和使用安全。

有较多学者研究了拉索的具有弯曲刚度、垂度、面内振动与面外振动的耦合、倾斜、复杂边界条件等对拉索索力测试的影响，如陈常松利用动平衡法推导了考虑弯曲刚度的柔索自振方程和自振频率公式，采用瑞利能量法分析弹性支撑条件和附加质量对拉索自振频率的影响［1］;林智宏等分析了频率法测量索力中索力－频率关系拟合、实测频率的测量、索参数灵敏度分析以及识别等几项关键技术［2］;王朝华等考虑拉索刚度、垂度、边界条件等因素对采用频率法测定索力方面进行了系统分析，均取得良好效果［3］;郑罡等认为多参数识别优于单参数(基频)识别，提高了斜拉索索力测试的准确度和可靠度［4］。王修勇等研究了拉索－阻尼器系统设计对拉索模态频率的影响，认为振动法测量拉索索力时，采取高阶模态频率及计算长度进行评估，可以消除拉索阻尼器对拉索频率的影响［5］。J.A.Main 等人根据美国大量斜拉桥索力的测量经验，总结了各种测量拉索振动的方法，对比了线性与非线性阻尼器抑制拉索振动的效果［6］。日本东京大学Yozo Fujino 教授等引入一般索的模态阻尼比的近似渐近线公式，该公式精确地考虑了拉索的垂度和弯曲刚度，以及阻尼器的有限刚度，公式清晰、简洁，有助于阻尼器的设计应用［7］。

本文主要是考虑外置阻尼器的阻尼系数对拉索振动特性以及对基于频率法索力测试的影响。

大跨度斜拉桥的拉索刚度和阻尼都很小，固有频率和模态阻尼比往往很低，在风、雨等外部环境因素激励下极易发生风振、风雨激振等现象，完全抑制拉索的振动十分困难，为了控制拉索大幅振动，除了在拉索锚固端设置阻尼装置，许多斜拉桥采取在桥面和拉索间安装阻尼器，以增加拉索结构的阻尼。但是外置阻尼器对拉索的自振频率产生了一定的影响，从而影响采用振动法测量索力的精度。研究阻尼器的阻尼系数大小、安装的相对位置对不同长度拉索的自振特性影响，包括低阶与高阶振动自振频率和振型很有必要。本文以某斜拉桥为实例，分析了外置阻尼器对拉索自振频率的影响程度，为振动法测量分析斜拉桥索力和拉索的阻尼器设计提供参考。

1 理论分析方法

1.1 能量法

目前，有部分学者运用能量法来研究外置阻尼器对拉索振动特性的影响。当拉索发生振动时，利用能量守恒定律，拉索的动能与势能在不断的发生着转化，拉索的动能(W)与势能(V)的和不变，即W+V=Wmax=Vmax=常数。能量分析方法是将阻尼器简化为一个具有等效刚度的弹簧，而未考虑阻尼器的阻尼系数，但是工程中应用较广的剪切型粘滞阻尼器的实际刚度很小，拉索振动时主要由阻尼系数发挥作用。如果采用能量法考虑阻尼器的阻尼系数时，能量分析方法会遇到2 个问题，简要分析如下。

当拉索安装外置阻尼器后，拉索的振型函数发生了变化，分为受影响的1/n L 段内，与不受影响的剩余段(n－1)/n L，在能量计算时将进行分段积分，计算简图如图1。

图1 拉索—阻尼器系统振动示意图

图中ε 为外置阻尼器到拉索端部的距离比，图中y(x，t)为不受阻尼器影响段的振动位移函数:

y1(x，t)为受阻尼器影响段的振动位移函数:

上式中ω 为拉索振动角频率;φ 为相位角;a、b为待定常数。

图1 所示振动系统的动能为:

代入振动位移函数积分并整理得:

振动系统的势能为:

代入振动位移函数积分并整理得:

1.2 能量法问题

能量法推导至上面步骤时，发现有2 个问题。

第一，数学上的问题，当W=Wmax时，cos2(ωt+，此时，但是势能V 里面除了有关项外，还多了下面一项:

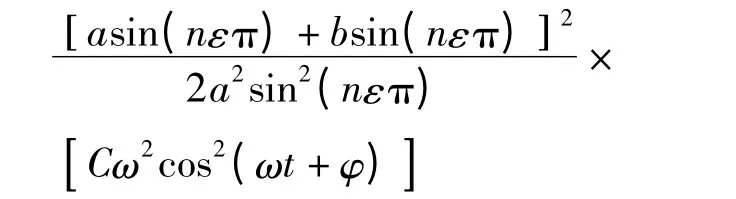
也就是说，当W=Wmax时，V 并不等于0。当系统动能最大的时候，势能并不等于0;或者当系统势能最大的时候，动能并不等于0。这样就与能量法前面的假设W+V=Wmax=Vmax=常数相互矛盾。

第二，这个问题也是运用能量法的关键问题，当考虑拉索阻尼器阻尼系数对拉索的振动影响后，此时就不能用能量法，因为此时的拉索－阻尼器系统是一个非保守系统，里面存着阻尼力这个非保守力做功，阻尼力做功的这部分能量由阻尼器滑板之间的黏性材料的剪切变形所消耗，这时系统的能量不守恒。

所以用能量法可以求解只有等效刚度的阻尼器的拉索振动问题，对于考虑入阻尼器阻尼系数后，不能再用能量法求解，此时的系统变为一个非保守系统。此外，数学上的分析也遇到问题。下面将引入复模态方法来分析拉索外置阻尼器对拉索振动特性的一些影响。

2 复模态方法

首先分析复模态分析方法的基本原理，本文的推导是基于J.A，Main［9］与S.Krenk［10］学者的复模态分析方法进行的。由于剪切型粘滞阻尼器的实际刚度较小，拉索振动时主要由阻尼系数发挥作用。此处只考虑阻尼器的阻尼系数对拉索振动的影响，不考虑拉索的内阻尼、弯曲刚度、垂度对拉索振动的影响，这样简化的结果与张紧弦模型相同，并假设拉索发生面内竖向微幅振动时索力不变，分析简图如图2。

图2 拉索—阻尼器系统振动分析示意图

图中L=l1+l2，l1＜l2，x2=L－x1，拉索上每个微小单元的偏微分方程如下:

上式中yk(xk，t)为拉索面内竖向振动位移;xk表示弦沿轴向坐标的第k 段;T 为拉索索力;m 为单位索长质量。式(7)可以考虑阻尼器安装在拉索的任何位置，并且在阻尼器位置满足力的平衡和位移连续两个条件。这里引入一个无量纲时间τ=ω01t，它表示为在t 时间内发生一阶振动的次数，其中ω01为为安装阻尼器的一阶振动频率，假设式(7)对两部分拉索的解为:

λ 为无量纲的复特征值。将式(7)代入式(8)，得到常微分方程:

由于λ 为复数，上式是一个复微分方程，其解为模态振型，也为复数，阻尼器位置的振动描述可用下式:

γ 为阻尼器位置振幅，阻尼器所在位置力的平衡方程为:

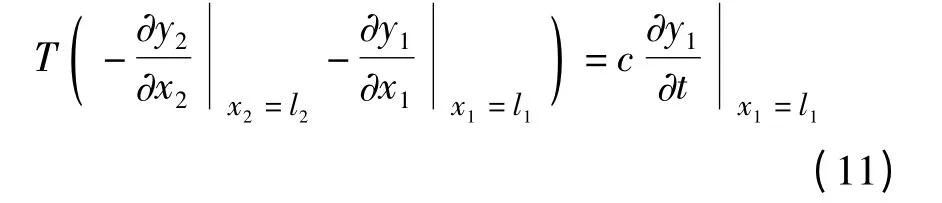
c 为阻尼器阻尼系数，将式(7)式(10)与代入式(11)，得到频率方程:

上式频率方程的根为系统的特征值，分别对应各自的振动模态，每个特征值可以写为:

上式ζi为系统的模态阻尼比;ωi为拉索振动特征值的模。为描述第i 阶特征值的实部和虚部，引入新的符号变量:

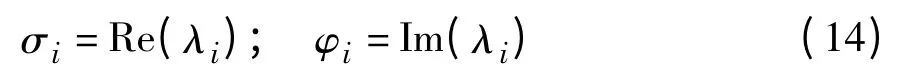
式中φi为无量纲的阻尼振动频率，阻尼比ζi可由σi与φi表示:

对式(12)进一步分解得到:

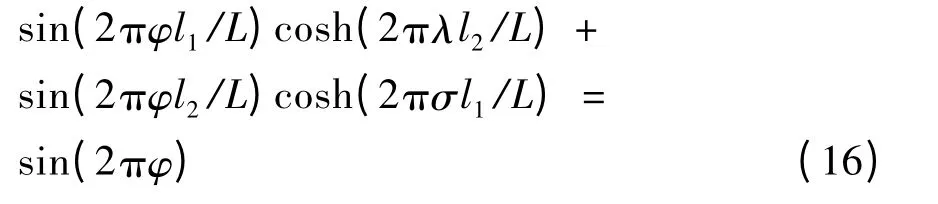
由简化的式(11)实数部分:

在数学上，用解析法对上面复频率方程求解基本是不可能的。下节将采用有限元方法不同拉索的粘性阻尼系数按式(17)进行复特征值分析，可以获得外置阻尼器参数与拉索频率的关系。

3 工程应用

以某斜拉桥主桥选取10 根斜拉索为研究背景，研究阻尼器阻尼系数对拉索振动频率的影响。10根斜拉索分别代表不同长度、索力、外置阻尼器参数的拉索。其中最短拉索为SAY01 拉索，索长55.038 m;最长拉索为NCY25 拉索，索长407.353 m。10 根拉索的基本参数如表1。

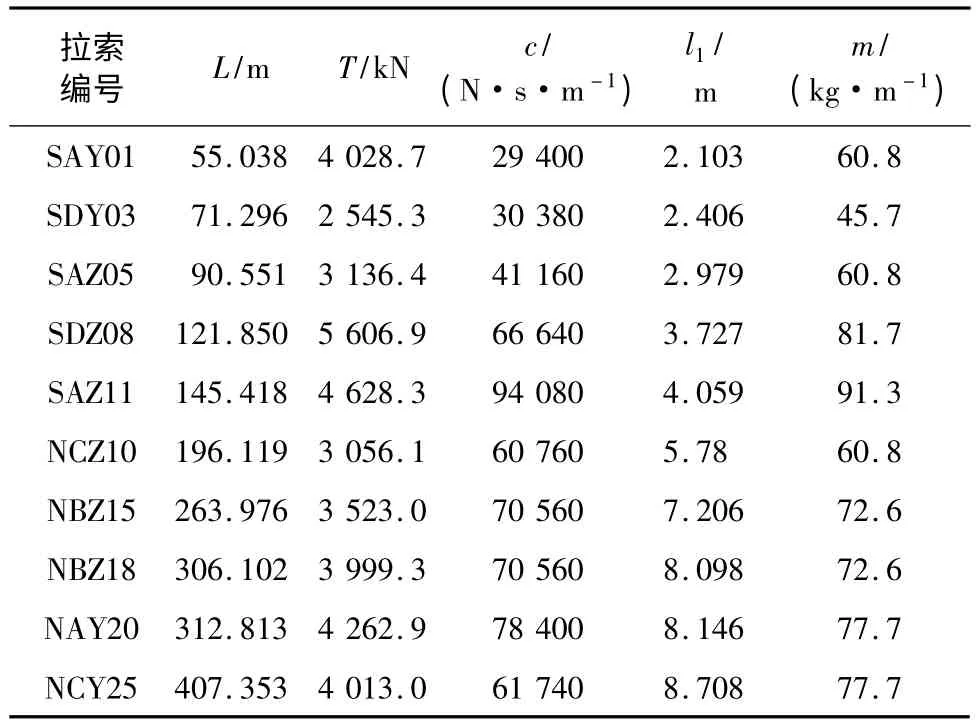
表1 拉索基本参数

表1 中L 为拉索计算长度;T 为索力;c 为阻尼器阻尼系数;l1为阻尼器安装位置与桥面拉索锚固端距离;m 为拉索单位质量。

由于拉索较长，索的刚度和阻尼都很小，固有频率和模态阻尼比很低，加之桥址处风力大，风况复杂，台风季节最大风力达12 级。在风、雨等外部环境因素激励下极易发生风振、风雨激振等现象。为了控制拉索大幅振动，除了在拉索锚固端设置减振装置外，在桥面和拉索间均安装外置阻尼器，以增加拉索结构的阻尼。

采用有限元法对式(17)进行复特征值分析，考虑阻尼器阻尼系数对表1 中10 根拉索自振频率的影响。上述10 根拉索进行分析，对于前4 根较短拉索，由于频差值较大，第30 阶的振动频率45 Hz，此处只分析短索的前30 阶与长索的前45 阶振动频率。以各个拉索的阶次为自变量，以考虑阻尼系数后的拉索自振频率与未考虑阻尼系数的自振频率比为应变量，绘图结果如图3。

由图3 可知:对于长度不等的10 根斜拉索，阻尼系数对拉索自振频率的影响有明显的规律。首先，安装外置阻尼器后，考虑阻尼器的阻尼系数时，拉索的各阶振动频率均提高了，这是由于阻尼器增加了拉索的约束所致。其次，外置阻尼器对拉索振动频率的影响曲线可分为3 个阶段，上升段、平稳段、微下降段。

从量值分析，阻尼器对拉索振动频率的影响均小于5%，最大的影响在最短的SAY01 拉索，频率增幅达到4.71%;最小的影响在最长的SCY25 拉索，频率增幅为2.58%。随着索长的增大，阻尼器对拉索自振频率的影响有减小的趋势。当然这种影响不仅与索长有关，还与阻尼器阻尼系数，以及阻尼器安装在拉索的相对位置有关。

从曲线的3 段性分析，曲线的微下降段的开始点基本位移30 阶或30 阶以上的自振频率，此处不对微下降段做详细分析，主要讨论曲线的上升段与平稳段，因为这两段在实际工程索力测试时可用。由前4 根较短斜拉索的频率影响曲线可见，拉索达到平稳段基本位于20 阶位置，而后面的较长拉索达到平稳段基本位于10 阶位置，也就是说，阻尼器对拉索自振频率的影响，长索先于短索达到曲线平稳段。

通过对影响曲线的分析，对比了外置阻尼器对长短拉索的高低阶频率的影响，利用影响曲线3 段性的特征和数值对比分析得出的相关规律，可以对实际工程斜拉索索力测试提供相关修正参考，以降低索力测试的误差。

图3 不同拉索阻尼系数—频率影响曲线

4 结语

本文首先从能量法入手分析外置阻尼器阻尼系数对拉索振动面内振动的影响，但是遇到数学问题和非保守系统问题。本文再运用复特征值的有限元解法，绘制了阻尼器对长短拉索的高低阶频率的影响曲线，结果表明:

1)针对本文研究的10 根斜拉索，阻尼器对短索的频率影响最大为4.71%，随着索长的增加，影响越来越小，针对长度为407.353 m 的拉索，频率影响最大为2.31%。

2)为减小外置阻尼器对拉索索力测试的影响，可以从两个方面入手。一是采用识别基频或者是二阶频率来换算索力，因为由影响曲线可知，阻尼器对基频、二阶频率的影响较小。二是利用曲线的平稳段，在索力测试时，识别平稳段的拉索振动频率，再根据有限元计算拉索阻尼器影响曲线平稳段的频率增幅，来进行相应的频率修正。

［1］陈常松，陈政清，颜东煌.柔索索力主频阶次误差及支承条件误差［J］.交通运输工程学报，2002，4(4):17－22.

［2］林志宏，徐郁峰.频率法测量斜拉桥索力的关键技术［J］.中外公路，2003，28(5):1－4.

［3］王朝华，李国蔚，何祖发，等.斜拉桥索力测量的影响因素分析［J］.世界桥梁，2004(3):64－67.

［4］郑 罡，倪一清，高赞明，等.斜拉索张力测试和参数评估的理论和应用［J］.土木工程学报，2005，38(3):64－69.

［5］王修勇，谭 艳.斜拉桥拉索减振阻尼器对拉索索力测量的影响研究［J］.振动与冲击，2008，27(11):80－82.

［6］J.A.Main，N.P.Jones.Evaluation of Viscous Dampers for Stay-Cable Vibration Mitigation［J］.Journal of Brideg Engineering，2001，6(6):385－397.

［7］Yozo Fujino，Nam Hoang.Design Formulas for Damping of a Stay Cable with a Damoer［J］.Journal of structural Engineering，2008，134(2):269－278.

［8］Mehrabi，A.B.and Tabatabai，H.Unified finite difference formulation for free vibration of cables［J］.Journal of Structural Engineering，1998，124(11):1313－1322.

［9］.A.Main.N.P.Jone.Free Vibrations of A Taut Cable with Attached Damper 1:Linear Viscous Damper［J］.Journal of Engineering Mechanics ASME，2000，67:68－72.

［10］S.Krenk.Vibrations of A Taut Cable with An External Damper［J］.Journal of Applied Mechanics ASME，2000，67:68－72.