基于裂纹扩展理论的船体结构疲劳评估

牛 松，任慧龙，冯国庆（哈尔滨工程大学 船舶工程学院，哈尔滨 5000；2中国船级社审图中心，上海 20035）

基于裂纹扩展理论的船体结构疲劳评估

牛 松1，2，任慧龙1，冯国庆1
（1哈尔滨工程大学 船舶工程学院，哈尔滨 150001；2中国船级社审图中心，上海 200135）

疲劳破坏是船舶结构的主要破坏形式之一。为了保证船舶结构有足够的疲劳强度，各国船级社、船厂等均建立了船舶结构疲劳强度校核规范作为船舶疲劳评估的指导性文件，尽管这些规范均是建立在S-N曲线方法基础上的，但由于S-N曲线方法存在自身无法克服的缺陷（如忽略材料的初始缺陷等），对同一节点进行计算得到的疲劳寿命大相径庭。该文作者在基于裂纹扩展理论的基础之上，给出了一套详细的船体结构疲劳评估方法，并应用此方法对大型船舶结构典型节点的疲劳寿命进行评估，以期能为完善船舶结构疲劳寿命的评估提供参考。

船舶结构；疲劳评估；裂纹扩展理论；应力强度因子

0 引 言

疲劳破坏是船舶结构的主要破坏模式，也是船舶力学领域的研究热点。目前，实用的船舶结构疲劳评估主要采用S-N曲线法[1-2]，各船级社给出的船舶结构疲劳评估方法也是采用这种方法。但是由于这种方法建立在光滑试件试验基础上，没有考虑材料缺陷（如表面划痕、金属夹杂、腐蚀坑、锻造缺陷等）造成各种类型裂纹对构件疲劳寿命的影响。而含有这种裂纹的构件在交变载荷作用下，即使载荷低于材料本身的疲劳强度极限，裂纹也会很快扩展而断裂，导致灾难性的破坏。崔维成、祁恩荣、黄小平[3]认为，船舶结构疲劳计算在理论上的缺陷使得要想在线性累积损伤方法的框架下提高疲劳寿命预报方法的精确度是非常困难的，因为许多试验已经证明了材料初始缺陷和载荷裂纹次序对疲劳寿命有重要影响。而基于断裂力学的疲劳评估方法由于该方法本身的不足以及断裂力学及相关数学力学理论及计算技术的发展，使得以裂纹疲劳扩展为基础的疲劳寿命预测方法成为目前研究疲劳问题的热点。越来越多的人已经认识到，下一代的船舶结构疲劳强度校核方法必须是基于裂纹扩展理论或断裂力学的新方法[4-5]。鉴于此，本文在裂纹扩展理论的基础上对船舶结构疲劳寿命评估方法进行了研究，并以半椭圆表面裂纹为例，给出了一套基于裂纹扩展理论的船体结构疲劳评估实用预报方法。

1 基于裂纹扩展理论的船体结构疲劳评估方法

1.1 应力强度因子的求解及修正

应力强度因子是裂纹扩展的主要驱动力，求解应力强度因子的方法有解析法、权函数法、切片合成法和边界元法等。本文采用权函数法计算应力强度因子。

权函数法[6]给出了解耦裂纹几何和载荷配置两类影响的途径，其物理意义可解释为在裂纹结构的裂纹面上x处作用成对的单位力（在上下两表面分别作用相等的单位压应力）所产生的应力强度因子（如图1所示），它只与裂纹体几何（包括应力边界和位移边界的划分方式）有关，一旦从某一载荷中导出，则可用来计算任意载荷条件下的应力强度因子K（边界力和体力的积分）：

式中：σ（t）

x即为无裂纹体假想裂纹处的应力分布。

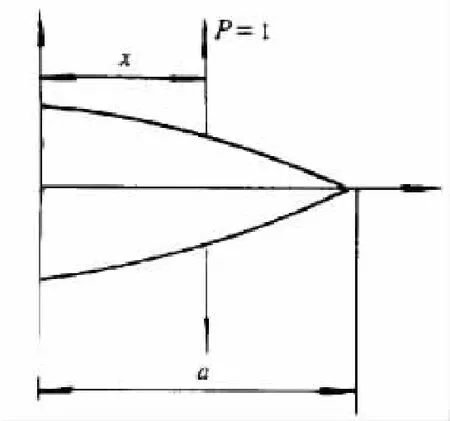
图1 单位力引起的应力强度因子（权函数）Fig.1 Stress Intensity Factor induced by unit force (Weight function)

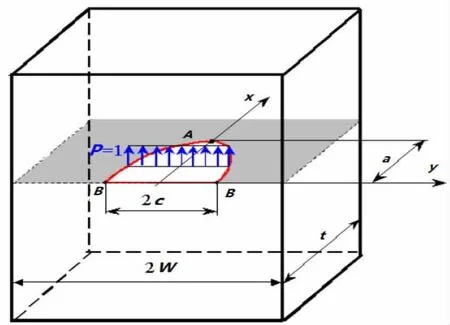
图2 有限板宽内的半椭圆表面裂纹模型Fig.2 Semi-elliptical surface crack in a finite thickness plate

作为裂纹体的权函数，（m x,a） 只与裂纹结构有关且对给定的裂纹结构是唯一的，与所加的外载无关。因此，对于某种裂纹体，一旦它的权函数确定，则该裂纹体的应力强度因子可以由一系列无裂纹时垂直作用在裂纹面上的应力所产生的应力强度因子叠加得到。对于半椭圆表面裂纹（如图2所示），有：

半椭圆表面裂纹最深点A处：

半椭圆表面裂纹表面点B处：

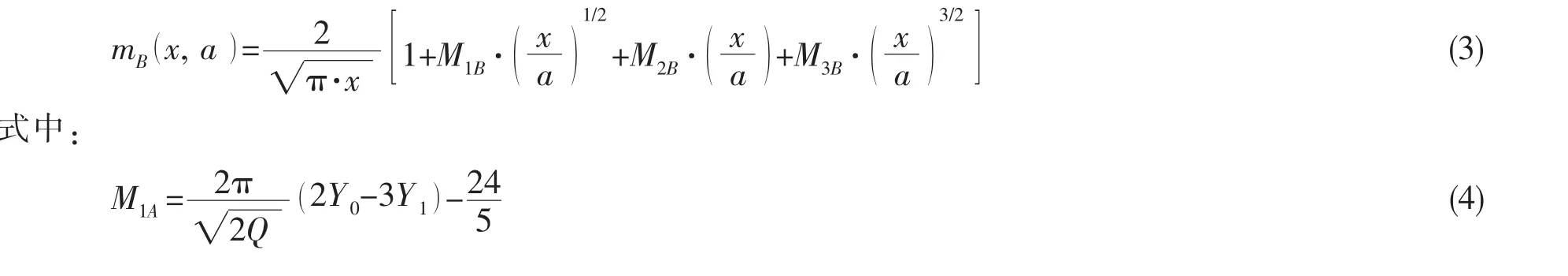
根据参考文献[7]，有：

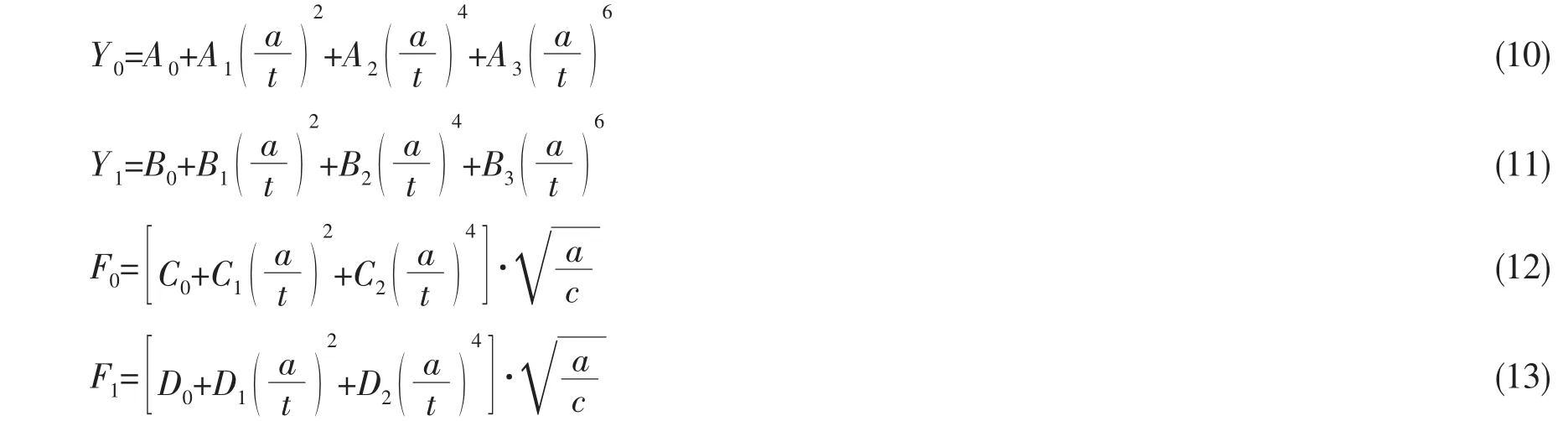
式中：参数A0，A1，A2，A3，B0，B1，B2，B3，C0，C1，C2、D0，D1及D2的表达式涉及系数众多，篇幅所限，在此不一一列出[7]。

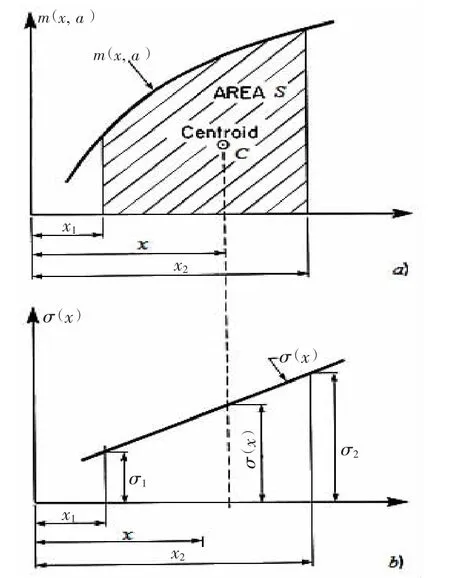
图3 简单节点形式对应的权函数与应力函数Fig.3 Weight function and stress distribution for simple structural configuration

图4 复杂节点形式对应的权函数与应力函数Fig.4 Weight function and stress distribution for complicated structural configuration

与权函数m（x, a）对应的应力分布函数σ（x）则可从无裂纹的有限元模型中提取后拟合得到，它与裂纹的形式和所在的位置有关，其求解不涉及裂纹问题。对于简单形式的节点，其权函数和应力分布函数分别单调线性且仅随x的变化而变化（图3），应力强度因子可表示为权函数曲线下所对应的面积与应力函数的乘积形式：

对于结构形式复杂的节点，其受力也相对复杂，拟合出的应力函数分布很可能是非线性的，同时，其所对应的权函数可能也是非线性的（图4），我们可以将积分区间（即裂纹扩展区域）分为n个子区间，这样应力函数在每个子区间内可以近似认为是线性分布，有：

式中：Ai

代入（1）式，有：

又由（14）式，有：

式中：Si为相应权函数m曲线下的面积；Xi为对应的坐标。

显然，权函数在积分区间内是光滑连续的。在每一个子区间内，裂纹参数可近似认为是不变的，则根据裂纹的形式和具体参数可以得到m。我们根据图4可以定义：

考虑到焊接加工时产生的残余应力σR对疲劳性能的影响，一般有两种处理方式：一种是平均应力观点，即把残余应力作为平均应力处理，通过Goodman关系来估算残余应力对疲劳性能的影响；另一种观点则是基于断裂力学的观点，即认为残余压应力的存在降低了构件的应力强度因子ΔK，通过有效应力强度因子幅ΔKeff来估算残余应力对裂纹扩展速率da/dN的影响，从而估算构件的疲劳寿命。

本方法认为残余应力σR是沿焊缝方向和垂直于焊缝方向的应力，大小为σR=0.3σs，然后将σR叠加到外载作用的应力上，以此计算应力强度因子K。此外，还应考虑由焊趾处应力集中所引起的焊趾应力强度因子放大系数MK，修正后的应力强度因子可表示为：

式中：MK根据新版英国规范BS7910选取[8]。

1.2 裂纹体疲劳寿命的预报

本文采用Paris提出的裂纹扩展速率公式：

由Paris公式知，对它们在a0→ac区间内求定积分即可得到疲劳裂纹的扩展寿命N：

式中：N0为裂纹扩展到a0时的循环次数（若a0为初始裂纹长度，则N0=0）；NC为裂纹扩展到临界失稳断裂长度ac时的循环次数；C和m为材料常数，一般通过实验获得。由于本方法主要针对船用钢，故取C=1.83E-13，m=2.736[9-12]。

裂纹扩展会导致裂纹体的有效承载面积减小，从而使得板或骨材所承受的应力增加，一旦该应力超过材料本身的屈服限时可认为裂纹体失效破坏,此时的裂纹长度即为上式中的ac[13]。显然，在载荷一定的情况下，应力强度因子随裂纹长度的增加亦呈递增趋势变化。本文将裂纹从a0→ac的整个扩展过程分为若干个小份da，并认为裂纹在a0→a0+da区间扩展时应力强度因子为一定值K1，代入（23）式可求得在a0→a0+da区间的疲劳裂纹循环次数N1，然后同理可求得K1、K2、K3……Ki……KC，依次对应可求得N1、N2、N3……Ni……NC，最后将每个应力强度因子所对应的循环次数逐项累加，即可得到在整个a0→ac区间内的总循环次数N：

2 实船算例

本文以某79 000 DWT为目标船，采用基于裂纹扩展准则的断裂力学方法，对其舯部货舱区域顶边舱舷侧板与横框架相交处、内底板与实肋板相交处、顶边舱及底边舱舷侧纵骨位置四处部位（图5.1）进行疲劳寿命评估。

2.1 有限元模型化

图5.1 裂纹所在位置处的有限元细化模型Fig.5.1 The fine mesh FE model in way of the crack

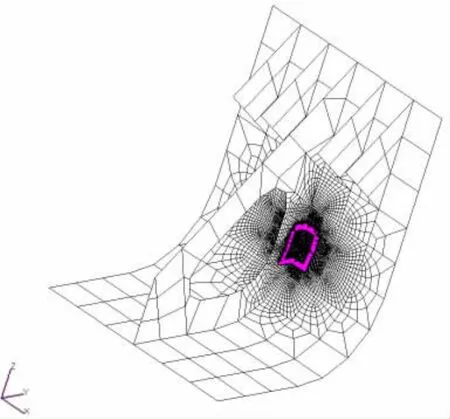
图5.2 底边舱舷侧纵骨处裂纹细化模型Fig.5.2 The fine mesh FE model of crack in way of longitudinal stiffener on side shell within hopper tank

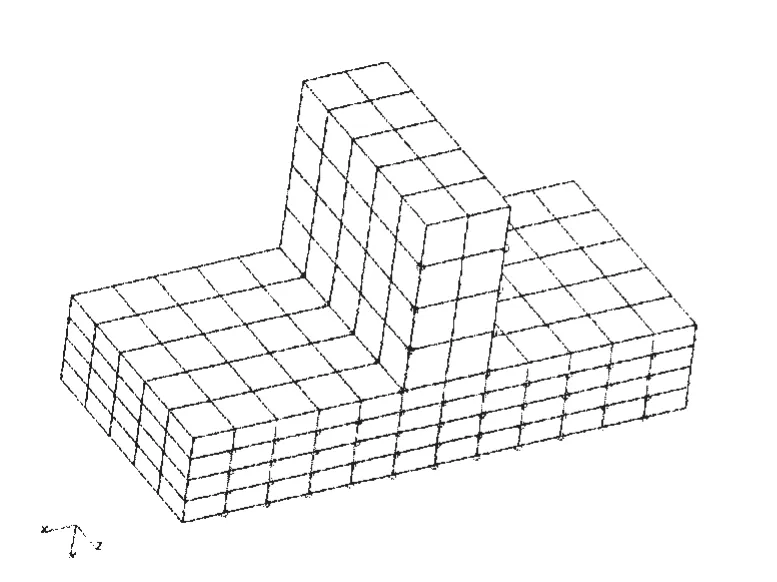
图5.3 三维模型细化区域（体单元）Fig.5.3 The range of fine mesh in the 3-D model with solid elements

图5.4 裂纹处体单元与板单元的连接方式Fig.5.4 The transition between solid element and shell element in way of crack

由1.1节可知，在利用权函数方法确定裂纹的应力强度因子时，与裂纹垂直方向的应力分量可通过无裂纹的有限元模型来模拟得到。由于船体结构表面裂纹多沿厚度方向扩展，为了更真实地模拟实际结构，得到裂纹在厚度方向较真实的应力分布，作者在对校核区域进行节点细化的基础上，还应用三维实体单元来模拟实际结构，且与周围的板单元用MPC（多点约束）连接[14-15]，以期得到垂直裂纹面方向的更为精确的应力分布（图5.2-5.4）。

2.2 载荷的确定和施加

本文以均值为零的恒幅交变载荷作用下裂纹扩展为例，即在舱段模型两端利用MPC施加波浪弯矩，提取在幅值（波峰波谷）时刻垂直于裂纹面的拉应力。对于压应力，由于对裂纹扩展没有贡献，故不计入疲劳寿命的计算。图6所示为舱段模型加载示意图。

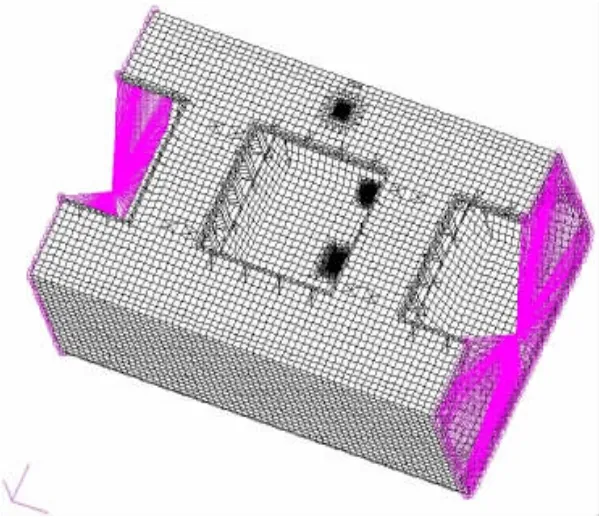
图6 舱段模型加载示意图Fig.6 The loads and pressures applying on global model

2.3 计算结果

在有限元模型中提取与裂纹有公共边的板或体单元所受与裂纹表面相垂直的应力并沿裂纹扩展方向拟合出应力函数曲线，再根据权函数公式求得应力强度因子K，修正后通过前面1.2中的方法求得总循环次数N。

2.3.1 顶边舱舷侧板与强框架相交处

裂纹所在位置处受与裂纹表面相垂直的应力函数曲线如图7所示。

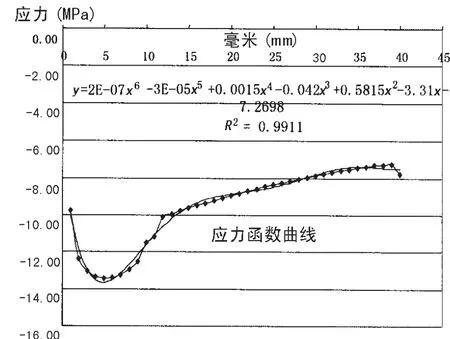
图7 顶边舱舷侧板与强框架相交处应力函数曲线Fig.7 Curve of Stress distribution in way of connection between side shell and upper wing tank web

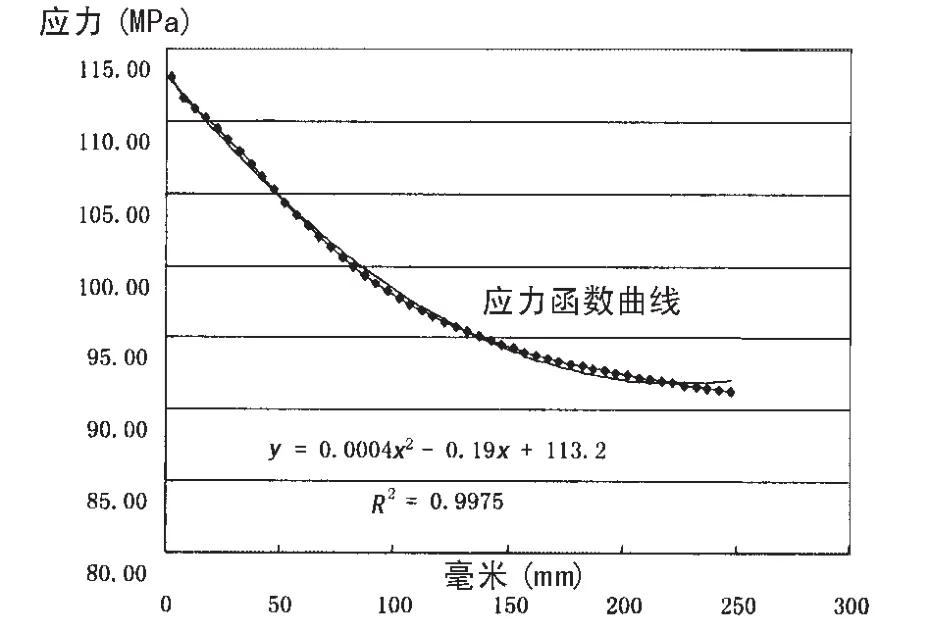
图8 内底板与实肋板相交处应力函数曲线Fig.8 Curve of Stress distribution in way of connection between inner bottom and bottom floor

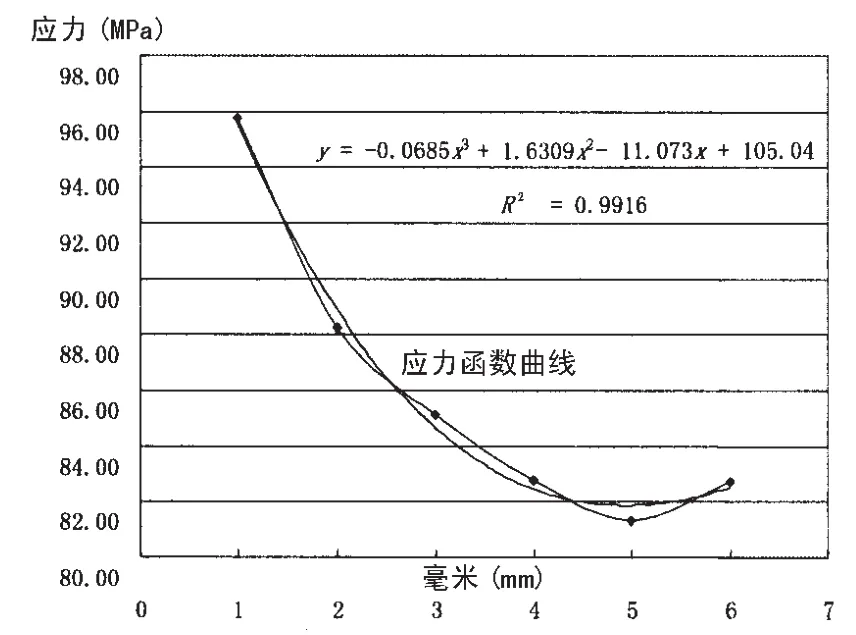
图9 底边舱舷侧纵骨位置处应力函数曲线Fig.9 Curve of Stress distribution in way of longitudinal stiffener on side shell within hopper tank

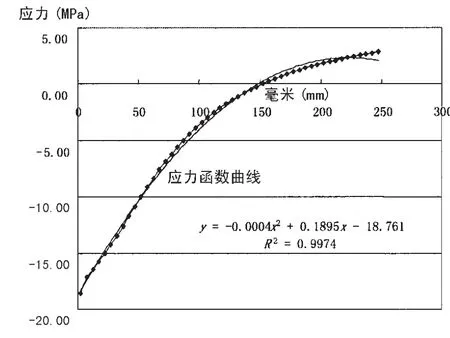
图10 顶边舱舷侧纵骨位置处应力函数曲线Fig.10 Curve of Stress distribution in way of longitudinal stiffener on side shell within upper wing tank

2.3.2 内底板与实肋板相交处

裂纹所在位置处受与裂纹表面相垂直的应力函数曲线如图8所示。

2.3.3 底边舱舷侧纵骨位置处

裂纹所在位置处受与裂纹表面相垂直的应力函数曲线如图9所示。

2.3.4 顶边舱舷侧纵骨位置处

裂纹所在位置处受与裂纹表面相垂直的应力函数曲线如图10所示。

3 校核节点处疲劳寿命比较

作者所选取船体结构的几处典型节点在基于裂纹扩展理论和S-N曲线（采用热点应力方法，选取E曲线计算）两种不同方法下进行疲劳寿命校核的结果详见表1。

表1 两种方法下校核所得循环次数比较Tab.1 A comparison of the cycle index obtained from the two methods

对于所选取目标船舯部货舱区域四处典型目标节点分别采用基于裂纹扩展理论和S-N曲线（E曲线）两种不同方法下进行疲劳寿命校核所得的结果表明：基于裂纹扩展理论和基于S-N曲线（E曲线）的方法所求得相同位置处的循环次数基本在同一个量级，但前者所得的结果明显要偏大一些，从这点上说明现行规范所使用的S-N曲线方法进行船体结构的疲劳寿命评估显得较为保守。

S-N曲线的应用对象是光滑无裂纹的理想构件，该构件从无裂纹到有裂纹需要时间较长，但一旦出现裂纹很快便破坏了，它没有把疲劳裂纹的发生与扩展区别开来，也没有揭示出疲劳裂纹扩展的各个阶段。而实际船体结构多为存在有初始裂纹的大型复杂结构，对于这些大型结构，裂纹的扩展在整个疲劳寿命中占有支配地位（约占整个疲劳寿命的90%，远大于疲劳寿命的萌生阶段）。基于裂纹扩展理论的疲劳评估方法以权函数法为基础，用无裂纹的三维有限元模型来模拟实际的有裂纹结构，首先确定裂纹的初始长度a0，再选择合理的断裂判据用以确定裂纹的临界尺寸ac，并在具体计算中充分考虑焊接工艺上通过渗碳渗氮等方法来给构件表面层（约0.08-0.40 mm）引入残余压应力所降低的构件疲劳裂纹扩展率、所选材料参数的准确性（C，m等，通常由实验测得）以及部分焊趾处的应力集中影响等因素，尽可能真实地模拟出实际裂纹体的疲劳寿命，从而更好地服务于老龄船评估、钢板换新等工程应用。

4 结 论

本文给出了一套基于裂纹扩展理论的船体结构疲劳评估方法，针对某79 000 DWT散货船建立有限元模型，并选取四处典型节点位置用细化的三维体单元来模拟裂纹，然后用基于裂纹扩展理论的断裂力学方法对这些典型节点的疲劳寿命进行校核。由于缺少具体的实验数据作为参照，只能和传统的S-N曲线（E曲线）方法的校核结果在理论层面进行分析阐述，并拟综合考虑裂纹的闭合效应、过载效应以及疲劳载荷的随机性等方面进一步加以完善，以期能为下一代基于裂纹扩展理论的船体结构疲劳强度校核新方法的确定提供参考。

参考文献：

[1]IACS.Common structural rules for bulk carriers[S].January,2006.

[2]中国船级社.船体结构疲劳强度指南[K].中国船级社,2007 China Classification Society.Hull structure fatigue strength guide[K].CCS,2007.

[3]崔维成,祁恩荣,黄小平.船舶结构强度预报/评估方法的现状和未来发展趋势[C]//2005年船舶结构力学学术会议论文集.中国造船工程学会,中国舟山,2005. Cui Weicheng,Qi Enrong,Huang Xiaoping.Strength of ship structure forecast/evaluation methods of present situation and future development trend[C]//Ship Structural Mechanics in 2005 Academic Conference Proceedings.CSNAME,Zhoushan, China,2005.

[4]Cui Weicheng.A feasible study of fatigue life prediction for marine structures based on crack propagation analysis[J].Journal of Engineering for the Marine Environment,2003,217(5):11-23.

[5]Rapid Stress Intensity Factor Solution Estimation for Ship Structures Application[Z].PB2004-101320.2004.

[6]Bueckner H F.A novel principle for the computation of stress intensity factor[J].ZAMM,1970,50:529-546.

[7]库默,等著[美].周洪范,等译.弹塑性断裂分析工程方法（EPRI报告NP-1931）[M].北京:国防工业出版社,1985.

[8]BS7910.Guide on methods for assessing the acceptability of flaws in structures[K].British Standards Institution,1999.

[9]赵章焰,等.Q235钢裂纹扩展参数的实验测定[J].武汉理工大学学报,2003. Zhao Zhangyan,et al.Test on the parameters for the crack propagation of steel Q235[J].Journal of Wuhan University of Technology,2003.

[10]程 靳,赵树山.断裂力学[M].北京:科学出版社,2006.

[11]钢结构设计规范.GB50017[S].2003. GB50017-2003,Rules on the design of steel structures[S].2003.

[12]朱嘉第,方向威,等.机械工程材料数据性能手册[M].北京:机械工业出版社,1995.

[13]沈成康.断裂力学[M].上海:同济大学出版社,1996.

[14]詹志鹄,吴晓源,崔维成,吴龙周.折角型船体结构细节有限元细化分析的程序化方法[J].中国造船,2008(1):51-57. Zhan Zhihu,Wu Xiaoyuan,Cui Weicheng,Wu Longzhou.Programming method of the hull knuckling structure detail refine finite element analysis[J].China Shipbuilding,2008(1):51-57.

[15]IACS HPT08 Form1-harmonization of fatigue strength for IACS CSR rules[S].

Fatigue strength assessment of ship structures based on the crack propagation theory

NIU Song1,2,REN Hui-long1,FENG Guo-qing1
(1 College of Shipbuilding Engineering,Harbin Engineering University,Harbin 150001,China; 2 China Classification Society Plan Approval Centre,Shanghai 200135,China)

Fatigue damage is one of main forms of ship structures destroyed.Every classification society and shipyard take fatigue assessment rules of ship structures as an instruction to assure fatigue strength of ship structures.Although these rules are based on the method of S-N curve,different fatigue lives of the same node are obtained with the help of different rules,because the disadvantages of S-N curve could not be avoided,such as neglect of initial objection of material.In this paper,fatigue strength assessment methods of ship structures are studied based on the facture propagation theory,and a detailed fatigue assessment method of ship structures is proposed,which is supposed to reference to predict fatigue life and preparation to perfect fatigue strength assessment of ship structures.

ship structures;fatigue assessment;crack propagation theory;stress intensity factor

U661.4

A

10.3969/j.issn.1007-7294.2015.08.010

1007-7294（2015）08-0958-08

2014-12-19

牛 松（1982-），男，硕士研究生，工程师，E-mail:niusong1982@ccs.org.cn；任慧龙（1965-），男，教授，博士生导师。