泡状流中空化与激波相互作用的数值模拟

董洪辉，王宝寿，陈玮琪，张珂

（中国船舶科学研究中心，江苏无锡214082）

泡状流中空化与激波相互作用的数值模拟

董洪辉，王宝寿，陈玮琪，张珂

（中国船舶科学研究中心，江苏无锡214082）

文章针对定常可压缩泡状流中回转体的空化绕流进行了数值模拟，在给定来流速度和环境压力的条件下，对不同含气率下的空化与激波的相互作用进行了研究。首先，对含气率为0的情形进行计算并同试验数据进行对比，证明所采用的计算模型是可信的。其次，改变流场含气率从0至0.5进行计算，结果表明，随着含气率的增大，流场的可压缩性随之增强，体现为数值模拟得到了回转体绕流流场的3种波系，包括回转体头部处的脱体激波、分离面处的膨胀波和空泡尾端的斜激波。而空化与激波的相互作用则体现为：头激波削弱了空化效应，使得空化区域减小；由于空泡外形的影响，使得空泡尾端出现了斜激波；含气率超过一定值，空泡已经无法闭合在物面上，而是闭合在空泡尾端的激波面上，体现为空泡尾端壁面逆压梯度趋于平缓。计算结果揭示了泡状流中空化与激波相互作用的新的物理现象。

泡状流；激波；空化

0 引言

均匀混合的气液两相流具有可压缩性，Karplus等人[1]的试验研究表明，当偏离单相极点时，气液混合物的声速迅速降低，特别是当气相体积分数为0.5时，气液两相流的声速接近最小，只有几十米每秒，如图1为不同压力下声速与含气率的关系。因此，在等温条件下，泡状流中就可以产生激波，此类激波称为动力激波。

Eddington[3]对气液两相流中的超音速现象进行了研究，得到并证实了当气相体积分数为0.5时泡状流中的正激波基本关系。Jhon等人[4]在等温条件下，忽略相间速度滑移，提出了一种势流线性分析方法，对在泡状流中高速移动的扰动点所产生激波的波型进行了研究。Saito等人[2]使用单相流模型通过求解可压缩N-S方程组，对NACA0015水翼的三维非定常云空化绕流进行了数值模拟。陈红兵[5]使用速度入口条件计算了水翼在气相体积分数为0.5的来流中的跨声速流动，在超声速来流条件下得到了水翼前端的弓形脱体激波，虽然计算中使用了空化模型但是没有观察到空化现象。

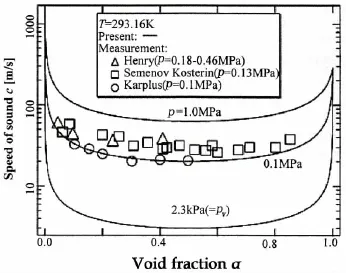
图1 声速与含气率的关系[2]Fig.1 Relation between the speed of sound and the void fraction[2]

可见，对泡状流动的可压缩性的理论和数值研究，多集中于气相体积分数为0.5的情形，尚没有对不同含气率情况下泡状流中空化现象开展研究，因而也没有对空化与激波的相互影响进行研究。本文基于CFD并在给定来流速度的条件下，对回转体在不同气相体积分数下的泡状绕流场中空化与激波的相互作用进行了数值模拟。

1 多相流基本控制方程

本文采用商用软件Fluent 12中Mixture多相流模型进行数值模拟，忽略相间速度滑移[4]，其主要控制方程为[6]：

混合物连续性方程

混合物动量方程

其中：μt为湍动粘度，混合物粘度

混合物能量方程

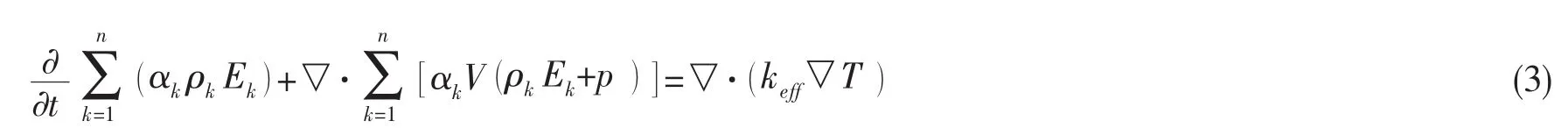
气相体积分数方程

理想气体状态方程

标准k-ε湍流模型

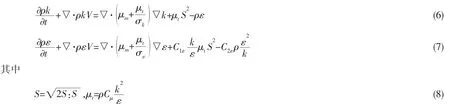
其中：常数取值为C1ε=1.44，C2ε=1.92，Cμ=0.09，σk=1.0，σε=1.3。

Zwart-Gerber-Belamri空化模型的汽相输运方程

其中：Re和Rc分别表示蒸汽泡生成和溃灭的质量源项：

其中：蒸汽泡半径RB=10-6m，气核体积分数αnuc=5×10-4，汽化系数Fvap=50，凝结系数Fvap=0.001。

2 计算网格、求解器设置及验证

2.1 计算网格与求解器设置

研究对象为回转体，其头部接近圆锥，后体为半径R=100 mm、长度L=1 000 mm的圆柱，不计及尾部影响，将圆柱尾端延伸至流场出口边界。由于流动具有对称性，因此计算域为二维轴对称网格，其中入口边界距回转体头部50R，圆柱长度L=100R，出口边界距回转体头部100R，如图2。使用ICEM CFD 12.0进行结构化网格划分，共划分71 631个四边形单元，回转体附近网格采用C型网格，如图2所示。

图2 计算域与回转体附近网格Fig.2 Computational domain and mesh around the body

陈红兵[5]的数值试验表明，当泡状流中气相本身为低亚声速流动或气相马赫数小于0.1时，速度入口条件可用于泡状流的无穷远或入口边界条件。因此，入口和外部边界均采用速度入口条件，给定来流速度为V∞＝30 m/s；回转体表面采用壁面无滑移无穿透条件；出口采用压力出口条件；计算域的中轴线设置为轴对称边界条件；流场初始温度T=300K，工作压力P=138 540 Pa，空化数σ=0.3。

采用基于压力—速度耦合的SIMPLE算法进行求解，计算过程是非定常的，采用Mixture多相流模型，忽略各相间的速度滑移，第一相为水，第二相分别为空气和水蒸气，其中空气为理想气体。以圆柱直径为特征长度的雷诺数Re=3×106，采用标准k-ε湍流模型，近壁处理采用标准壁面函数。边界湍流参数设置同褚学森等人[7]所采用的一致，为Turbulent Intensity=0.5%，Turbulent Viscosity Ratio=5。

空化模型采用Zwart-Gerber-Belamri模型，饱和蒸气压为3 540 Pa。

2.2 计算模型验证

来流速度V∞＝30 m/s、工作压力P=138 540 Pa（即空化数σ=0.3），对含气率αg=0的情形进行了计算，并同权晓波等人[8]的试验结果进行了对比，如图3所示。

由图3的回转体绕流流场的密度云图可以清晰地看见空泡外形以及尾部的回射流结构，而壁面压力系数曲线与试验结果吻合得较好，这表明所采用的计算模型是可信的。

图3 回转体密度云图和壁面压力系数曲线Fig.3 Axis-symmetrical body’s density color contour and pressure coefficient curve on wall

3 计算结果及讨论

基于以上经过验证的计算模型，本文保持来流速度V∞＝30 m/s、工作压力P=138 540 Pa，计算了气液均匀混合介质含气率0～0.5的流动状况，以期得到含气率导致的可压缩性对回转体绕流流场的影响。

3.1 含气率对绕流流场的影响

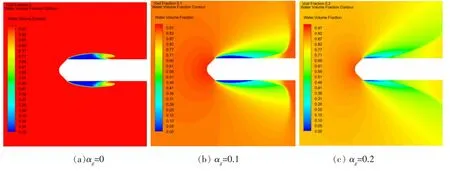
图4至图6分别给出了各含气率下的水相体积分数云图、绝对压力云图和各含气率下的来流马赫数和无量纲空泡长度。由图4可见，不同含气率下，水相在流场中的体积分布差异很大。而造成这种差异的原因正是含气率导致的流场可压缩性的不同：从图5可以看到回转体绕流流场的压力分布，由于流场含气，气相在压力高的区域受压缩，在压力低的区域膨胀，从而导致回转体头部驻点附近的高压区水相体积分数最高，而分离面后的低压区水相体积分数最低；含气率的升高也导致了流场可压缩性的增强，由图6可见，来流速度不变的情况下，随着含气率的增大，来流马赫数逐渐增大，当含气率增至0.3附近，来流马赫数开始大于1，故在图4（e）、（f）和图5（e）、（f）中可以清晰地看到回转体头部前端存在脱体激波。

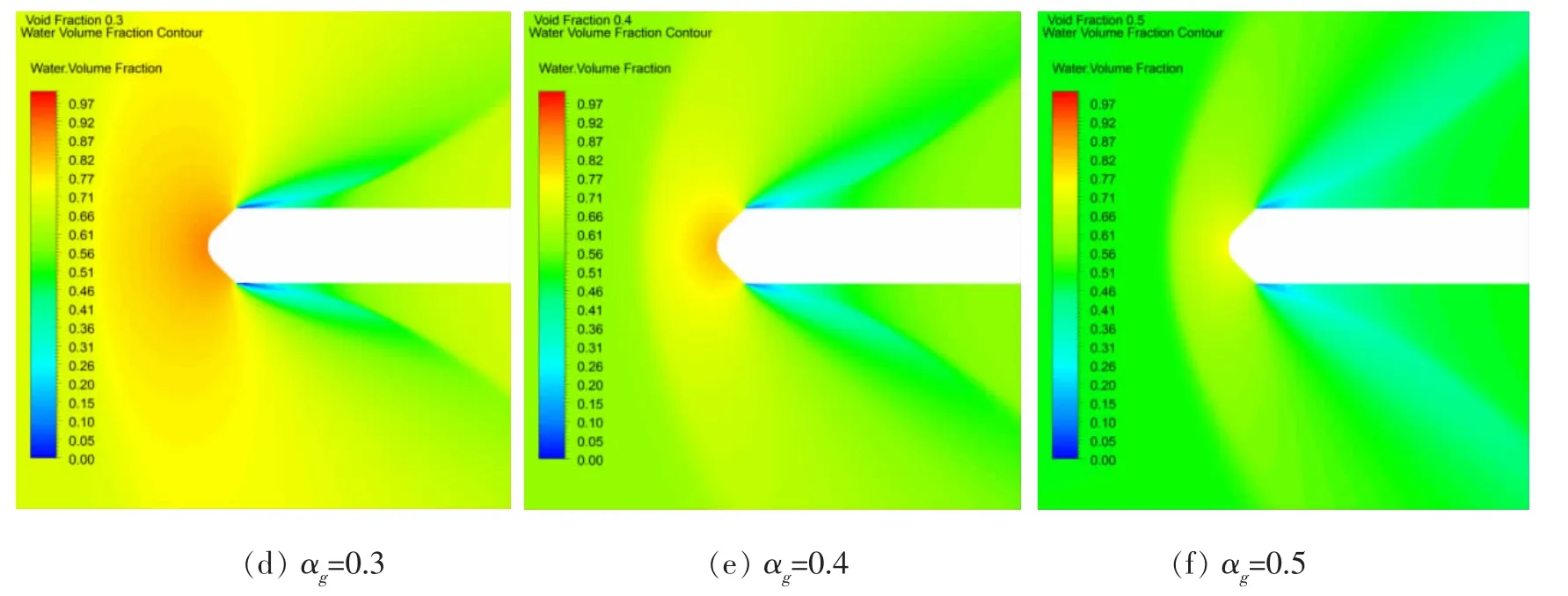
图4 各含气率下水相体积分数云图Fig.4 Water volume color contours of each gas fraction

图5 各含气率下绝对压力云图Fig.5 Absolute pressure color contours of each gas fraction

图4给出的是水相体积分数云图，分离面后水相体积分数低的区域即是空泡，若将空泡界面定义为ρ=0.9ρm，则图6给出了不同含气率下无量纲空泡长度。由图6可见，随着含气率的增大，空泡长度先增大后减小，其原因可以由空泡的气体成分来解释：空泡内气体由水蒸汽和空气两部分组成，随着含气率的增大，由图5可见回转体分离面后的低压区逐渐减小，则空化效应被减弱，因而空泡内的水蒸汽部分逐渐变少；但是流场中均匀混合的空气对空泡可起到通气作用，随着含气率的增大其作用愈发明显；含气率较低时，通气作用对空泡长度的增益占优，含气率较高时，空化效应减弱对空泡长度的影响占优，两种因素综合影响下，导致了空泡长度先增大后减小。

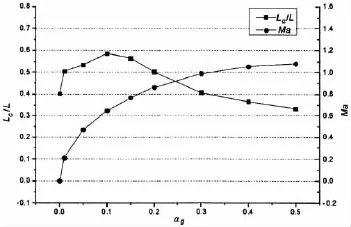
图6 不同含气率下来流马赫数和空泡无量纲长度Fig.6 Incoming flow Mach number and dimensionless cavitylength of each gas fraction

3.2 空化与激波的相互作用

上一节中，我们已经知道随着含气率的升高，流场可压缩性增强，流场中将出现激波。现在，让我们来研究当流场可压缩性增强至出现激波时，激波与空化的相互作用。

图7 各含气率下Ma数云图Fig.7 Mach number color contours of each gas fraction

图7给出了各含气率下的Ma数云图，从中可以对比流场的可压缩性（其中为了便于进行对比，云图标尺是相同的）。图7（a）表明，含气率为0时，流场基本是不可压缩的；图7（a）至（f）表明，随着含气率的增大，来流马赫数逐渐增大，当αg=0.5时，可以清楚地看到回转体头部出现脱体激波，这说明随着含气率的升高，来流流场的可压缩性逐渐增强；由图7（b）-（f），可以看到头部分离面处都出现了膨胀波，而空泡尾部出现了激波，这也从另一个侧面说明气液掺混的混合介质具有了可压缩性。对比图7（b）和（f），发现含气率为0.1时的Mamax比含气率为0.5时要大，这是由于空化效应和含气率的相互作用导致的：如图1所示，气液混合物的声速是压力和含气率的函数，压力越低、含气率越接近于0.5，声速越低；当含气率为0.1时，回转体头部还未出现头激波，分离面后的空化效应比较明显，该处压力仅为水的饱和蒸汽压量级并且局部含气率接近0.5；当含气率为0.5时，回转体头部存在头激波，波后压力较高；因此，含气率为0.1时流场中的Mamax比含气率为0.5时要大。另外，由图7（b）也验证了气液混合物的声速与含气率的关系—在回转体头部驻点处水相占支配地位，而在回转体分离面后空化区域蒸气相占支配地位，因而两处的Ma数均较小；而在空泡界面附近，各相掺混导致局部含气率接近0.5，故Ma数最大。

由前面的分析知，回转体绕流流场可能存在头部脱体激波、分离面处的膨胀波和空泡尾部的压缩波，图8给出了典型情况下回转体空泡绕流流场的波系示意图，其中空泡界面定义为αl=0.1。下面对回转体泡状绕流流场的波系产生的原因进行分析。

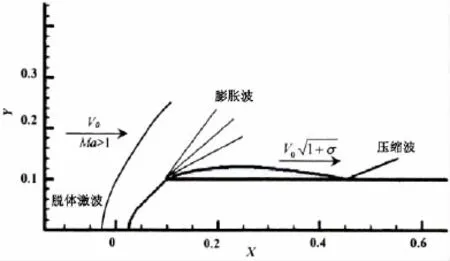
图8 回转体空泡绕流流场的波系Fig.8 Wave system of flow field around axis-symmetrical body

图9为含气率αg分别为0～0.5时的压力等值线图。对比可以发现，当含气率增大至一定程度时（由图6，αg≈0.3时，来流Ma≥1），在回转体头部会出现脱体激波，而产生脱体激波后，波后压力升高，这也是图6中当αg＞0.1后空化长度减小的原因之一；对比有无含气的情形可以发现，由于含气率导致的流场大范围的可压缩性，使得空泡尾端无法闭合在物面上，而是闭合在激波面上，如图9（b）-（f）所示。

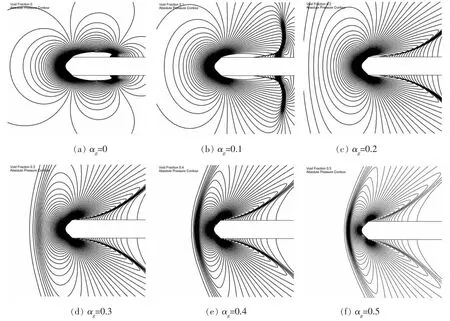
图9 各含气率下压力等值线图Fig.9 Absolute pressure contour line of each gas fraction

图10为αg=0.1时蒸气相体积分数云图和Ma数云图，其中图10（b）为便于显示Ma≥1的区域，云图标尺下限定为Ma=1。可以发现，虽然含气率αg=0.1时，来流Ma数小于1，但是由于在蒸汽泡界面附近，空隙率接近0.5，由图1可知，则空泡界面处马赫数大于1为超声速流，故如图10（b）所示在流经凸钝角时产生了扇形膨胀波；空泡界面附近的流场膨胀加速后依旧为超声速流，而由于空泡外形的影响，空泡尾端相当于形成了凹钝角，超声速流动流经该处形成了斜激波。此外，由于绕流流场的压力分布和含气率分布不均匀，导致各地声速的分布也不均匀，最终导致的结果就是空泡尾端的激波面为曲面，如图10（b）所示。

图10 αg=0.1时蒸气相体积分数云图和Ma数云图Fig.10 Vapor volume color contour and Mach number color contour of gas fraction 0.1

3.3 不同含气率对空化水动力的影响

为研究不同含气率对回转体绕流流场空化水动力的影响，对含气率αg=0～0.5工况的壁面压力系数进行了对比，如图11所示，其中压力系数的定义为

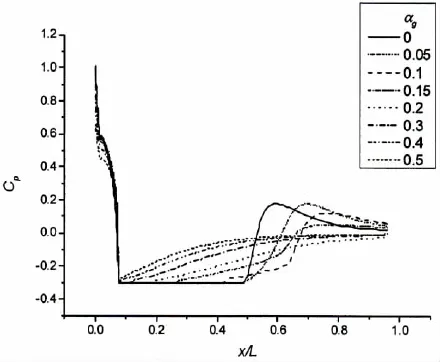
图11 各含气率下壁面压力系数曲线Fig.11 Pressure coefficient curve on wall of each gas fraction

图11表明，随着含气率的增大，压力系数最小的区域（即可能产生空化的区域）逐渐变短，其原因为随着含气率增大，混合介质的可压缩性增强（特别是头部脱体激波的产生），导致分离面后的低压也随之升高，从而导致低压力的空化区域减小。因此，随着含气率的增大，流场的空化效应被削弱。另外，由图11也可以看出，随着流场含气率的增大，空泡尾端的逆压梯度逐渐减小；当含气率αg≥0.2时，逆压梯度已变得相当平缓；这印证了前面的结论，由于流场含气带来的大范围可压缩性的影响，空泡已经无法闭合在物面上，而是闭合在空泡尾端的激波面上，从而体现为空泡尾端壁面逆压梯度减小。

4 结论

本文对回转体的可压缩泡状绕流进行了数值计算，其中含气率αg=0的计算结果与试验结果进行了对比，验证了本文计算模型的合理性。各含气率下的计算结果表明，随着含气率的增大，流场的可压缩性也相应增强，体现为数值模拟得到了回转体绕流流场的3种波系，包括回转体头部处的脱体激波、分离面处的膨胀波和空泡尾端的斜激波。而空化与激波的相互作用则体现为：头激波削弱了空化效应，使得空化区域减小；由于空泡外形的影响，使得空泡尾端出现了斜激波；当含气率超过一定值时，空泡已经无法闭合在物面上，而是闭合在空泡尾端的激波面上，体现为空泡尾端壁面逆压梯度趋于平缓。本文的计算结果揭示了可压缩泡状流动的新的物理现象，有助于实验结果的验证。

[1]Karplus H B.The velocity of sound in a liquid containing gas bubbles[J].Armour Research Foundation of Illinois Institute of Technology,1958:C00-248.

[2]Saito Yoshinori,Takami Rieko,Nakamori Ichiro,Ikohagi Toshiaki.Numerical analysis of unsteady behavior of cloud cavitation around a NACA0015 foil[J].Computational Mechanics,2007,40(1):85-96.

[3]Eddington.Investigation of supersonic shock phenomena in a two-phase(liquid-gas)tunnel[J].AIAA,1970,08(01):65-74.

[4]Grant J R,Kirschner I N.High-speed motion in bubbly flows[C]//Fifth International Symposium on Cavitation(CAV2003). Osaka,Japan,2003:1-10.

[5]陈红兵.定常可压缩泡状流动激波的数值仿真[J].船舶力学,2012,12(10):1107-1114. Chen Hongbing.Numerical study on the shocks in thesteady compressible bubbly flows[J].Journal of Ship Mechanics, 2012,12(10):1107-1114.

[6]ANSYS Inc.ANSYS FLUENT 12.0 Theory Guide[K].2009.

[7]褚学森,王志,颜开.自然空化流动数值模拟中参数取值影响的研究[J].船舶力学,2007,11(1):32-39. Chu Xuesen,Wang Zhi,Yan Kai.Parametric study on numerical simulation of natural cavitation flow[J].Journal of Ship Mechanics,2007,11(1):32-39.

[8]权晓波,李岩,魏海鹏,王宝寿,孔德才.大攻角下轴对称航行体空化流动特性试验研究[J].水动力学研究与进展A辑,2008,23(6):662-667. Quan Xiaobo,Li Yan,Wei Haipeng,Wang Baoshou,Kong Decai.An experiment study on cavitation of underwater vehicle’s surface at large angles of attack[J].Journal of Hydrodynamics,Ser.A,2008,23(6):662-667.

Numerical simulation on interaction between cavitation and shock wave in compressible bubbly flows

DONG Hong-hui,WANG Bao-shou,CHEN Wei-qi,ZHANG Ke
(China Ship Scientific Research Center,Wuxi 214082,China)

The numerical simulation on the cavitating flow around an axis-symmetrical body in the steady compressible bubbly flow was simulated,and the interaction between cavitation and shock wave under different air volume fractions with the constant flow velocity and operating pressure was investigated.Firstly,to verify the used calculation model,the case which air volume fraction takes 0 in the incoming flow was calculated and shows a good agreement with the experimental result.Secondly,more cases with air volume fractions varying from 0 to 0.5 were calculated.The results show that with the increase of air volume fractions, flow field becomes more compressible.This result was confirmed by the appearance of three kinds of wave systems,including detached shock wave before the head,expansion wave at separation surface and oblique shock wave after cavity tail.The interaction between cavitation and shock wave is reflected as follows:bow shock before caviting region weakens cavitation effects,making caviting region decrease;cavity generated by cavitation results in occurrence of oblique shock;cavity closure point cannot locate on the body surface but on the shock surface,which can be confirmed by the adverse pressure gradient at the end of cavity.These results revealed a new physical phenomenon which existed in the interaction process between the cavity and the shock wave in compressible bubbly flows.

bubbly flow;shock wave;cavitation

U661.3

A

10.3969/j.issn.1007-7294.2015.11.001

1007-7294（2015）11-1295-09

2015-08-15

董洪辉（1989-），男，硕士研究生，E-mail：donghonghui@163.com；

王宝寿（1963-），男，研究员。