有限元分析在数控机床热误差检测中的应用* ＊

库祥臣 苗庆地 郭跃飞 段明德

(河南科技大学机电工程学院，河南 洛阳471003)

机床误差主要包括几何误差、热误差和切削力误差，其中热误差占总误差的40% ～70%左右，并且对于越精密的机床，热误差所占比重越大［1］。目前几何误差已经得到了很好的解决，从而使得热误差成为了提高机床加工精度的主要研究对象。热误差补偿技术是减小热误差的多种方法中经济且易于实现的一种，并且在各种实验中已经成功实现。例如Debra. A.Krulewich 利用高斯积分法建立了热误差补偿模型，成功减少了93% ～96%的主轴热误差［2］;Chih －Hao Lo等人通过建立优化模型将主轴热误差从20.0 μm 减小到2.2 μm［3］;浙江大学以CK616 －1 数控车床为研究对象，成功实现应用改进型BP 神经网络对热误差建模分析［4］。传感器优化布置是热误差补偿技术实现的一大障碍，现今主要根据经验或是多传感器优化来实现传感器的有效布置。此次应用ANASYA14.0软件建立了数控机床主轴箱装配体的有限元模型，采用热—结构耦合分析方法完成了热瞬态分析和结构静态分析［5］，从中得出了主轴箱温度场和热变形云图，进而确定传感器安装位置。

1 前期计算

1.1 搭建平台

以型号为CK6142 的数控机床主轴箱装配体为对象，主轴转速500 r/min、1 500 r/min 进行仿真，初始温度26℃。装配体各部件材料为:主轴箱HT200、主轴45#钢、轴承GCr15，并由此可得出计算所需的材料属性:密度kg/m3、弹性模量N/m2、泊松比、热导率W/(m·K)、比热容J/(kg·K)、热膨胀系数。

1.2 轴承发热量计算

轴承发热为主轴箱装配体的主要热源，精确计算发热量是建模成功的关键。滚动轴承发热量Q计算公式:

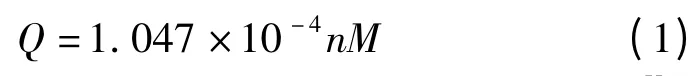
式中:n为轴承转速，r/min;M为摩擦力矩，N·mm［6］。摩擦力矩M=M0+M1，速度项M0是无负荷轴承的摩擦力矩，反映了润滑剂的流体动力损耗;负荷项M1则反映了滚动摩擦效应，尤其是滞后和滑动摩擦效应。

速度项M0，根据Palmgren 提出的算法:

式中:f0为考虑轴承结构类型和润滑方式的经验常数;v为所选润滑剂的运动粘度，mm2/s;dm为轴承中径，mm。

负荷项M1为:

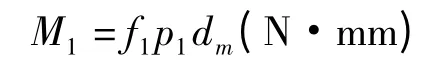
式中:f1为与负荷及轴承结构类型有关的摩擦系数，可由轴承的额定静载荷和当量静载荷求出;C0为额定静载荷，P0和P1分别为当量静载荷、当量动载荷。

1.3 边界条件计算

分析采用了热—结构顺序耦合分析，在后者分析中位移约束为边界条件，可将装配体安装固定面作为边界。热分析边界条件主要有热传导、热对流和热辐射。导热系数可以在材料属性中确定，考虑到辐射散热量较小，文中主要进行对流系数的计算。

(1)轴承与压缩空气对流换热系数 因在每次润滑油喷射中油量较小，可以忽略油气所吸收的热量，只考虑轴承与压缩空气的对流换热。对流换热系数是主轴转速与空气流量的函数:α =9.7 +5.33μ0.8。轴承内外圈空气平均流速为:

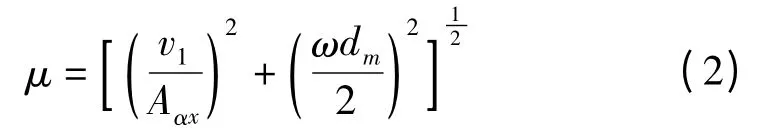
式中:v1为轴承内外圈空气流量，m3/s;Aαx为轴向气流流动面积，m2，Aαx=2πdmΔh;Δh为轴承内外圈与保持架的间隙，m;ω 为主轴旋转角速度，rad/s;dm为轴承中径，m。根据轴承内径和润滑方式确定了空气流量，从而计算出前后轴承在500 r/min 时的对流换热系数为339.74 W/(m2·℃)，323. 9 W/(m2·℃)，在1500 r/min 时的对流换热系数为346.04 W/(m2·℃)，324.14 W/(m2·℃)。

(2)主轴和主轴箱与空气的对流换热系数 主轴箱内的空气因轴和齿轮的旋转而产生流动，属于强制对流;主轴箱外壁空气由于壁温升高而流动，为自然对流。根据Nusselt 准则，强迫对流系数为:α =(λ/l)·Nu，其中λ 为空气导热率;l为特征尺寸，对于平板类其为板长，对于轴类其为直径;Nu根据对象不同分为外掠平板类Num和横掠单管类Nuf。

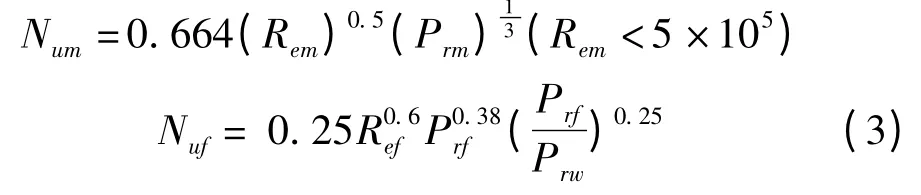
式中:Ref和Rem为雷诺数;Prm为依据来流温度和壁温平均值确定的普朗特数;Prf和Prw为依据来流温度和壁温分别确定的普朗特数，且因与空气对流，可不考虑修正项［7］。

箱体内主轴部分的对流系数经计算得20.4 W/(m2·℃)，根据经验，作为边界条件其为理论计算值的3 ～10 倍，经多次试验与实际温度对比，取数值80 W/(m2·℃);主轴箱外壁的自然对流系数可选5 W/(m2·℃)。

毕业生是指在学校学习期满，达到规定的要求，准予毕业的学生。在计划经济市场下，毕业生直接分配到企业就业，没有机会进行自主选择。现如今的就业环境下，毕业生在取得毕业证和学位证后，可以结合自己的兴趣、性格、价值观和所学专业知识，进行自我推销，从而进入心仪的企业工作，可以将自己的所学真正应用到生产实践中，降低了跳槽的几率，增加了毕业生自我效能感和成就感。

2 施加边界条件的有限元素模型

建立有限元模型时，对CK6142 机床主轴箱装配体进行了简化，略去影响较小的轴肩、键等结构，应用了SOLID70 和SOLID97 单元进行网格划分，最终产生62691 个节点。图1 为施加温度边界条件后的有限元素模型。将生热率施加到主轴前后轴承处，处于主轴箱体内外部分的主轴表面施加各自的强制对流系数，主轴箱箱体内表面施加强制对流系数，外表面则为自然对流系数。

3 热—结构耦合分析及结果说明

3.1 瞬态热分析

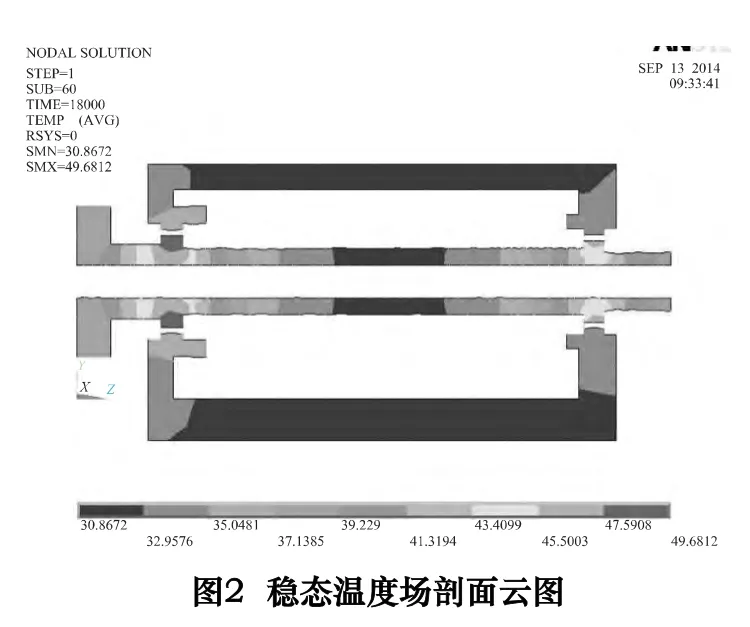
瞬态热分析最终状态即为稳态温度场分布，因考虑到在不同转速下装配体高温区域分布相似且在转速1 500 r/min 下的稳态温度场温度层次更分明，故只列出了1 500 r/min 的温度剖面云图如图2 所示。由图可知，主轴箱装配体高温区域为前后轴承处，且轴承内圈温度高于外圈，这与主轴重心距离端部较近有关，主轴前轴承内圈温度最高，达到49.68 ℃，最低温度为30.87 ℃;而在500 r/min 下的最高、低温度则为27.6℃、26.2 ℃。高温区域主要集中在轴承周围，这使得装配体受热不均，易于产生弯曲变形。

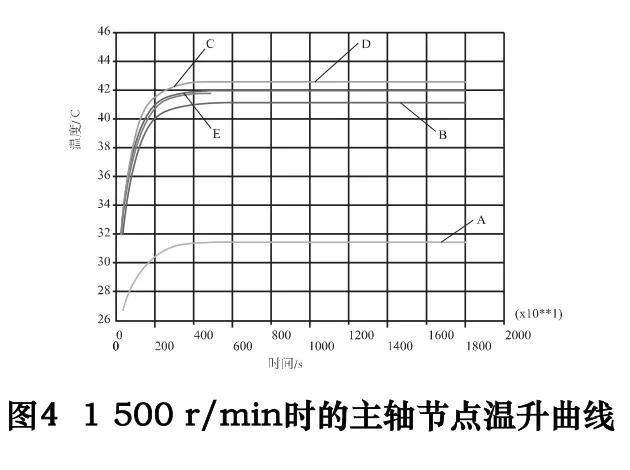
取主轴端部点A，距前后轴承相同距离的点B、C、D、E，画温升曲线，如图3、4 为500 r/min、1 500 r/min转速下的温升曲线。

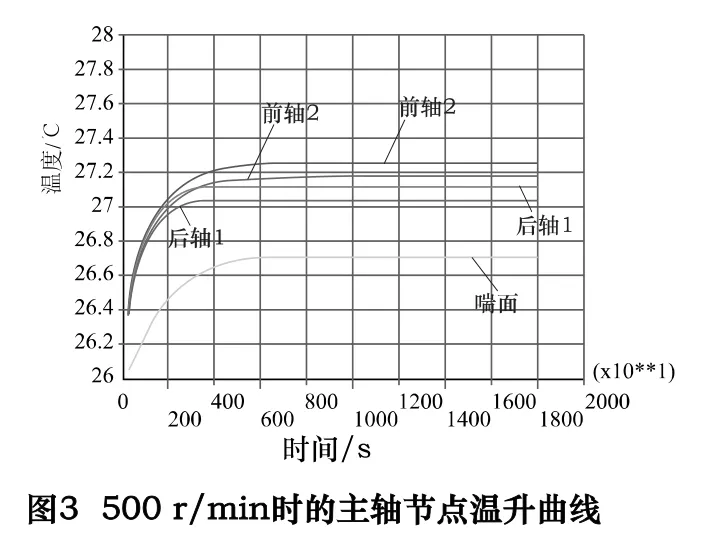
由图可知，在500 r/min、1 500 r/min 下，主轴各点热平衡时间约为10 000 s、6 000 s，曲率大的温升时间为6 000 s、4 000 s。在热误差测温点选择中，应优先选择热敏感区域，主轴前后轴承温升曲线相关性较大，端部轴承温差变化大，可将端部轴承区域设为测温度点以减小传感器数量。由于结构、材料的原因，主轴箱温度平衡时间较长，其温升曲线与主轴温升曲线的相关性较小。主轴箱热源为轴承外圈，在结构分析中可以较为直观地得出其与热误差的关系。

3.2 应变分析

有限元分析采用热—结构顺序耦合方式，最终得出装配体的热应变。在500r/min 时装配体最大变形量不超过2 μm，而在1 500 r/min 时的最大变形量则达到48 μm。

(1)主轴轴心偏移 主轴箱装配体因受热膨胀，使得主轴轴心在空间位置上发生了偏移。1 500 r/min时主轴箱在前后轴承处的径向位移分别为12. 497 μm、11.3 μm，应用热倾角公式α = arctan(ΔR/ΔL)(ΔR为径向变形量之差，ΔL为两径向截面距离)［8］，计算得1.3581 ×10－4°;500 r/min 时前后轴承处径向位移为0.028 77 μm、0.001 01 μm，热倾角为(2.3216×10－6)°。由此可得，热误差与主轴箱热变形有着直接关系，箱体热敏感区域为测温必需位置。由于转速低时变形量太小，不仅对传感器要求较高，而且易于受其他误差影响，因此，热误差测量时高转速是一必备条件。

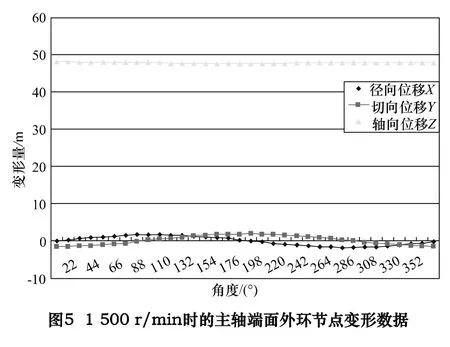
(2)主轴热变形 主轴除了受热产生热变形外，还受到轴承内圈的挤压。1 500 r/min 时主轴在前后轴承处的径向位移1.894 μm、0.443 72 μm，计算热倾角为(6. 6454 × 10－4)°。观察主轴应变云图，主轴变形程度在头部端面最明显，图5 为端面边缘各节点的三向位移和综合位移。由图可知，端面处各点轴向位移远大于其他方向位移，且数据波动小。对于平面测位移传感器，主轴端面可以测得较为精准的位移。

(3)主轴头部跳动误差 在1 500 r/min 时，从仿真分析结果得到主轴头部跳动误差，主轴在径向、切向的跳动误差为1.743 μm、1.894 μm，考虑到节点间未计算数据，这两个跳动误差是极其相近的。而实际生产中，机床因受热膨胀，主轴和主轴箱发生形变，从而导致主轴轴心在多方向上发生偏移，这使得径向和切向跳动误差相差较大，数据变化更加复杂。

4 结语

通过对主轴箱装配体进行热—结构耦合分析，得到相应的温度和位移云图，根据装配体各部件的热敏感区域，确定测温区域。对于非接触式温度传感器，可以以主轴和箱体为测温对象;而接触式传感器，则以主轴箱为测温对象。观察不同转速下主轴和箱体节点温升曲线，得到了热平衡时间和温度随转速的变化规律，为热误差数据采集时间指定了范围。装配体位移云图显示了主轴、轴承和主轴箱相互作用后的变形，根据相互接触区域节点的位移数据，得出了主轴在空间位置的挪移和自身热膨胀引起的端面位移，指出了位移传感器的安装位置，为进一步优化测点位置奠定了基础。

［1］赵海涛. 数控机床热误差模态分析、测点布置及建模研究［D］. 上海:上海交通大学，2007.

［2］Krulewic D A. Temperature integration model and measurement selection for thermally induced machine tool errors［J］. Mechatronics，1998(8):393 －412.

［3］Lo C H，Yuan Jingxia. Optimal temperature variable selection by grouping approach for thermal error modeling and compensation［J］. International Joural of Machine Tool＆Manufacture，1999(39):1383 －1396.

［4］傅龙珠，狄瑞坤，项国锋. BP 神经网络补偿热变形误差的研究［J］.机床电器，2002，8(3):11 －15.

［5］凌桂龙，李战芬. ANASYS14.0 从入门到精通［M］. 北京:清华大学出版社，2013:342 －344.

［6］埃斯曼，哈市巴根，韦根特，等. 滚动轴承设计与应用手册［M］. 武汉:华中工学院出版社，1985:145 －151.

［7］《机械工程师手册》第二版编辑委员会. 机械工程师手册［M］.2版.北京:机械工业出版社，2000:1039 －1065.

［8］张耀满，刘启伟. 数控车床主轴部件及其主轴箱热特性有限元分析［J］.东北大学学报，2011，32(4):571 －574.