基于Akhras-Dhatt算法的区域剖分法

王如云，于音弦，臧振涛，曹 迪，陈 林

(1.河海大学港口海岸与近海工程学院，江苏 南京210098;2.河海大学 力学与材料学院，江苏南京210098)

把地球流体、固体等大型科学计算问题的计算域划分成较小的子区域，并映射到各计算节点，是并行计算中的一个重要过程，称为区域剖分。寻求各计算节点上负载平衡的计算网格优化划分方法，称为区域剖分法(Domain Decomposition Method)，其结果将直接影响着并行计算的并行效率。因此，区域剖分法一直是国内外许多高性能计算科研工作者的研究重点之一。

由于能够对复杂外形进行准确、有效地拟合，无结构网格在有限单元法、有限差分法、有限体积法等数值方法中都有广泛应用。目前，基于无结构网格进行并行计算时，常用的区域剖分方法有:阵面推进法(Advancing Front Technique)［1-2］、图划分法(Graph Partitioning Methods)［3］等，其中图划分法又包含递归谱对剖分法(Recursive Spectral Bisection，RSB)［4-6］、 多 层 次 算 法 (Multilevel Algorithms)［7-8］、Multilevel Recursive Spectral Bisection(MRSB)方法［9］、超图剖分法(Hypergraph Partitioning)［9-10］等。

阵面推进法的优势在于其操作简单，且易于实现，但其存在计算量大、实施过程较复杂等问题;递归谱对剖分法具有分割量近似最小，使得处理器间信息交换量接近最小的优点，但由于该算法所形成的Lagrangian矩阵大小，与总的单元数量成平方关系，这就消耗了大量内存，同时该算法需要求解Fiedler特征向量也需要大量的计算时间;多层次算法大致可分为粗化、分区与优化3个阶段，优化阶段一般采用 Kernighan-Lin/Fiduccia-Mattheyses(KL/FM)［11］类方法，但该算法实现步骤比较复杂，KL/FM的使用会加大整体耗时量;MRSB方法结合了多层次算法与RSB方法，是目前国际上比较通用的方法，该方法具有处理器的开销较小、计算速度较快等优点，但由于有限元模型的几何拓扑信息在粗化过程中会出现部分丢失现象，造成各个分区的元素不均衡和边界过长等不良结果;超图剖分方法能够非常精确地表示通信量、具有外部通信量较小等优点，但它存在费用开销大于其它图剖分方法的缺点。

根据计算节点个数情况，把所有单元按编号顺序，均匀分配到各个计算节点是一种较为简单易于实现的区域剖分方案。但是直接对由自动网格剖分程序生成的单元，按单元编号进行区域剖分其并行效率一般很低。通过研究分析，文中给出单元邻接矩阵带宽与外部通信量间的关系，发现通过减小带宽可以达到减少外部通信量，提高并行效率的目的。减小矩阵带宽可以通过给网格单元进行编号优化来实现，其方法较多。如Akhras和DhattG于1976年提出一种通过优化网格节点编号来减小高阶稀疏矩阵带宽的算法［12-13］，简称AD(Akhras和Dhatt G)算法就是其中一种。AD算法简便且利于并行处理。

基于AD算法思想，文中提出一种区域剖分方法。首先利用AD算法给无结构网格优化编号以减少邻接矩阵的带宽，然后根据优化后的单元编号顺序和单元属性，将计算单元均匀地映射到各个计算节点上。通过算例与其它剖分方法比较，结果表明该方法能够实现各处理器上负载的更为优化的平衡，对处理大型数据具有可行性和有效性。

1 单元邻接矩阵带宽与并行计算效率间的关系

在通常的流体、固体等数值模拟计算中，当前单元物理量的计算需要调用其周边单元的数据。当将网格进行区域剖分后，会造成部分需要数据传输的单元不在同一计算节点上，这就需要进行节点间的外部通信。适当减少外部通信量，可以提高并行计算效率。

为研究方便，将整个计算域的网格单元进行编号:1，2，…，N。先给出如下 3 个定义:

1)相关单元:在当前单元上进行数值计算时，需要调用到其它单元上的有关数据，这些被调用数据的单元称为当前单元的相关单元。若第i个单元是第j个单元的相关单元，就一般的计算格式而言，第j个单元也是第i个单元的相关单元，称单元i和单元j相关。

引进

一般数值计算时会调用当前单元上的数据，因此取aii=1。若记，则该值与单元的具体编号无关，是邻接矩阵的一个不变特征量。

2)单元邻接矩阵:矩阵A=(aij)N×N称为单元邻接矩阵，满足A=AT。

3)按单元序号区域剖分法(简称序号法):假设计算节点总数为r，现把N(N=Kr)个单元上的计算任务按单元编号顺序，均匀分配到各个计算节点，其中第I(I=1，2，…，r)个计算节点承担单元编号(I－1)K+1，…，IK总共K个单元的计算任务。

在进行按单元编号顺序区域剖分法后，此时单元邻接矩阵分解成r阶分块矩阵

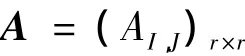
其中

AI，J=(a(I－1)K+i，(J－1)K+j)K×K，I，J=1，2，…，r显然，第I个计算节点与第J个计算节点间需要交换信息的单元总数 EI，J，就是分块矩阵 AI，J中的元素和，即

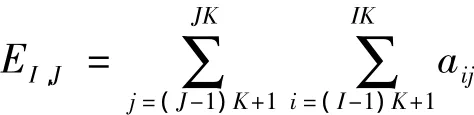
第I个计算节点与第J个计算节点间有关通信量与 EI，J成正比，比例系数为常数。当 I=J 时，EI，J表示第I个计算节点内部通信的单元总数;当I≠J时，EI，J表示第I个计算节点与第J个计算节点间外部通信的单元总数。因此，第I个计算节点与其它所有计算节点(J=1，…，I－ 1，I+1，…，r)间的外部通信的单元总数为

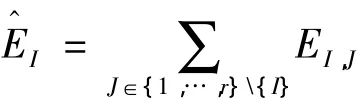
假设邻接矩阵的半带宽为L(见图1)，则位于带状区域外的元素，即当|i－j|＞L时有ai，j=0;而在位于带状区域内的元素，即当|i－j|≤L时ai，j取值可能等于1。假设带状区域内，除主对角线上元素取值为1外，其它位置的元素取值为1的机会相等，利用特征量m0可导出外部通信的单元总数

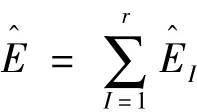
的计算公式，分两种情况进行研究。

1)当K≤L+1≤N时

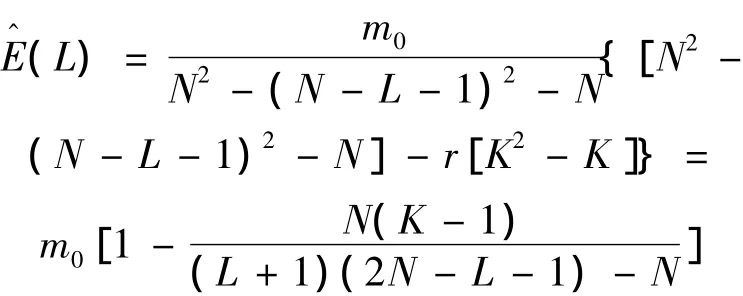
2)当1≤L+1≤K时

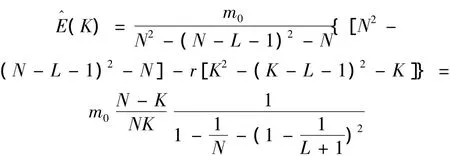
综合以上两种情况可以进一步得到结论:

2)从邻接矩阵带状结构可见，第1个和最后一个计算节点需要进行外部通信的单元总数为，其它计算节点需要进行外部通信的单元总数为

3)由于计算节点间的外部通信比计算节点内部通信耗时多，因此各个计算节点上需要进行外部通信单元总数减少(转成内部通信)，亦即减少了外部通信量，从而可以提高各个计算节点的计算效率。

因此，减小单元邻接矩阵的带宽，可以达到减小外部通信量，从而达到提高并行计算效率的目的。

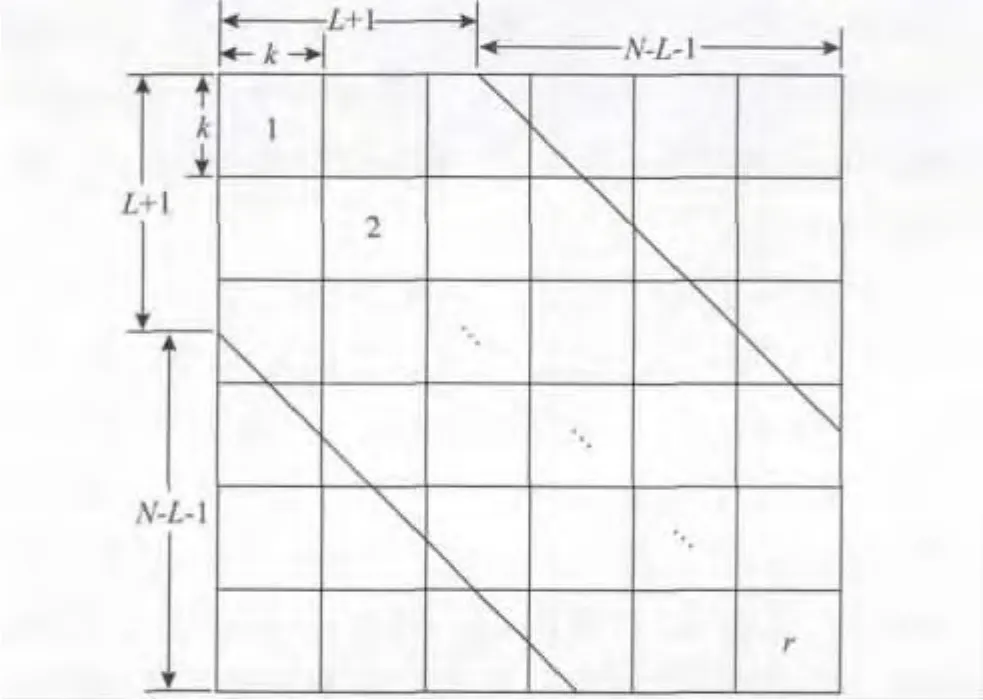
图1 邻接矩阵示意Fig.1 Connectivity matrix sketch map

2 减小邻接矩阵带宽的AD算法

2.1 AD算法简介

AD算法［12］根据如下3个指标的大小决定节点新的编号:(1)节点和:若以当前节点为顶点的单元有m个，对各单元所有顶点的编号求和，然后求出m个单元顶点编号总和，即节点和;(2)节点商:节点和除以m得到的商称为节点商;(3)最大最小编号和:若以当前节点为顶点的单元中，最大的顶点编号与最小的顶点编号之和。

“三农”主持人首先应该是对农村、农民、农业有感情的人。熟悉广播节目的听众都知道，并不是声音甜美就是亲切，并不是语言朴实就是贴心，亲切和贴心都源自节目的编播人员对听众的情感。

AD算法分为2个阶段:第1阶段使用节点商和最大最小编号和作为排序指标，按升序排列，直到整体的迭代步数大于最大迭代次数，或者带宽序列中相邻3次数值相同时转入第2阶段;第2阶段使用节点和及节点商作为排序指标，按升序排列，直到满足类似于第1阶段的终止条件。

2.2 减小单元邻接矩阵带宽的AD算法

最初设计AD算法主要是为了减少矩阵储存量，其手段是通过对节点编号进行优化，使得矩阵带宽减小而达成目的。通过前面对单元邻接矩阵带宽与并行计算效率间的关系分析得到，减小单元邻接矩阵的带宽，可以达到减小外部通信量，从而提高并行效率的目的。因此，为了提高并行计算效率，基于AD算法思想，通过引进类似节点商的单元商对单元编号进行优化，使得矩阵带宽减小，从而设计了一种减小单元邻接矩阵带宽的AD算法。

仿照优化节点编号的AD算法，引出如下变量:单元和:若与当前单元有通信关系的单元有m个，对这m个单元的编号求和，该和称为单元和;单元商:当前的单元和除以与当前单元有通信关系的单元总数(m)得到的商称为单元商。减小邻接矩阵带宽的AD算法的排序指标:AD算法的每阶段均由两个指标进行升序排列，存在序号振荡现象［14］，在一定程度上降低了算法的效率。此外，2个阶段之间也存在类似问题，即在第1阶段排好的节点编号到第2阶段时，由于指标的变更，有可能局部次序被打乱，从而在一定程度上降低了算法的效率。为了避免AD算法存在的相互矛盾和震荡问题，文中在此只采用单元商作为减小邻接矩阵带宽的AD算法的排序指标。

减小邻接矩阵带宽的AD算法终止条件:首先引入如下3个变量:

1)逆序比值Wn:按单元序号检查前后相邻两单元的单元商，如果后一单元商比前一单元商小，则称为一个逆序，所有逆序的总数与单元总数的比值称为逆序比值;

2)半带宽L:令当前单元与离它最远的相关单元的编号差为L0，所有单元中最大的L0则为半带宽;

3)最大单元商差 ΔA:ΔA=max(|A(i)－A0(i)|)，i=1，2，…，n，A(i)，A0(i)分别表示本次迭代、前次迭代时单元i的单元商。

减小单元邻接矩阵带宽的AD算法如下:(1)根据数值计算方法需要调用其它单元数据的情况，建立单元邻接矩阵;(2)根据单元邻接矩阵，计算各单元的单元商;(3)根据单元商的大小对单元进行重新排序，记录新旧单元编号互相对应的关系;(4)根据新旧单元编号的对应关系，以及原单元邻接矩阵的信息，得到新单元编号下的邻接矩阵;(5)计算逆序比值、半带宽以及ΔA，如果满足算法的终止条件转(6)，否则转(2);(6)程序结束，输出结果。

2.3 基于AD算法的区域剖分法

2.3.1 按单元序号和属性的区域剖分法 按序号法(见1中定义)进行区域剖分，虽然能控制各子区域单元数量近似相等，但由于不同属性单元(如边界单元、内单元)需要的计算时间是不同的，为了平衡各计算节点上的负载，在单元编号顺序基础上，需进一步考虑单元属性的影响。假设网格总数为N，计算节点个数为r，网格单元属性有m种，不同属性的单元数量分别为 n1，n2，…，nm，在序号法的基础上，给出一种改进算法。该算法具体思想是，对于任意的第j种属性单元(j=1，2，…，m)，按数量 kj=［nj/r］将该类型单元按顺次分配到各计算节点，尽量使各计算节点上每种类型单元的数量接近相等，且各节点上的单元总数接近N/r，各节点上的单元数总和仍为N。该算法称为按单元序号和属性的区域剖分法，简称序号属性法。

2.3.2 基于AD算法的区域剖分法 序号属性法一般能得到较好的分裂结果，各计算节点上的执行时间达到了大体均衡的效果。但该方法没有考虑外部通信量的问题，因此使用该区域剖分方法产生的外部通信量可能较大，在一定程度上影响了并行效率。因此在进行序号属性法之前，引入减少单元邻接矩阵带宽的AD算法对单元编号进行优化，以期尽可能减小邻接矩阵的带宽，进而减少外部通信量，达到并行效率的进一步提高，这就是基于AD算法的区域剖分法(简称AD分裂法)思想。

具体算法由两部分组成:(1)根据邻接矩阵情况，利用减小单元邻接矩阵带宽的AD算法对单元编号进行优化;(2)利用序号属性法进行区域剖分。

3 算例

测试平台为win 732位操作系统，2G内存的奔腾E5400台式机。算例以研究全球潮波运动为背景，基于球面二维浅水波方程的离散求解WENO方法，计算单元采用的是只具有陆地边界，而无水边界的球面二维无结构网格单元。由于离散格式的需要，计算当前单元信息时不仅要用到第1层相邻单元的信息，同时还要用到第2层相邻单元总共9个相邻单元的信息(称为大模版，见图2)。

对于陆地边界单元需要利用镜像法构造虚拟单元并计算虚拟单元的物理量的值，故其计算时间会远大于内单元的计算时间，区域分裂时必须区别对待内单元和边界单元。

在该数值模拟方法中，内单元物理量计算时间t1=3.187 5×10－6s;边界单元物理量计算时间t2=3.203 125×10－4s;一个单元上物理量的内部和外部通信时间分别为 t3=3.125 × 10－8s，t4=3.906 25 ×10－6s。子计算节点 i上的执行时间为:，其中分别表示子计算节点i上的内单元、外单元、内部通信以及外部通信的单元数量。

以下2个算例涉及到的计算网格单元，都是借助于地表水模拟软件(Surface Modeling System，SMS)生成的全球无开边界的二维无结构网格单元中抽取的部分区域上的网格单元。

算例1 抽取的部分区域上的网格单元数量为54 311个，区域示意如图3所示。采用不同数量的计算节点，分别运用序号法、序号属性法以及目前使用较广的Metis软件多层次K路图分区法，与AD分裂法进行比较，所得结果如表1所示。在计算节点数为4时，应用不同的区域剖分方法，所得区域剖分后的效果如图3～6所示。图上4种灰度分别代表不同计算节点上的计算单元。

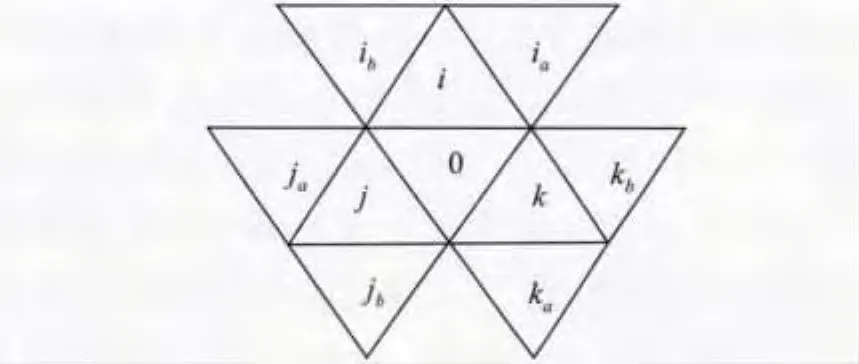
图2 经典计算单元模板Fig.2 Classic cellcom puting template

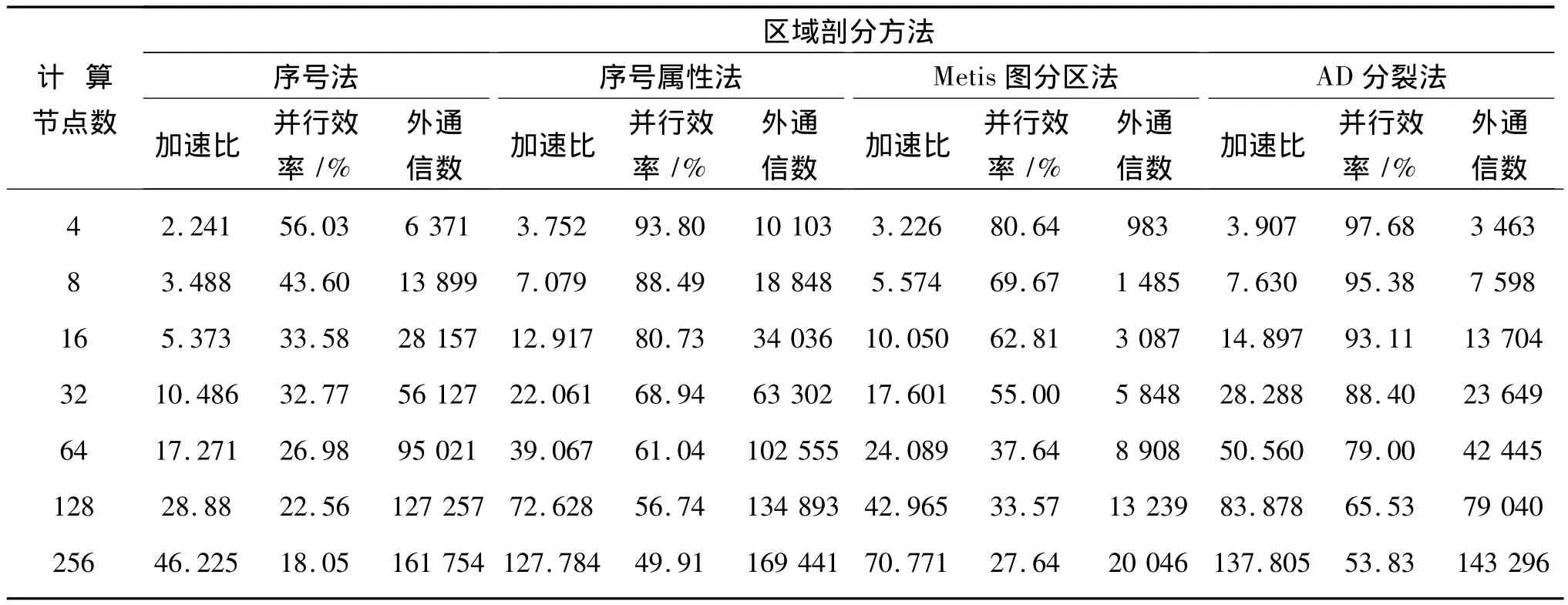
表1 算例1中不同数量计算节点下的区域剖分效果Tab.1 Dom ain decom position result of different processors in example1

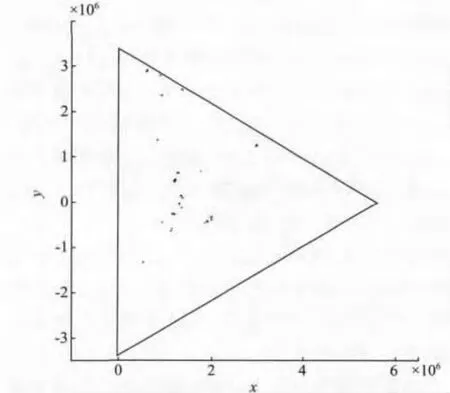
图3 海域岛屿分布Fig.3 Seaisland distribution map

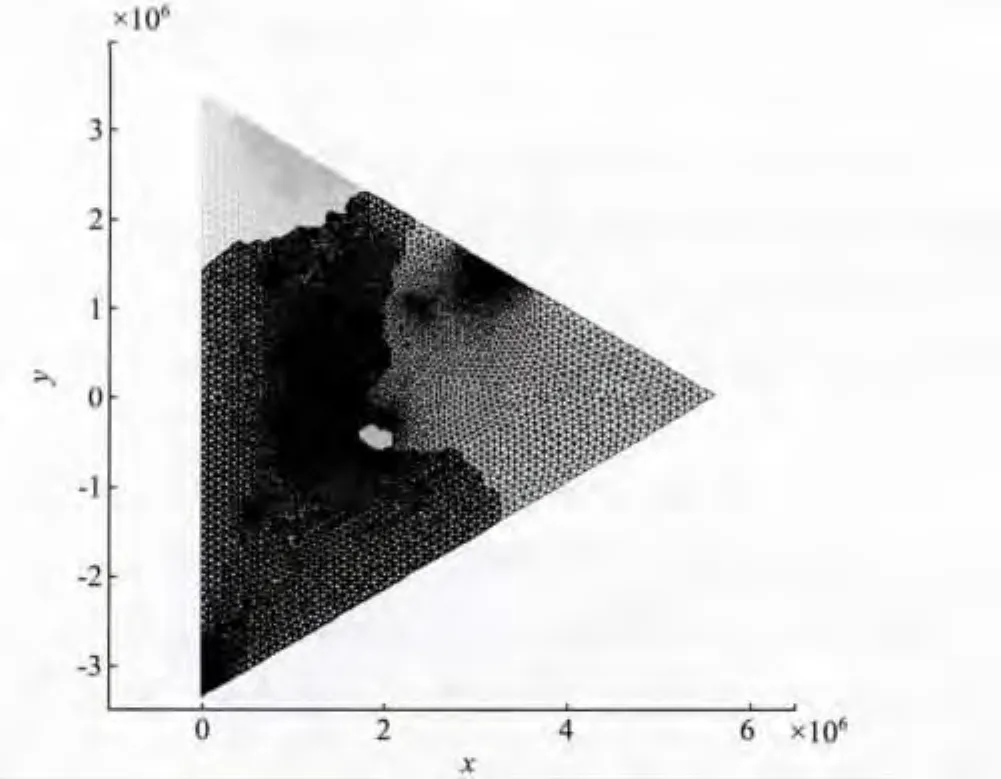
图4 4个计算节点Metis图分区法区域剖分结果Fig.4 Result of Graph Partitioning method by metis in 4 processors

算例2 抽取的部分区域上的网格单元数量为588 755个，其网格单元数量约为算例1的10倍。采用不同数量的计算节点，分别运用序号法、序号属性法以及目前使用较广的Metis软件多层次K路图分区法，与AD分裂法进行比较，所得加速比、并行效率和外通倍数的结果如表2所示。

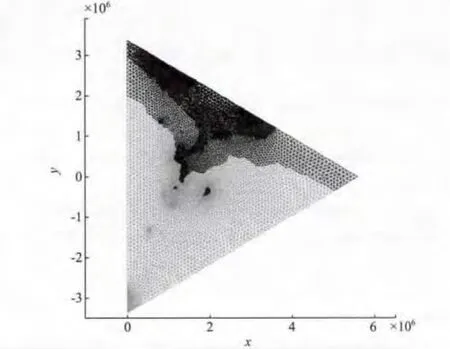
图5 4个计算节点序号属性法区域剖分结果Fig.5 Result of the serial number and property method in 4 processors

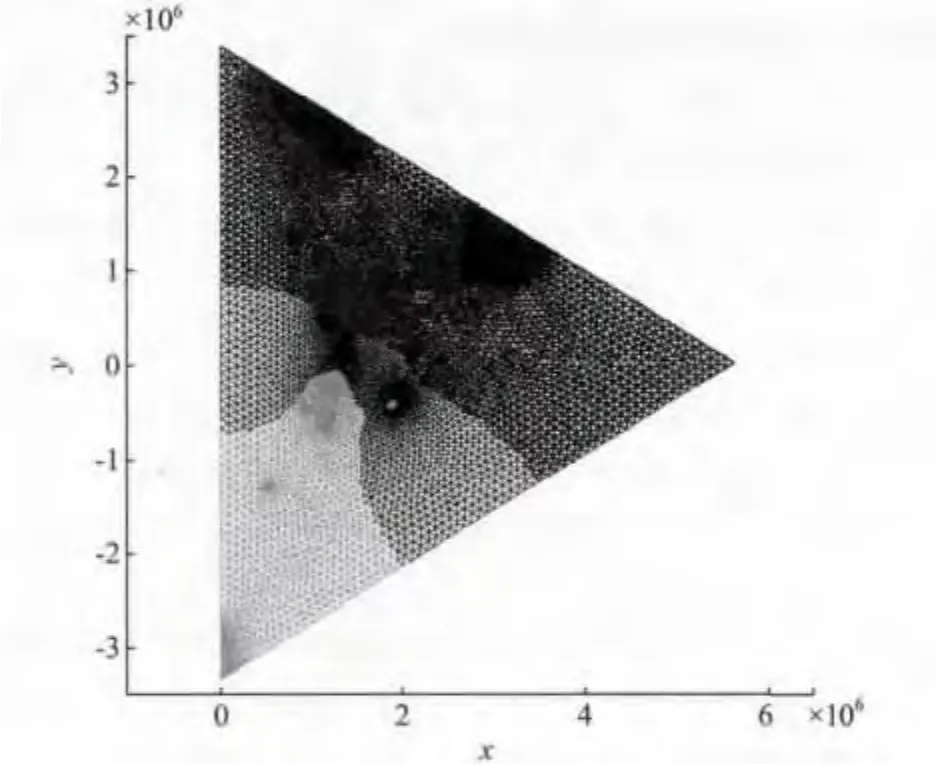
图6 4个计算节点AD分裂法区域剖分结果Fig.6 Result of AD domain decom position method in 4 processors

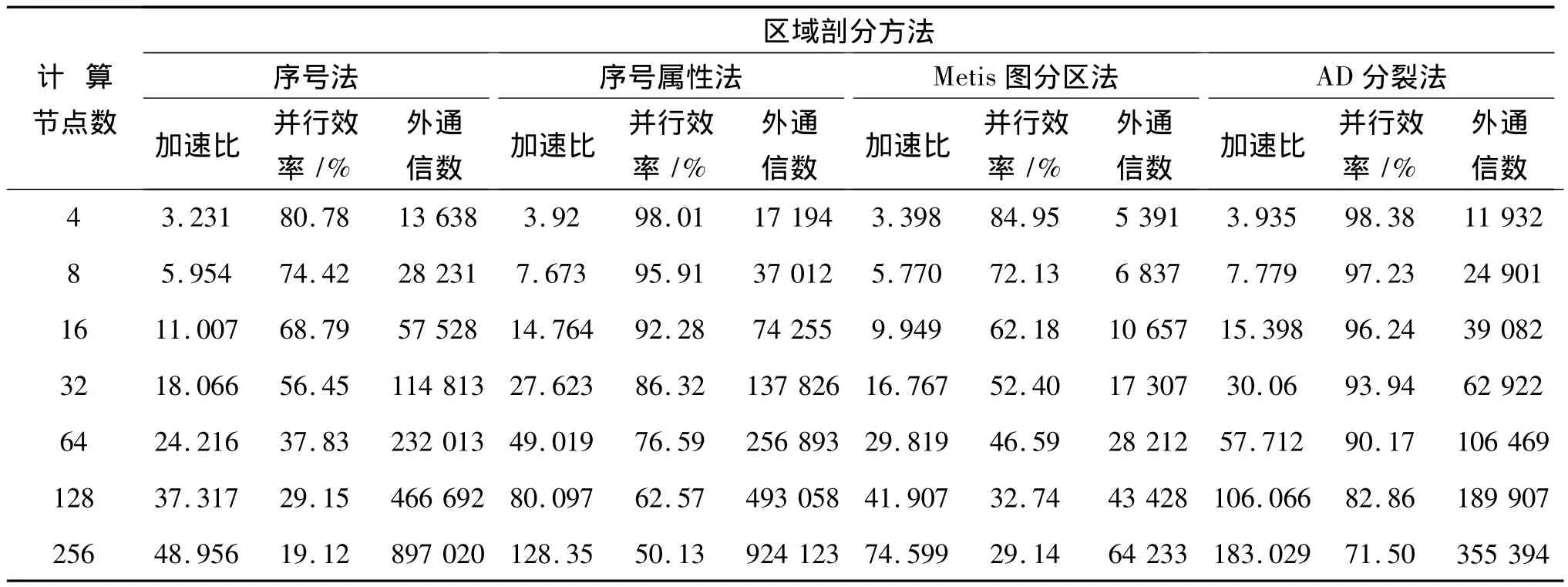
表2 算例2中不同数量计算节点下区域剖分结果Tab.2 Dom ain decom position result of different processors in exam p le 2

以上结果表明，将网格单元进行序号法分裂时，虽然简单迅速，但并行效率不高。序号属性法得到的并行效率有提高，但外通信单元数量较多，不利于并行效率的提高。Metis软件图分区法的主要目的是使各个计算节点上的单元数量相等，且外通信数量尽量少，但是对于采用模拟间断水流的高精度WENO数值模型，边界单元由于需要构建虚拟单元以及赋值，其计算时间远大于内单元;Metis软件没有区别对待内单元以及边界单元，分裂结果中各个计算节点上内单元与边界单元个数不均衡，使得各个子计算节点执行时间不均衡，导致并行效率不高。AD分裂法能保证各计算节点在负载平衡的基础上，有效减少外部通信单元数量，该方法考虑了内单元与边界单元的差异，最后各个计算节点上的执行时间大体均匀，从而得到更高的并行效率。从图6可以看出，AD分裂法得到的图像中各子区域内单元相对集中，各计算节点边界单元个数均衡。当对大数据进行分裂时，AD分裂法也可以得到较高的并行效率，这一定程度上说明该方法在处理大数据时具有可行性与有效性。

4 结语

在AD算法优化编号的基础上对网格单元利用序号属性法进行区域剖分，能得到较高的加速比与并行效率。通过对高达59万个无结构网格单元进行区域剖分试验，结果表明利用AD分裂法进行区域剖分，确实能使各计算节点的负载较快速趋于平衡，得到高加速比与并行效率的区域剖分结果，因此该方法是一种可用于大数据量的网格单元进行区域剖分的可行且有效的方法。

［1］Lohner Rainald.A parallel advancing front grid generation scheme［J］.International Journal for Numerical Methods in Engineering，2001，51(6):663-678.

［2］司海青，王同光，成娟.非结构网格上Eluer方程的区域分裂算法及其并行计算［J］.空气动力学学报，2006，24(1):102-108.SIHaiqing，WANG Tongguang，CHEN Juan.Domain decompositions and parallel algorithms to solve Euler equations on the unstructured grid［J］.Acta Aerodynamica Sinica，2006，24(1):102-108.(in Chinese)

［3］ Henrickson B，Kolda TG.Graph partitioningmodels for parallel computing［J］.Parallel Computing，2000，26(12):1519-1534.

［4］ Pothen A，Simon H，Liou K P.Partitioning sparsematrices with eigenvectors of graphs［J］.SIAM JMath Anal Appl，1990，11(3):430-452.

［5］ Simon H D.Partitioning of unstructured problems for parallel processing［J］.Comput Eng，1991，2(2/3):35-148.

［6］周春华.并行计算中一种非结构网格分割方法［J］.航空学报，2004，25(3):229-232.ZHOU Chunhua.A method of non-structured mesh partition for parallel computation［J］.Acta Aeronautica et Astronautica Sinica，2004，25(3):229-232.(in Chinese)

［7］ Walshaw C，Cross M.Mesh partitioning:a multilevel balancingand refinement algorithm［J］.SIAM Journal on Scientific Computing，2000，22(1):63-80.

［8］ Karypis G，Kumar V.A fast and high qualitymultilevel scheme for partitioning irregular graphs［J］.SIAM Journal on Scientific Computing，1998，20(1):359-392.

［9］Catalyurek U V，Boman E G，Heaphy R，et al.Hypergraph based dynamic load balancing for adaptive scientific computations［C］//Proc of IEEE International Conference on High Performance Computing.Long Beach:IEEE Press，2007:367-380.

［10］ Trifunovi A，KnottenbeltW J.Parallelmultilevel algorithms for hypergraph partitioning［J］.Journal of Parallel and Distributed Computing，2008，68(4):563-581.

［11］ Kernighan BW，LIN S.An efficient heuristic procedure for partitioning graphs［J］.The Bell System Technical Journal，1970，49(2):291-307.

［12］ Akhras G，DhattG.An automatic node relabeling scheme forminimizing amatrix or network bandwidth［J］.International Journal for Numerical Methods in Engineering，1976，10(4):787-797.

［13］赵玉静，吴建军，符文贞.板料成形数值模拟中网格节点编号优化［J］.锻压装备与制造技术，2009，44(6):73-75.ZHAO Yujing，WU Jianjun，FU Wenzhen.An algorithm for optimizing the node number of the numerical simulation in sheet forming［J］.China Metalforming Equipment and Manufacturing Technology，2009，44(6):73-75.(in Chinese)

［14］胡志宇，邹琦，陈涛.改进的有限元网格编码AD算法［J］.三峡大学学报:自然科学版，2009，31(2):63-65.HU Zhiyu，ZOUQi，CHEN Tao.An improved AD algorithm for finite elementsmesh code optimization［J］.Journalof China Three Gorges University:Natural Sciences，2009，31(2):63-65.(in Chinese)