Mn掺杂Ga As稀磁半导体的第一性原理研究

张云丽,杨建国,朱自强,周小东,巫洪章,谭明秋

稀磁半导体(DMS)是指利用3d族过渡金属或者4f族稀土金属的磁性离子取代Ⅱ-Ⅳ族、Ⅳ-Ⅵ族、Ⅲ-Ⅴ族等半导体中的部分带正电的离子而形成的新型半导体材料,如Zn1xMnxSe,Sn1-xMnxTe,Zn1-xMnxO等.稀磁半导体因兼有半导体及金属共同特性使其在电子器件和磁性方面有着很广泛的应用[1,2],因此,无论从理论还是应用上研究稀磁半导体都有重要的意义,稀磁半导体已成为近年来研究的热点[37].Ga As是一种重要的半导体材料,禁带宽度(能隙)1.4 e V与太阳光谱匹配好,具有熔点较高(1 238℃),耐高温等较好特性使其在电池、半绝缘高阻材料、集成电路衬底、探测器等方面有着广泛应用.1996年,Ohno H等用低温分子束外延(LT-MBE)方法研究制备出基于Ⅲ-Ⅴ族化合物Ga As新型稀磁半导体化合物Ga1-xMnxAs(Mn组分x在0.015～0.07范围)[8],(Ga,Mn)As的发现标志着稀磁磁性半导体的新时代.(Ga,Mn)As因既具有Ⅲ-Ⅴ族化合物半导体Ga As的特性,又具备铁磁化合物的特点,并与Ⅲ-Ⅴ族异质结技术有_很好的兼容性使其具有独特吸引力,因此,最近涌现出了人们对于(Ga,Mn)As稀磁导体的研究涌现出热潮[810].人们对Mn掺杂Ga As稀磁半导体材料的制备、结构、和磁性做了大量实验研究[11-19],然而有关Ga1-xMnxAs的理论研究相对较少,本文采用基于密度泛函理论(DFT)的第一性原理对Mn掺杂Ga As稀磁半导体的稳定结构、磁序特点、及电子结构研究,发现Mn掺杂Ga As体系的稳定构型,为得到Ga1-xMnxAs稳定构型、磁性来源、解释Mn掺杂Ga As体系导致其具有稀磁半导体特性的原因,为进一步进行相关研究提供理论引导,并可基于此探求了其应用前景.

1 结构模型和计算方法

1.1 结构模型

Ga As的晶体结构如图1,这个化合物的空间群是F-43M(No.216).实验上的晶格常数是a=b=c=5.763 09Å,每个晶胞模型中含有4个Ga原子和4个As原子.为了构造实验上Mn掺杂Ga As体系的掺杂浓度[8](0.015～0.07)范围内的掺杂体系Ga1xMnxAs,基于Ga As构造了2×2×2的超晶胞,如图2,其中两个Ga原子被Mn原子取代,得到掺杂浓度为2/32,相当于实际取Mn掺杂浓度为6.25%.通过将图2中的上下面和左右面上的Mn原子分别取相同的磁序取向、相反的磁序取向及不考虑其磁性的情况下得到Ga1xMnxAs(x=0.0625)的铁磁(FM)、反铁磁(AFM)、顺磁(NM)三种不同的构型.

图1 Ga As的晶体结构

图2 Ga1x Mn x As的晶体结构(x=0.0625)

1.2 计算方法

关于Ga1xMnxAs(x=0,0.0625)体系的电子结构域磁性特征的计算采用的是VASP计算模拟程序包[20],电子间的交换关联势是来自该程序包基于投影缀加平面波[21]的Perdew-Burke-Ernzerhof(PBE)势[22].Ga1xMnxAs体系中的Ga,Mn,As的价电子分别取4s24p1,3d64s1和4s24p3.整个工作中平面波截断能取350 e V.K点是通过使Monkhorst软件来自动得到的[23].计算中的K点分别取11×11×11,5×5×5的Monkhorse-Pack网格来优化图1和图2晶胞和超晶胞模型,总能量差小于105e V时自洽循环计算停止,而对于电子结构特性相应的计算Monkhorst-Pack网格取优化时的两倍.

2 计算结果与讨论

2.1 Ga As的电子结构

首先计算研究了纯的GaAs晶体的电子结构,包括总体的态密度和各元素的分态密度如图3.从图3可以看出纯净的Ga As晶体的总的态密度图特点.计算结果表明,由于纯净的GaAs是无磁性的,其电子结构是上下对称的,因此可以不研究磁性,只画出其自旋向上的分波态密度.Ga As总的态密度显示出半导体特性(费米面附近态密度在能量区间段内存在零值),带隙约为1.0 e V(费米面(EF)附近态密度为零的能量间隔范围),分波态密度可以显示Ga以As的态密度峰值几乎完全对应,表明Ga和As之间的轨道杂化明显,主要体现共价键特征.在-5 e V到-2.5 e V,As的态密度与Ga的态密度基本相同,在-2.5 eV到0 eV,As的态密度大于Ga的态密度,电子倾向于As离子排布.在0 eV到5 e V内,Ga的态密度大于As的态密度,说明Ga的未占据态较多.

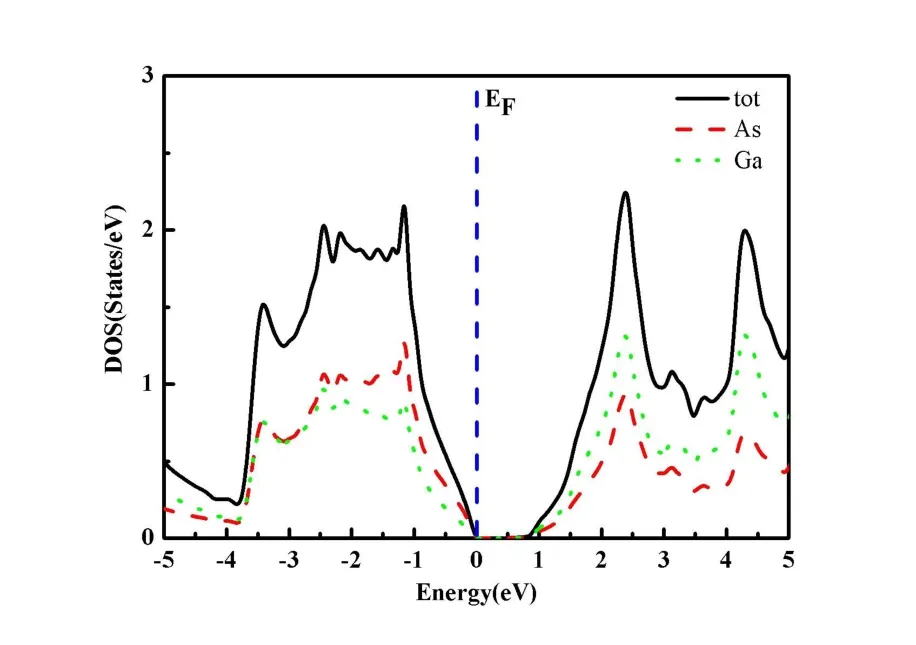
图3 Ga As的电子结构图

2.2 Mn掺杂GaAs的稳定构型、磁性来源

首先针对图2中的上下面和左右面上的Mn原子分别取相同磁序取向、相反磁序取向及不考虑其磁性情况得到Ga1-xMnxAs(x=0.0625)的铁磁(FM)、反铁磁(AFM)、顺磁(NM)三种不同的构型进行了结构优化,基于优化后的结果计算了三种构型下的能量,表1给出了Ga1xMnxAs(x=0.0625)体系在不同构型下的能量.

表1 _Ga1-x Mn x As(x=0.0625)在不同构型下的能量__

由于物质本身能量越低,其键能越大,破坏这种物质所需要的能量就越多,所以越难破坏,也就是物质稳定.在数据中比较可知,FM构型(掺杂的Mn原子磁序一致)的能量是最低的,因此FM构型是最稳定的构型.在磁性方面,通过研究发现,对于构建的Ga1xMnxAs(x=0.0625)晶体模型的总磁矩为8.000 7μB,而一个Mn原子的磁矩为3.702μB,在模型图2中一个晶包中含有2个Mn原子,所以Mn的磁矩为3.702×2=7.404μB,计算结果表明Mn掺杂的Ga As晶体的磁性主要来自于Mn元素.

2.3 Mn掺杂GaAs的电子结构

为了研究Mn掺杂Ga As体系对其电子结构特性的影响,基于Ga1-xMnxAs(x=0.0625)体系的稳定构型基础上进一步计算研究Ga1xMnxAs(x=0.0625)体系的电子结构,为了和纯的Ga As作对比,图4给出了其总的态密度、各元素的分态密度,由于Ga1xMnxAs(x=0.0625)体系的磁性主要来源于Mn原子,图5进一步从Mn的分波态密度研究、分析并解释了其磁性主要来源.

图4 Ga1x Mn x As(x=0.0625)的电子结构图

图5 Ga1x Mn x As(x=0.0625)体系中Mn的分波态密度图

从图4可以看出Mn掺杂的Ga As晶体态密度在-5～5 e V能量范围内总态密度和原子分态密度已不具有对称性,自旋向上的态密度在费米面(EF)上不为零,即自旋向上的态显示金属特性,自旋向下的态密度显示出半导体性质,因此计算结果表明Ga1xMnxAs(x=0.0625)具有稀磁半导体特性.进一步分析图4可以看出Mn原子分态密度最不具有对称性,因而从Ga1xMnxAs(x=0.0625)的原子分态密度同样可以得出Ga1-xMnxAs(x=0.0625)体系的磁性主要来源于Mn原子.为了明确对于Mn原子的磁性主要来自哪个电子轨道,图5给出了Mn原子的总的态密度及s,p,d轨道的各分波态密度,从图5可以看出在-5～5e V能量范围内Mn的总电子态密度几乎完全来源于3d轨道,且不对称性较强,可以看出Mn原子的磁性主要来源于Mn原子的3d轨道电子的贡献.

2.4 Mn掺杂Ga As稀磁半导体的应用前景

Mn掺杂Ga As稀磁半导体是半导体学与磁学相结合发展的产物,它的制备使非磁性半导体磁性化,使人们对半导体中的电子电荷与电子自旋的研究相结合,为开辟半导体技术新领域以及制备新型电子器件提供了有利的条件.

当前对于Mn掺杂的Ga As稀磁半导体的研究尚处于起步阶段,但已经展示出其广阔的应用前景.主要体现在Mn掺杂Ga As稀磁半导体材料可以将磁性金属与半导体相连接,用来作为两者间的界面层,实现自旋极化的载流子往非磁性半导体中的注入,为研究非磁性半导体中的载流子自旋奠定了基础.另一方面Mn掺杂的Ga As稀磁半导体材料把半导体异质与铁磁性相联系,将产生新型电子器件.目前研究发现这种完全由半导体构成的磁性层表现出磁阻现象,可能具有磁性存储和记忆功能.同时,半导体多层结构可以实现半导体集成.

Mn掺杂的GaAs稀磁半导体材料出现不久,但它的发展迅速.人们的研究主要集中在基础方面,目前正转向基础研究和应用相结合的方面.今后的工作将继续深入对Mn掺杂的GaAs稀磁半导体材料特性的研究,并应用到实践中去.

3 结束语

本文基于密度泛函(DFT)理论框架下的第一性原理计算研究了 Mn掺杂GaAs体系.首先,通过计算得到了纯的Ga As晶体的半导体性质的电子结构特点;其次,通过比较不同构型下Mn掺杂Ga As晶体的能量得到了Mn掺杂Ga As体系的稳定构型,基于稳定构型计算得到Mn掺杂Ga As稀磁半导体磁性主要来自Mn原子;最后,研究了稳定构型下Mn掺杂Ga As体系电子结构特点,发现其稀磁半导体特性,基于此分析阐述了Mn掺杂的Ga As稀磁半导体的应用前景,此结果为相关稀磁半导体材料研究提供一定的引导和帮助.

参考文献:

[1]H.Ohno.Making Nonmagnetic Semiconductors Ferromagnetic[J].Science,1998,281(14):951.

[2]S.A.Wolf,D.D.Awschalom,R.A.Buhrman,et al.Spintronics:a spin-based electronics vision for the future[J].Science,2001,294(16):1488.

[3]T.Dietl.A ten-year perspective on diluted magnetic semiconductors and oxides[J].Nature Mater.,2010,9:965.

[4]M.Marques,L.G.Ferreira,L.K.Teles,et al.Magnetic properties of GaN/MnxGa1xN digital hetero structures:First-Principles and Monte Carlo calculations[J].Phys.Rev.B,2006,73(22):224409.

[5]C.Liu,F.Yun,H.Morkoc.Ferromagnetism of ZnO and Ga N:A review[J].Journal of Materials Science:Materials in electronics,2005,16(9):555.

[6]T.Sasaki,S.Sonoda,Y.Yamamoto,et al.Magnetic and transport characteristics on high Curie temperature ferromagnet of Mn-doped Ga N[J].J.Appl.Phys.,2002,91(10):7911.

[7]K.Sato,L.Bergqvist,J.Kudrnovsky,et al.Firstprinciples theory of diluted semiconductors[J].Rev.Mod.Phys.,2010,82(12):1633.

[8]H.Ohno,A.Shen,F.Matsukura,et al.(Ga,Mn)As:A new diluted magnetic semiconductor based on Ga As[J].Appl.Phys.Lett.,1996,69(3):363.

[9]R.Shioda,K.Ando,T.Hayashi,et al.Local structures of III-V diluted magnetic semiconductors Ga1xMnxAs studied using extended x-ray-absorption fine structure[J].Phys Rev B,1998,58(3):1100

[10]H.Ohnoa,F.Matsukuraa,Y.Sugawaraa,et al.Epitaxy of(Ga,Mn)As,a new diluted magnetic semiconductor based on Ga As[J].Journal of Cryst al Growth,1997,175/176(2):1069-1074

[11]郭旭光,陈效双.(Ga,Mn)As体系中Mn无序对其电子结构及磁性影响的第一性原理研究[J].物理学报,2004,53(5):1516-1519.

[12]陈余,关玉琴.3d过渡金属掺杂GaAs的居里温度研究[J].内蒙古工业大学学报,2009,28(3):188-192.

[13]蔺何,段海明.Ga As掺杂3d过渡族金属材料的局域电子结构和磁性[J].中国科学,2008,38(5):513 522.

[14]陈启燊,雷天民.Ga As第一性原理研究[J].电子科技,2009,22(4):69-71.

[15]关玉琴,陈余,赵春旺.Mn和Cr共掺杂对Ga As居里温度的影响[J].功能材料,2010,41:94-96.

[16]刘芳芳,杨瑞霞,刘立浩,等.半磁半导体材料(Ga,Mn)As[J].河北工业大学学报,2002,31(6):35-42.

[17]刘力锋,杨瑞霞,郭惠.基于Ga As的新型稀磁半导体材料(Ga,Mn)As[J].半导体情报,2001,38(6):25-30.

[18]姬长建,张成强,冯素华,等.稀磁半导体(Ga,Mn)As的物理性质研究[J].山东教育学院学报,2010,142(6):21-24.

[19]陈余,关玉琴,赵春旺.稀磁半导体材料居里温度的极值点[J].发光学报,2009,30(5):702-705.

[20]G.Kresse and J.Furthmüller.Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set[J].Phys.Rev.B,1996,54(16):11169.

[21]P.E.Blöchl.Projector augmented-wave method[J].Phys.Rev.B,1994,50(24):17953.

[22]G.Kresse and D.Joubert.From ultrasoft pseudopotentials to the projector augmented-wave method[J].Phys.Rev.B,1999,59(3):1758.

[23]H.J.Monkhorst and J.D.Pack.Special points for Brillonin-zone integrations[J].Phys.Rev.B,1976,13(12):5188.