HTPB复合固体推进剂粘弹性应变能及非线性本构模型

张 晓，郑 坚，彭 威，张前图

(军械工程学院，石家庄 050003)



HTPB复合固体推进剂粘弹性应变能及非线性本构模型

张 晓，郑 坚，彭 威，张前图

(军械工程学院，石家庄 050003)

为了准确表征HTPB复合固体推进剂在有限变形条件下的力学性能，针对推进剂粘弹性应变能及本构模型进行研究。提出了推进剂粘弹性应变能函数和非线性本构方程的一般形式，并通过一元非线性回归方法拟合不同应变率下的拉伸试验数据，得到了材料参数关于应变率的函数，并由此建立了推进剂单轴拉伸变形下的应变能函数和本构方程，预测了不同应变率下的应力曲线，与试验结果和已有模型的预测结果进行了对比。结果表明，材料参数与应变率之间呈现幂函数关系；推进剂应变能密度随变形量的增大呈非线性单调增长，同一变形条件下，应变率越高，推进剂的应变能密度越大；本构方程可准确描述推进剂拉伸变形的应力应变关系，且尤其适用于表征低应变率下，材料在有限变形内的粘弹特性。

HTPB推进剂；应变能；非线性回归；参数函数；本构方程；变形

0 引言

端羟基聚丁二烯(HTPB)推进剂是一种以高聚物为基体的多组分、高延伸率复合材料，具有强烈的非线性粘弹特性[1]，且推进剂的力学性能主要取决于基体。针对高聚物非线性粘弹性行为的研究，Leaderman[2]最早指出非线性粘弹行为可以在小应变时发生，并在修正Boltzmann线性叠加原理的基础上给出了半经验公式；Ward和Onat进一步对叠加原理进行了修正，得到了非线性粘弹性的多重积分型本构关系[3]；Shcapery[4-6]、Findley[7]、Bernstein等[8]做了大量工作，分别发展了热力学本构关系、幂律关系和BKZ理论。对于复合固体推进剂的线性粘弹性，国内外已做了大量研究，并已相当成熟；同时，国内外在推进剂非线性力学行为方面，也做了很多卓有成效的工作，但无论理论方面、数值模拟方面，还是精确解方面，都远不如前者充分和深入，尚有很多问题需要进一步探讨。由于不满足Boltzmann线性叠加原理，对推进剂材料的非线性粘弹性行为进行描述，要运用更加普遍的理论。Gyoo等[9]基于Vratsanos-Farris模型提出了一个含Mullins效应和损伤脱湿效应的三维非线性粘弹性模型；龚建良等[10]根据热力学能量守恒定律，研究了HTPB推进剂增强粒子脱湿引起的非线性行为，确立了临界脱湿应变方程；邓凯等[11]将Shcapery非线性粘弹本构模型与Perzyna非线性粘塑本构模型结合，建立了HTPB推进剂非线性粘弹塑性本构方程；张永敬等[1]结合Monte-Carlo方法，用Shcapery蠕变型非线性粘弹本构模型，分析了推进剂的蠕变行为；彭威等[12]曾经从微观尺度对推进剂的非线性本构关系进行表征。

从应变能函数出发研究弹性理论，在橡胶、生物膜等材料中已得到广泛应用[13-15]。粘弹性材料由于具有率相关性、历史相关性和应力松弛等特性，其应变能不仅是应变不变量(或主伸长比)的函数，还应强烈依赖于时间。Hrapko等[16]基于运动学框架导出了非弹性变形的发展方程，并在Mooney-Rivlin模型的基础上进行修正，结合纯剪切试验，建立了脑细胞薄膜的粘弹应变能函数。真实材料或多或少存在蠕变、松弛、迟滞等现象，即表现出粘弹性，Yang等[17]就曾指出，橡胶在高应变率变形条件下，同时表现出超弹性和粘弹性。因此，研究粘弹性应变能表达式并用于建立本构方程，对描述材料的真实特性，发展非线性粘弹性理论，具有重要的现实意义。HTPB推进剂是典型的粘弹性材料，在许多实际应用中，其力学行为表现出明显的非线性。因此，研究其变形行为的应变能，准确表征应力和应变之间的关系，对于装药结构完整性的评估，具有很高的应用价值，而国内外关于这方面的报道很少。

本文给出了HTPB推进剂粘弹性应变能的一般形式，并运用应变能函数表征复合固体推进剂应力和应变之间的关系，避开了复杂的物理本质和发展过程，建立的本构模型能准确描述推进剂材料的力学行为，且比以往更有利于工程运用。

1 变形的几何描述

对于任意连续介质，在外力的作用下发生连续变形，物质内任意质点从参考构形变化到瞬时构形，在t时刻的瞬时位置矢量可表示为

x=x(X,t)

(1)

变形梯度张量F定义为

(2)

由式(2)有：

dx=F·dX

(3)

式(3)表明，变形梯度张量F把参考构形中的每一个微线元矢量dX映射成瞬时构形中的微线元矢量dx。因此，张量F能够反映一点处变形的全部信息。对于任何一个可逆的张量F，可以有如下的极分解形式：

F=R·U=V·R

(4)

式中R为正交张量，表示纯转动；U与V为正定对称张量，代表纯变形。

但在实际运用中，通常用左、右柯西-格林变形张量B和C描述物体变形，B、C分别定义为

B=F·FT，C=FT·F

(5)

以I1、I2和I3分别代表左、右柯西-格林变形张量B、C的第1、第2和第3不变量，则有

I1=tr(C)=λ12+λ22+λ32

(6)

I3=det(C)=λ12λ22λ32

式中 tr和det分别表示张量的迹和行列式；变量λ1、λ2、λ3是3个主伸长比；λi=1+εi，i=1,2,3，εi表示名义应变的主应变。

为全面描述一点处的变形情况，定义一个量E为

(7)

E称为Lagrange或Green应变张量，求其随体导数，得：

(8)

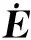
2 模型的建立

2.1 应变能函数

材料变形的应变能(或变形能)是在外载荷的作用下发生变形，而储存在材料中的能量。研究表明，应变能函数能较好表征物体的变形特征，在超弹性材料中，常用的应变能模型有描述橡胶变形行为的Mooney-Rivlin模型、Ogden模型等及描述生物薄膜变形行为的Fung模型、GPR模型等。运用应变能函数描述材料的变形，关键在于应变能函数模型的选择，不同的应变能模型的适用条件和使用范围是不同的。因此，所选应变能函数应尽量准确描述变形行为的真实情况，所建立的应变能函数模型也应详细说明使用条件及范围；另一方面，函数中应包含尽量少的待求参数，以减少拟合所需试验数据。

对于各向同性材料，应变能函数可用左(或右)柯西-格林变形张量B(或C)的主不变量I1、I2和I3或变形梯度张量F的特征值，即主伸长比λ1、λ2、λ3写出：

W=W(I1,I2,I3)或W=W(λ1,λ2,λ3)

(9)

由于复合固体推进剂为接近不可压缩各向同性材料，因此假设推进剂材料不可压缩，且在变形过程中各向同性仍然有效。对于不可压缩材料(I3=1)，可得到：

W=W(I1,I2)

(10)

鉴于推进剂单向拉伸的应力应变曲线与橡胶类材料拉伸响应的S型曲线的前半段形状相同，如图1所示。本文考虑以橡胶类材料的应变能表达式作为函数模型，描述推进剂的拉伸变形，但由于推进剂具有明显的粘弹特性，其应变能函数中的材料参数将不再为恒定值，而是与应变率(或时间)等相关的参数函数。

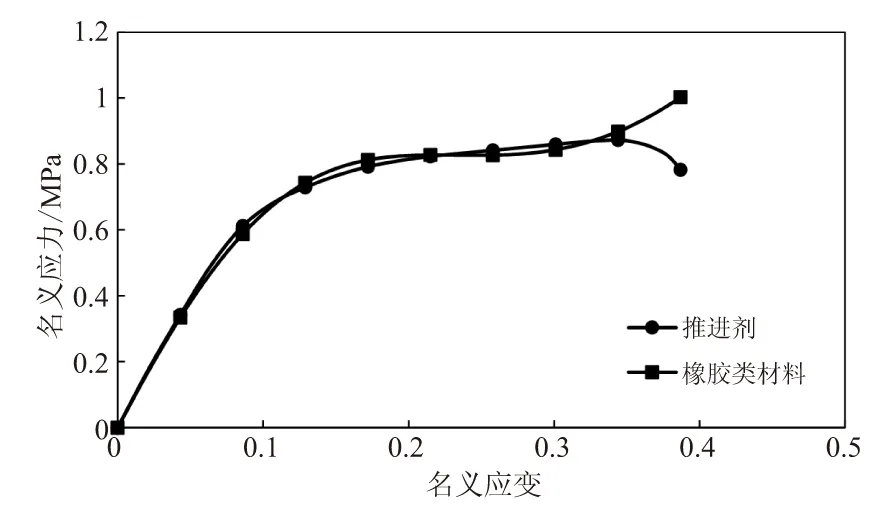
图1 推进剂与橡胶类材料单向拉伸应力应变曲线对比

Fig.1 Comparison between uniaxial tensile stress-strain curves of propellant and rubber-like material

Hart-Smith曾在文献[18]中介绍的用于描述橡胶类材料力学行为的“Exp-Ln”方程形式为

(11)

式中W为应变能；A、a、b为待求材料参数。

“Exp-Ln”方程能够较好描述橡胶类材料的变形行为，且具有较少的材料参数。因此，以式(11)作为推进剂应变能的函数表达式。

函数中的待求参数A、a、b仅为试验数据的拟合系数，不具有任何物理意义。因此，本文所建立应变能函数是对推进剂的力学行为进行唯象描述，不涉及任何有关结构的解释，这对于工程应用和宏观力学研究是足够的。

所建立模型应具有如下特性：(1)能够准确描述推进剂的变形响应，适用于确定的变形模式；(2)待求参数函数的确定需要尽量少的试验。以上将在试验部分进行验证和讨论。

2.2 本构模型

纯力学变形条件下，考虑加载开始时刻为时间零点，t<0时的变形历史的影响可忽略不计。所以，推进剂粘弹应变能函数在同一应变率下的材料参数(A、a、b)将为定值，具有与橡胶等的弹性应变能函数相同的特征。因此，认为此时应变能函数与应力的关系可写成[17]：

(12)

式中σ为Cauchy应力张量；p为静水压力；I为单位张量。

式(12)为不可压缩材料的真实应力(或Cauchy应力)与主不变量(或主伸长比)之间的关系表达式。其中，真实应力σ与变形状态有关，静水压力p可取任意值，其对应的应力分量是不确定的。

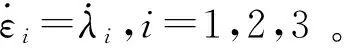
3 试验与分析

采用不同加载速率下的单轴拉伸试验数据拟合材料参数，试验在微机控制五头电子式万能试验机上进行，单轴等速拉伸速率分别为0.5、5、20、100、500 mm/min；同时，进行了2、2 000 mm/min下的单轴等速拉伸试验，用于验证所建立的数学模型。

试验均在环境温度20 ℃、湿度40%条件下进行，试验材料为标准哑铃型试件，标距70 mm，截面10 mm×10 mm。以上试验各进行5组，结果分别为5组试验的平均值。

3.1 材料参数拟合

单轴等速拉伸对试件施加一维应力，假设拉伸方向上主伸长比为λ，则由不可压条件导出：

(13)

Cauchy-Green变形张量的主不变量：

I1=λ2+2λ-1，I2=2λ+λ-2，I3=1

(14)

试件在拉伸方向上σ11=σ，垂直于拉伸方向上σ22=σ33=0。

将式(5)、式(11)、式(13)代入(12)，得：

σ11=-p+2Aλ2{exp[a(I1-3)]-bln(I1-2)}

(15)

σ22=σ33=-p+2Aλ-1{exp[a(I1-3)]-bln(I1-2)}

(16)

又因为σ22=σ33=0

(17)

σ11为真实应力(Cauchy应力)，不可压条件下，名义(工程)应力f11可表示为

(18)

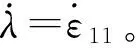
用非线性回归分析方法，拟合拉伸应变率为1.19×10-4s-1(0.5 mm/min)、11.9×10-4s-1(5 mm/min)、47.6×10-4s-1(20 mm/min)、0.023 8s-1(100 mm/min)、0.119 s-1(500 mm/min)的单轴拉伸试验数据，拟合曲线与试验曲线对比见图2。

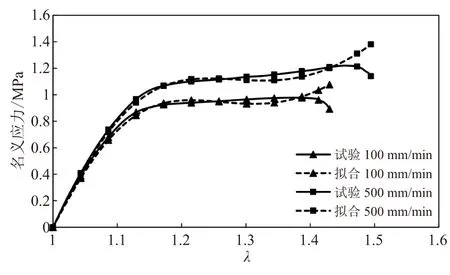
(a)100、500 mm/min

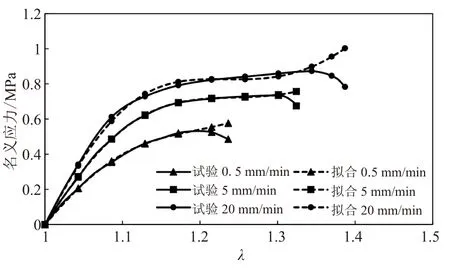
(b)0.5、5、20 mm/min

由图2可看出，拟合结果与试验结果基本吻合，说明本文所提模型能够较好地表征推进剂的拉伸特性。另一方面，图2(a)、图2(b)对比表明，模型对于数据的拟合效果与拉伸速率有关，拉伸速率愈低，拟合效果愈好。因此，所提模型更加适用于描述低应变率下推进剂的粘弹性力学行为。不同应变率下模型参数的取值不同，但呈规律性分布，参数拟合结果见表1。不同应变率下模型参数的散点分布如图3所示。由图3可看出，参数取值与应变率之间呈现非线性相关关系，可考虑作一元非线性回归。根据散点分布趋势线的走势，选取以下2种函数作为理论回归方程：

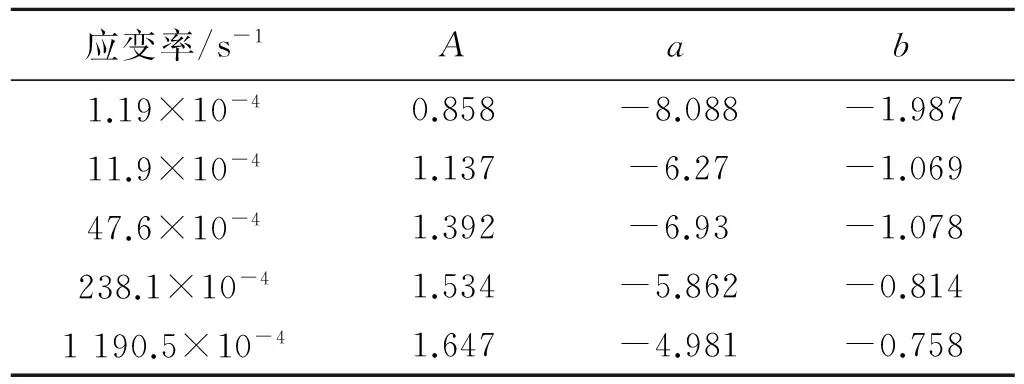
表1 不同应变率下的模型参数Table 1 Model parameters at different strain rate

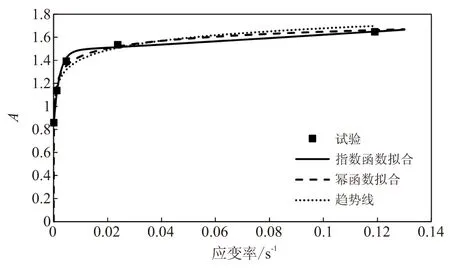
(a)参数A

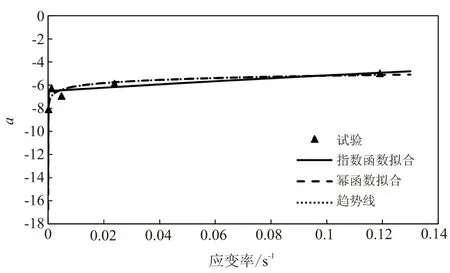
(b)参数a

(c)参数b 图3 模型参数回归曲线Fig.3 Regression curves of model parameters

同时，对多种不同配方HTPB推进剂的参数函数进行了拟合。结果表明，上述方法具有良好的普遍适用性，多种配方的材料参数均可表示为关于应变率的幂函数形式。

(19)

表2 参数函数拟合结果Table 2 Fitting results of parametric functions

代入式(11)，则应变能函数表示为

基于BIM模型，进行空调系统的自动设计。主要由三步组成：（1）空调分区与负荷计算。由BIM模型通过计算导出轻量化模型，进行自动分区与负荷计算，输出房间负荷计算结果、空调系统分区结果、建筑基本几何信息；（2）理想系统的生成。输出理想系统描述文件（包含设备明细，连接关系）；（3）实际系统的生成。修正理想系统描述文件，生成实际空调系统图。在BIM大力发展的时代，通过空调系统的自动设计，来减轻工程师在设计中的繁重劳动，能将更多精力投入在方案的选择上。在实际工程中，减少与建筑、结构设计的时间滞后性，促使各部门之间及时地互联互通。

[1-ln(λ2+2λ-1-2)]-1}

(20)

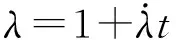
3.2 模型验证

为了验证所建应变能模型和本构模型的准确性，将应变率为4.76×10-4(2 mm/min)、0.476 s-1(2 000 mm/min)的单轴拉伸试验结果与本文模型预测结果、数值计算结果、Mooney-Rivlin模型预测结果以及BKZ单积分本构模型预测结果进行对比，如图4所示。

图4表明，所建模型可较好地预测拉伸速率为2、2 000 mm/min下的名义应力，预测结果优于Mooney-Rivlin模型和数值仿真，与能有效反映应力松弛等粘弹特性的BKZ模型预测结果基本相同，且在2 000 mm/min时，一定程度上优于BKZ模型，验证了模型的准确性。由于所提模型避免考虑复杂的物理本质和发展过程，因此比以往模型更有利于工程应用。

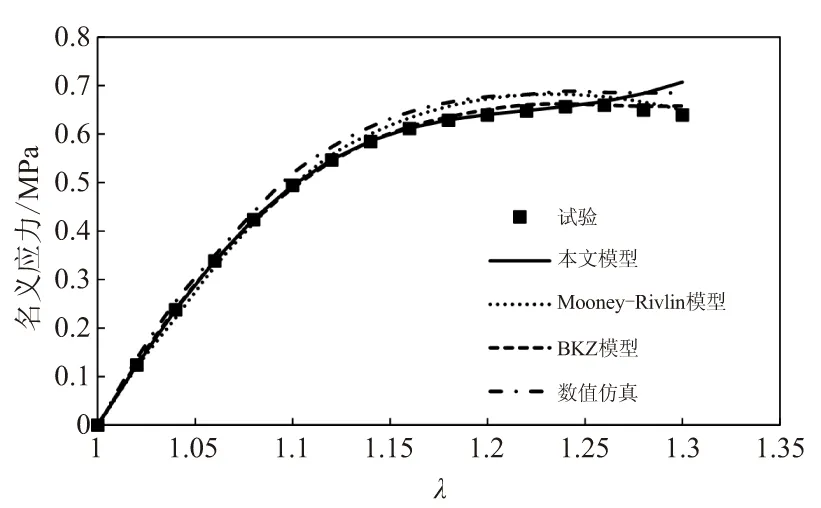
(a)2 mm/min

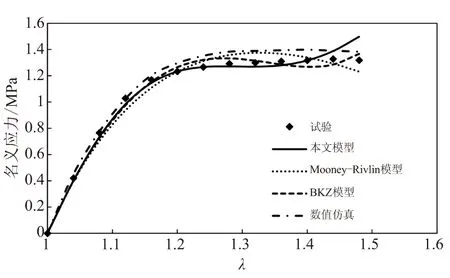
(b)2 000 mm/min

在较大变形时，模型误差较大的原因是从粘弹性应变能函数出发，研究推进剂的本构关系，并未考虑在较大变形下的损伤和破坏效应，单纯运用此模型，无法准确描述推进剂较大变形时的力学特性。描述推进剂大变形下的力学行为，需要计及损伤演化和破坏性能的更加普遍的理论模型。

以上同时验证了所建立应变能函数的有效性，由应变能函数表达式可得应变能密度与变形之间的关系，如图5所示。从图5可见，随变形量增大，推进剂的应变能密度呈非线性单调增长；同一变形条件下，应变率越高，推进剂的应变能密度越大。

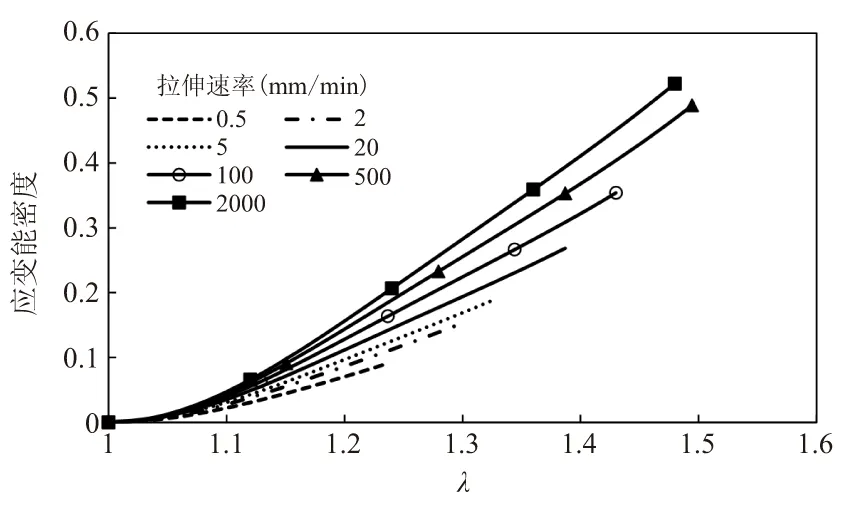
图5 推进剂应变能密度与变形的关系曲线Fig.5 Relationship between strain energy density and deformation of propellant

4 结论

(1)所提出的推进剂粘弹性应变能函数和非线性本构方程的一般形式，可较好反映材料在有限变形条件下的力学特性，选取幂函数作为回归方程，对不同应变率下的模型参数作一元非线性回归，得到了材料参数关于应变率的函数，由此建立的本构方程能够准确描述拉伸变形条件下的应力应变关系，且求解方法和方程形式较为简单，比以往更有利于工程应用。

(2)推进剂在不同拉伸速率下的材料参数不同，但呈规律性分布，拟合的参数函数反映了材料特性与应变率的关系呈现幂函数形式；推进剂应变能密度随变形的增大呈非线性单调增长，且在同一变形条件下，应变率越高，推进剂的应变能密度越大。

(3)模型对于复合推进剂应力应变行为的预测结果与试验结果吻合较好，但仍然存在不足之处，即较大变形时，模型的误差较大，且低应变率下的预测效果优于较高应变率下的预测效果。因此，所建模型尤其适用于表征低应变率拉伸条件下，材料在有限变形内的粘弹特性。

[1] 张永敬, 赵光辉, 阳建红, 等. HTPB复合固体推进剂非线性本构研究[J]. 推进技术, 2000, 21(4): 69-72.

[2] Leaderman H. Elastic and creep properties of filamentous materials and other high polymers[M]. Washington D C: Textile Foundation, 1943.

[3] Ward I M. Mechanical properties of solid polymers[M]. New York: Wiley, 2012.

[4] Shcapery R A. On the characterization of nonlinear viscoelastic materials[J]. Polymer Engineering and Science, 1969, 9(4): 295-310.

[5] Schapery R A. Correspondence principles and a generalized J intergral for large deformation and fracture analysis of viscoelastic media[J]. International Journal of Fracture, 1984, 25(3): 195-223.

[6] Schapery R A. Nonlinear viscoelastic and viscoplastic constitutive equations with growing damage[J]. International Journal of Solids and Structures,1999, 97(1-4): 33-66.

[7] Findley W N, Lai J S, Onaran K. Creep and relaxation of nonlinear viscoelastic materials[M]. Amsterdam: Noth-holland Publishing Company, 1976.

[8] Bernstein B, Kearsley E A, Zapas L J. A study of stress relaxation with finite strain[J]. Trans. Soc. Rheol.,1963, 7(1): 391-410.

[9] Gyoo D J, Sung K Y, Bong K K. A three-dimentional nonlinear viscoelastic constitutive model of solid propellant[J]. International Journal of Solids and Structures, 2000, 37(34): 4715-4732.

[10] 龚建良, 刘佩进, 李强. 基于能量守恒的HTPB推进剂非线性本构关系[J]. 含能材料, 2013, 21(3): 325-329.

[11] 邓凯, 阳建红, 陈飞, 等. HTPB复合固体推进剂本构方程[J]. 宇航学报, 2010, 31(7): 1815-1818.

[12] 彭威, 周建平, 任均国. 复合固体推进剂非线性粘弹本构方程的微观力学分析[J]. 固体火箭技术, 1999, 22(4): 23-25.

[13] Khajehsaeid H, Arghavani J, Naghdabadi R. A hyperelastic constitutive model for rubber-like materials[J]. European Journal of Mechanics A/Solids, 2013, 38: 144-151.

[14] Singh F, Katiyar V K, Singh B P. A new strain energy function to characterize apple and potato tissues[J]. Journal of Food Engineering, 2013, 118(2): 178-187.

[15] Garikipati K, Ktepe S G, Miehe C. Elastica-based strain energy functions for soft biological tissue[J]. Journal of the Mechanics and Physics of Solids, 2008, 56(4): 1693-1713.

[16] Hrapko M, Van Dommelen J A W, Peters G W M, et al. The mechanical behaviour of brain tissue: Large strain response and constitutive modelling[J]. Biorheology, 2006, 43(5): 623-636.

[17] Yang L M, Shim V P W, Lim C T. A visco-hyperelastic approah to modelling the constitutive behaviour of rubber[J]. International Journal of Impact Engineering, 2000, 24(6-7): 545-560.

[18] Hart-smith L J. Elasticity parameters for finite deformations of rubber-like materials[J]. The Journal of Applied Mathematics and Physics, 1966, 17(5): 608-626.

(编辑：刘红利)

Viscoelastic strain energy and nonlinear constitutive model for HTPB composite solid propellant

ZHANG Xiao，ZHENG Jian，PENG Wei，ZHANG Qian-tu

(Ordnance Engineering College，Shijiazhuang 050003，China)

To characterize the mechanical property of HTPB composite solid propellant under finite deformation condition, viscoelastic strain energy and nonlinear constitutive model were studied in this paper. The general forms of strain energy function(SEF) and nonlinear constitutive model were proposed, and the tensile test data were fitted by unitary nonlinear regression analysis. As a consequence, the material parametric function of strain rate was obtained, and on this basis the uniaxial tensile SEF and constitutive equation were established. The nominal stress curves at different strain rate were predicted, furthermore, they were compared with experimental results and prediction results of existing models. The results show the power function relationship between material parameters and strain rate, and the strain energy density proves to rise nonlinearly with strain, the higher the strain rate is, the larger the strain energy density will be at the same deformation. Moreover, the constitutive equation was demonstrated to be accurate on describing the tensile stress-strain relation of propellant, especially on representing the viscoelastic behavior at finite deformation and low strain rate.

HTPB propellant；strain energy；nonlinear regression；parametric function；constitutive equation；deformation

2014-09-01；

：2014-10-22。

张晓(1990—)，男，硕士，研究方向为固体推进剂力学性能。E-mail:erebuss@outlook.com

V512

A

1006-2793(2015)06-0827-06

10.7673/j.issn.1006-2793.2015.06.014