可压缩性修正湍流模型的高超声速飞行器流场模拟研究

刘海涌，刘朝阳，刘存良

(1.第二炮兵工程大学 动力工程系，西安 710025；2. 西北工业大学 动力与能源学院，西安 710072；3.第二炮兵驻航天科技集团第四研究院军事代表室，西安 710025)



可压缩性修正湍流模型的高超声速飞行器流场模拟研究

刘海涌1，2，刘朝阳3，刘存良2

(1.第二炮兵工程大学 动力工程系，西安 710025；2. 西北工业大学 动力与能源学院，西安 710072；3.第二炮兵驻航天科技集团第四研究院军事代表室，西安 710025)

采用经可压缩修正后的标准k-ε湍流模型对一类高超声速飞行器模型的气动特性进行了研究。计算中主要考虑了马赫数和飞行攻角的影响。计算结果表明，通过可压缩性修正，标准k-ε湍流模型能准确捕捉激波结构和复杂的压力变化规律；在激波系和预压缩面间构成的流动域内形成了高压均匀流动，实现了飞行器设计目标；在激波结构和激波发展趋势方面，计算结果和实验数据符合得很好，而两者在前体预压缩面上的压比值方面略有差异；经可压缩性修正后湍流模型的计算结果要明显优于原始湍流模型，可作为高超声速气动计算的有效方法。

高超声速飞行器；湍流模型；预压缩面；激波

0 引言

高超声速流场具有真实气体效应、磁流体干扰效应和力热结构耦合效应等多重流动特性，因而相关研究需扩展到分子动力学、电磁流体力学以及流固耦合等交叉学科领域，存在巨大挑战[1]。由于实验研究不能提供高超声速飞行包线全面细致的流动参数，数值模拟在其气动特性研究中发挥了重要作用。目前，RANS方法是应用最广，实际应用中通常对其控制方程加以修正，并对修正过程引入的新变量进行合理处理，实现方程封闭，从而减小计算量。k-ε模型是广泛应用的一种双方程湍流模型，能够准确地模拟大多数流动现象，且计算效率高，在内、外流场中得到广泛应用[2-4]。在高超声速研究方面，k-ε湍流模型的应用也广泛开展。Shyy等对k-ε模型的可压缩性修正进行了研究[5]，在湍动能的生成项、耗散项和输运项中引入了马赫数的影响，指出速度膨胀区的额外耗散必须引入可压缩修正。韩省思等在文献[6-9]中对标准k-ε模型的可压缩性修正进行了研究，这些研究考虑了Durbin和Chang实现性、Heinz湍流生成项和Sarkar可压缩性修正，结果表明即便是复杂的高超声速横向射流，修正模型都在分离区内取得了与实验结果相一致的计算结果。刘景源等对高超声速流动计算中的两方程湍流模型进行了对比研究[10]，研究结果表明在高超声速横掠流动问题中，双方程模型的可压缩性修正非常必要，经可压缩性修正后的计算结果与实验数据非常接近。耿云飞等对不同湍流模型在高超声速流动中的适用性进行了对比评估[11]，发现对于高超声速流动特别是大攻角流动，可压缩性修正不可或缺。Fulco采用涡点阵方法对升力面的下洗流进行了可压缩性修正[12]，引入可压缩性修正因子后的计算获得了精确结果。

综上所述，标准k-ε湍流模型还将在保留其独有特性(基本公式、计算稳定性和可控转变等)的基础上持续发展，但在高超声速技术领域，数值模拟中有必要对k-ε湍流模型进行修正。为了获取高超声速飞行器详细的流动参数，同时验证湍流模型在高超声速条件下的有效性，本文建立了一类高超声速飞行器模型，采用经可压缩性修正后的标准k-ε湍流模型开展数值模拟研究，并通过在类似模型上获得的实验数据对计算结果进行了验证。

1 湍流模型、可压缩性修正与近壁面处理

标准k-ε模型的输运方程可表达为

Gb-ρε-YM+Sk

(1)

(2)

式中k为湍动能；ε为湍动能耗散率；Gk和Gb分别为由当地速度梯度和浮力导致的湍动能生成项；YM为可压缩湍流中膨胀波动形成的耗散率；C1ε、C2ε、C3ε为常数，C1ε=1.44，C2ε=1.92，C3ε=0.09；σk和σε分别为与k和ε相对应的湍流普朗特数，σk=1.0，σε=1.3。

在标准k-ε模型的可压缩性修正中考虑了膨胀耗散修正、压力膨胀修正和激波不稳定修正三方面。其中膨胀耗散修正和压力膨胀修正参考文献[13]相关内容，可表达为

(3)

(4)

激波不稳定修正可表达为下述形式：

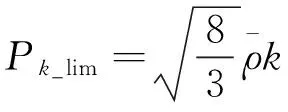
(5)

(6)

式中Pk为湍动能生成项，可压缩性修正在YM和UDF项中进行。

k-ε模型主要适用于湍流核心区，该区域距壁面较远。而在近壁面区域，流动参数变化梯度很大。因此，k-ε模型无法准确描述整个流动区域，需要在近壁面区域设定壁面函数。本文使用了增强型壁面函数，其主要方程可表达为

(7)

其中，

(8)

(9)

(10)

经过上述处理，整个流体域被划分为粘性底层和充分湍流区，可提高数值模拟精度，但也对近壁面区域的网格提出了更高要求。

2 计算模型与网格划分

设计并建立了类X-43A高超声速飞行器计算模型，其三维结构如图1所示，前体/进气口、内流通道和后体的二维结构如图2所示。飞行器前体由3段预压缩面构成。激波生成于预压缩面转角处，并在设计条件下向发动机入口汇集。δ1、δ2和δ3为流动转折角，β1、β2和β3为激波角。H0为进气道入口高度，L0为前缘至进气道唇口距离，l为外护罩延伸长度，Lforebody和Laftbody分别为前体和后体长度。

本文研究中未考虑飞行侧滑角的影响，因此流动沿机体长度方向呈对称形态。选用二维模型划分网格，由于模型的法向梯度远大于切向梯度，且壁面粘度效应要求必须在近壁面建立精细网格以捕捉粘性影响，因此在近壁面布置了15层矩形网格。为满足第一层网格距壁面无量纲距离y+≈1的要求，同时确保采用增强型壁面函数的k-ε模型能准确捕捉粘性底层信息，模型表面第一层网格距壁面距离不超过1×10-6m。在矩形网格外围，流动区域采用三角形网格并通过4条控制线对网格进行了局部加密。

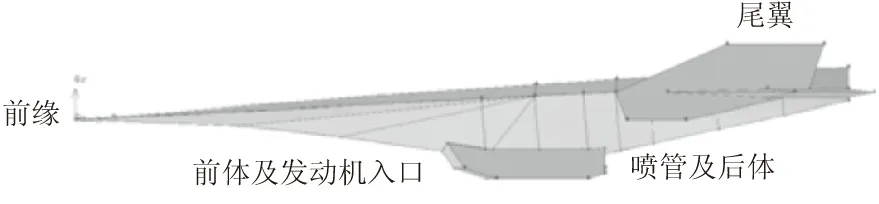
图1 高超声速飞行器三维模型Fig.1 Three-dimensional model of the hypersonic vehicle

图2 高超声速飞行器二维结构Fig.2 Configuration of the two-dimensional model of the hypersonic vehicle

模型的边界条件如图3、图4所示。计算区外边界为压力远场条件，飞行器壁面为绝热无滑移壁面。飞行器预设巡航高度25 km，所对应的计算条件：Ma=5、6、7、8，飞行攻角α=1.5°、3.5°，环境压力和温度分别为p0=2 600 Pa、T0=216.65 K。

图3 计算模型的网格与边界条件Fig.3 Grid and boundary conditions of the model

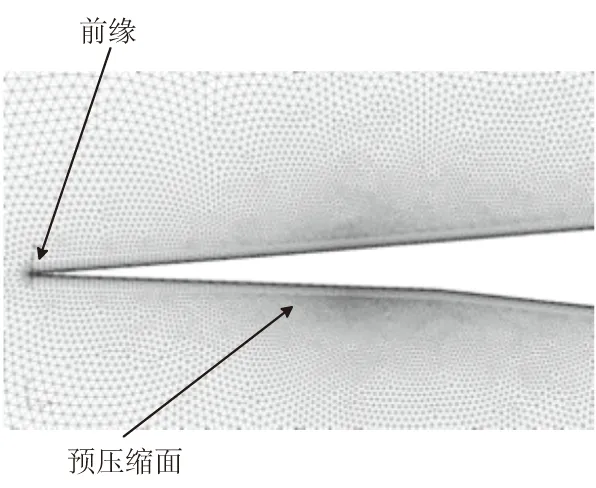
图4 飞行器表面附近网格设置Fig.4 Grid arrangement near the surface

网格质量对数值模拟计算具有重要影响，粗糙网格会带来较大的求解误差，而过于精细的网格则会耗费大量的计算资源与时间，因此在数值模拟中应尽量选用精确、稳定、经济的网格。本文选取了4种网格对模型进行了试算，其网格数量分别为约5×104、1×105、2×105和4×105。不同网格在给定位置的压比计算结果如图5所示。计算结果表明，当网格数量达到约2×105时，相关压力的计算结果已达到网格无关性要求，因此本文采用总数目约220 000的较为经济的网格开展计算。

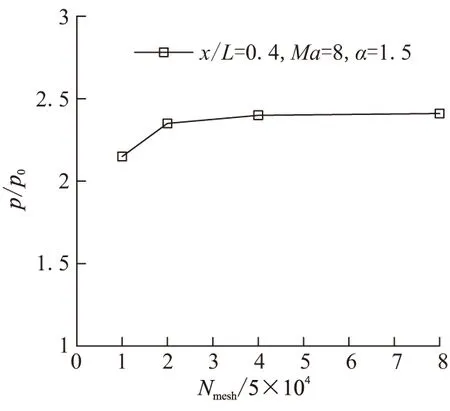
图5 计算结果的网格无关性检验Fig.5 Computational results for mesh- independent examination

3 结果与分析

3.1 计算结果的实验验证

张孙等建立了一种类X-43A高超声速飞行器模型，并对其气动性能和内部流动特性开展了实验研究[14]。与本文所研究的飞行器模型相比，两者的前体结构极为相似，因此文献[14]所获得的实验数据可作为本文计算结果的验证依据。图6即为文献[14]中的飞行器前体和发动机入口压力纹影图的实验结果。

由图6可看到，在前体预压缩面和自由流表面形成了一系列激波系，前体预压缩面的激波系在发动机入口附近交汇。与图8中的计算结果对比可看出，沿飞行器前体，无论是激波系的形态，还是压力变化趋势都极为一致。

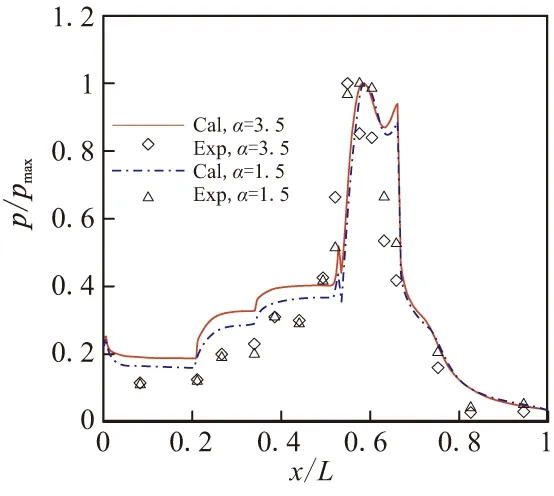
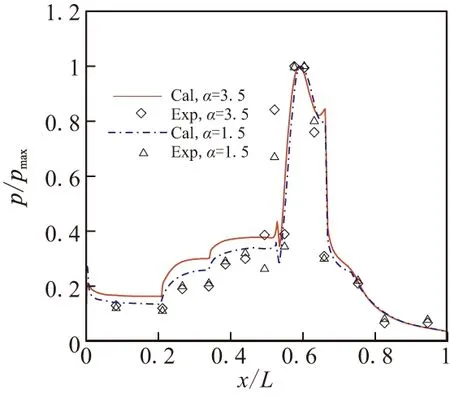
图7中将沿流动通道压力变化的实验结果与计算结果进行了对比，其中“EXP”表示实验数据，“CAL”表示计算结果。在前体区域，沿程压比的实验结果略低于计算结果，而在后体区域两者符合较好。在实验结果中，发动机入口位置存在明显的压力跃升，其波动范围要略高于计算结果。静压孔压力测量法在高超声速条件下会造成较大的压力损失，且在实验过程中前体预压缩面上存在压力泄露，使得前体预压缩面上压比的实验测量结果低于计算结果。总体上，计算结果与实验结果符合较好，经可压缩修正后的k-ε模型可为该类高超声速飞行器结构的气动计算提供可信数据。

(a) Ma=7,α=1.5° (b) Ma=8,α=1.5° (c) Ma=7,α=3.5° (d) Ma=8,α=3.5°

(a) Ma=7

(b) Ma=8

3.2 计算结果分析

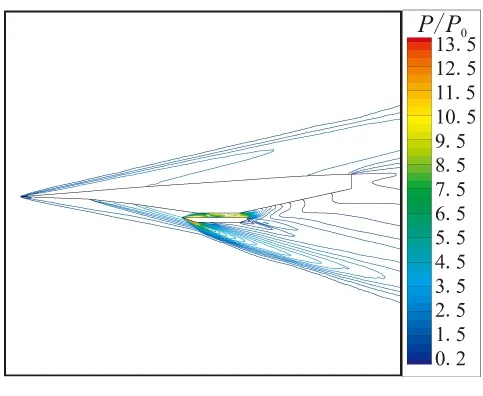
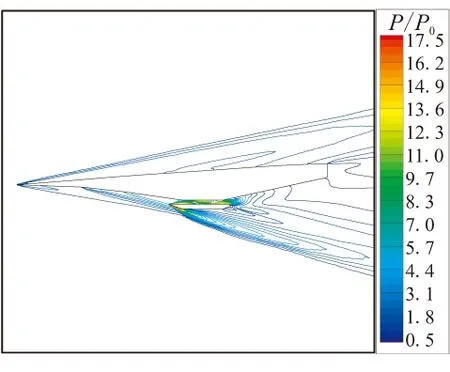
图8给出了计算条件为Ma=7、8和α=1.5°、3.5°时飞行器周围压力的计算结果。求解使用的湍流模型为经可压缩修正后的标准k-ε模型，压力计算结果用远场压力p0进行了无量纲化处理。从图8可看到，在3处预压缩面设计拐角处，形成了3条激波带。沿预压缩面长度方向，激波强度逐渐增强。在发动机内部也有激波存在，并使当地压力急剧升高。激波在由机体和发动机壁形成的通道内多次反射并在反射点附近形成局部高压区。气流在激波系和预压缩面间形成的流动空间内逐次流经激波系渐次增压，最后形成了高压的均匀流场。在发动机唇口位置也形成了一系列强激波系，该激波系将为飞行器带来较大阻力。在同一飞行攻角下，随着马赫数由7增加至8，压力的最大压缩比增加了约30%，而且激波倾角略有减小。在相同马赫数下，随着飞行攻角由1.5°增加至3.5°，预压缩面上的激波系强度增加，自由流表面激波系减弱，预压缩面上的激波系交汇点向发动机入口靠近。

(a) Ma=7，α=1.5°

(b) Ma=8,α=1.5°

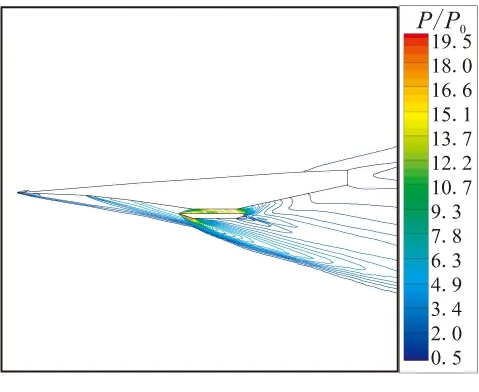
(c) Ma=7,α=3.5°

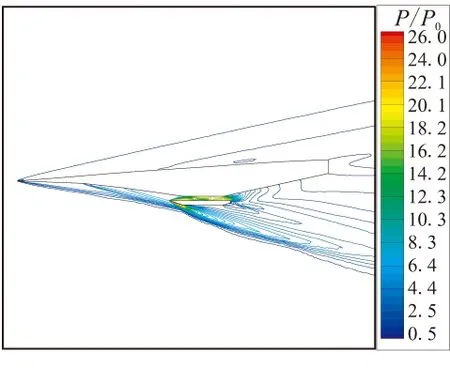
(d) Ma=8,α=3.5°

图9给出了不同马赫数和攻角下前体预压缩面、发动机内上表面和后体表面上的压力数据计算结果。所使用的湍流模型为经可压缩修正后的标准k-ε模型。由图9可看到，在前体预压缩面上存在3处清晰的压力跃升，跃升位置与预压缩面转角位置符合良好。在发动机入口位置，也存在一次压力跃升，这表明在该位置形成了强激波系。发动机内部的压力一直保持在较高水平，而在发动机尾部压力突然降低。发动机内部的激波反射使其内部压力形成双峰分布形态。随着马赫数的增加，前体预压缩面、发动机内上表面和后体表面上的压力提高，且发动机内部压力峰值形态发生变化，较高的压力峰值随马赫数的增加而不断向发动机入口靠近。这表明在发动机入口位置，激波强度不断提升。与马赫数相比，飞行攻角的增加同样会在总体上提升表面压力，但对压力峰值形态未产生明显影响。

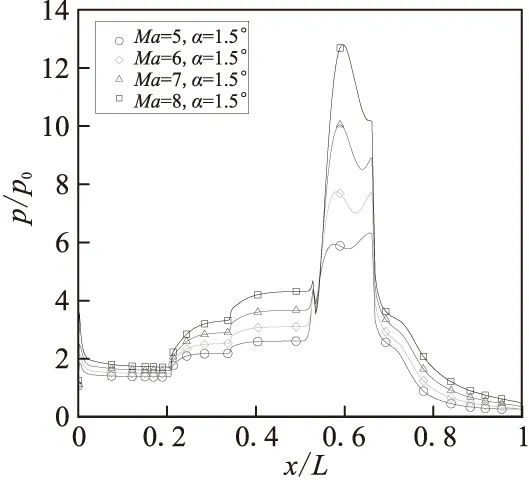
(a) Ma=5～8,α=1.5°

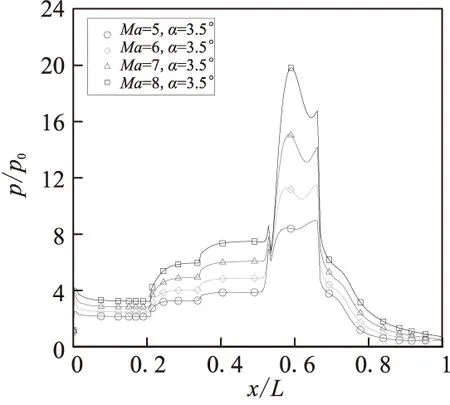
(b) Ma=5～8,α=3.5°

3.3 与未进行可压缩性修正标准k-ε模型计算结果的对比

图10给出了普通标准k-ε模型在Ma=7、8和α=1.5°、3.5°下飞行器周围的压力分布的计算结果。与经过可压缩性修正后的标准k-ε模型的计算结果相比，在未进行可压缩性修正的情况下，最大压比的计算结果要明显低于前者的计算值。在前体预压缩区域，普通标准k-ε模型未能捕捉到转折角处的激波系。图11给出了普通标准k-ε模型在不同飞行马赫数和攻角下，前体预压缩面、发动机内上表面和后体表面上的压力变化的计算结果。与图9中经过可压缩修正后的湍流模型的计算结果相比，普通模型未能捕捉到前缘处的压力变化；而在前体预压缩面上，压力呈线性升高趋势，未能捕捉到转折角处的压力跃升；在发动机出口位置，压力出现剧烈波动，未实现平滑过渡；在整个流动通道中，沿程压比值整体水平较低。

上述结果表明，在高超声速条件下，经过可压缩性修正后的标准k-ε模型能更为准确的反映压力变化，捕捉激波能力增强，计算精度和稳定性提高，能够提供更为准确的计算结果。

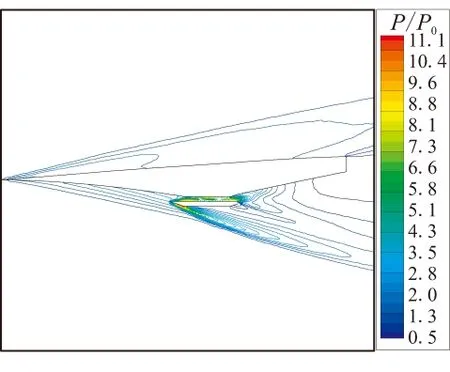
(a) Ma=7，α=1.5°

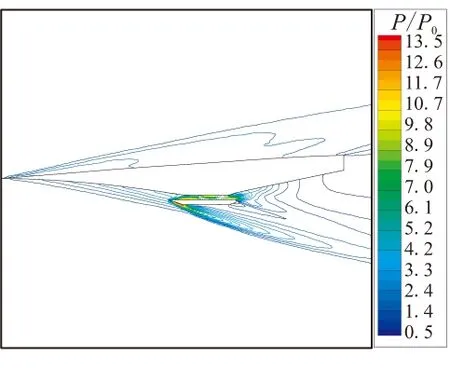
(b) Ma=8,α=1.5°

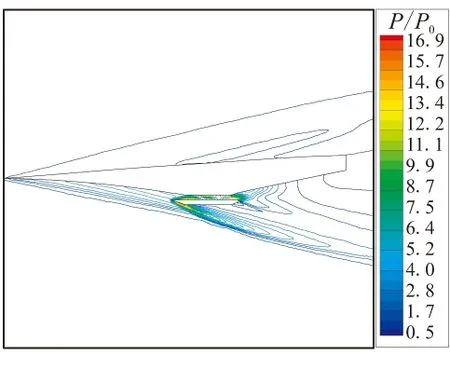
(c) Ma=8,α=3.5°

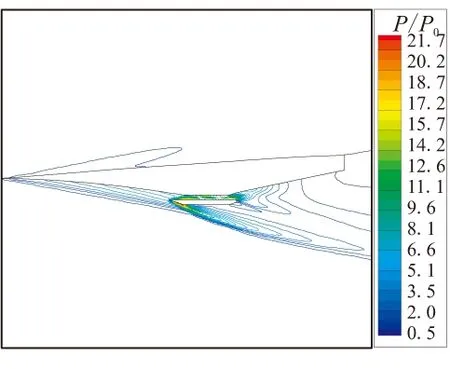
(d) Ma=8,α=3.5°

(a) Ma=5～8,α=1.5°

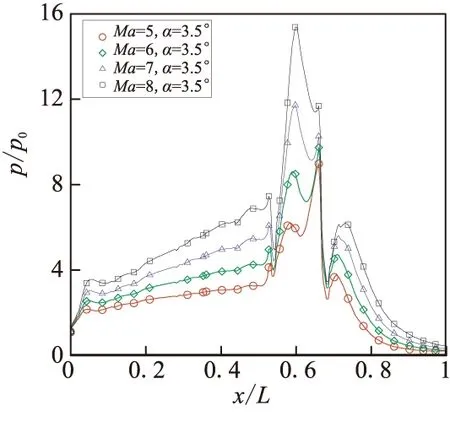
(b) Ma=5～8,α=3.5°

4 结论

(1)计算结果表明飞行器模型实现了初始设计目标。在激波系和预压缩面间构成的流动域内形成了高压均匀流动，为飞行器提供了很高升力。在发动机内部，流动减速并形成高压环境，有利于发动机点火和稳定燃烧。经可压缩性修正后，标准k-ε模型能准确捕捉激波结构和压力变化特性，在前体预压缩面上压力表现出阶梯跃升，在发动机内部压力跃升并保持较高压力水平。

(2)实验模型中获取的压力纹影图提供了有价值的激波结构和压力变化趋势信息。在激波结构方面，实验数据与计算结果良好符合。但在前体预压缩面上的压力变化方面，沿程压比的计算结果高于实验结果，实验中测量方法造成的压力损失是造成上述差别的主要原因。总体上，计算结果与实验结果较好符合，经可压缩修正后的k-ε模型可作为该类高超声速飞行器结构气动计算的有效方法。

[1] 王江峰,伍贻兆,季卫栋,等.高超声速复杂气动问题数值方法研究进展[J].航空学报,2015,36(1)：159-175.

[2] 谢春艳,张敬秋,王洋.改进型k-ε湍流模型在三维侧喷流数值仿真中的应用[J].导弹与航天运载技术,2014,330(1):56-60.

[3] 刘薇,宋国萍,褚双磊,韩博.基于ANSYS FLUENT的近场翼尖涡数值模拟与分析[J].飞行力学,2015,33(2):16-21.

[4] 王乐,宋卫东,杨晓霖.基于可压缩修正k-ε模型的弹丸气动计算[J].弹箭与制导学报,2013(1):149-151.

[5] Shyy W,Krishnamurty V S.Compressibility effects in modeling complex turbulent flows[J].Aerospace Science,1997,33:587-645.

[6] 韩省思,叶桃红,朱雯明,等.一个新的可压缩性修正的k-ε模型[J].空气动力学学报,2009,27(6):677-682.

[7] 韩省思,叶桃红,朱旻明,等.k-ε湍流模型可压缩性修正在超音速混合层中的应用研究[J].工程热物理学报,2007,28(6):1053-1055.

[8] 韩省思,刘亮,叶桃红,等.三种湍流对Scramjet燃烧室冷态流场的数值模拟[J].中国科学技术大学学报,2009,39(3):321-325.

[9] 韩省思,叶桃红,朱旻明,等.激波不稳定性效应的k-ε可压缩修正湍流模型[J].科学通报,2008,53(22);2722-2729.

[10] 刘景源,李椿萱.高超声速二方程湍流模型的数值模拟对比[J].北京航空航天大学学报,2007,33(10):1131-1135.

[11] 耿云飞,阎超,徐晶磊,等.高超声速流动湍流模式评估[J].北京航空航天大学学报,2011,37(8):907-911.

[12] Fulco V,Roelof V.A new compressibility correction method to predict aerodynamic interaction between lifting surfaces[R].AIAA 2013-4299.

[13] Sarkar S,Erlebacher G,Hussaini M Y,et al.The analysis and modeling of dilatational terms in compressible turbulence[J].Journal of Fluid Mechanics,1991,227:473-493.

[14] 张孙.类X-43A高超声速飞行器气动力特性及其全流道流动特征的研究[D].南京：南京航空航天大学,2007.

(编辑：吕耀辉)

Research on the application of a turbulence models with compressibility effects correction for a hypersonic vehicle

LIU Hai-yong1，2，LIU Chao-yang3，LIU Cun-liang2

(1.School of Engine and Energy，Second Artillery Engineering Univ.，Xi'an 710025，China；2.School of Power and Energy，Northwestern Polytechnical Univ.，Xi'an 710072，China；3.Military Representative Department of the 2nd Artillery Force Stationed in the 4th Research Academy of CASC，Xi'an 710025，China)

A series of numerical analyses have been performed to investigate the flow characteristics of a hypersonic vehicle model. Flow fields corresponding to the Mach number and attack angle were analyzed by solving the Reynolds averaged Navier-stokes equations with the standk-εturbulence model in which the compressibility effects were considered. With the correction of compressibility effects，the standardk-εturbulence model can capture delicate shock wave structures and complex pressure variation characteristics,and their calculation results are in highly agreement. The calculated shock wave structures and pressure variation tendency agree well with experimental data，except for some differences in the variation of the static pressure on the pre-compressed surface. Compared with the originalk-εturbulence model,the improved model with compressibility effects correction obtains more accurate data,implying the validity and effectiveness of the numerical approach for analyzing relevant flow field.

hypersonic vehicle；turbulence model；pre-compressed surface；shock wave

2015-01-03；

：2015-05-17。

国家自然科学基金(51206180)；陕西省自然科学基金(2014JQ7276)。

刘海涌(1981—)，男，博士后，主要从事飞行器及发动机高温部件热防护技术研究。E-mail:helian_xicheng@163.com

V430

A

1006-2793(2015)06-0770-06

10.7673/j.issn.1006-2793.2015.06.004