扭曲尾翼弹箭的马格努斯数值研究

赵博博，刘荣忠，郭 锐，张 迪，袁 军，陈 亮

(1.南京理工大学 机械工程学院，南京 210094；2.中国人民解放军73917部队，南京 290014；3.中国人民解放军陆军军官学院，合肥 230000)



扭曲尾翼弹箭的马格努斯数值研究

赵博博1, 2，刘荣忠1，郭 锐1，张 迪3，袁 军1，陈 亮1

(1.南京理工大学 机械工程学院，南京 210094；2.中国人民解放军73917部队，南京 290014；3.中国人民解放军陆军军官学院，合肥 230000)

为提升掠飞攻顶弹箭较高转速下的飞行稳定性，运用数值计算方法研究了弹体-扭曲尾翼组合体在飞行过程中的马格努斯效应气动机理，并应用标准尾翼弹(BFM)模型的实验数据对数值方法进行了验证。分别研究了带有平板尾翼和扭曲尾翼弹体模型的马格努斯力和力矩随攻角的变化规律，并针对弹体弹翼组合体产生马格努斯效应的机理深入分析。结果表明，扭曲尾翼可有效改善翼面的压力分布，并降低弹体对翼面马格努斯效应的干扰，在大攻角时其表现更胜一筹；弹体所受马格努斯力较大，主要集中在受到涡对称畸变的尾锥部；尾翼主要由于弹体干扰以及几何外形的影响马格努斯力集中在尾部，两者产生的马格努斯力矩数值相差不大，但方向相反。

流体力学；扭曲尾翼；旋转尾翼弹丸；马格努斯效应；数值仿真

0 引言

掠飞攻顶末敏弹是一种采用非直瞄方式向装甲目标方位发射的新型末敏弹，应用旋转的弹体作为扫描平台，弹丸一边飞行一边高速旋转，敏感器对前侧方进行探测扫描，扫描区域为柱形区，一旦探测到目标，即按一定的决策规则起爆MEFP战斗部，所形成的多枚弹丸从装甲目标上方击毁目标[1-2]。旋转的弹体不仅可有效降低由质量偏心、尾翼加工误差、推力偏心等因素的引起的弹丸散布，还作为敏感探测器的扫描平台[3]。普通尾翼弹转速仅仅为30 r/s以内，掠飞攻顶末敏弹则要求转速为其2～3倍[4]。但随着转速的增加，旋转产生的马格努斯效应不再可忽略，将引起弹丸攻角增加，甚至破坏弹丸静稳定性，导致飞行失稳[5]，扭曲尾翼作为一种新型高转速尾翼弹结构，具有增加转速、降低阻力的优势，对其开展研究也未见于报道。由此可见，研究马格努斯力与力矩对较高转速要求的掠飞末敏弹具有重要意义。

旋转弹马格努斯效应是由弹体表面附面层内复杂三维流动产生，引起弹体相反的两面压力不对称[6]，其不仅与弹体转速和攻角相关，还与弹丸质心、弹体外形、马赫数、雷诺数等有关；尾翼稳定弹在零转速时，即存在马格努斯效应，这是由尾翼的差动配置与弹体之间相互影响产生[7]；过去对马格努斯效应的研究主要通过实验的方法，文献[8-9]通过风洞实验方法研究了标准尾翼模型(BFM)在超音速、跨音速下的马格努斯力与力矩，指出尾翼弹马格努斯力具有非线性的特性，在跨音速时受尾翼影响较大；文献[10]则研究了旋转弹在不同马赫数与转速下的马格努斯效应，但风洞实验方法对设备要求非常高、周期长、花费昂贵；数值仿真在附面层的畸变，弹体受力分析上具有直观、清晰的优势，但由于马格努斯力相对较小，数值仿真较难实现[11-12]；文献[13]对BFM模型进行数值仿真，并与美国阿诺德实验中心风洞数据进行对比，成功实现了平均雷诺下的N-S方程对大攻角条件下尾翼弹进行数值模拟；文献[14]通过数值和实验相对比的方法，验证了数值方法对旋转弹模拟的精确度；文献[15-16]也对马格努斯效应开展了一定研究。

将掠飞攻顶末敏弹简化为带有尾杆结构的扭曲尾翼弹丸，由于尾杆直径远小于弹体直径，导致风洞实验特别是缩比实验受到尾杆直径的限制而难以实现。所以，对此类结构的尾翼弹实验较少。本文通过数值仿真的方法，采用滑移网格技术，先对BFM模型数值模拟，与实验数据进行对比，进行算法验证，然后计算了扭曲尾翼弹丸的马格努斯力与力矩，并深入分析，对新型尾翼结构弹丸设计具有较大参考意义。

1 数值方法

数值计算方法具有清晰、直观的优势，能从机理上解释马格努斯效应产生的原因。

1.1 掠飞末敏弹模型

模型为带有尾杆结构的扭曲尾翼弹丸，如图1所示。尾翼弹丸总长为6.5D，头部长为1.5D，头部为圆弧形母线，半径为3.2D，圆柱部长2.4D，尾锥锥角为45°，尾杆直径为0.4D、长度为2.05D，尾翼翼展为2.72D，翼弦为0.28D，厚度为0.024D。弹体转动方向为从弹尾向弹头方向看为顺时针旋转。

图1 “十字形”布局扭曲尾翼弹丸结构图Fig.1 The cruciform layout twist fin projectile model

图2中，扭曲尾翼为一种沿翼展均匀扭曲的尾翼，在翼根处安装攻角较小，沿翼展安装攻角均匀增大。引入扭曲率K(y)和平均攻角εm表示尾翼的几何特征，定义如下：扭曲率K(y)表征沿翼展延伸方向尾翼面的扭曲程度，将安装角δ(y)对翼展y求偏导，得到扭曲率为

K(y)=∂δ(y)/∂y

(2)

平均攻角εm的正弦值等于扭曲尾翼在yoz平面上的投影面积与尾翼侧表面积的比值，是扭曲尾翼与斜置平板尾翼相对比的重要参考量，即

εm=arcsin(S1/Sw)

(3)

式中S1为尾翼面在垂直于弹轴平面上的投影面积；Sw为翼面的侧表面积。

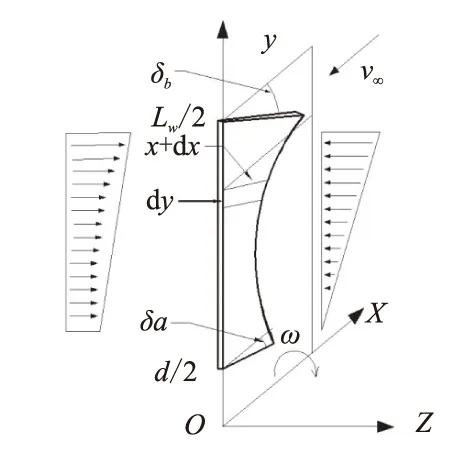
图2 扭曲尾翼几何模型Fig.2 The geometric model of twisted fin

采用笛卡尔右手坐标系，坐标原点在弹尾中心，x轴正向从弹头部指向弹尾部，y轴指向上方，z轴垂直于xoy平面，指向外方向。可知，当攻角向上，尾翼弹丸顺时针旋转时，根据马格努斯力的经典解释，旋转弹的马格努斯力指向z轴正向。

取两个模型计算：第一个模型为特殊的扭曲尾翼，即扭曲率为0的平板尾翼，由平板尾翼偏置13°，记为F1；第二个模型为翼根处攻角小，翼梢处攻角大，沿翼展方向扭曲率为0.11°/mm的扭曲尾翼，扭曲尾翼的平均攻角仍为13°，记为F2。

1.2 网格划分及边界条件

滑移网格技术是一种易实现的动网格技术，具有计算速度快、占用内存少、精度高等优点。将流场划分为内外2个具有交接面的区域，滑移网格技术通过设置内外2个区域的不同转速，实现不同域内网格的绕轴转动。马格努斯效应主要是由边界层的复杂三维流动引起。所以，网格的质量是影响求解结果的关键因素。如图3(a)所示，将流场划分为内外两个区域，采用圆柱形流场区域，以防止激波溢出。为减少网格数目，采取内部流场区域网格较外部区域密，交接面上节点不用对齐。为了得到准确的翼面气动力特性、以及边界层的复杂流动，使用O型拓扑结构对弹体周围加密。如图3(b)、(c)所示，壁面第一层网格的厚度采用0.002 mm，以满足y+<1，随着网格向外延伸，控制网格厚度增长率小于1.3，以保证网格的均匀增长。

(a)总体网格结构 (b)弹头部网格结构 (c)尾翼部网格结构

湍流模型采用具有更高可信度和精度的剪切压力运输(SST)k-ω模型，该模型结合了k-ε模型与k-ω模型的优点，将混合功能和双模型叠加在一起，此模型避免了应用壁面函数时对网格的y+要求较低的近似方法，而是直接对附面层内进行模拟，对网格要求很高。

采用有限体积法对空间进行离散，采取基于密度的隐式耦合算法，时间项采用稳态方法来计算模型在给定状态下的气动特性，采用迎风型矢通量分裂格式(AUSM+)计算对流和流体压力，AUSM+ 格式兼有Roe格式的间断高分辨率和VanLeer格式的计算效率，而且克服了二者的缺点。

远场入口边界采用压力远场，设置来流值，远场周向边界采用自由流条件，外部区域不转动，内部区域采用网格移动条件，设置转速。弹体采用壁面边界条件，边界采用无滑移边界条件，壁面采用运动方式，运动为旋转方法，旋转轴为弹轴，壁面与内部运动区相关联。

2 网格收敛性及算法验证

采用标准尾翼弹模型(BFM)进行算法验证[9]，几十年来此模型在国外被作为参考模型，已经积累了大量风洞实验数据，是较成熟的研究弹型，其尺寸为模型尺寸为弹身直径D=45 mm，弹长为10D，锥形头部角度20°，翼展3D，弦长为D，翼宽0.08D，质心距离弹头部6.1D，尾翼偏置角度为3°，求解不同条件下的马格努斯力及力矩，进行算法的有效性验证。计算中，分别采取130万、280万、430万的网格数目进行求解，验证网格的收敛性。结果表明，在网格数目为280万时，满足精度要求。

图4 BFM模型仿真结果对比Fig.4 The simulation comparison with experimental result

将仿真数据与风洞实验数据相比较[10]。图4为在2种条件下，BFM马格努斯力数值仿真值与实验值对比结果。可知，数值仿真结果与实验数据相吻合。其中，对于Ma=1.1、ω*=0.025时，吻合较好。对于Ma=2.5、转速较低为ω*=0.025时，误差较大，最大误差为25%，但基本规律相吻合。可得CFD方法在求解小攻角，高转速的情况下有较高的精确度，验证了算法的正确性。

3 计算结果分析

计算条件：Ma=1.5，总温T0=300 K，攻角α=0°～12°，无量纲转速ω*=ωr/v∞=0.122(其中ω为弹丸转速，r为弹体最大半径，v∞为来流速度)，采用气体为理想气体。分别计算模型F1，F2，模型F1尾翼为平板尾翼，模型F2尾翼为相同平均偏置角下的扭曲尾翼。

3.1 整体结果分析

图5为模型尾翼、弹体及组合体马格努斯力系数随攻角的变化曲线。对于模型F1与F2，由于弹体外形及飞行条件完全一样，且在尾翼后端受尾翼干扰的弹体区域较小。所以，认为2种模型弹体的马格努斯效应完全一致。模型弹体受到z轴正向的马格努斯力，随着攻角增加，当攻角大于一定值后变化不大；模型F1、F2尾翼上马格努斯力比弹体小得多，与弹体反向指向z轴负向，且F1的尾翼随着攻角增大马格努斯力出现换向，F2的尾翼上的力随攻角一直增加；组合体的马格努斯力为小攻角时模型F1大于F2 ，较大攻角时相反，组合体总体小于单独弹体的马格努斯力。

图6为模型尾翼、弹体及组合体的马格努斯力矩变化曲线。由图6可知，尾翼的马格努斯力矩和弹体数值差别不大，但与弹体呈反向；在小攻角时，模型F2的马格努斯力矩略大于模型F1，在大攻角时，远小于F1，这说明扭曲尾翼能有效改善模型的马格努斯力矩。这是由于F2尾翼上的马格努斯力矩随攻角先增大、后减小，但减小幅度不大，始终与弹体保持反向；F1尾翼的马格努斯力矩在较大攻角换向，提供与弹体马格努斯力矩方向一致的力，导致组合体力矩增加。

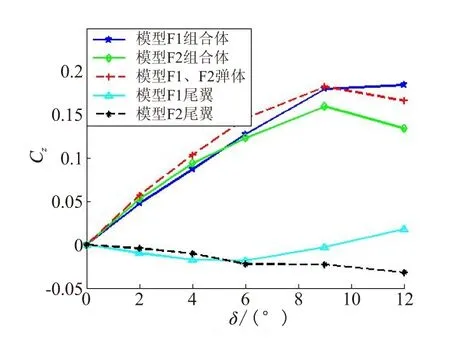
图5 模型F1、F2的马格努斯力系数的变化曲线Fig.5 Change of Magnus force coefficient of model F1,F2

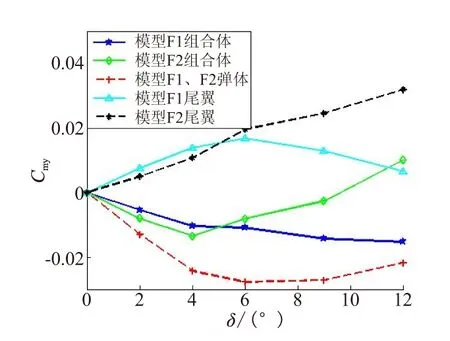
图6 模型F1、F2的马格努斯力矩变化曲线Fig.6 Change of Magnus moment coefficient of model F1,F2

3.2 尾翼马格努斯效应分析

已知平板尾翼的马格努斯力随着攻角的增加呈现反向的趋势，而扭曲尾翼马格努斯力随着攻角的增大方向不变。针对尾翼上马格努斯效应产生机理单独分析。

图7为翼面中点处的赤道面与上下翼面的交线上的压力差沿y轴的分布，D为弹体直径。图9中，左边为尾翼3，右端为尾翼1。由图7、图8知，对于F1的尾翼1翼根处零攻角时产生z轴正向的力，尾翼3翼根处产生z轴负向力，有攻角时打破平衡，尾翼3翼根上压强更高，提供z轴正向力；同样，在模型F1的尾翼1、3的翼梢处，由于攻角引起的压力变化，使尾翼3压强高受到z轴正向力，两者相互抵消，导致模型F1的马格努斯力随着攻角的变化先增大，后反向。对于模型F2的尾翼3，由于扭曲翼面上实际攻角均匀，平衡转速下几乎为零，在有攻角δ时，弹体对尾翼3翼面的干扰带来的压力变化并不影响翼面压力分布；而模型F2的尾翼1在翼根处受到尾杆的干扰，攻角越大产生的涡越强烈，对尾翼1翼根处产生越大的z轴负向力。所以，模型F2的尾翼马格努斯力随着攻角增加而增加。可见，尾翼的马格努斯力产生的原因主要是因为弹体对尾翼的干扰，有攻角时，扭曲尾翼同样改善压力随翼展的分布。

图7 δ=9°时尾翼1、3翼面z方向压强分布Fig.7 z direction component of pressure at wing 1,3

尾翼上马格努斯力矩一部分由尾翼1、3的马格努斯力产生，另一部分源于差动配置的尾翼2、4翼面上压强在x轴的分量。

图8为翼面中点处赤道面与尾翼上下翼面的交线上的压力差及其在x轴(对安装角取正弦)上投影沿z轴的分布。右边为尾翼4，左边为尾翼2，D为弹体直径。尾翼2、4的压强主要源于安装角、弹体攻角、以及转速引起的附加攻角共同作用。模型F1为平板尾翼，相比较于模型F2的扭曲尾翼，则翼根处安装角较大，翼梢处安装角小。所以，模型F1尾翼4在翼根处压力大于模型F2，在翼梢处小于模型F2；模型F1的尾翼2在翼根处提供较大的向下的安装角。所以，在翼根处压力较小，在翼梢处的压强较大。对比可知，尾翼4上由于弹体攻角与安装角同向，导致尾翼4压力分布最不均匀，扭曲尾翼同样改善翼面上的压力分布。

图8 δ=9°时尾翼2、4翼面压强及翼面x方向压强分布Fig.8 Pressure distribution and x direction component on the surface of the wing 2,4

由于图8中尾翼2、4压力差在x轴上分量方向相反，所以产生y轴正向的力矩。模型F2的尾翼2在翼梢处压力虽然不大，但此处尾翼安装角较大，仍存在较大的x轴正向分力，尾翼4同样存在较大x轴负向分力。所以，模型F2尾翼的马格努斯力矩大于模型F1，主要是由于扭曲尾翼翼梢处安装角较大而导致；模型F2尾翼的马格努斯力矩与弹体相反，达到降低组合体的马格努斯力矩的效果。

3.3 弹体马格努斯效应分析

弹体的马格努斯效应同样是影响弹丸马格努斯效应的重要因素。单独弹体的马格努斯效应主要由于空气的粘性作用产生，边界层位移厚度的非对称畸变、边界层转捩非对称畸变、径向压力梯度的非对称畸变、周向切应力的非对称畸变和体涡的非对称畸变是马格努斯效应产生的重要原因[6]。

下面对主要产生弹体马格努斯效应的主要因素进行分析。

3.3.1 弹体流场曲线

弹体的马格努斯效应同样是影响弹丸马格努斯效应的重要因素。图9为弹丸周围流场的流线图，在小攻角时，流体沿头部、圆柱部的壁面流动，由层流逐渐转化为湍流，在尾锥部形成明显的涡，此时涡仍较对称；而大攻角时，流体在背风面涡会脱离附面层，特别是尾锥部的涡明显呈现非对称。可见，在不同攻角时，导致马格努斯效应的机理不同。

3.3.2 弹体圆柱部

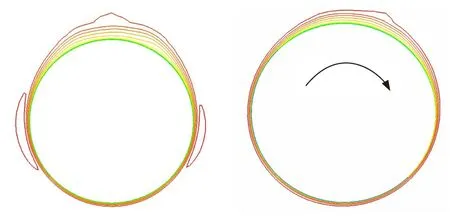
图10为Ma=1.5旋转弹丸和无旋弹丸在圆柱部(x=-3.5D)赤道面弹体周围速度等值线，弹体部不旋转时，边界层相对于弹体攻角平面对称，且下部等值线较密，上部稀疏；当弹体旋转后左侧等值线变薄，速度增加，由于超音速下速度大压强小，所以左侧压强减；右侧等值线变稀疏，说明速度减小，压强增大，在弹体圆柱部产生z轴正向的力。这是因为在攻角的条件下，弹体受到由下向上的横流，由于气体本身具有粘性，当弹体旋转时带动周围流场沿弹体旋转产生环流。由于弹丸左侧环流速度与横流速度相同，所以气流速度增大，且弹体附面层变薄； 右侧环流速度与横流速度相反，流速降低，则附面层变厚，压强增大，即产生z轴正向的侧向力。

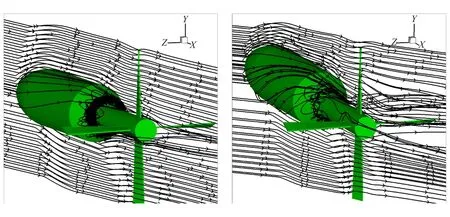
(a)δ=2° (b)δ=9°

(a)ω*=0 (b)ω*=0.122

图11为Ma=1.5、δ=9°时，无旋弹丸和旋转弹丸在圆柱部(x=-4.5D)与赤道面交线的压力分布曲线。在弹体不旋转时两侧压力对称，且迎风面压力远大于背风面压力，此时弹丸受到强烈的正升力；旋转弹丸周向压力分布不再对称，主要表现为在弹丸在背风面右侧的压力大于左侧的压力，使弹丸受到z轴正向的压力。这主要由于边界层位移厚度的非对称畸变、边界层转捩非对称畸变引起；在迎风面左侧压力大于右侧，弹丸受到z轴负向的压力，主要由于周向切应力的非对称畸变以及气体离心力的作用，但弹丸总体受到z轴正向的压力。

3.3.3 尾锥部马格努斯效应

图12为流场在尾锥部(x=-2.3D)的赤道面内流线及密度云图。可知，流场在尾锥部流动非常复杂，但主要受到体涡的非对称畸变及边界层的畸变的影响。图12(a)为旋转弹体在攻角为零时，尾锥部的流线及密度云图。此时，由于没有攻角，弹体附面层内有均匀环流，带动周围流场均匀旋转，由于流场在尾锥部受到膨胀波的影响，速度增加密度减小，使密度呈现梯度变化，密度也是均匀轴对称，此时没有侧向力。图12(b)为弹丸在攻角为9°不旋转时的密度云图。此时，迎风面密度高，背风面密度低，云图不在是轴对称，而是相对于攻角平面对称，仍没有侧向力，流线不再是均匀的环流，呈现面对称的流场，同时在弹体背风面产生两个对称的涡，这是因为流线脱体，在背风面与附面层分离。图12(c)为旋转弹丸在攻角为9°时的密度云图。此时，旋转弹体背风面内的流动分离产生的涡已经严重非对称。其中，左侧的涡由于旋转向弹体靠近，已依附在弹体上，而右侧的涡顺时针方向移动，远离弹体。由于涡的中心压强较低，外围压强高，所以左侧涡依附在弹体上形成低压区，右侧的涡低压区远离弹体，弹体表面为高压区，产生z轴正向力。

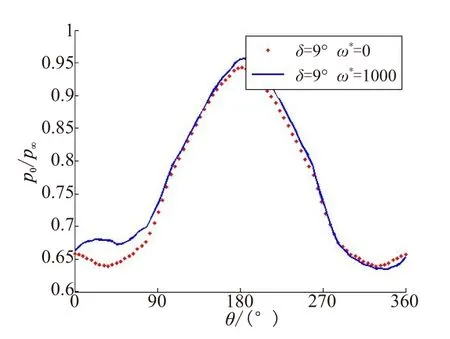
图11 弹体在圆柱部(x=-4.5D)处周向压力分布Fig.11 Computed Circumferential surface pressure distribution δ=9°, x=-4.5D

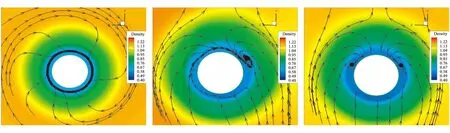
(a)δ=0°,ω*=0.122 (b)δ=9°,ω*=0 (c)δ=9°,ω*=0.122

4 结论

(1)尾翼上的马格努斯力主要由弹体存在攻角时，弹体对气流的干扰，流过尾翼的上下翼片所引起，导致上下翼片压力改变。平板尾翼翼面上翼根、翼梢受力不均衡，更容易受压力改变的影响，马格努斯力变化剧烈；扭曲尾翼能有效改善翼面上的实际攻角，从而改善压力分布，增强了翼面的抗干扰性，马格努斯力变化规律，在大攻角时表现更胜一筹。

(2)弹体整体受到z轴正向的马格努斯力，圆柱部由于主要为层流的影响、尾杆处虽然为湍流，但直径较小，马格努斯效力并不大；尾锥处有较强的涡畸变产生，此处马格努斯力最大，但由于此处靠近弹丸质心，弹体整体的马格努斯力矩并不大，这为掠飞攻顶末敏弹气动优化提供依据。尾翼处远离质心，受到z轴负向的马格努斯力，虽然作用在尾翼上马格努斯力并不大，但由于力臂长，所以尾翼马格努斯力矩和弹体上数值相似，方向相反。

(3)通过数值仿真的方法，对弹体弹翼组合体的马格努斯效应产生机理，指出了弹体、弹翼的马格努斯效应主要影响因素并进行分析，这对降低掠飞攻顶末敏弹的马格努斯效应及弹丸气动优化具有重要意义。

[1] 杨绍卿. 灵巧弹药工程[M]. 北京: 国防工业出版社, 2010.

[2] Megson, Thomas H.Aircraft structures for engineering stud-ents[M]. Access Online via Elsevier, 2012.

[3] 胡志鹏, 刘荣忠, 郭锐. 两种典型尾翼形状对无伞末敏弹气动特性的影响[J]. 南京理工大学学报, 2012, 36(5).

[4] 赵博博, 刘荣忠, 郭锐. 扭曲尾翼飞行器气动特性数值研究[J].国防科技大学学报,2014(3).

[5] Oh S Y, Kim S C, Lee D K, et al. Magnus and spin-damping measurements of a spinning projectile using design of experiments[J]. Journal of Spacecraft and Rockets, 2010, 47(6): 974-980.

[6] Schlichting H. Boundary-layer theory[M]. McGraw-hill Bo-ok Company, 1979.

[7] Morote J, Liao G. Prediction of nonlinear rolling and magnus coefficients of cruciform-finned missiles[J]. Journal of Aircraft, 2010, 47(4): 1413-1425.

[8] Arnan Seginer, Izhak Rosenwasser. Magnus effects on spinning transonic missiles[R]. AIAA 83-246.

[9] Jenke L M. Experimental roll-damping magnus, and static stability characteristics of two slender missile configurations at high angles of attack (0 to 90 deg)and Mach numbers 0.2 through 2.5[R]. AEDC-TR 76-58.

[10] Sturek W B, Dwyer H A, Kayser L D. Computations of magnus effects for a yawed, spinning body of revolution[J]. AIAA Journal, 1978, 16(7): 687-692.

[11] Sahu J. Numerical computations of dynamic derivatives of a finned projectile using a time accurate CFD method[R]. AIAA 2007.

[12] James Despirito. CFD prediction of magnus effect in subsonic to supersonic flight[J]. Army Research Laboratory, ARL-TR-4929, 2009.

[13] Bhagwandin V, Sahu J. Numerical prediction of dynamic stability derivatives for finned projectiles[C]//Ballistics 2013: 27th International Symposium on Ballistics. DEStech Publications, Inc, 2013: 186.

[14] Klatt D, Hruschka R, Leopold F. Numerical and experimental investigation of the magnus effect in supersonic Flows[R]. AIAA 2012-3230.

[15] 薛帮猛，杨永. 旋转弹丸马格努斯力数值计算[J]. 弹箭与制导学报，2005，25(2): 85-87.

[16] 王智杰，陈伟芳，李浩. 旋转弹丸空气动力特性数值解法[J]. 国防科技大学学报, 2003, 25(4): 15-19.

(编辑：崔贤彬)

Numerical prediction of the Magnus effect for twist fin swept flight projectile

ZHAO Bo-bo1, 2，LIU Rong-zhong1，GUO Rui1，ZHANG Di3，YUAN Jun1，CHEN Liang1

(1.School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China; 2.73917 Troops of the Chinese People's Liberation Army, Nanjing 210094, China; 3.The Chinese People's Liberation Army Military Academy, Hefei 230000, China)

In order to improve flight stability of swept flight assault roof (SFAR)projectile under high rotation speed, Magnus effect pneumatic mechanism of projectile bodies-twist fin combination in flight was studied by using numerical method and the numerical method was validated by using experimental data of BFM model.On the basis of using standard tail experimental data to validate the numerical method, the variation of Magnus effect with the changing rule of attack angle of flat tail and twist tail projectile model was studied. In view of the projectile wing assembly, Magnus effect mechanism was analyzed thoroughly. The results show that twist fin can effectively improve the pressure distribution of wing surface and reduce Magnus effect interference of projectile bodies to wing surface, especially for big attack angle; larger projectile body Magnus force is mainly focused on coccygeal vertebra which is distorted of the vortex symmetry closed to centroid ; Due to projectile interference and geometric profile effect ,empennage lateral force is mainly concentrated on tail.The values of torgue are not much different from each other, while the directions are quite the contrary.

fluid mechanics；twist fin；rotate finned projectiles；Magnus effect；numerical simulation

2014-05-14；

：2014-08-11。

国家自然科学基金(11372136)；国家部委资助项目。

赵博博(1989—)，男，博士生，研究方向为弹箭总体设计及气动优化。E-mail:zhao-bo-bo@163.com

V211

A

1006-2793(2015)04-0465-07

10.7673/j.issn.1006-2793.2015.04.003