火箭拖网系统飞行特性研究

沈 剑，韩 峰，陈 放，陈 翰

(北京理工大学 爆炸科学与技术国家重点实验室，北京 100081)



火箭拖网系统飞行特性研究

沈 剑，韩 峰，陈 放，陈 翰

(北京理工大学 爆炸科学与技术国家重点实验室，北京 100081)

柔性拖网在火箭的拖拽作用下飞行动力学特性较为复杂。利用二维火箭拖网系统的集中质量模型来对其展开研究，并按照计算得到的结论设计了火箭拖网系统并进行靶场飞行试验。通过对比仿真与试验中火箭速度、加速度和方位角3个参数，得到了火箭拖网系统基本的飞行动力学特性，并指出拖网材料力学性能的测试偏差导致了仿真与试验结果的差异。

火箭拖网系统；飞行试验；集中质量模型

0 引言

火箭拖网系统是以小型固体火箭作为动力源，将悬挂在储存箱中的柔性拖网拖拽飞向指定地点, 通过绳网连接发射点和目的地。拖网火箭运动同时兼顾了火箭刚体运动和柔性网变质量系统运动的特点，与一般火箭刚体运动有很大差别，特别是柔性网的运动会对火箭运动产生较大影响。

国内外对于火箭拖网技术的研究相对较少。Mark Frank等[1]提出了一种利用拖网清理战场雷区的方法，文中对于系统各部件作用机理做了简单描述，但并未提出系统的飞行动力学分析过程。与火箭拖网系统相类似的机构，如飞机拖缆、空间飞网和轮船拖网等，在这些领域对于柔性绳网的飞行动力学研究颇为成熟。Paul Williams等[2]对飞机拖拽缆绳的动力学进行了研究，利用集中质量方法建立了缆绳模型，对比了在P-3C原型机、轻型飞机和战斗机三种拖拽体的作用下缆绳不同的动力学特性；吴小平等[3]研究了火箭爆破器在战场扫雷过程中火箭和爆炸带的运动，通过建立爆破器运动方程，分析了拖缆火箭的特性，为拖缆火箭的设计提供了依据；陈钦等[4]针对一种空间碎片处理的飞网系统进行了仿真和试验研究，通过试验结果说明了集中质量模型用于飞网发射建模的可行性；Mankala K K等[5]利用连续体模型建立了绳系卫星系统中牵引子星绳索的模型，并利用Matlab中ODE求解器仿真了系统模型。拖网模型的建立需要确定是否考虑网体弹性变形，是否考虑网体弯曲形变，模型是离散型还是连续型[6]。国内外众多研究结果表明，集中质量模型可有效地用于柔性网动力学分析，同时考虑网体关键的外部气动力和内部的弹性变形因素。虽然这种模型求解精度较低，但建立的常微分方程便于计算，适于工程应用。

本文首先在二维平面上推导刚体火箭和离散质点拖网混合运动方程，利用四阶龙格库塔方法求解模型；再根据数值仿真结果，设计试验用火箭拖网系统，模拟系统真实工作环境进行试验。通过这两项研究，可为该类火箭拖网系统的进一步设计提供重要参考依据。

1 火箭拖网系统运动分析及建模

1.1 拖网运动过程分析

火箭拖网系统的平面模型如图1所示。

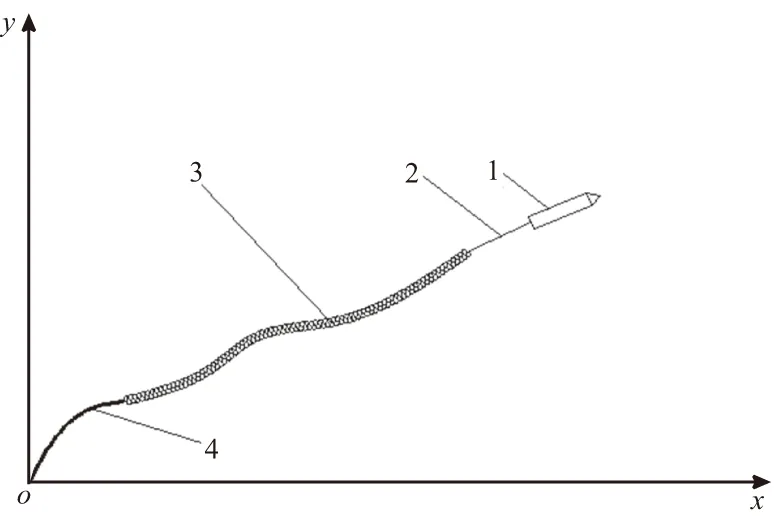
图1 火箭拖网平面模型示意图Fig.1 Rocket towed net model

图1中牵拉钢丝绳长3 m，拖网长度为30 m，回拉绳4 m。火箭拖网飞行过程可分为4个阶段：

(1)滑轨段

这一阶段指火箭从开始点火到脱离发射导轨的运动过程。此过程中，火箭的初始发射参数，如射角和发射位置，决定了弹道曲线的弧度和跨度。

(2)主动段

指拖网火箭脱离导轨后一直到发动机停止工作这一段的飞行过程，储存箱中的拖网一块接一块地被拖出，网上各质点受到的拉力变化剧烈。

(3)被动段

主动段结束后，由于惯性作用，系统继续向前飞行，回拉绳还未开始作用(未发生弹性变形)。

(4)回拉段

回拉绳开始作用，通过弹性变形产生拉力为系统降速，使拖网能较好地拉伸展直，铺设至既定区域。

1.2 拖网系统运动模型

1.2.1 模型假设

(1)火箭拖网运动简化为平面运动。火箭拖网系统初期研究中主要分析系统在整个弹道上的运动特性，即对系统在沿发射方向铅垂平面中的运动过程进行研究，忽略横风作用。

(2)火箭无推力偏心，无绕弹轴自旋运动。火箭的推力在1 kN左右，前期仿真结果可得拖网对火箭的拉力变化在10～100 kN范围内，远大于推力。即使有一定的推力偏心，推力偏心矩对于火箭运动的影响也远不及拖网拉力矩的影响程度大，可忽略不计。

(3)二维柔性拖网离散为N个单元，各单元质量简化到质点上，质点间为无质量、可伸长的柔性连接，且只受拉力作用不受弯矩、压力作用[7]。

1.2.2 火箭刚体运动方程

拖网火箭受力分析如图2。图中，F为火箭推力，Rs为升力，Rz为阻力，T1为钢丝绳对于火箭的拉力，G为重力，vc为火箭质心速度，θ为弹轴与水平方向夹角，α为火箭速度方向与水平方向夹角，L0为质心c到火箭尾端1点的距离，Mz为静力距。

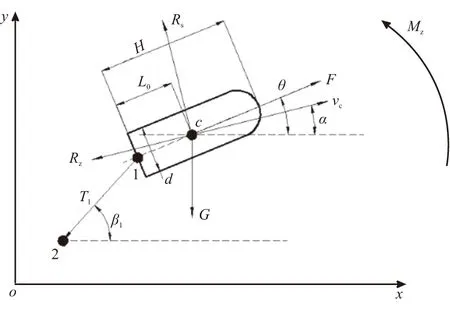
图2 拖网火箭受力分析Fig.2 Mechanical analysis of towed net rocket

根据刚体火箭运动建模方法，建立拖网火箭的运动方程：

(1)

式中LT为布撒网相邻两质点间的距离；ω为弹轴绕质心旋转角速度；J为火箭绕质心转动的转动惯量；ΔL1(t)为1号质点与2号质点间距的伸长量；δ为火箭运动攻角，δ=θ-α。

对方程进行降阶处理，补充方程：

(2)

1.2.3 拖网运动方程

根据模型假设，拖网运动简化为离散质点网体的平面运动。火箭与钢丝绳连接点标记为1，之后的质点依次排序。被拖起的新质点，其初始运动状态与前一点保持一致[8-9]。

拖网受力分析如图3。图中，Ti为质点i对于质点(i+1)的拉力；Rzi为单元(i-1)阻力；Rsi为单元(i-1)升力；Gi为质点i质量；vi为质点i速度；βi为Ti与水平方向夹角。

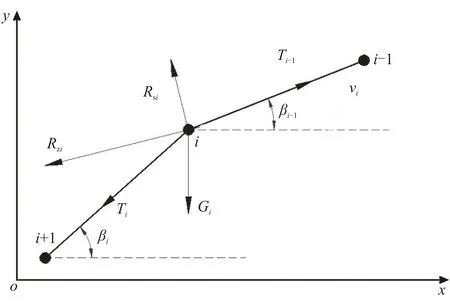
图3 拖网受力分析Fig.3 Mechanical analysis of towed net

建立拖网的运动方程：

(3)

1.2.4 各作用力和静力矩分析

(1)拉力

拖网拉力的公式可表示为

(4)

式中E为网体单元的弹性模量；A为网体单元的迎风面积；ΔLi(t)为i号质点与i+1号质点间距的伸长量；m为拖网最后一个质点编号。

(2)空气阻力

弹箭弹道学中对于弹丸的空气阻力定义为

(5)

式中Rs为升力；Rz为阻力；ρ为空气密度，ρ=1.205 kg/m3；A为火箭迎风面积；Cs为升力系数；Cz为阻力系数。

对于网体离散单元也可看成是圆柱体，Rzi和Rsi可利用分析火箭空气阻力的方法来近似。

(3)静力矩Mz

静力矩的表达式：

Mz=Rzhsinδ+Rshcosδ

(6)

式中h为火箭压心到质心的距离，计算中取h=0.1H[10]。

2 数值仿真与分析

在火箭发射前，拖网悬挂在储存箱中，火箭从地面发射，如图4所示。

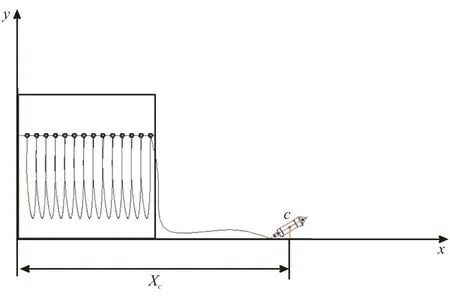
图4 发射前的火箭与悬挂式拖网Fig.4 Towed net and rocket before launching

在MATLAB里编程求解系统运动常微分方程组。计算中按照拖网实际搭放方式赋予每一个质点初始位置。计算得到系统的弹道特性如图5所示。算例初始条件如表1所示。

表1 初始条件Table1 Initial conditions

图5(a)显示的是弹道曲线，弹道高度5.53 m，射程37.80 m，火箭牵拉网体较好地展开；图5(b)是在整个弹道中火箭质心速度变化情况，火箭初速17.12 m/s，最大速度33.52 m/s，平均速度20.15 m/s；图5(c)显示的是受最大拉力的质点拉力随时间变化的情况，其中Tmax=70 401.53 N，该质点位于拖网前部；图5(d)显示的是火箭弹轴与水平方向夹角随时间的变化情况，整个弹道上角度在0.5 s之后基本保持在-50°～50°之间。

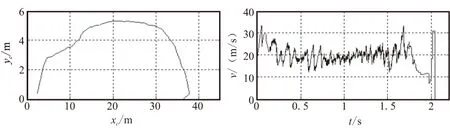
(a)弹道曲线 (b)质点速度

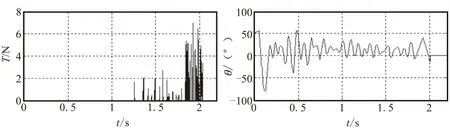
(c)质点拉力 (d)俯仰角

图6(a)～(c)分别显示的是牵拉钢丝绳，拖网以及回拉绳上的拉力随时间变化曲线。其中钢索所受的最大拉力为61 927.07 N，拖网最大拉力70 401.53 N，回拉绳最大拉力27 622.25 N。已知拖网上各质点受拉力情况，在保证强度的前提下选择合适的牵拉钢丝绳、拖网和回拉绳的材料。

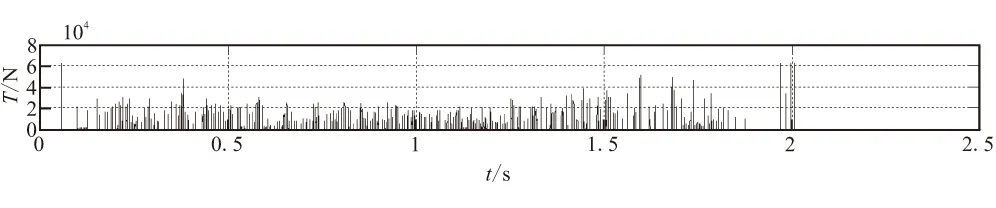
(a)牵拉钢丝绳

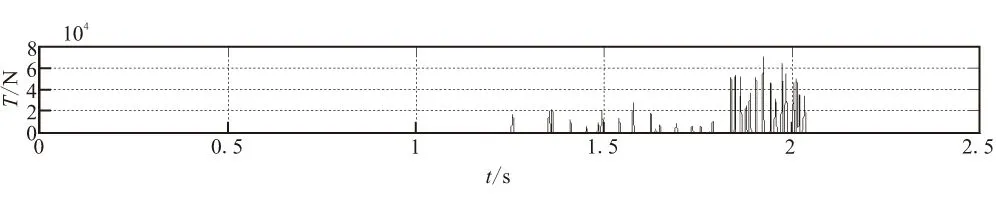
(b)拖网

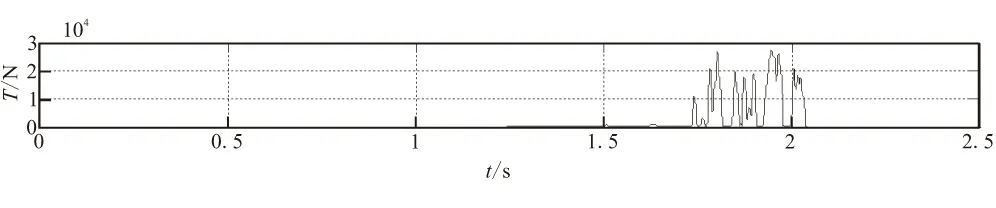
(c)回拉绳

3 试验验证

为了验证火箭拖网飞行的可行性，检验试验设备设计的合理性，进行了靶场实地试验。试验采用高速摄影对试验过程和结果进行了全程记录。试验前各设备状态如图7所示。

试验条件：火箭实测射角50°，火箭质量4 kg，滑轨长度0.5 m，拖网悬挂梁离地面高度1.5 m，拖网线密度3.5 kg/m，长30 m。试验和仿真结果对比如表2和图8所示。

仿真和试验结果显示火箭拖网距离均达到32 m以上，网体基本展开，达到预期效果。并且火箭在牵拉网体飞行过程中，从弹道0.2 s时刻之后，火箭速度在20 m/s左右浮动，俯仰角处于-50°～50°之间，说明了系统工作可靠，设计方案较为合理。

图7 火箭拖网系统试验前Fig.7 Rocket towed net mine sweeping system before test

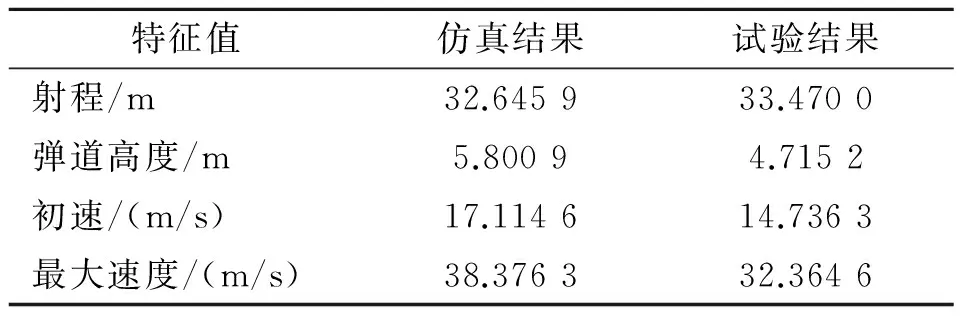
表2 试验与仿真结果弹道特征值对比Table 2 Comparison of exterior ballistics parameters between test and simulation

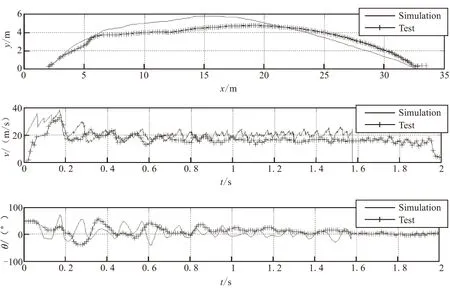
图8 火箭拖网系统试验结果与仿真计算对比Fig.8 Comparison between test result and simulation of rocket towed net mine sweeping system

对比仿真和试验结果，不难发现二者之间存在着部分差异。究其结果就是在于牵拉钢丝绳、拖网和回拉绳在飞行过程中其上拉力变化在试验中无法测试，而试验前期各部件力学性能采用的是静态方法测试，与真实飞行过程中拖网受动载荷作用有部分差别。仿真结果只是近似模拟真实情况，由于各部分力学性能未能按照实际情况在仿真计算中进行设置，导致了误差的出现。

4 结论

(1)集中质量模型在工程上可用于模拟火箭拖网系统动力学过程。

(2)拖网在飞行过程中由于自身的柔性体的特点，网带上的拉力变化频率较高，这为网带材料的选取提出了要求，即在满足强度要求的前提下尽可能地选取弹性模量较大的材料。

(3)拖网的拉力作用使得火箭飞行过程中的摆动趋于稳定，但试验过程中发现网体上产生了一定的波动，后期可选择弹性更优的材料来减弱。

(4)火箭拖网系统运动特性在平面内得到了较好地模拟，接近飞行试验结果。对于下一步仿真工作，可继续采用集中质量模型建立拖网三维模型，分析系统空间运动特性；对于系统各部件力学性能，则应利用动态方法来获得，以期更逼近真实网体材料模型。

[1] Mark Frank,Richards,L McDuffie,Christopher Kohl,et al.Method for breaching a minefield [P].US:US8037797B1.Oct 18,2011.

[2] Paul W,Pavel T.Dynamics of circularly towed aerial cable systems,Part I:Optimal configurations and their stability[J].Journal of Guidance,Control,and Dynamics 2007;30:753-765.DOI:10.2514/1.20433.

[3] 吴小平,郑友祥,丘光申.拖缆火箭弹道计算研究[J].弹道学报,1995,7(1):41-49.

[4] 陈钦,杨乐平,张青斌,等.空间飞网发射动力学建模仿真研究与地面试验[J].国防科技大学学报,2009,31(3):16-19.

[5] Mankala K K,Agrawal S K.Dynamic modeling and simulation of impact in tether net π gripper systems[J].Multibody System Dynamics,2004,11(3):235-250.

[6] 陈钦.空间绳网系统设计与动力学研究[D].长沙:国防科学技术大学,2010.

[7] Han F,Chen H,Zhu Q. Modelling and simulation of a rocket-towed net system[J].Int.J. Modelling, Identification and Control,2013,20(3):279-285.

[8] 吴宏,侯吉忠,纪建华.直列装药火箭爆破器中火箭对钢丝绳拉力的计算[J].弹箭与制导学报,2002,22(3):59-61.

[9] 张登成.拖曳式重复使用运载器飞行动力学[D].西安:西北工业大学,2005.

[10] 王军波,张军挪,高敏,等.滑翔增程弹稳定储备量的优化设计与仿真[J].华北工学院学报,2005,26(2):103-106.

(编辑：吕耀辉)

Flying characteristics of rocket towed net system

SHEN Jian，HAN Feng，CHEN Fang，CHEN Han

(State Key Laboratory of Explosion Science and Technology，Beijing Institute of Technology，Beijing 100081，China)

In order to find the characteristics of rocket towed net system,the lumped mass model of rocket towed net system was established in plane.Then,the rocket towed net system was designed and tested in the shooting range.According to the comparison with rocket velocity,acceleration and azimuth,the basic dynamical characteristics of rocket towed net system have been obtained.Additionally,the test deviation of net material mechanical property resulted in the differences between simulation and test.

rocket towed net system；flying test；lumped mass model

2014-07-03；

：2014-08-04。

沈剑(1988—)，男，博士，研究方向为火箭柔性拖网动力学。E-mail：sword-sh@163.com

V435；TJ51+8

A

1006-2793(2015)04-0477-04

10.7673/j.issn.1006-2793.2015.04.005