再入飞行器多约束姿态控制律设计
李宪强,周 军
(西北工业大学 精确制导与控制研究所,西安 710072)
再入飞行器多约束姿态控制律设计
李宪强,周 军
(西北工业大学 精确制导与控制研究所,西安 710072)
针对存在干扰、输入约束和状态约束的再入飞行器,提出了一种面向控制性能的三环控制方案。该控制方案的具体结构是内环中设计了一种自适应滑模控制方法,以保证系统能够有效跟踪在线规划的最优参考模型;外环在考虑系统不确定性,且不违反控制约束和状态约束的前提下,利用在线优化算法,设计一种动态性能最优的参考模型;中环设计了一种干扰边界估计算法,以对外环在线规划最优参考模型时提供辅助手段。经过仿真验证,所提出的三环控制方案不仅能够保证系统具有很好的稳态性能,而且能够保证系统具有快速收敛的动态性能。
再入飞行器;控制约束;控制性能;参考模型
0 引言
目前在控制系统设计中,不仅要求控制系统具有良好的稳态特性,而且对系统动态特性的要求越来越高。但实际系统常存在着输入约束和状态约束,而且还存在着干扰特性和未建模动态。对于此问题,目前绝大多数文献都是在关注稳态特性的前提下,兼顾动态特性。因此,对系统动态特性重视不足,进而使得系统的动态特性有待进一步提升。例如,为了使得系统具有更好的稳态特性,常采用高增益控制[1]、鲁棒控制[2,3]、自适应控制[4]或者变结构控制[5~7]等方法。这些方法确实具有很好的抗干扰特性,但当状态和控制输入存在约束,且初始偏差较大时,为了保证系统满足约束,参数的选取往往具有保守性。因此,难于保证系统在整个收敛过程中的动态特性。相比以上比较关注稳态特性的控制方法,最优控制[8-9]能够保证系统具有良好的动态特性,但最优控制方法的抗干扰能力不强,当系统存在强干扰时,难于保证系统的稳态特性。因此,最优控制方法在实际中应用较少。
根据以上分析可知,在系统存在干扰和约束的前提下,如何同时保持良好的稳态特性和很快的收敛速率的问题,目前还没有很好的解决方法。对此,本文提出了一种三环控制方案。该控制方案,外环在满足控制约束和状态约束的前提下,以收敛速率为指标函数,通过在线寻优,设计了动态特性最优(收敛速率最快)的参考模型,值得说明的是该在线寻优方法的计算量不大,因此不存在难于实现的问题;内环设计了一种自适应滑模控制方法,用来保证系统在存在干扰情况下,依然能够对外环最优参考模型进行稳定且精确地跟踪;中环设计了一种干扰估计方法,用来提供干扰的边界,以降低外环在搜寻最优参考模型时的保守性。以上三环控制方法不仅能够保证系统具有良好的稳态特性,而且还能够保证系统具有最快的收敛速率,这是目前已有的控制方法中所不具备的。
1 问题描述
针对如下数学模型:
(1)
其中,x1和x2为状态;y为输出;d为干扰;f(x1,x2)为已知项;sat(u)为具有饱和特性的输入:
(2)
式中u_MAX为最大可用输入。
在实际,中状态会存在约束取值范围:
(x1,x2)∈Ωx
假设期望的跟踪轨迹yd满足:
(4)
本文要解决的问题是在状态和输入都存在约束的情况下,输出y能够尽可能快地跟踪期望的轨迹yd,且跟踪误差尽可能的小。
2 控制器结构
设计一种三环控制结构(见图1),具体如下:
(1)外环路主要是用来对跟踪轨迹yd进行重新规划,具体步骤是在采样周期T内,考虑存在输入饱和、状态约束以及干扰边界值的情况下,寻优出能够以最快速率收敛的参考模型yr。
(2)中环路是用来估计干扰的边界,以提供外环寻优参考模型时所需的干扰边界值,这样可降低外环寻优参考模型时干扰边界取值的保守性。
(3)内环路设计了一种自适应滑模控制,主要用来保证系统在存在干扰及不确定情况下,能够精确跟踪外环规划出的最优参考模型。
值得注意的是,外环的采样周期时间尺度应大于内环,以保证能够有效寻优出最快的收敛模型。
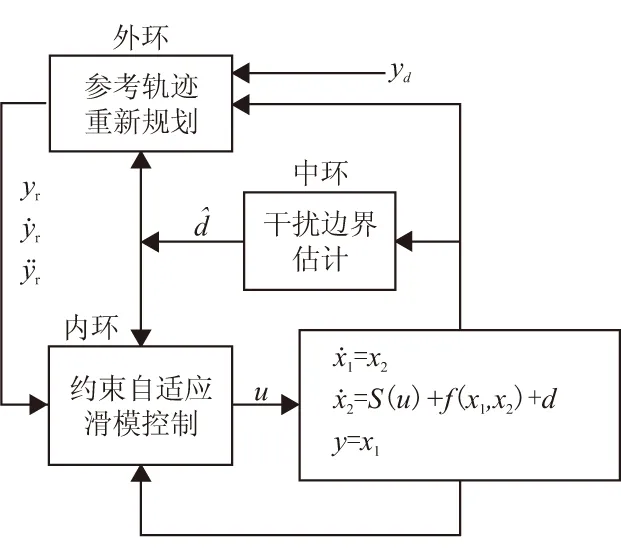
图1 控制结构框图Fig.1 Structure of the controller
3 内环自适应滑模控制方法

(5)
将式(5)中具有饱和约束的输入写成如下形式:
sat(u)=χ(u)·u
(6)
(7)
其中,χ(u)∈(0,1)为输入的饱和程度,χ(u)越接近0,则饱和程度越严重,等于1时,则没有饱和。
定理1:在如下控制器的控制作用下,系统式(5)的状态将是渐进稳定的,即e=[e1-e2]T→[0 0]T。
(8)
其中,m>0,n>0。
滑模面为
s(t)=ce1+e2
(9)
式(8)中的自适应项为
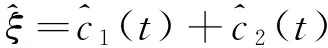
(10)
其中,自适应律为
(11)
式中p1和p2为待设计的正常值。
证明:针对系统(5),选择李雅普诺夫函数:
(12)
对式(9)求导,并代入式(5),可得
(13)
对式(12)进行求导,并代入式(13),可得
(14)
根据式(14),可得

(15)
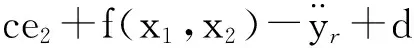

(16)
根据式(6)和式(7),并结合式(16),可得
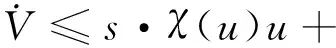
(17)
假设饱和函数χ(u)存在不为零的下界,即存在一个非零常值σ满足0<σ≤χ(u)≤1。结合式(8)、式(10)和式(17),可得
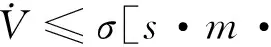

|s|(c1+c2|e1|)
(18)
根据式(18),进一步可得


(19)
将式(11)代入上式,可得

(20)

(21)
根据式(19)~式(21),可得

≤-σs·n·sgn(s)≤0
(22)
根据李雅普诺夫理论可知,s能够有收敛到零点。在滑模面上,选择c>0时,显然状态是渐进收敛的,即e=[e1e2]T→[0 1]T。
注1 :文中饱和度函数定义如式(7)。因此,只有当输入u不为无穷大时,饱和度函数才能不为零。从式(17)~式(18)的证明过程中,假设饱和度函数的下界σ不为零是合理的。
注2 :σ仅在证明过程中用到,没有出现在控制器中。因此,不需要在线估计σ的值。
注3:以上内环控制器,在三环控制回路中的作用是用来保证系统在存在干扰情况下,对外环最优参考模型进行精确跟踪。
4 中环干扰边界估计方法
根据跟踪误差动态方程(5),设计干扰观测器,以估计干扰的大小和边界。本章的主要作用是降低外环在线搜寻最优参考模型时对干扰边界取值的保守性。
定理2:存在如下方程:
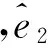
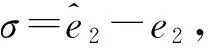
(24)

5 外环动态性能最优的参考模型设计
在初始时刻,初始值与yd的偏差较大时,如果yd被直接用来作为参考模型,控制系统将会出现输入饱和或者状态不再满足约束等情况,从而使得动态性能无法保证。因此,为了防止不满足约束的情况发生,需要对yd进行修正。修正时,在满足控制约束和状态约束范围的前提下,修正后的参考模型yr应以最快的速率收敛到yd,以保证动态特性最优。接下来,采用在线寻优方法,在满足各种约束的前提下,寻求能够以最快的速率收敛到yd的在线最优参考模型yr。
令式(1)中的:
M=sat(u)+f(x1,x2)+d
(25)
且令重新规划的参考模型具有如下形式:
(26)

接下来,基于式(26),通过在线寻优,给出最优参考模型。首先,根据式(26),可得
(27)
建立如下寻优算法:
(28)
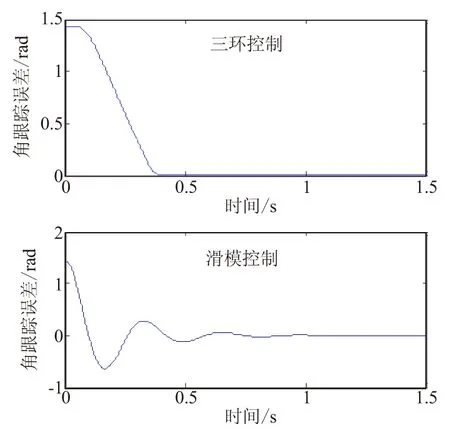
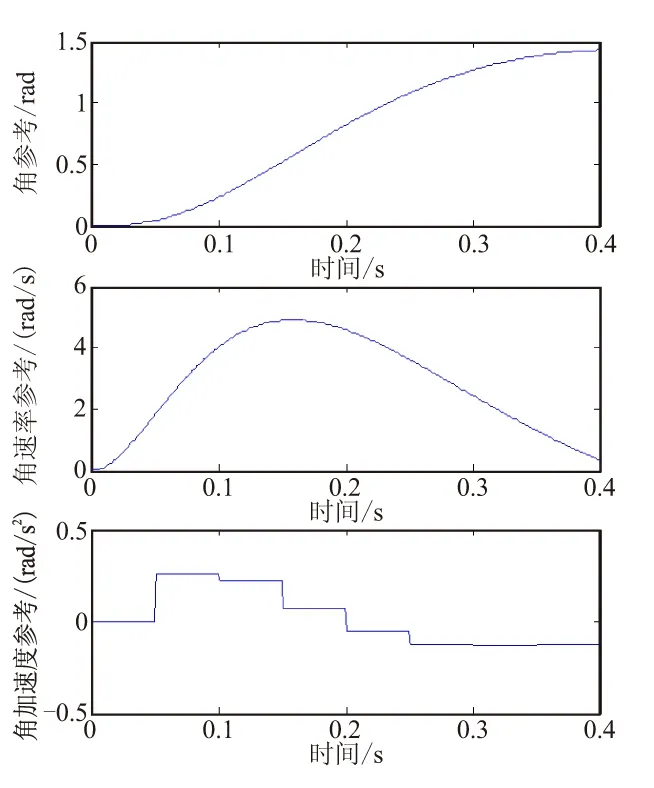
以上寻优算法为三环控制提供了最优的参考模型。具体来说,在t 采用BTT控制形式的再入飞行器滚转通道的数学模型如下[11]: (29) (30) 以上模型存在如下输入约束: (31) 状态约束如下: (z1,z2)∈Ω (32) D和c1ωx分别满足 D=0.2sin(3t+0.5) (33) c1ωx∈Ωd{c1ωx||c1ωx|≤0.9} (34) 滚转角初值为z1=-0.5 rad,滚转角速度初值z2=0,期望的角跟踪指令为yd=1 rad。 接下来,采用文中的三环控制方法,对式(30)所示的系统进行仿真。作为对比,设计如下滑模控制方法[12],令滑模面 s=z2+az1 (35) (36) 取如下趋近律: (37) 对比式(36)和式(37),可得滑模控制律如下: (38) 仿真对比结构见图2~图4。 图2 姿态角跟踪误差收敛效果图Fig.2 Responses of the attitude tracking error 图3 输入对比结果图Fig.3 Control inputs under the two different controllers 根据图2可知,当存在干扰时,本文的三环控制和滑模控制都具有很好的稳态特性,即抗干扰能力强、控制精度较高。但本文提出的三环控制的动态特性要远好于滑模控制的动态特性,即三环控制能够控制跟踪误差以最快的速率收敛,而滑模控制方法的误差收敛曲线发生了振荡。根据图3可知,本文提出的三环控制的输入始终在约束范围内,而滑模控制的输入则出现了饱和现象。 图4 三环控制中外环参考模型Fig.4 Optimal reference model designed in the outer loop 造成以上结果的原因是三环控制方法在设计控制器时就考虑了,在存在约束前提下,系统的动态特性如何最优的问题。而滑模控制的设计过程过分关注稳态特性,对动态特性关注不足,从而导致在存在约束情况下,动态特性无法保证。具体表现就是当初始偏差较大时,滑模控制参数的选取变得困难,很容易导致控制输入的饱和(图3)。当控制输入饱和后,系统变成了开环系统。因此,系统的动态特性难于保证,从而造成了图2中滑模控制跟踪误差收敛曲线的振荡现象。而图3中三环控制方法的控制输入始终没有发生饱和,且跟踪误差能够以最快的速率收敛,这是由于外环控制在提供最优参考模型时,充分考虑了系统的输入约束和状态约束。所以,只要内环能够有效跟踪外环最优参考模型,就不会发生控制输入饱和现象,而且由于外环提供的是动态特性最优(收敛速率最快)的参考模型。因此,只要系统能够有效跟踪,就能够保证控制系统以最快的速率收敛。图4给出了外环最优参考模型,显示了在0.4 s时,外环最优参考模型跟踪上了系统期望信号。据图4可看出,外环系统每间隔0.05 s给出一次参考指令,而且在初始偏差较大时,给出的指令很小,从而防止控制系统不满足约束的现象发生。 针对多约束系统设计了一种面向控制性能的三环控制方案,该方案提供了一种面向控制性能的新型控制结构和相应实现方法,该三环控制具有以下特点: (1)通过设计充分考虑系统约束的最优参考模型,使得控制输入在整个控制过程中都不会发生饱和。而且在设计最优参考模型时,充分考虑了系统的收敛速率,能够确保整个收敛过程中都以最快的速率收敛。 (2)通过设计新型的约束自适应滑模控制方法,确保控制系统具有良好的抗干扰特性和稳态精度。 (3)本文三环控制方法在具有良好稳态性能和动态性能的同时,结构简便,易于实现。 [1] Ridgely D B, Banda S, Dazzo J. Decoupling of high-gain multivariable tracking systems[J]. Journal of Guidance, Control, and Dynamics, 1985, 8(1): 44-49. [2] Liu Ming, Zhang Li-xian, Shi Peng, et al. Robust control of stochastic systems against bounded disturbances with application to flight control[J]. IEEE Transactions on Industrial Electronics, 2014, 161(3):1504-1515. [3] Yoonghyun Shin, Anthony J Calise, Matthew Johnson. Adaptive control of advanced fighter aircraft in nonlinear flight regimes[J]. Journal of Guidance, Control, and Dynamics, 2012, 31(5): 1464-1477. [4] Dydek Z T, Annaswamy A M, Lavretsky E. Adaptive control of quadrotor UAVs: A design trade study with flight evaluations[J]. IEEE Transactions on Control Systems Technology, 2013, 21(4): 1400-1406. [5] Geng J, et al. Second-order time-varying sliding mode control for reentry vehicle[J]. International Journal of Intelligent Computing and Cybernetics, 2013,6(3):272-295. [6] Stotta J E, Shtessel Y B. Launch vehicle attitude control using sliding mode control and observation techniques[J]. Journal of the Franklin Institute, 2012, 349(5):397-412. [7] Sun H B, Li S H, Sun C Y. Finite time integral sliding mode control of hypersonic vehicles[J]. Nonlinear Dynamics, 2013, 73(7): 229-244. [8] Audrey Hermant. Optimal control of the atmospheric reentry of a space shuttle by an homotopy method[J]. Optimal Control Applications and Methods, 2011, 32(6): 627-646. [9] Donald E Kirk. Optimal control theory: an introduction[M]. Dover :Dover Publications, 2004 . [10] Tenoch Gonzalez, Moreno,Leonid Fridman. Variable gain super-twisting sliding mode control[J]. IEEE Transactions on Automatic Control, 2012, 57(8): 2100-2105. [11] 周军, 周凤岐, 冯文剑, 等. 基于变结构控制理论的BTT导弹自动驾驶仪的三通道独立设计[J]. 宇航学报, 1992, 20(1): 42-47. [12] 孙长银, 穆朝絮, 张瑞民. 高超声速飞行器终端滑模控制技术[M]. 北京: 科学出版社, 2014: 117-128. (编辑:吕耀辉) Controller design for the reentry vehicle under multi-constraints LI Xian-qiang,ZHOU Jun (Institute of Precision Guidance and Control, Northwestern Polytechnical University, Xi'an 710072, China) A performance oriented three-loop control scheme is proposed, under the input and state constraints. The specific structure of the control scheme is that, an adaptive sliding mode controller is designed in the inner loop which is used to track the reference model replanted online, and the reference model is designed in the outer loop through using online optimization algorithm, in which the uncertainty and the state constraints are well considered. The bound of the disturbance is estimated in the middle loop, and is used in the design process of the reference model. The three loop controller can not only insure a steady performance, but also insure a fast convergence of dynamic performance. And the efficacy of the method is demonstrated through simulation. reentry vehicle; control constraints; control performance; reference model 2015-02-12; :2015-03-23。 国家自然科学基金(61304238); 国家863项目(2012AA120602)。 李宪强(1986—),男,博士生,研究方向为导航、制导与控制。E-mail:1740679934@qq.com V448 A 1006-2793(2015)04-0472-05 10.7673/j.issn.1006-2793.2015.04.0046 三环控制方法在再入飞行器滚转通道控制中的应用






7 结论

