基于均衡性的机车乘务排班计划编制方法研究

王兴慧，颉俊杰

（兰州交通大学 交通运输学院，甘肃 兰州730070）

随着铁路建设的迅速发展，铁路实现了前所未有的高速度，但铁路在运营过程中安全隐患却始终存在，影响铁路安全的因素很多，其中的机车乘务员是一个主要因素，作为机车的驾驭人，由于机车乘务员疲劳而引发的事故比较常见，机车乘务人员的技术高低以及工作状态的好坏直接影响到铁路行车的安全，因此，为了保证行车安全，调度人员以及排班人员要高度重视机车乘务人员的工作状态，深入研究排班计划理论与编制方法。一个好的排班计划对于调动工作人员的工作热情、提高生产效率具有积极作用，能够给企业创造巨大的财富。

在现有的乘务排班方法中，李成兵利用熵评价排班计划的均衡性，并且给出了均衡度的计算方法，为月排班计划奠定了理论基础。赵鹏利用SE方法实现排班的自动化，大多数研究者都将排班问题看作是旅行商（TSP）问题，将乘务基地作为城市，乘务基地之间的接续看作城市之间的衔接，采用了经典的遗传算法或是在遗传算法基础上进行改进的算法求解。

1 影响排班计划的主要因素

乘务排班计划是合理安排乘务员的基础，在交路确定的条件下，调度人员根据相关规定对乘务员在什么时间和地点值乘哪辆机车出发，在某时某地换乘另外一辆机车或是退乘都做出了详细安排，以确保列车准点、高效地运行，排班时应考虑的因素如下:

1.1 乘务交路

乘务交路是排班计划的基础，交路主要包括两个规则:交路时间规则和交路空间规则。

1）交路时间规则约束:值乘乘务交路时，前一个值乘交路的到达时间早于后一个值乘交路的出发时间，使交路的接续顺序合理。此外，还必须满足规定的乘务时间规则，这是判断交路是否可行的必要条件，具体的时间规则约束如表1所示。

表1 乘务时间规则约束表

2）交路空间规则约束:在值乘交路时，乘务员值乘交路的到达地点与下一接续的交路出发地点必须是同一地点，这样保证了空间连续性，还应该考虑乘务员的休息地点问题，尽量使乘务员的出发地点与结束地点在同一个乘务地点。

1.2 乘务制度方式

现有的机车乘务员值乘方式大多采用的是轮乘制，这种方式一方面有利于排班人员合理安排乘务人员的工作和休息时间，使得排班灵活；另一方面可以不用考虑机车因等待乘务员而浪费时间，提高了机车效率，同时也增加了对乘务员的使用效率。

2 基于均衡性的机车乘务排班计划编制

2.1 排班问题分析

乘务排班计划是在乘务交路计划制定好的前提下进行的，即每天给每条交路安排好乘务人员，形成乘务组连续值乘的排班计划。但在排班过程中，交路不同，交路的长度也不相同，若将每条交路固定给特定的一组或几组乘务员值乘，那么各个乘务组之间的工作时间也不一样，必然会出现乘务组间的不均衡现象。因此，基于上述原因的考虑，在乘务交路数量一定的情况下，将所有交路组合成一个有序回路，使乘务员根据这个回路循环进行轮换工作，这种排班方式大大消除了乘务组间由于担当交路不同而产生的工作量不均衡问题，这种方式被称为单循环乘务排班。

在单循环乘务排班方式中，排班人员根据乘务员所承担的工作量，合理添加乘务员的休息时间，表2是一个短周期的单循环排班示意表。

表2 单循环排班示意表

2.2 单循环乘务排班计划模型的建立

2.2.1 排班问题的目标

通过对单循环乘务排班计划问题的分析，如果将值乘的每条交路看成是旅行商问题中的城市，将交路间的接续时间看作城市与城市间的距离，距离的长度就是两交路的接续时间，那么单循环乘务排班问题可以认为是一个旅行商问题，目标是寻求访问所有回路仅一次的循环顺序，使得总访问时间最短。

其次，乘务员的使用数量也是乘务排班计划中考虑的关键因素，一般情况下，乘务员的使用数量根据乘务交路计划来确定，合理的乘务交路序列是减少乘务员数量的关键，但除了考虑乘务员的正常休息之外，还应考虑一些不确定因素导致乘务员不能按时出乘，所以在实际的排班中，所需乘务员的数量要比乘务交路计划所需的乘务员数量多，因此，在满足乘务规则的基础上，应考虑怎样缩短排班周期，使得乘务员运用数量最少。

在单循环排班方式中，虽然消除了乘务组间工作量不均衡问题，但由于乘务交路起止时间不同，乘务员担当不同的乘务交路后的休息时间也不完全相同，除了规定的标准休息时间外，还会产生一部分冗余时间，因此，使得冗余时间更加均衡也是本文要考虑的一个关键问题。

基于以上问题的考虑，建立模型时应考虑以下两个方面:

1）寻找最优的乘务交路顺序，使得所有交路的接续时间最短，尽可能缩短乘务排班周期，减少乘务员的使用数量。

2）合理安排乘务员的工作与休息时间，尽量使乘务员每次的休息时间与所值乘交路的劳动量相协调。

2.2.2 排班问题的约束条件

单循环乘务排班计划的编制结果是所有乘务交路以最优顺序接续构成的回路，在找寻最优接续顺序时，需满足以下几个条件:

1）乘务排班过程中每个交路仅有一个紧前交路；

2）乘务排班过程中每个交路仅有一个紧后交路；

3）乘务交路间的接续应满足相应的乘务时间规则，根据交路的值乘时间长短，合理的安排正常休息和大休时间。

2.2.3 乘务排班模型的建立

根据以上问题的描述与分析，单循环机车乘务员排班计划的约束条件主要考虑相邻交路间的接续关系，用n表示交路数量，tij表示值乘交路i和值乘交路j间的接续时间，xij表示0～1变量，当交路i的后面交路为j时，xij值为1，否则为0。

首先在乘务排班过程中要找出最优的交路顺序，使得所有交路的总接续时间最小，也就是说使整个排班计划的周期最短。需要建立目标函数，可用下列公式求得

在求解交路接续顺序的过程中，每个不是起点的交路在排班过程中只有一个紧前交路，并且每个不是末尾的交路在排班过程中只有一个后续交路，需要满足的条件为

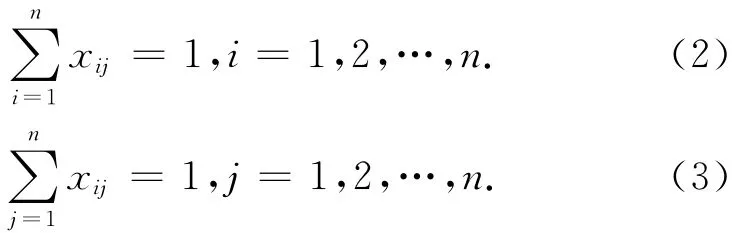
在所有交路遍历完之前，根节点与叶节点的数量必须小于交路的总个数，保证每条交路都被遍历，且只遍历一次，需满足的条件为

其中还需要考虑不会出现交路与交路本身相接续的情况，当i＝j时，tij＝∞，并且交路的起点到终点与交路的终点到起点不具有对称性，因此有tij≠tji。

2.3 排班计划模型求解

2.3.1 算法的选取

由上述模型可以看出，乘务排班问题可以看成是单目标整数规划问题，由于整数变量取离散的整数值，其可行解的数量是有限的，即把问题的解全部列出来，将其比较得出最优解，但可行解的数量会随着问题的规模增大成指数倍的增长，枚举是不可能完成的，分枝定界法是一种求解整数规划问题比较有效的方法。因此，文章采用分枝定界法求解单循环乘务排班计划模型。这里将排班问题的求解分为两部分:

1）利用分枝定界法找出总接续时间和最小的乘务交路顺序；

2）根据乘务时间规则，在最优循序的回路中添加双休日。

2.3.2 算法步骤说明

在文章中只研究相同乘务区段的乘务交路，这样前一个乘务交路到达地点与后一个乘务交路的出发地点始终是同一个地方，任意两条交路之间都可以接续。以图1为例说明算法步骤。

图1 树的构建

2.3.2.1 步骤顺序

Step1:先将所有交路按照出发时间从早到晚进行顺序排序，以A，B，C，D 4个点代表4条交路为例说明，将出发时间最早的交路A作为树的根节点；

Step2:从根节点的交路A开始，依次从左向右深度遍历剩下的所有交路B，C，D，每个节点仅加入一次，并最终回到A；

Step3:先计算出A→B→C→D→A总接续时间，并记住这个接续时间，记为tmin，每次从A遍历，每加入一个节点将接续时间累加记为t，并与tmin比较，若t＞tmin，则停止遍历，舍弃这一分支；若直至遍历到A，依然有t＜tmin，则令tmin＝t；

Step4:依次将所有节点遍历完，使tmin值最小的序列就是所要找的总接续时间最短交路序列。

2.3.2.2 大休时间添加流程

利用分枝定界法获得一条接续时间最短的乘务交路回路，根据乘务时间规则在这条回路中添加休息时间。将乘务员从执行第一条交路开始将工作时间进行累加，记为tsum，将工作时间达到双休时间上限记为T休，其中的大修累计时间参照文献［6］，使T休＝1 969min，交路的总个数为n个，ji记为第i条交路，第i条交路与第j条交路的接续时间记为tij，则添加休息时间的流程如图2所示。

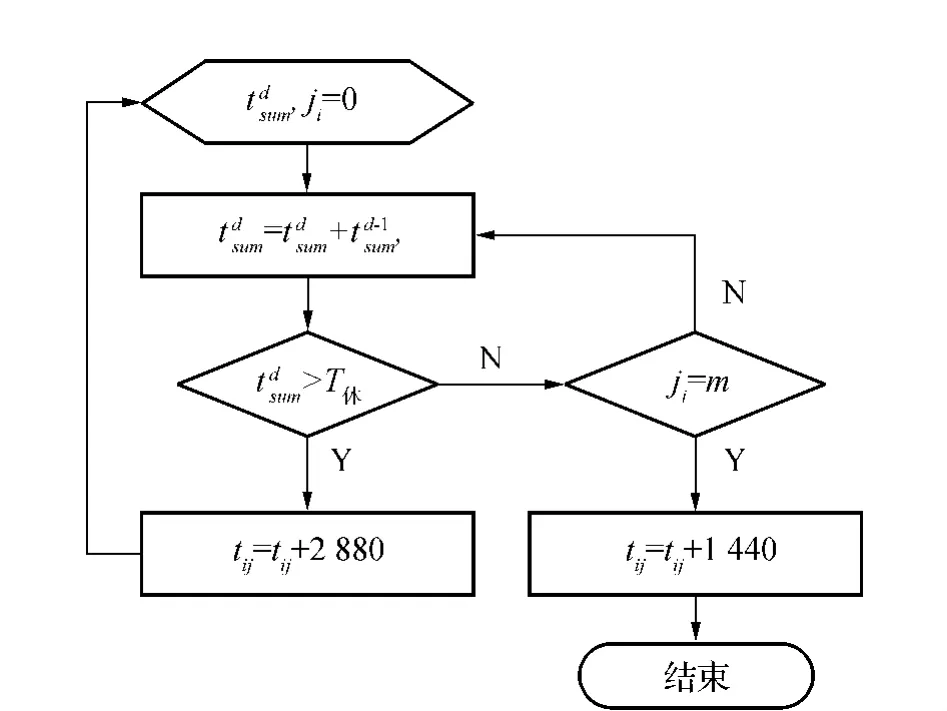
图2 休息时间添加流程

3 算例分析

以京津线的部分交路数据为例验证算法的有效性，表3选取了9条交路，分别给出了每条交路的出发时间和到达时间，根据出发时间和到达时间计算出每条交路的值乘总时间，具体的交路数据如表3所示。

表3 交路时间表

由上面的步骤分析可知，先将所有的交路按照顺序接续，例如交路1和交路6的接续时间为19min，交路2和交路8的接续时间为1 419min，统计接续时间如表4所示。

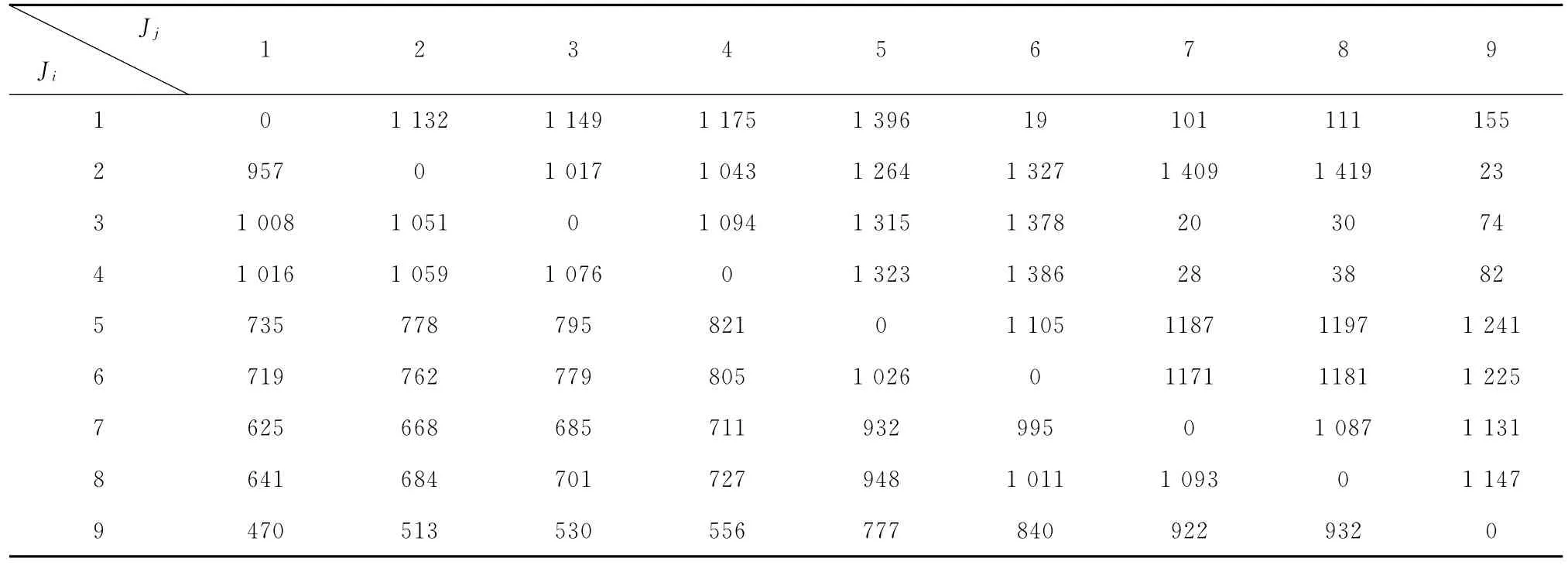
表4 时间接续表

根据上述算法步骤，利用C＋＋语言编写了程序，并在VC6.0环境下实现算法，得到的总接续时间最短、最优，交路回路顺序为:1→6→8→2→9→3→7→4→5→1，最短的总接续时间为5 226min。最优交路循环如图3所示。

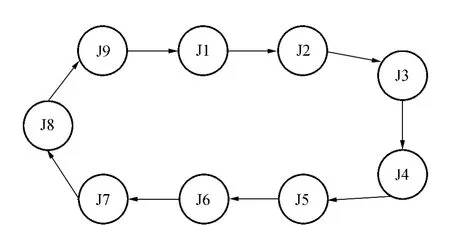
图3 循环交路

按照添加大休时间流程，给得到的循环交路图添加休息时间，结果如表5所示。

根据单循环乘务排班思想，由表5的乘务排班计划结果可看出，这9条乘务交路需要8组乘务员担任。

表5 排班计划表

4 结 论

由上述算法以及实现的结果可以看出，分枝定界法可以有效解决单循环乘务排班问题，合理有效地安排机车乘务员的工作休息时间，使各个乘务组的工作量达到均衡，从而保证了公平公正的原则，这对提高机车乘务员的工作效率、激发机车乘务员的工作积极性具有重要意义。

但利用分支定界法求解单循环乘务排班问题也存在一些不足，此种方法适合乘务交路规模较小的排班，当乘务交路的数量较大时，算法的复杂度比较高，这时就要将乘务交路划分成较小的块来求解或者是寻找更优的方法求解，总之，求解乘务排班问题，还有待于更深入的研究。

［1］ 田志强.高速铁路乘务计划编制优化理论与方法研究［D］.成都:西南交通大学，2011.

［2］ 李成兵，鲁工圆，郭倩倩，等.动车组乘务员运用计划的均衡性研究［J］.内燃机车，2009（12）:31－33.

［3］ 王媛媛，周成晨，倪少权.基于蚁群算法的客运专线乘务交路计划编制方法研究［J］.铁路计算机应用，2009（7）:11－14.

［4］ 郑金子，苗建瑞，张君平.蚁群算法在铁路乘务运用计划编制中的应用研究［J］.铁路计算机应用，2010（10）:36－40.

［5］ 赵鹏，姚凤金，张洪亮.综合调度仿真系统中的机车乘务计划的编制［J］.铁道运输与经济，2005（3）:74－76.

［6］ 柴小树.动车组乘务计划编制方法研究［D］.长沙:中南大学，2013.

［7］ 李志鹏.铁路调车机车运用问题探讨［J］.交通科技与经济，2014，16（6）:47－48，52.

［8］ Shangyao Yan，Yu－Ping Tu.A network model for airline cabin crew scheduling［J］.European Journal of Operational Research，2002（140）:531－540.

［9］ Sydney C.K.Chu.Generating，scheduling and rostering of shift crew－duties，Applications at the Hong Kong International Airport［J］.European Journal of Operational Research，2007（177）:1764－1778.