受简谐激励弹性地基不可伸长梁的主共振响应

马建军,刘丰军,高笑娟,谢 镭

(河南科技大学 土木工程学院,河南 洛阳 471023)



受简谐激励弹性地基不可伸长梁的主共振响应

马建军,刘丰军,高笑娟,谢 镭

(河南科技大学 土木工程学院,河南 洛阳 471023)

基于弹性地基不可伸长梁的非线性动力学模型，对简谐激励下梁的主共振响应进行了研究。利用多尺度方法，求得弹性地基不可伸长梁的主共振幅频响应方程及其横向位移的二次近似表达式，进而运用梁主共振的幅频响应曲线，分析了弹性地基模型、Winkler参数、外激励幅值和边界条件等对梁非线性动力响应的影响。数值分析结果表明：Winkler参数在弹性地基梁的主共振响应中起控制性作用，而剪切参数的引入有利于更精确地展现弹性地基梁的非线性动力学特性，外激励幅值对弹性地基梁的动力学特性基本无影响。

弹性地基；不可伸长梁；主共振；多尺度法；幅频响应曲线

0 引言

弹性地基梁模型在工程结构领域有广泛的应用，可对多种结构物进行简化理论分析[1-2]。随着各学科间的交叉拓展，该模型已逐渐发展成为一类基本力学模型[3-5]。因此，国内外学者对弹性地基梁模型的建模及计算方法进行了大量研究，并提出了单参数、双参数和三参数等地基模型[6]。

鉴于弹性地基梁在工程和理论应用层面的重要性，针对弹性地基梁的线性和非线性动力响应均有一系列研究[7-11]。这些已有研究既丰富了弹性地基梁的应用，又深化了弹性地基梁模型的建模理论[12]。通常而言,工程中的梁为比较大的细长结构物,甚至许多实际梁式结构可认为是无限长的。因此，一般认为弹性地基梁是不可伸长的。理论上讲，若梁的一端约束为自由或滑动铰支，且不承受轴向荷载作用，可假定动力响应过程中梁的中轴线不可伸长，即为不可伸长梁。而且已有研究表明：若充分考虑土-结构相互作用效应在非线性动力学层面的贡献，弹性地基不可伸长梁的非线性运动方程中含有平方非线性项，能为桩基动力学试验中的软弹簧特性提供一种较为合理的理论解释[13]。因此，有必要基于文献[12]，建立弹性地基上有限长梁的非线性动力学模型，对其非线性动力响应进行进一步研究。

为揭示弹性地基梁的非线性动力学特性，本文基于弹性地基不可伸长梁的动力学模型，利用多尺度方法求得梁主共振响应的幅频响应方程和位移的二次近似解[14]，进而分析了弹性地基模型、边界条件、外激励幅值等参数对主共振响应的影响。

1 主共振响应(Ω≈ωn)

图1 弹性地基梁模型

图1为弹性地基梁模型。本文以弹性地基上长L，宽b，高h的有限长梁为研究对象。图1中：p为简谐荷载，p(x,t)=Pcos (Ωt)，P和Ω分别为外激励幅值和频率；q为地基反力，q(x,t)=k0v(x,t)-k1v″(x,t)，k0和k1分别为弹性地基的Winkler参数和剪切参数[12]；u(x,t)和v(x,t)分别为弹性地基梁沿x轴和y轴方向的位移。基于Hamilton原理，考虑不可伸长条件及土-结构相互作用效应，可得弹性地基上不可伸长梁的无量纲运动方程[12]：

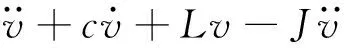
(1)

及边界条件：

x=0,1:v(x,t)v″(x,t)=0;v(x,t)v‴(x,t)=0;v′(x,t)v″(x,t)=0。

(2)

利用多尺度法[14]，弹性地基梁的位移v(x,t)可展开为：

(3)

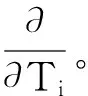
为研究主共振响应，需引入调谐参数σ，则外激励频率与弹性地基梁的固有频率间有如下关系：Ω=ωn+ε2σ，其中：ωn为弹性地基梁的第n阶频率[15]。为平衡非线性效应，将黏滞阻尼系数c和外激励幅值p调整为ε2c和ε3p。将式(3)代入调整后的式(1)，并按小参数ε的各阶系数调整结果，可得：

ε阶，

(4)

ε2阶，

(5)

ε3阶，

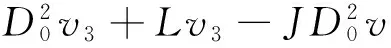
(6)

其中，各式均满足边界条件：

x=0,1:vi(x,T0,T2)v″i(x,T0,T2)=0，vi(x,T0,T2)v‴i(x,T0,T2)=0;

(7)

对于弹性地基梁第n阶模态的主共振响应而言，式(4)的解为：

v1(x,T0,T2)=An(T2)eiωnT0φn(x)+cc,

(8)

将式(8)代入式(5)，可得：

(9)

(10)

其中：Ψ1n和Ψ2n均为二阶构型函数，且满足下列公式：

(11)

将式(8)和式(10)代入式(6)，可得：

(12)

其中：NST表示非久期项。

由式(12)中的久期项得到可解性条件：

(13)

令响应幅值An为：

(14)

其中：an和βn均为T2的实函数。将式(14)代入式(13)，并分离实部与虚部，可得：

(15)

(16)

(17)

将式(8)和式(10)代入式(3)，可得弹性地基梁位移v(x,t)的二阶近似表达式：

(18)

其中：已令小参数ε=1。由式(18)可知：弹性地基梁位移的二阶近似表达式中含有稳定的漂移项：

(19)

2 数值分析

文献[12]研究表明：若充分考虑土-结构相互作用效应在弹性地基梁非线性动力响应中的贡献，则梁的主共振响应可能出现动力软化现象。因此，有必要对弹性地基梁的非线性动力响应进行进一步的深入分析。在后续的数值分析中，梁和地基的物理参数取值如表1所示。本文分别以弹性地基上铰支-自由梁 (H-F)和自由-自由梁(F-F)为对象，以其主共振响应为例进行研究。

表1 弹性地基和不可伸长梁的物理参数值

2.1 地基模型

图2给出了外激励幅值p=0.13时，不同弹性地基模型支承梁的主共振幅频响应曲线。图2a和图2b分别为铰支-自由梁和自由-自由梁的主共振响应情况，图2c则对比了弹性地基模型和边界条件共同作用下梁的主共振响应特性。由图2a可知：虽然弹性地基物理参数相同，但地基模型不同导致计算出的剪切参数不同，将引起弹性地基梁的主共振响应间存在一定差异。而且，弹性地基剪切参数引起主共振响应幅值及多值区域发生变化。但总体上讲，不同弹性地基支承梁的幅频响应曲线构型类似，均表现出明显的非线性软化特性。

由图2b可知：梁端边界条件放松引起梁主共振响应幅值及多值区域的显著改变，对称约束时主共振响应的多值区域更宽但幅值更小。而且还应注意到，三参数模型(Kerr)中弹性层对梁的动力响应幅值有更显著的增强作用。对比图2c中的骨架曲线可知：随着边界约束的放松，弹性地基梁主共振响应的动力软化特性增强。而且，弹性地基剪切参数对梁动力学特性的影响效应与边界条件密切相关。

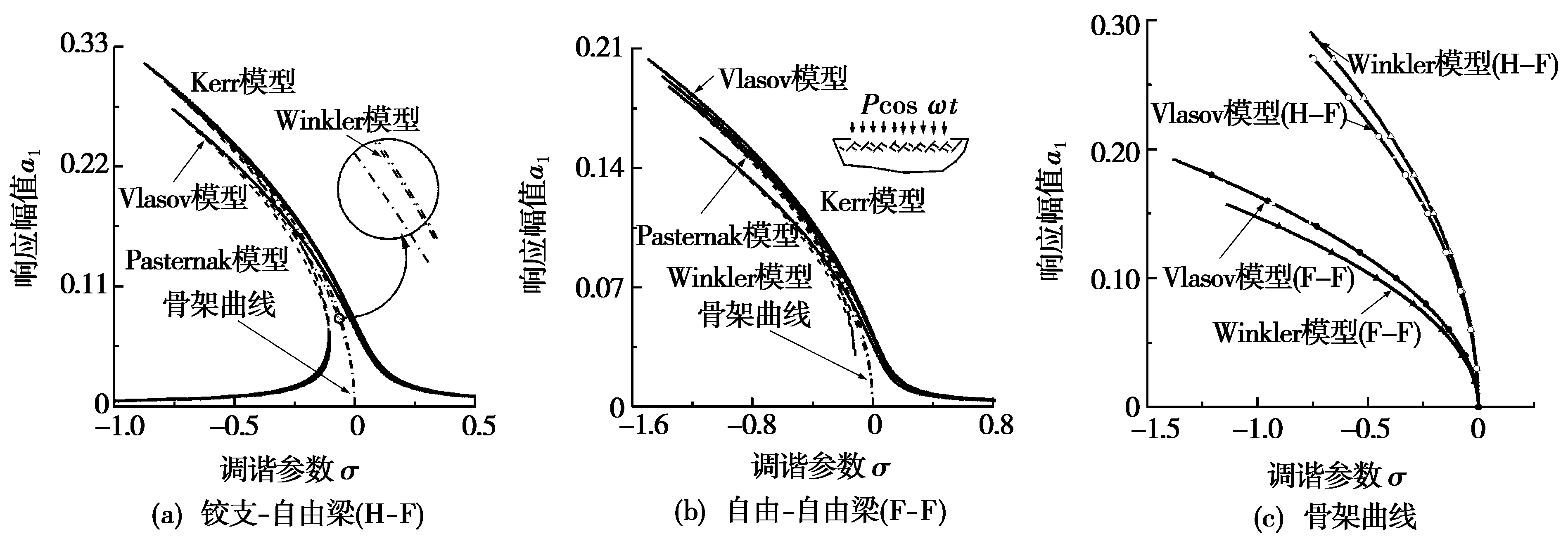
图2 不同弹性地基上梁的主共振幅频响应曲线(p=0.13)

2.2 Winkler参数

在弹性地基剪切参数K1=50和外激励幅值p=0.13时，为研究弹性地基Winkler参数k0对梁主共振响应的影响，图3a～图3c分别给出了铰支-自由梁和自由-自由梁的幅频响应曲线及骨架曲线。由图3a可知：弹性地基Winkler参数的增大导致弹性地基梁系统整体刚度增大，使得外激励难以激发系统的动力响应，相应的动力响应幅值也减小。在幅频响应曲线上选取调谐参数相同时的a、b、c三点，观察其对应的漂移量可知：Winkler参数的增加在抑制幅值的同时会减小稳定的漂移量。由图3b可知：梁端约束为自由-自由时，其幅频响应曲线与铰支-自由梁相类似，但边界约束放松导致系统共振区域变宽且幅值减小。同时，对比图3c中的骨架曲线可知：边界条件的改变将引起系统动力响应幅值和非线性软化特性的改变。边界约束的放松，在一定程度上增加了弹性地基Winkler参数对系统动力响应的影响。

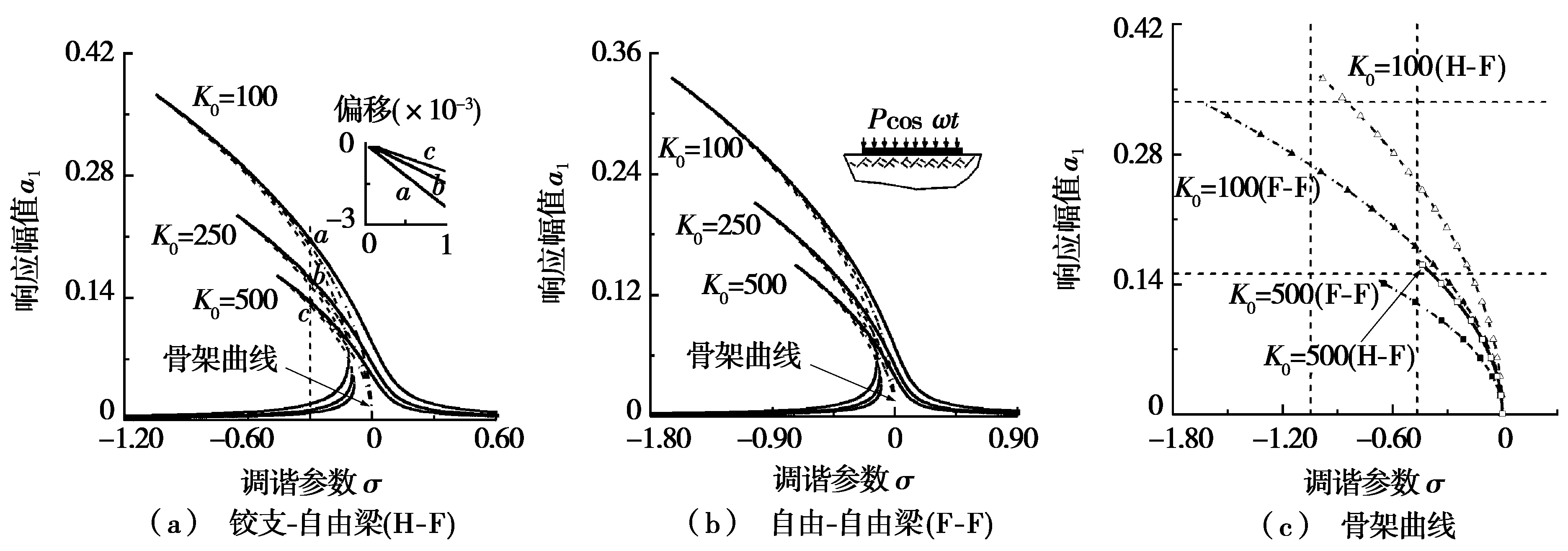
图3 弹性地基梁在p=0.13时的主共振幅频响应曲线

2.3 外激励幅值

在弹性地基参数为K0=500，K1=50时，图4a和图4b分别给出了弹性地基铰支-自由梁和自由-自由梁的主共振幅频响应曲线。理论上讲，外激励幅值与弹性地基梁的非线性动力学特性无关。如图4a和图4b所示，在相同边界条件时弹性地基梁主共振幅频响应的骨架曲线一致。由图4a可知：外激励幅值对主共振响应的幅值和多值区域均有明显影响，强激励对应高响应幅值和较宽的多值区域。对比图4a和图4b可知：梁端为对称约束时，弹性地基梁主共振响应的幅值较小。而且，边界约束对梁动力响应的漂移量有显著影响，例如对于自由-自由梁而言，梁左端的位移漂移量并不为0。

图4 弹性地基梁在K0=500时的主共振幅频响应曲线

3 结论

本文对弹性地基上不可伸长梁的主共振响应进行了研究，基于已建立的弹性地基梁动力学模型，运用多尺度方法求得梁主共振的幅频响应方程和位移的二次近似解，进而利用幅频响应曲线对其动力响应进行参数分析。研究结果表明：弹性地基模型对梁主共振响应的幅值及动力软化特性均有显著影响，应在系统的动力响应中对地基进行精细模拟；梁端约束通过对动力学构型的影响，改变了系统的动力学特性，同时导致弹性地基参数对系统动力学特性的作用效应发生变化。总体而言，考虑剪切效应的地基模型能更精确地揭示弹性地基上梁的动力学特性。

[1] Hetenyi M.Beams on Elastic Foundation[M].Ann Arbor:University of Michigan Press,1946.

[2] Timoshenko S.Vibration Problems in Engineering[M].2 ed.New York:Wolfenden Press,2008.

[3]Lai Y C,Ting B Y,Lee W S,et al.Dynamic Response of Beams on Elastic Foundation[J].Journal of Structural Engineering-ASCE,1992,118(3):853-858.

[4] Thambiratnam D,Zhuge Y.Free Vibration Analysis of Beams on Elastic Foundation[J].Computers & Structures,1996,60(6):971-980.

[5] 陈启勇,胡少伟,张子明.基于声子晶体理论的弹性地基梁的振动特性研究[J].应用数学和力学,2014,35(1):29-38.

[6]Wang Y H,Tham L G,Cheung Y K.Beams and Plates on Elastic Foundations:A Review[J].Progress in Structural Engineering and Materials,2005(7):174-182.

[7] 丁敏,李潇,马倩,等.基于Winkler弹性地基梁模型的半刚性轻钢柱脚底板受力分析[J].工程力学,2014,31(5):158-165.

[8] 何翊武,傅鹤林,罗立峰,等.隧底岩溶洞对结构稳定影响的理论解[J].土木工程学报,2014,47(10):128-135.

[9] Pellicano F,Mastroddi F.Nonlinear Dynamics of a Beam on Elastic Foundation[J].Nonlinear Dynamics,1997,14(4):335-355.

[10] 杨志安,赵雪娟,席晓燕.非线性弹性地基上矩形薄板的非线性振动与奇异性分析[J].振动与冲击,2006,25(5):69-73.

[11] 丁兰,朱宏平.移动荷载下黏弹性地基梁临界速度及瞬态响应[J].华中科技大学学报:自然科学版,2014,42(9):88-92.

[12] 马建军,王连华,赵跃宇.弹性地基有限长梁的动力学建模[J].中国科学:物理学力学天文学,2013,43:765-771.

[13] Manna B,Baidya D K.Nonlinear Dynamic Response of Piles Under Horizontal Excitation[J].Journal of Geotechnical and Geoenvironmental Engineering-ASCE,2010,136(12):1600-1609.

[14] Nayfeh A H,Mook D T.Nonlinear Oscillations[M].New York:Wiley,1979.

[15] Nayfeh A H,Pai P F.Linear and Nonlinear Structural Mechanics[M].New York:Wiley-Interscience,2004.

国家自然科学基金项目(51474095);河南省教育厅科学技术研究重点基金项目(14A410003);河南科技大学科研创新能力培育基金项目(2014ZCX005)

马建军(1982-),男,河南孟州人,讲师,博士,主要从事桩基非线性动力响应方面的研究.

2015-04-03

1672-6871(2015)06-0046-05

TU348；O322

A