相邻分体式路段人行横道的协调信号配时优化*

徐洪峰 何龙 章琨

(大连理工大学 交通运输学院， 辽宁 大连 116024)



相邻分体式路段人行横道的协调信号配时优化*

徐洪峰 何龙 章琨

(大连理工大学 交通运输学院， 辽宁 大连 116024)

人行横道是一种重要的行人过街设施.一体式人行横道适宜实施同步二次过街控制，分体式人行横道适宜实施独立二次过街控制.文中对于单个分体式路段信号控制人行横道，根据行人的时间距离关系，建立了行人最大过街时间计算方法.对于城市干道沿线的相邻分体式路段信号控制人行横道，根据机动车的时间距离关系，在保证机动车双向绿波效果的前提下，以最小化任意人行横道、任意步行方向的行人最大过街时间的最大值为目标，采用整数非线性规划方法，建立了协调信号配时优化模型.算例分析结果表明，该模型具有良好的实用性和广泛的适用性.

交通运输工程；路段人行横道；协调信号控制；整数非线性规划

人行过街设施包括平面过街设施和立体过街设施.人行横道是最为常见的平面过街设施，通常设置于交叉口和路段.当城市干道沿线的信号控制交叉口相距较远时，应在行人过街需求相对集中的地点设置路段人行横道[1].为了规范交通运行秩序、减少交通事故隐患，宜对机动车交通量和(或)行人交通量较大的路段人行横道实施交通信号控制.在城市商业区和居住区，干道沿线存在连续多个路段信号控制人行横道的情形具有一定的普遍性.

普通信号控制交叉口处，通行权的竞争主体是机动车，行人可以在机动车的“保护”下享有通行权，信号配时方法以优化机动车的通行利益为基本目的，以机动车的通行时间资源需求(即流率比)为主要计算依据，以行人的通行时间资源需求(即行人过街时间)为约束条件之一[2].

路段信号控制人行横道处，通行权的竞争主体是机动车和行人，信号配时方法以优化机动车和行人的通行利益为基本目的，以机动车和行人的通行时间资源需求为计算依据.但是，由于机动车与行人的交通运行特性不同[3]，它们的通行时间资源需求的描述方式也不同，普通信号控制交叉口的信号配时方法无法应用于路段信号控制人行横道.为此，一些学者尝试建立了适用于路段信号控制人行横道的信号配时方法[4- 7].

以往涉及路段人行横道的协调信号控制方法的研究，多以路段人行横道及其相邻的交叉口为研究对象[8- 11].对于相邻路段信号控制人行横道的协调信号配时问题，通常采用相邻普通信号控制交叉口的协调信号配时方法进行建模和求解[12- 13].然而，行人过街安全岛的设置给路段信号控制人行横道的道路空间布局和交通运行组织带来了新的变化，它们为创新相邻路段信号控制人行横道的协调信号配时方法创造了机遇，有必要在此背景下开展相关研究工作.需要说明的是，本文将重点关注分体式路段信号控制人行横道对于机动车和行人的通行效率的影响，对于机动车和行人的交通安全的影响不做深入讨论.

1 符号解释

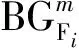
2 道路空间布局

根据《城市道路交叉口规划规范》的要求，人行横道长度超过16 m时(不包括非机动车道)，应在人行横道中央规划设置宽度不小于1.5 m的行人过街安全岛[14].设置行人过街安全岛的主要目的包括：①面向未能在一次绿灯时间内完成过街的行人提供安全的驻足等待空间；②便于实施行人二次过街控制.

设置行人过街安全岛后，整条人行横道被分为两段.从道路空间布局的角度，将人行横道分为两种形式[15]：①一体式，即行人能够在不改变步行方向的情况下通过整条人行横道，如图1(a)所示；②分体式，即行人通过第一段人行横道后，必须在安全岛上改变步行方向，方能通过另一段人行横道，如图1(b)所示.与一体式人行横道相比，分体式人行横道的步行距离较长，机动车停止线间距和安全岛面积均较大，同时，安全岛的边缘应设置实体隔离栏，以防止行人违规穿越机动车道.

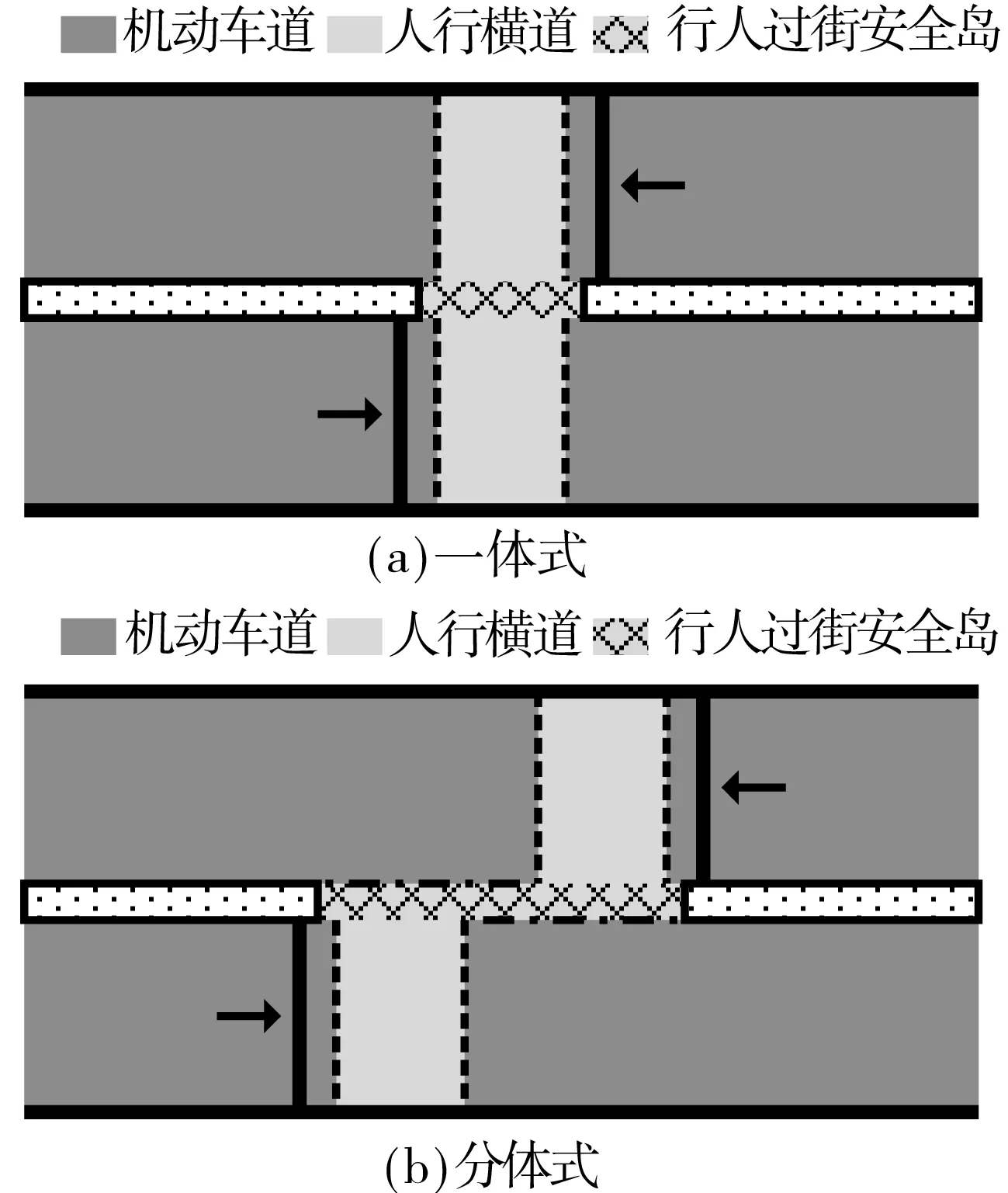
图1 路段人行横道布局

3 交通运行组织

行人二次过街是指信号控制人行横道两端的行人至多需要获得两次通行权即能通过整条人行横道的交通组织方式.对于具有行人过街安全岛的路段信号控制人行横道，除布设2组机动车信号灯之外，还应在人行横道两端布设2组行人信号灯、在行人过街安全岛上布设2组行人信号灯，从而实施同步二次过街控制或独立二次过街控制[16].

同步二次过街控制旨在使得人行横道两端的行人快速通过整条人行横道.4组行人信号灯归属于同一行人相位(F1)，2组机动车信号灯归属于同一机动车相位(K1).不允许机动车相位和行人相位同时获得通行权.一体式人行横道的步行距离短，适宜实施同步二次过街控制.机动车和行人的交通运行方式，如图2(a)所示.

独立二次过街控制旨在充分利用安全岛积蓄行人、灵活调节机动车和行人的通行时间资源供求关系.安全岛一侧的2组行人信号灯和另一侧的2组行人信号灯归属于不同的行人相位(F1、F2)，2组机动车信号灯归属于不同的机动车相位(K1、K2).相位K1与相位K2或F2同步获得通行权；相位K2与相位K1或F1同步获得通行权；一旦切断相位K1(或F1)的绿灯时间，相位F1(或K1)将获得通行权；一旦切断相位K2(或F2)的绿灯时间，相位F2(或K2)将获得通行权.分体式人行横道的安全岛面积大，适宜实施独立二次过街控制.机动车和行人的交通运行方式，如图2(b)所示.

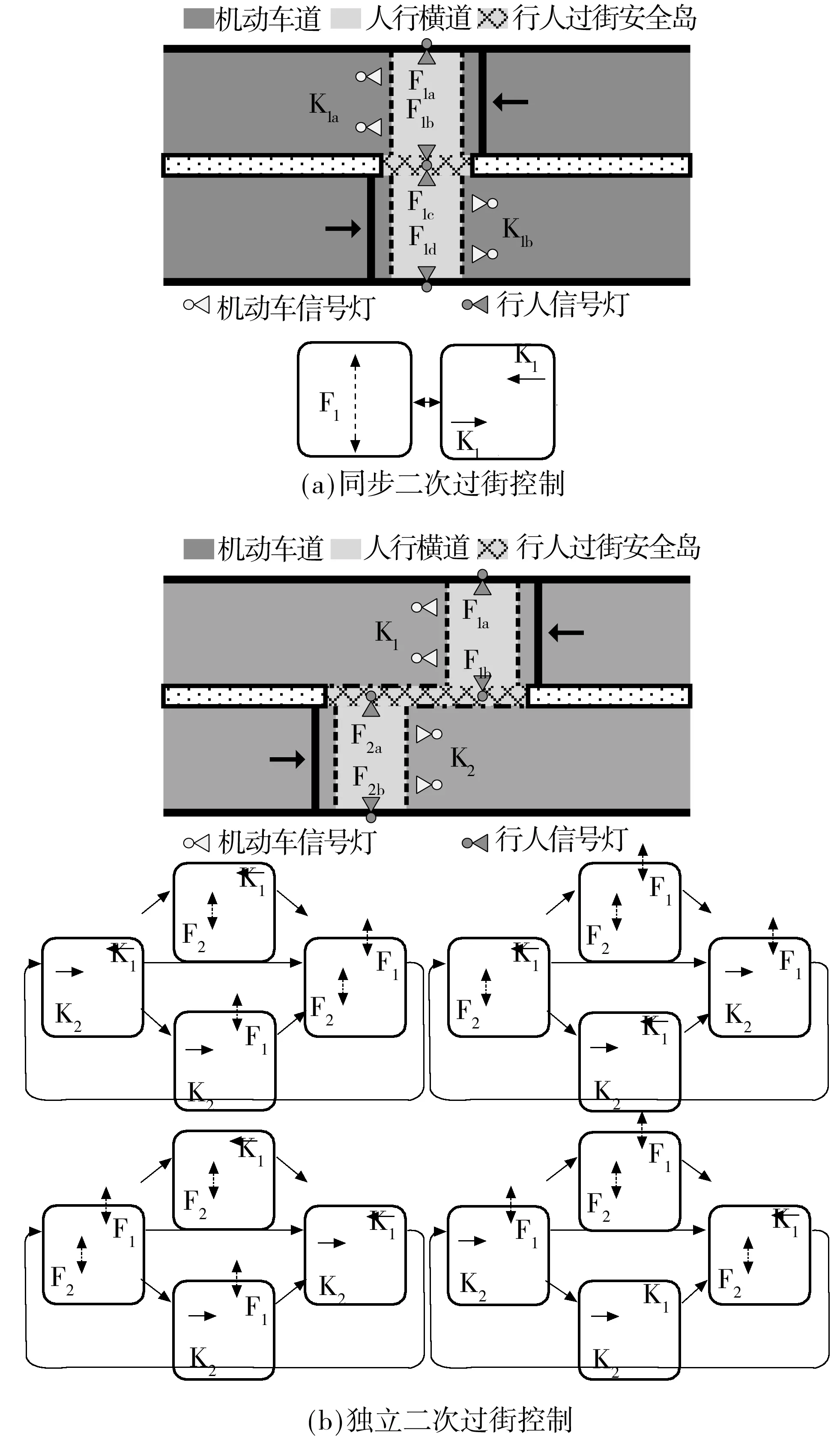
图2 交通运行方式

4 行人最大过街时间

行人最大过街时间是指人行横道一端的行人自到达人行横道边缘至通过整条人行横道所需的时间，是衡量分体式信号控制人行横道的行人过街舒适度的重要指标.行人最大过街时间包括人行横道边缘的等待时间、第1段人行横道的步行时间、安全岛的步行时间、安全岛边缘的等待时间和第2段人行横道的步行时间.1条人行横道具有2个步行方向，因此，具有2个行人最大过街时间.

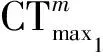
(a)情形1：绿灯初期进入人行横道的行人须在安全岛上等待

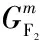
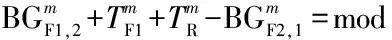
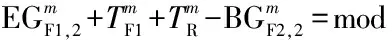
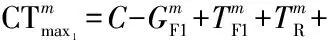
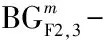
(b)情形2：绿灯初期和末期进入人行横道的行人须在安全岛上等待

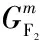
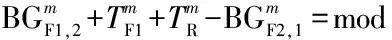
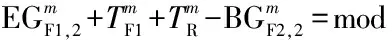
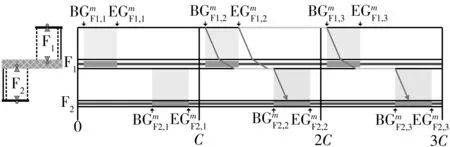
(c)情形3：绿灯期间进入人行横道的行人须在安全岛上等待

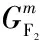
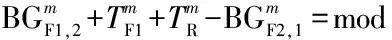
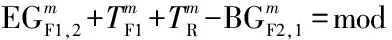
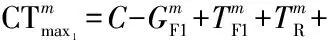
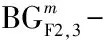
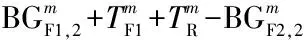
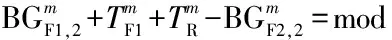
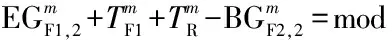
(e)情形5：绿灯末期进入人行横道的行人须在安全岛上等待

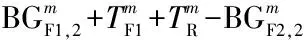
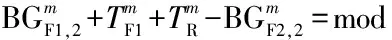
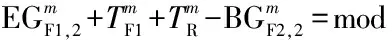
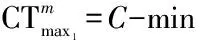
(f)情形6：绿灯中期进入人行横道的行人须在安全岛上等待

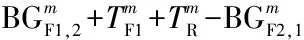
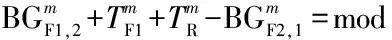
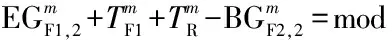
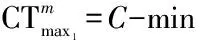
图3 步行方向1的时间距离关系

Fig.3 Time-space diagram of pedestrian movement 1

(a)情形1：绿灯初期进入人行横道的行人须在安全岛上等待

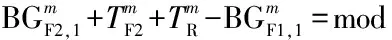
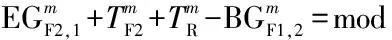
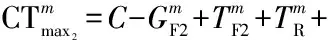
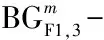
(b)情形2：绿灯初期和末期进入人行横道的行人须在安全岛上等待

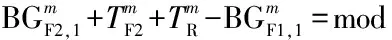
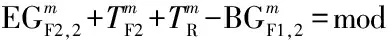
(c)情形3：绿灯期间进入人行横道的行人须在安全岛上等待

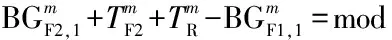
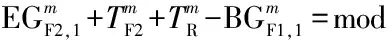
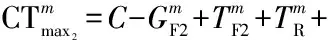
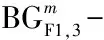
(d)情形4：绿灯期间进入人行横道的行人无须在安全岛上等待

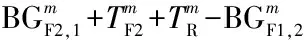
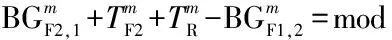
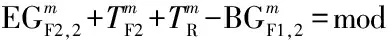
(e)情形5：绿灯末期进入人行横道的行人须在安全岛上等待

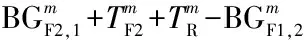
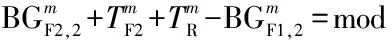
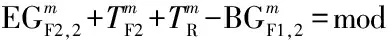
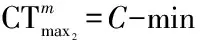
(f)情形6：绿灯中期进入人行横道的行人须在安全岛上等待

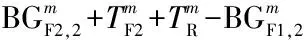
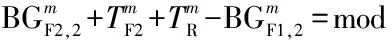
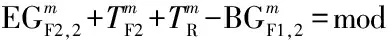
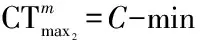
图4 步行方向2的时间距离关系

Fig.4 Time-space diagram of pedestrian movement 2

(1)

(2)

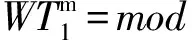
(3)

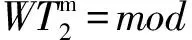
(4)

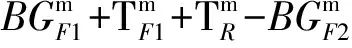
(5)

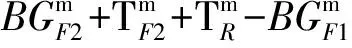
(6)

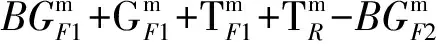
(7)

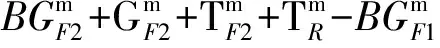
(8)

5 协调信号配时优化模型

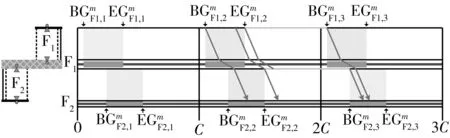
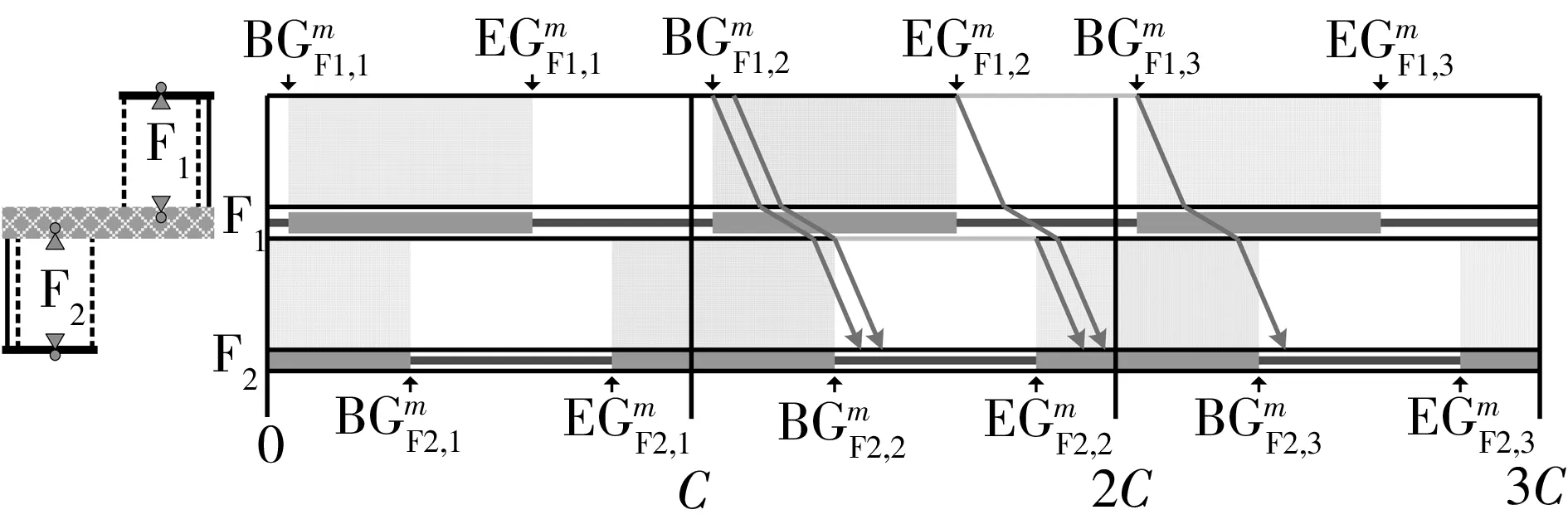
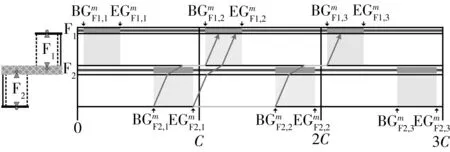
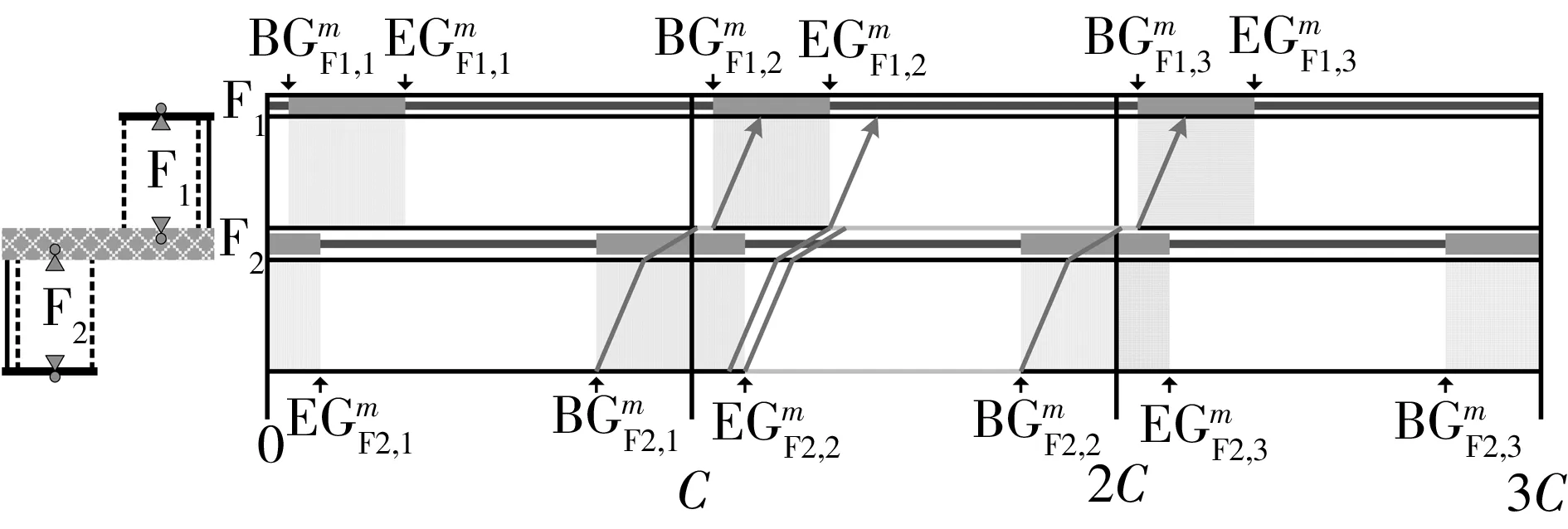
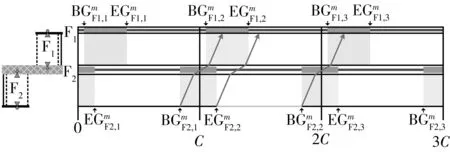
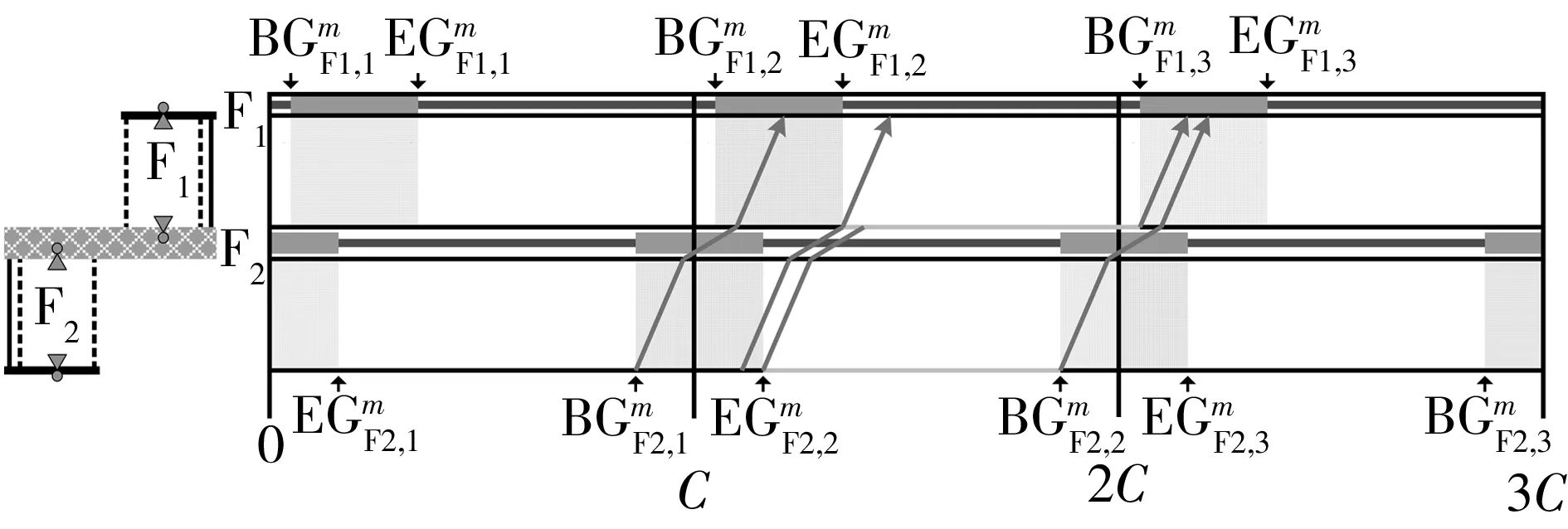
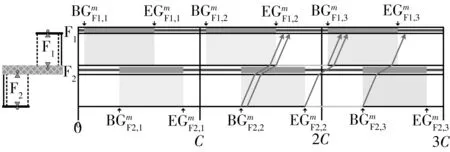
以2个相邻的分体式路段信号控制人行横道为研究对象(如图5所示)，在保证机动车双向绿波效果的前提下，以最小化任意人行横道、任意步行方向的行人最大过街时间的最大值为目标，采用整数非线性规划方法，建立一种协调信号配时优化模型，如式(9)所示.

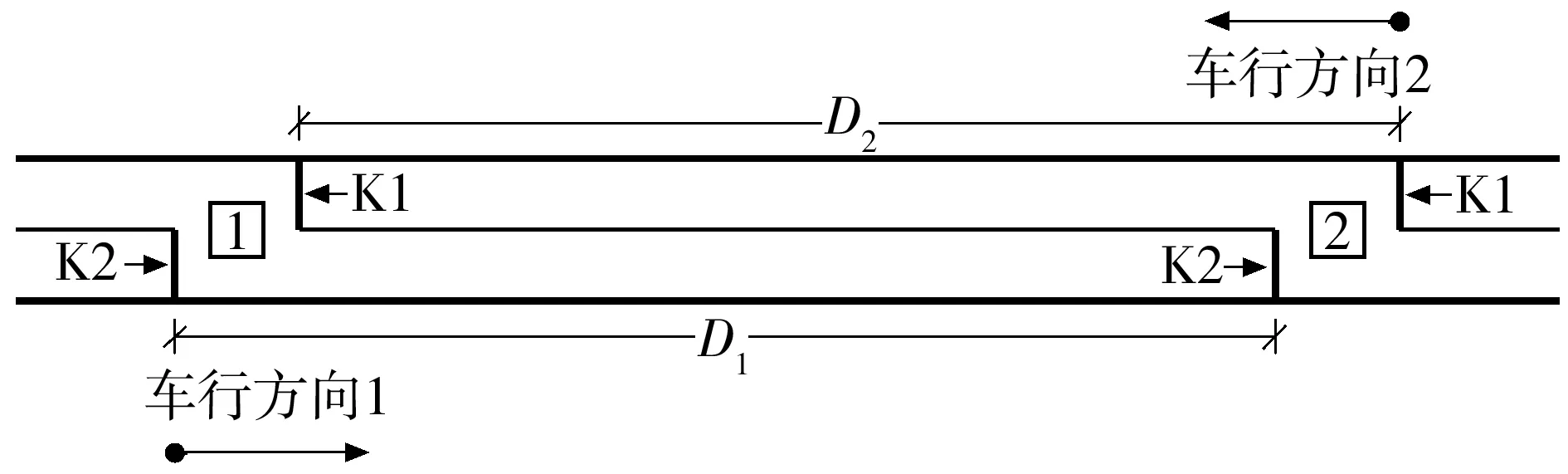
图5 对象路段

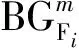
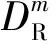
(9)

决策变量除了受到最大公共信号周期时间(条件1)、机动车相位的最小绿灯时间(条件2)、机动车相位的设计饱和度(条件3)的约束外，还将受到以下条件的约束：

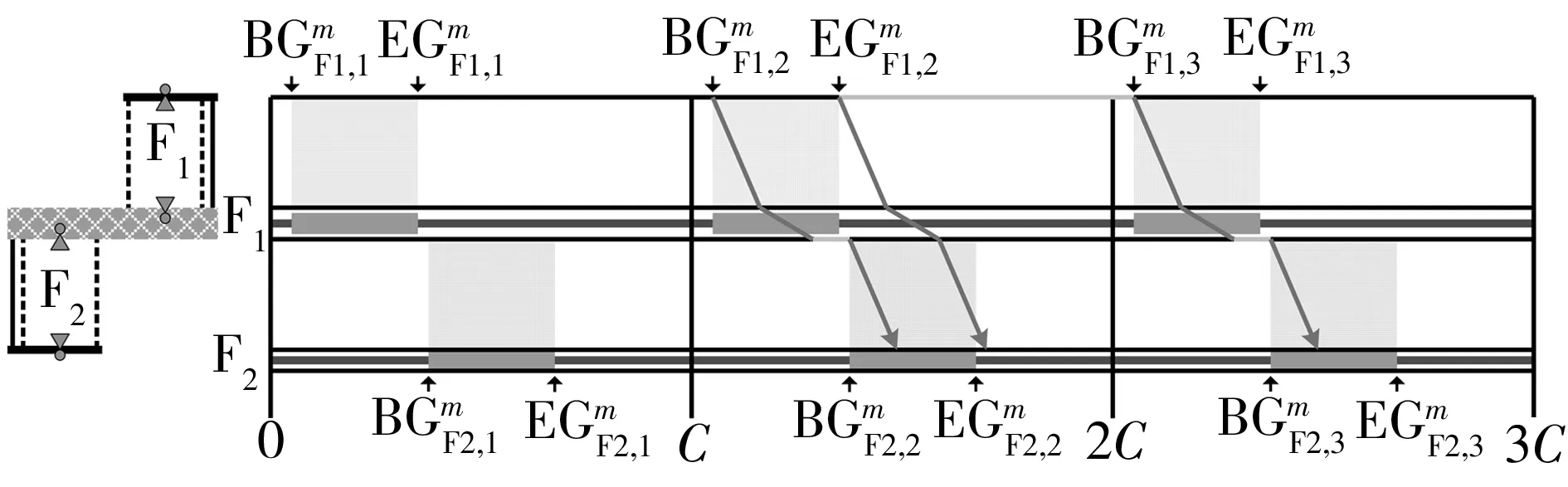
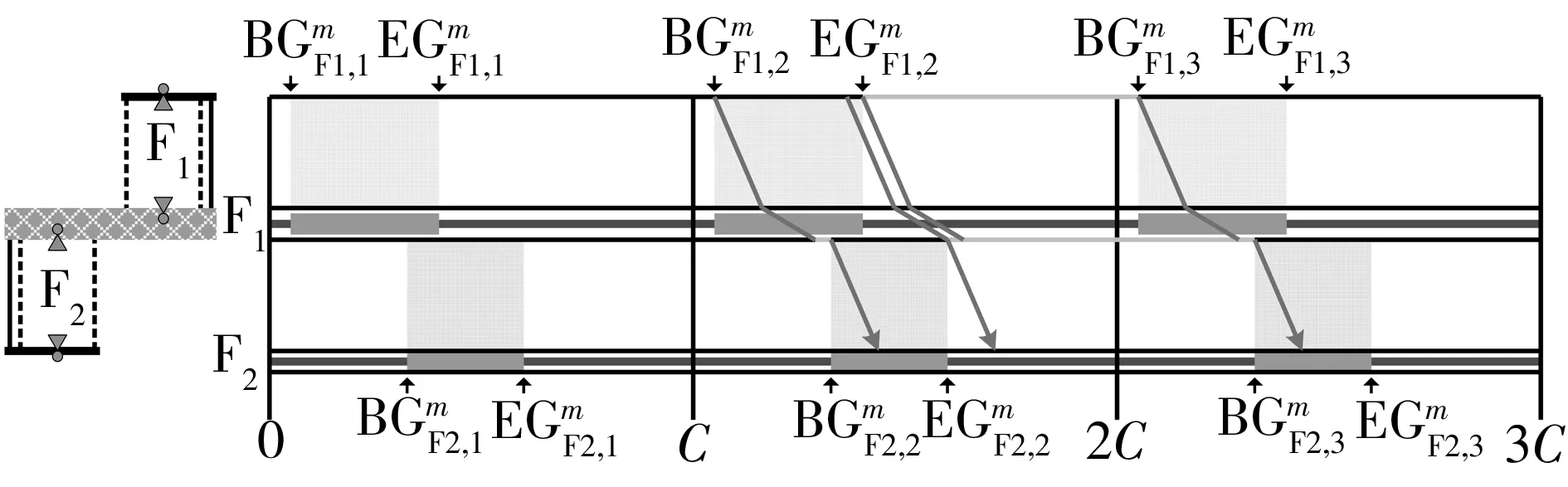
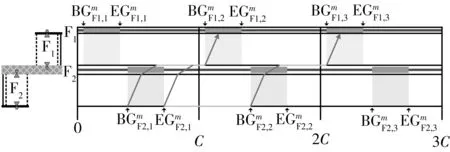
下游协调相位的初始排队消散时间边界值(条件4)：以车行方向1为例，根据机动车的时间距离关系(如图6所示)，若上游协调相位的车队头车在到达下游协调相位的停止线之前受到红灯期间排队车辆的阻滞而减速停车，紧随车队头车的后续车辆将减速停车或缓行，远离车队头车的后续车辆可能以设计车速行驶并顺利通过下游协调相位的停止线.因此，在上游协调相位的车队头车到达下游协调相位的停止线之前，保证下游协调相位具有一定的初始排队消散时间是形成机动车绿波效果的重要前提.

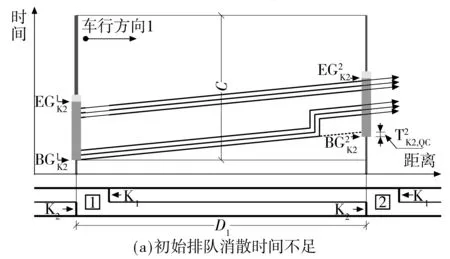
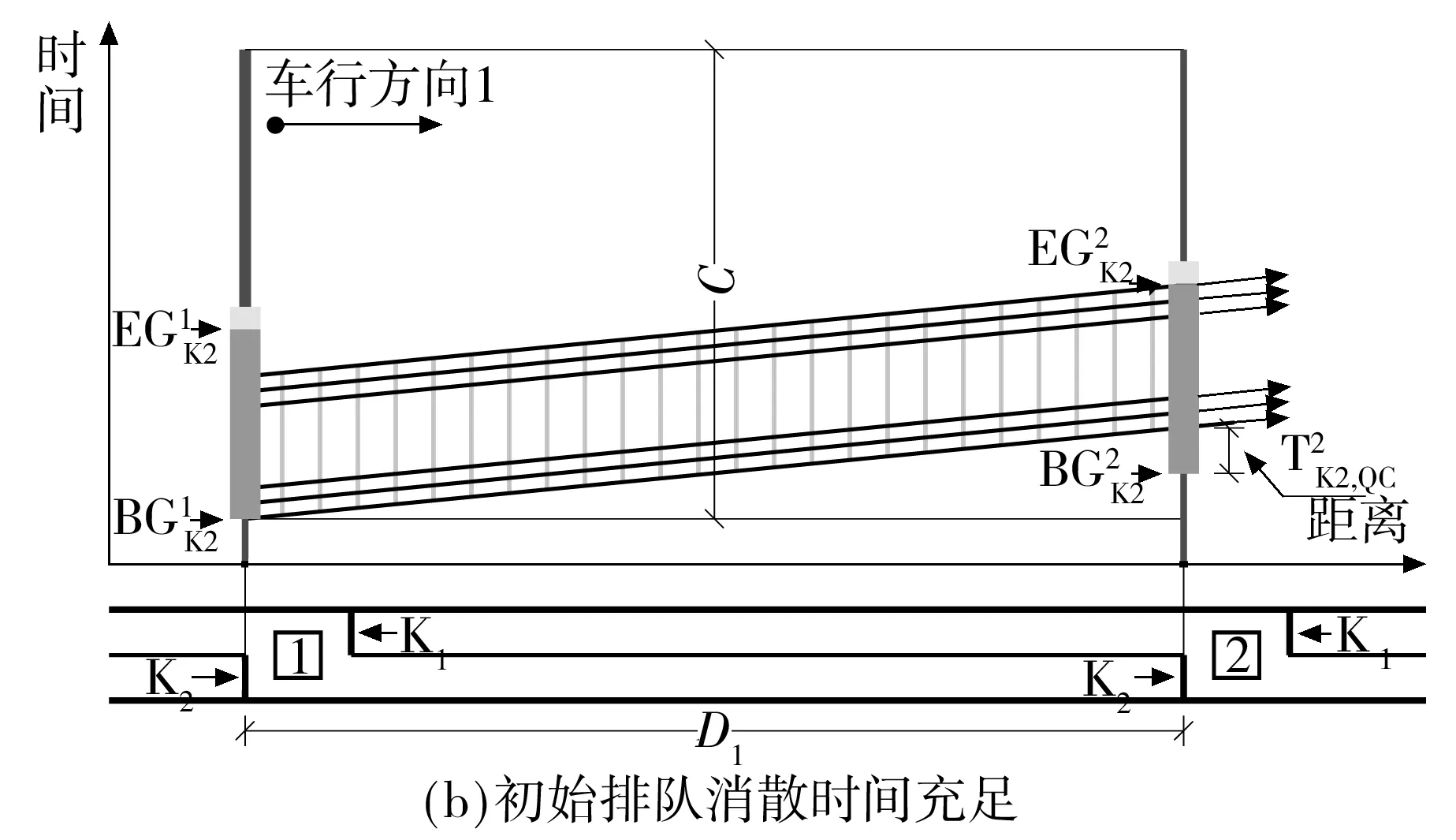
图6 任意车行方向的时间距离关系

最小绿波带宽率(条件5)：绿波带宽率，即任意车行方向的绿波带宽与上游协调相位的绿灯时间的比值.在下游协调相位具有一定的初始排队消散时间的前提下，绿波带宽等于下游协调相位的绿灯结束时刻减去上游协调相位的车队头车以设计车速行进至下游协调相位停止线的时刻.主要车行方向的绿波带宽率应大于等于次要车行方向.

条件6、7、8、9、10分别给出了下游协调相位的初始排队消散时间、绿波带宽率、安全岛的步行时间、机动车停止线之间的设计行程时间、机动车相位的绿灯时间、机动车相位和行人相位的绿灯启亮时刻等信号配时参数的计算方法；条件11-14是对研究对象和建模假设的体现.

6 算例分析

某一双向通行的城市主干道具有6条机动车道，拟在道路沿线的一定距离内设置2处路段信号控制人行横道，备选的道路空间布局形式包括分体式人行横道和一体式人行横道.车行方向1为机动车的主要方向(见图5).

道路空间条件包括：

①D1=D2=100,150,200,250,300 m；

交通需求条件包括：

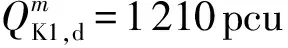
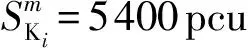
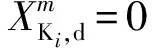
④VP,d=1.2 m/s，VV,d=50 km/h；

⑤BEmin1=0.7，BEmin2=0.4.

分体式人行横道的信号控制条件包括：

①采用独立二次过街控制；

②Cmax=100 s；

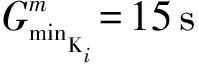
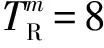
⑤TT1=TT2=7.2,10.8,14.4,18,21.6 s;

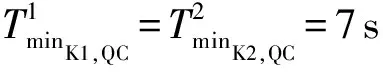
⑦intg(Ki,Fi)m=5 s，intg(Fi,Ki)m=9 s；

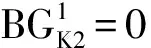
一体式人行横道的信号控制条件包括：

①采用同步二次过街控制；

②采用与分体式人行横道相同的信号周期时间；

③采用与分体式人行横道相同的机动车相位绿灯时间和行人相位绿灯时间；

④车行方向1采用与分体式人行横道相同的绿波带宽率；

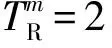
⑥其他信号配时参数均与分体式人行横道相同.

利用LINGO求解相邻分体式路段信号控制人行横道的协调信号配时优化模型.利用时间距离图求解相邻一体式路段信号控制人行横道的行人最大过街时间和车行方向2的绿波带宽率.最终得到的协调信号配时方案，如表1所示.

当相邻路段信号控制人行横道的间距较近(如100 m、150 m)时，与一体式人行横道相比，分体式人行横道无法改善机动车的双向绿波效果，同时，将产生较大的行人最大过街时间；随着相邻路段信号控制人行横道间距的增大，尽管行人最大过街时间仍然处于较高水平，但是，分体式人行横道能够显著改善机动车的双向绿波效果.

表1 协调信号配时方案

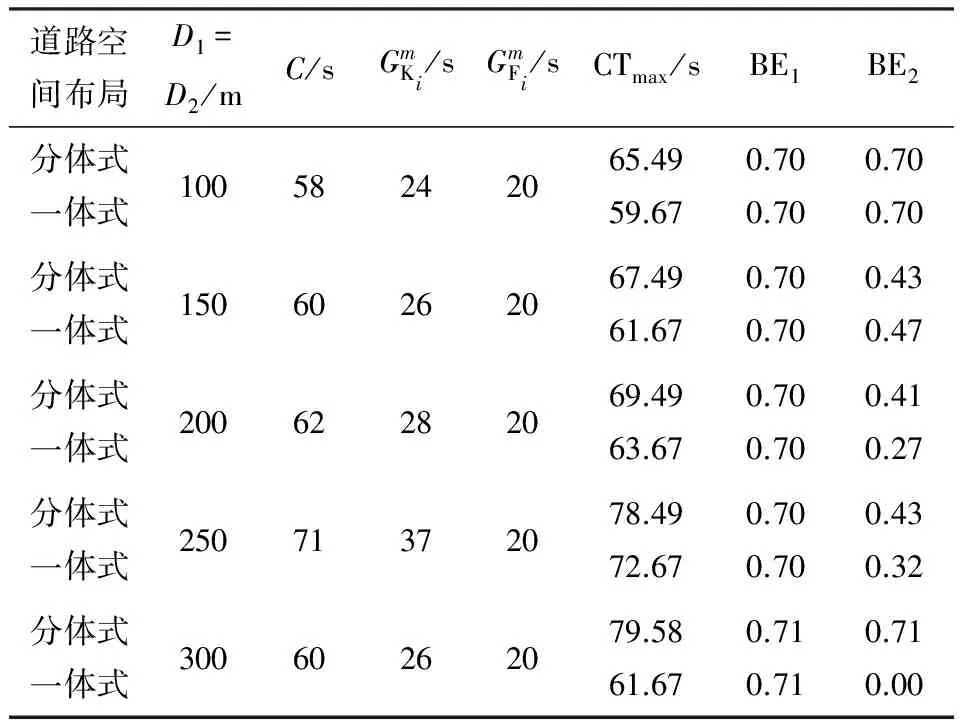
Table 1 Coordinated signal timing plans

7 结论

分体式路段信号控制人行横道可以为机动车和行人提供更加多样的交通运行方式，从而更加灵活地调节机动车和行人的通行时间资源供求关系.在城市干道沿线连续设置多个分体式路段信号控制人行横道，而非一体式路段信号控制人行横道，对于改善机动车的通行利益具有积极意义，但是，也将在一定程度上牺牲行人的通行利益.

对于相邻的分体式路段信号控制人行横道，采用整数非线性规划方法建立的协调信号配时优化模型，以行人和机动车的时间距离关系为基础，以保证机动车的双向绿波效果为前提，以缩短行人过街时间为目的，模型结构简单，待定参数少且易于确定.算例分析结果表明，该模型具有良好的实用性和广泛的适用性.

[1] 冯树民，李松龄，裴玉龙.基于交通效益的路段无控制人行横道设置 [J].哈尔滨工业大学学报，2009，41(7):73- 77. Feng Shu-min，Li Song-ling，Pei Yu-long.Setting of uncontrolled crosswalk on road section based on traffic benefit [J].Journal of Harbin Institute of Technology，2009，41(7):73- 77.

[2] Akcelik R.Traffic signals:capacity and timing analysis [R].Vermont South Victoria:ARRB Transport Research Ltd，1983.

[3] 王芳.无信号控制人行横道处行人交通流特性分析及实证应用 [D].长春：吉林大学交通学院，2007.

[4] Ma Wan-jing，Liu Yue，Xie Han-zhou，et al.Multiobjective optimization of signal timings for two-stage，midblock pedestrian crosswalk [J].Transportation Research Record，2011，2264:34- 43.

[5] Ma Wan-jing，Yang Xiao-guang，Pu Wen-jing，et al.Signal timing optimization models for two-stage midblock pedestrian crossing [J].Transportation Research Record，2010，2198:133- 144.

[6] 邹志云，周志浩，葛欢.路段人行横道信号优化设计 [J].交通运输系统工程与信息，2009，9(6):142- 147. Zou Zhi-yun，Zhou Zhi-hao，Ge Huan.Optimization of road section crosswalk signal design [J].Journal of Transportation Systems Engineering and Information Technology，2009，9(6):142- 147.

[7] 冯树民.路段人行横道信号控制优化 [J].交通运输系统工程与信息，2008，8(5):73- 76. Feng Shu-min.Signal control optimization for crosswalk on road section Coordination Control of crossing pedestian signaland crossroads signal [J].Journal of Transportation Systems Engineering and Information Technology，2008，8(5):73- 76.

[8] 郑长江，王炜，陈淑燕.行人过街信号与交叉口信号的协调控制 [J].交通运输工程学报，2004，4(4):106- 109. Zheng Chang-jiang，Wang Wei，Chen Shu-yan.Coordination control of crossing pedestrian signal and cross roads signal [J].Journal of Traffic and Transportation Engineering，2004，4(4):106- 109.

[9] 高帅和.行人过街的上下游信号交叉口协调控制方法研究 [J].辽宁省交通高等专科学校学报，2008，9(2):45- 47. Gao Shuai-he.Street pedestrian crossing on the downstream signal coordination itersection control method [J].Journal of Liaoning Provincial College of Communications，2008，9(2):45- 47.

[10] 郑长江.行人过街信号与交叉口信号联动控制方法研究 [D].南京：东南大学交通学院，2006.

[11] 李娜.路段行人过街信号与交叉口信号协调控制研究 [D].南京：东南大学交通学院，2004.

[12] 罗格,艾琳娜,威廉姆.交通工程(应用) [M].北京:机械工业出版社,2008.

[13] Koonce P，Lee R，Lee K，et al.Signal timing manual [R].Washington DC：Turner-Fairbank Highway Research Center，Federal Highway Administration，2008.

[14] GB 50647—2011，城市道路交叉口规划规范 [S].

[15] 郑明明，徐洪峰.路段信号控制人行横道的控制方案设计与分析 [J].交通与计算机，2006，24(2):137- 141. Zheng Ming-ming，Xu Hong-feng.Control systen design and analysis of the link signal control pedestrian crossing [J].Computer and Communications，2006，24(2):137- 141.

[16] 李克平.交通信号控制指南-德国现行规范(RiLSA) [M].北京:中国建筑工业出版社，2006.

Coordinated Signal Timing Optimization at Closely-Spaced Split Midblock Crosswalks

XuHong-fengHeLongZhangKun

(School of Transportation and Logistics, Dalian University of Technology, Dalian 116024, Liaoning, China)

Crosswalks are a kind of important pedestrian crossing facility. It is proper to implement the simultaneous signalization at integrated crosswalks and the separate signalization at split crosswalks. Regarding isolated split midblock crosswalks, a method to calculate the maximum pedestrian-crossing time is proposed according to the time-space diagram of pedestrian movements. Regarding closely-spaced split midblock crosswalks along an arterial, a coordinated signal timing optimization model is constructed by means of the integer nonlinear programming method according to the time-space diagram of vehicular movements. In the constructed model, the maximum of the maximum pedestrian-crossing time in any crosswalk and in any movement direction is minimized without any negative effect on the two-way green waves for vehicular movements. Case studies indicate that the constructed model is of practical value and can be widely applied.

transportation engineering; midblock crosswalk; coordinated signal control; integer nonlinear programming

2015- 02- 11

国家自然科学基金资助项目(61374193) Foundation item: Supported by the National Natural Science Foundation of China(61374193)

徐洪峰(1978-)，男，博士，副教授，主要从事交通组织、管理与控制研究.E-mail： hfxu@dlut.edu.cn

1000- 565X(2015)12- 0106- 08

U 491.2

10.3969/j.issn.1000-565X.2015.12.015