基于图论和改进模糊遗传算法的配电网转供方法*

武志刚 马义松

(华南理工大学 电力学院， 广东 广州 510640)



基于图论和改进模糊遗传算法的配电网转供方法*

武志刚 马义松

(华南理工大学 电力学院， 广东 广州 510640)

针对复杂配电网的故障恢复问题，提出一种基于图论和改进模糊遗传算法的配电网负荷转供判断方法.首先基于图形库JGraphT进行配电网数据建模，将馈线拓扑结构和元件参数整合在一起，显式地利用配电网拓扑结构，避免了繁琐的节点编码规则和冗杂的邻接表、矩阵存储模式; 基于JGraphT集成的图论算法实现快速的故障区域类型区分、网络拓扑约束判断,开发出基于图论递归运算的前推回代潮流算法；然后结合配电网特点提出改进的模糊遗传算法，动态调整遗传算法的初始解和遗传算子以提高算法寻优性能，通过对模糊输入量和模糊规则进行完善，提高遗传算法的收敛速度，避免不成熟收敛的发生；算例结果表明，文中算法在潮流计算效率和寻优效率方面均具有更好的效果.

JGraphT；负荷转供；配网潮流；遗传算法

负荷转供可以保证配电网的安全经济运行，提高供电可靠性，是配网自动化建设的核心内容之一.配电网发生故障后，调度人员应综合考虑各种约束条件，尽可能制定最优的故障恢复方案.

配电网故障恢复方案实际为开关操作策略，通过改变待转供区域的支路开关状态使网络拓扑和潮流方向改变，因此拓扑分析和潮流计算在故障恢复中不断被调以判断网络是否正常运行，是实现负荷转供的基础.配网潮流算法(如最常见的前推回代算法)通常需先对网络进行节点编号，确定各支路功率和节点电压的计算路径和计算顺序.文献[1]中在节点编号优化的基础上提出一种节点编号的新方法，但节点编号过程仍较为繁琐.在节点编号的基础上，配网拓扑分析通常采用邻接表或矩阵表示，文献[2]中通过构造邻接表保存配电网拓扑结构，但重用性较差，当网络结构或者网络参数发生变化时，则需重新计算以更新表参数，故此法不能及时得到其结构.文献[3- 4]采用矩阵表示配电网的分层，不能直接反映配网的拓扑关系，而且随着网络规模的增大，计算量成倍增长，占用内存大.

配电网故障恢复从数学角度来看是一个典型的多目标多约束问题，其优化目标包括负荷切除量最少、开关动作次数最少、转供后网损最小等，同时该优化目标需要满足线路潮流分布、配电网辐射状运行和供电质量等诸多约束.

国内学者对配电网供电恢复问题进行了大量研究，其中智能优化算法[5]得到了广泛应用.作为现代智能优化算法的典型代表，遗传算法(GA)因其优秀的全局搜索性能在配电网负荷转供问题中得到推广[6].遗传算法为模拟生物进化过程的计算模型，整体搜索性能良好并且不依赖梯度信息，但假如没有结合电力系统本身的特性，传统的遗传算法只是一个随机的寻优过程，存在着搜索范围大、迭代次数多和收敛速度慢的缺陷，不适用于大规模配电网的故障转供判断.文献[7]中采用遗传算法来分析地区电网停电恢复，取得了一定的成果，但为了计算速度的需求，所用优化模型过于简化.文献[8- 9]中提出通过模糊规则在线地改变交叉算子和变异算子，但模糊控制考虑的影响因素较为简单，作用有限.

针对上述问题，文中利用开源图形库JGraphT进行配电网数据建模，将馈线拓扑结构和元件参数整合在一起，显式地利用配电网拓扑结构，避免了繁琐的节点编码规则和冗杂的邻接表或矩阵存储模式.此外，文中结合电网特点提出改进的模糊遗传算法，动态调整遗传算法的初始解和遗传算子以提高算法寻优性能，提高收敛速度，避免不成熟收敛的发生.

1 基于JGraphT的配电网数据建模

1.1 图形库JGraphT

JGraphT[10]是基于Java的开源图形库，提供数学图论中的对象和算法.JGraphT支持无向图或有向图、加权图或非加权图等对象，并提供连通性检查、最短路径获取等图论算法,另外JGraphT几乎涉及了所有对图这一数据结构的操作，包括图的创建、删除、修改、遍历和显示等需求.JGraphT中图的顶点支持任何数据格式，因此图形可以基于Strings、URLs、XML文档等不同类型数据创建.

1.2 配电网数据建模

研究故障转供需要提供配电网相关的基础参数和运行数据.文中基于配电网中存在的不同元件类型，基于JGraphT定义相应的类对象，配电网建模的整体结构如图1所示.

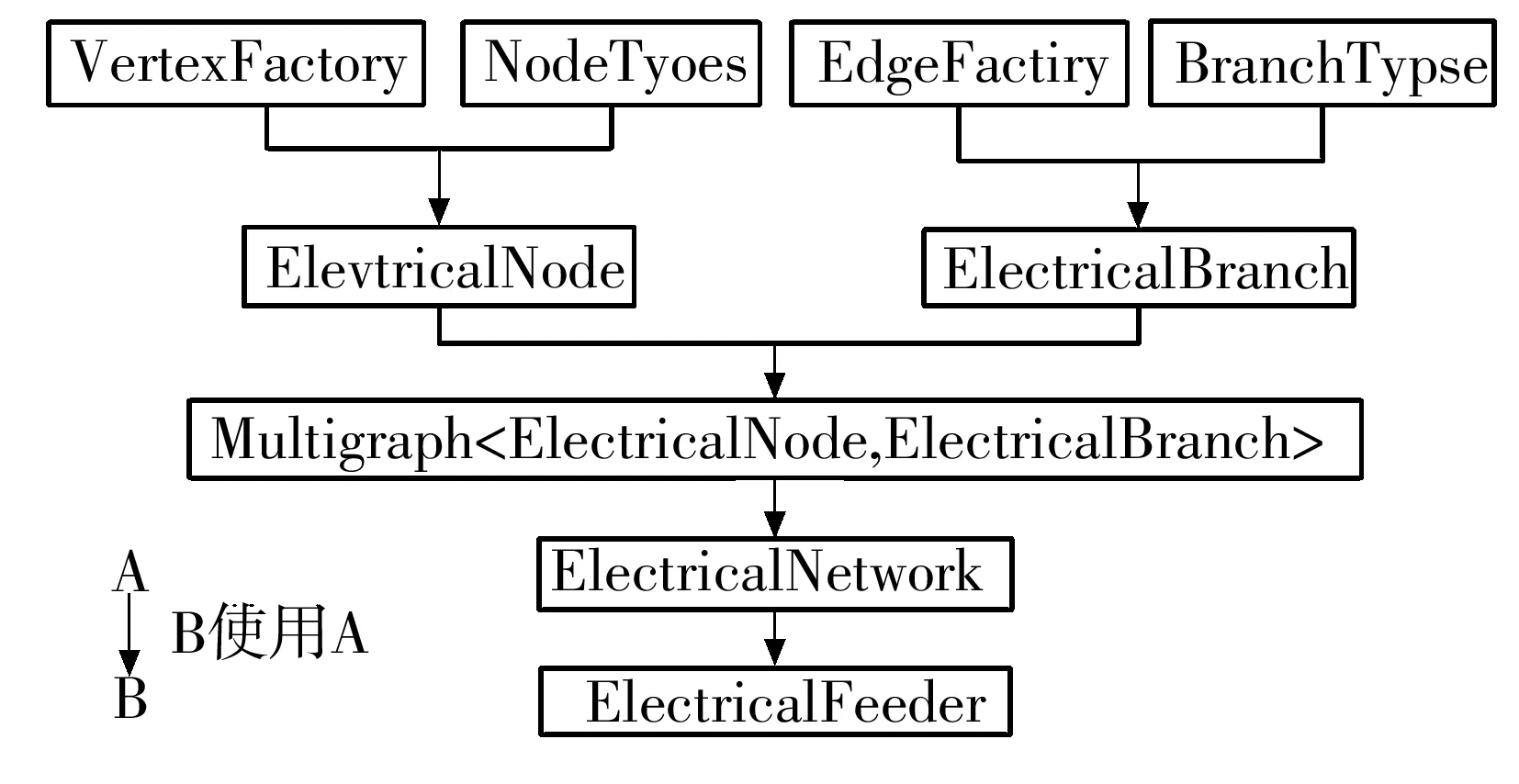
图1 基于JGraphT的配电网建模

根元素EdgeFactory、VertexFactory分别为JGraphT中节点和边的基类，根元素NodeTypes、BranchTypes分别定义了配电网中的节点类型和支路类型，例如BranchTypes包括交流输电线路、变压器、联络线等支路类型.ElectricalNode和ElectricalBranch为定义的配电网元件基本类，ElectricalNetwork为继承类Multigraph的通用电力网络类，显示包含了配电网完整的网络拓扑结构.ElectricalFeeder类为ElectricalNetwork电力网络类的某一个具体子类，即馈线，除具有电力网络中的所有属性和功能外，还添加了馈线特有的特性，例如所有馈线均有且只有一个电源节点，正常运行的馈线均为开式网络(解环，树状拓扑).

1.3 故障影响区域类型划分

当节点发生故障后，断路器保护跳闸，动作断路器后向的节点不受故障影响，而该断路器前向的节点均为受影响节点，故障后需要断开相应的隔离开关将故障隔离，执行该隔离操作的开关称为边界开关.针对受故障影响程度的不同，定义了3种故障影响类型区域：

1)最小隔离区，即将故障隔离开来的最小区域.最小隔离区的后向边界开关唯一，而其前向边界开关可多个；

2)后向区域，即电源与后向边界开关之间的区域；

3)前向区域，即前向边界开关与馈线末端节点构成的区域.

图形库JGraphT中集成的Traverse类提供了广度优先、深度优先和最近优先3种遍历模式.文中应用广度优先搜索技术确定边界开关，形成最小隔离区.当节点故障后，依次遍历搜索其相邻节点，当首次遇到分段开关、断路器或达到末端节点时，终止该方向的搜索.首次遇到的开关为最小隔离区的边界开关，边界开关包围的区域即是最小隔离区.对于后向区域的负荷节点进行故障隔离和恢复供电操作，对于前向区域的负荷节点，在恢复供电之前需要进行转供电判断.

综上所述，基于JGraphT进行配电网数据建模，能够将馈线拓扑结构和元件数据进行整合，具有良好的数据维护性.能够快速检测配网的连通性、区分不同的故障影响区域类型.此外利用其拓扑结构和图论算法开发出符合电力实际需求的程序，例如下文将详细介绍基于JGraphT配电网数据建模的前推回代潮流算法.

2 潮流计算功能开发

面向支路的前推回代法是一种结合配电网特点的潮流算法，具有编程简单、数值稳定性好、计算效率高等优点[11].但前推回代算法仍存在以下两个问题：

1)前推回代计算前需对网络进行繁琐的节点编号，确定各支路功率和节点电压的计算路径和计算顺序；

2)前推回代的研究大多采用邻接表或矩阵表示配电网的拓扑连接关系，未能显示地表现和利用其拓扑结构.一方面随着网络规模的迅速增长，计算量剧增，算法效率低；另一方面重用性较差，当网络结构或者网络参数发生变化时，需重新计算更新参数，严重影响算法性能.

针对以上两个问题，在1.2节配电网数据建模的基础上开发出基于图论的前推回代潮流算法，以图形拓扑直接作为算法的基础，不需要形成相关表或矩阵；该算法为基于图论的递归运算，计算过程与节点编号无关，不需要制定任何编号规则.递归过程优先对节点度数为1的节点进行前推或回代，遇到节点度数大于1时该节点的计算转为等待状态，当该节点上游或下游支路的计算完毕时才对该节点进行计算，以回代过程为例，如图2所示，虚线部分代表该节点已计算.

图2 回代计算过程

算法具体流程如下：

1)程序读取配电网网络参数表，包括节点名称、节点的负荷功率、节点处已有的无功功率补偿值、线路的名称、线路阻抗、线路两端的等效并联电容值等；

2)实例化节点对象与线路对象，基于JGraphT图形库创建出包含配电网络拓扑结构和元件属性值的馈线网络对象(简称feederTopo)，设定潮流算控制参数，即收敛精度以及最大迭代次数；

3)处理配电网馈线对象feederTopo，利用最短路径算法Dijkstra得到各个负荷节点到平衡节点的距离值，并对配电网中各个节点迭代属性赋初值；

4)采用递归的方法，首先回代计算各个节点的注入功率，然后前推计算各个节点的电压值，其中以各个节点到平衡节点的距离值作为控制变量，保证递归时前推回代计算的方向正确.

5)如果收敛条件值小于迭代精度，则输出结果，否则迭代次数k=k+1，转步骤4)继续计算.

基于JGraphT配电网建模开发出的前推回代潮流算法，不需要形成相关表、矩阵和制定编号规则，提高了潮流算法的计算效率.对于大规模配电网故障分析的优势尤为明显.

3 改进模糊遗传算法

3.1 目标函数的数学描述

配电网故障时前向区域带有联络线的负荷需要提供相应的转供方案以恢复供电，转供目标函数即遗传算法的适应度函数.负荷转供通常是一个多目标多约束的优化问题，约束条件主要包括运行约束、供电质量约束和网络拓扑约束3个部分.

1)运行约束即系统潮流约束，如式(1)所示，式中k为控制变量，即支路开关状态，X为状态变量，即P、Q、V等运行参数；

2)供电质量约束包括电压约束、线路容量约束等，如式(2)所示，例如取电压约束时，fmin和fmax分别为电压允许的最小值和最大值，k与X含义与式(1)中相同；

3)网络拓扑约束即配电网保持单电源供电且呈辐射状.网络拓扑约束传统的处理方法需进行相应的遍历，当网络规模较大时会影响程序的运行效率，由于JGraphT集成了JohnsonSimpleCycles、 PatonCycleBase等高效的图算法，因此文中方法能够快速地实现快速的网络拓扑约束判断.

f1(k,X)=0

(1)

fmin≤f2(k,X)≤fmax

(2)

初始目标函数如式(3)所示，

(3)

文中采用序关系分析法[12]确定各项指标的权重，该方法能够充分反映专家意愿，根据待解决问题灵活采用不同的序关系来对指标进行赋权，具有较强的适应性和实用性.序关系分析法的计算过程主要分为以下两个部分：

(4)

其次确定各项指标的序关系和相邻指标的相对重要程度.不同的负荷密度和运行方式下，转供决策的侧重点可能有所不同，因此要求各项指标的权重能随决策问题的改变而灵活变化.序关系分析法指标顺序可调的灵活性可以适应各类决策问题，过程如下：

1)确定转供方案评价准则的指标序关系为x1>x2>…>xn.

2)确定相邻指标之间的相对重要程度.设专家关于指标xk-1与xk的重要程度之比αk-1/αk的理性判断分别为

(5)

3)进行权重系数αk的计算，并根据式(5)得到其他指标的权重，即

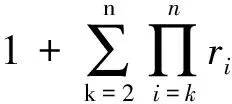
(6)

3.2 遗传算法

遗传算法是通过模拟生物进化程中产生繁殖、变异、竞争和选择的现象来获取全局最优解的优化算法.遗传算法必须结合电网特点才能计算高效，文献[13]中通过节点深度编码技术以保证寻优过程中电网的拓扑约束，但该算法依靠启发规则来确定支路切除点，算法寻优性能没有得到实质性地提升.文中将从初始集合、变异算子和交叉算子3个方面进行改进.

1)遗传算法属于随机优化算法，其收敛于最优解的速度与其初始解密切相关，当初始解与最优解相似时，可以提高收敛速度.文中采用遗传算法的二进制编码，直接用0和1表示开关闭合状态，以避免开关按个数编号造成染色体长度过长，同时省去二进制与十进制的转换过程.实际运行过程中，当待转供区域联络开关个数为N，分段开关个数为M时，则待转供区域闭合开关占总开关数的比例为M/(M+N)，负荷转供后该区域的开关闭合率应保持接近该比例以保证电网的辐射性，因此初始化的二进制编码中数值为“1”的位数占染色体总长的比例，即线路开关闭合率，应该取M/(M+N)；

2)在传统的遗传算法中，交叉算子Pc和变异算子Pm取为固定值，当用于多变量优化问题时效率不高，影响算法的性能，而且种群个体容易发生早熟[14].为了避免早熟收敛，同时提高计算速度，文中算法的变异算子和交叉算子将根据程序运行结果进行动态调整，具体应满足以下3个原则：

1)交叉算子、变异算子在进化前期应取较大值以促进收敛，中期取中等值以充分进行局部搜索，后期取较小值以保护最优解；

2)进化前期当适应度函数值的离散程度变化较小时可能出现早熟，应适当减少变异算子、增大交叉算子，进化后期为避免对算法稳定性造成冲击以及保护最优解，通常交叉算子、变异算子均取较小值；

3)进化前期当平均适应度与最佳适应度函数值非常接近时可能出现早熟，应适当减少交叉算子、增大变异算子，进化后期通常交叉算子、变异算子均取较小值.

从以上原则不难看出，交叉算子、变异算子的调整与算法的进化代数有着密切关系，遗传代数的功能相当于模拟退火法的温度，往往是容易被忽略的重要参数.

文中基于开源遗传算法库Jenetics[15]编写馈线转供电优化算法.Jenetics是基于Java开发的用来解决遗传问题的算法库，它提供了对应遗传算法的各种相关类，如染色体类Chromosome、基因类Gene、表现型类Phenotype和适应度函数类Function等，能够实现面向对象编程，扩展性良好.

3.3 模糊逻辑控制器

遗传算法运行过程交叉率Pc和变异率Pm的调整是一个复杂的问题，涉及因素较多，难以全面、精确地描述.文中采用模糊理论来处理该问题，根据3.2节中提出的变异算子和交叉算子动态调整的3个原则，文中定义的模糊逻辑控制器FLC含有两个输出变量(变异算子Pm、交叉算子Pc)和3个输入变量，输入变量包括遗传代数(称n)、适应度函数值方差的变化量(称E1)以及平均适应度与最佳适应度函数值差值(称E2).

n=i/N, 0≤i≤N

(7)

(8)

(9)

(10)

模糊规则如表1所示，共27条规则，k为相应的规则序号.对于输入量n，s代表进化初期，m代表进化中期，l代表进化末期；对于输入量E1、E2和输出量Pc、Pm，s代表小概率，m代表中概率，l代表大概率.

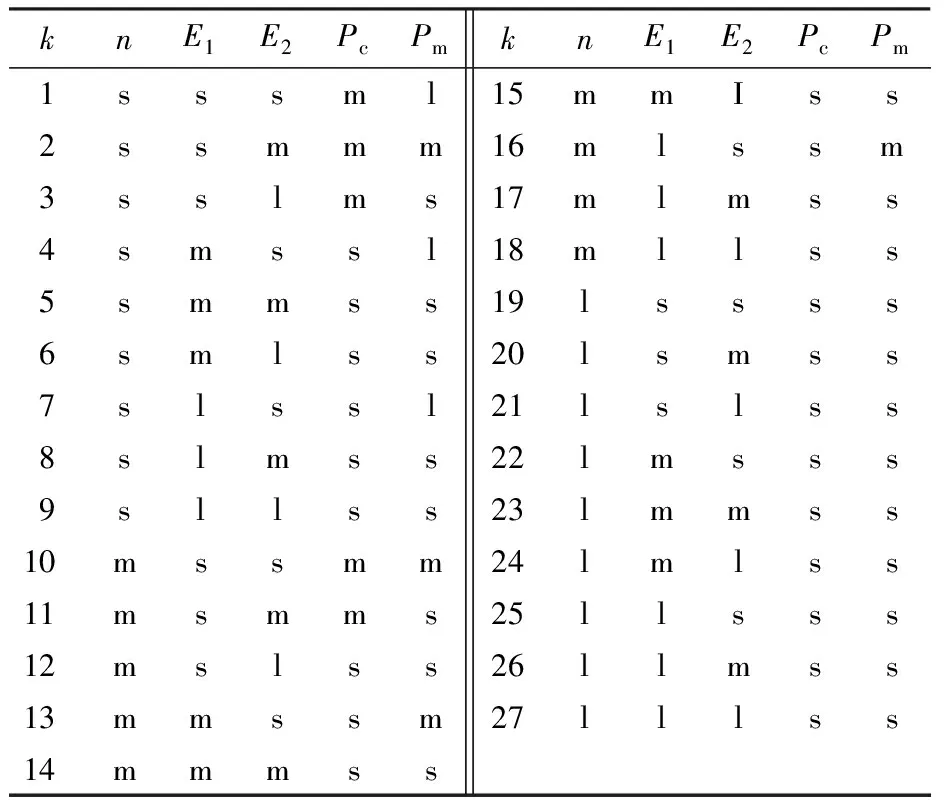
表1 模糊逻辑控制表

文中采用开源模糊逻辑控制库jFuzzyLogic[16]构建模糊逻辑控制器，jFuzzyLogic支持用户通过编写模糊逻辑控制语言(FCL)来实现特定的模糊逻辑控制功能.以输入量n和规则1为例.

n的模糊化过程用FCL语言表示为

FUZZIFY n

TERM s:=(0,1)(0.25,1)(0.5,0);

TERM m:=(0.25,0)(0.5,1)(0.75,0);

TERM l:=(0.5,0)(0.75,1)(1,1);

END_FUZZIFY

规则1用FCL语言表示为

RULE 1:IF A1IS s AND A2IS s AND A3IS s THENPcIS l.

图3为文中基于图论和改进模糊遗传算法进行配电网转供的程序流程图.

图3 负荷转供流程图Fig.3 Flow chart of load transfer

4 算例

以美国PG&E69节点配电网作为研究对象对文中方法进行检验.如图4所示，PG&E69节点配电网系统基准电压为12.66 kV，包含69个节点，74条支路，其中5条为联络开关支路，图中用虚线表示.节点负荷、支路阻抗等参数详见文献[17].潮流收敛精度为0.000 01，根据文中基于JGraphT配电网建模开发出的前推回代潮流算法，迭代到第3次时即达到精度值，而文献[18]和文献[19]分别在第4次和第6次才能达到精度要求，文中潮流算法以图形拓扑直接作为算法的基础，提高了潮流计算程序的运行效率.

图4 PG&E69节点配电网

根据序关系分析法确定的目标函数，分别采用遗传算法GA[6]、模糊遗传算法FGA[8]和文中的改进模糊遗传算法IFGA(Improved Fuzzy Genetic Algorithm)对该网络进行故障转供.算法种群数量为150，进化代数为100，初始交叉率Pc为0.5，初始变异率Pm为0.1，采用GA进行故障转供时，保持Pc、Pm不变，采用FGA和IFGA时，对Pc、Pm使用不同模糊规则进行实时控制.3种算法分别计算50次取平均值，表2所示为3种算法的具体计算结果.

由表2可知，在同样的种群规模、同样的约束条件下，3种算法均能够最大程度地减少故障停电负荷节点，但IFGA算法在开关动作次数上和网络优化降低网损值上占优.3种算法的收敛过程如图5所示.由图可见，IFGA算法的收敛速度优于算法FGA和GA，IFGA和FGA算法分别在迭代次数为32和48时接近最优值，而GA算法在迭代次数为57时才接近最优值.可见IFGA和FGA相比，更大程度地改善了GA的性能，提高了成熟收敛速度.

表2 计算结果比较1)

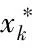
图5 3种算法寻优过程比较

5 结语

文中基于图形库JGraphT进行配电网数据建模，将馈线拓扑结构和元件参数整合在一起，显式地利用配电网拓扑结构；基于图论递归运算的前推回代算法不需要进行节点编号规则制定，避免了冗杂的邻接表或矩阵存储模式，程序运行效率提高.结合电网特点提出改进的模糊遗传算法，采用以待转供区域支路开关状态为基础的二进制编码，提出根据实际开关闭合率调整遗传算法的初始解，保持初始解与最优解的相似性；通过对模糊输入量和模糊规则进行完善，制定遗传算子的修正方法，改进模糊遗传算法IFGA能够对遗传算子进行更合理的控制，提高收敛速度，避免不成熟收敛的发生.算例结果表明文中算法在潮流计算效率和寻优效率均具有更好的效果.

满足供电恢复的实时性和有效性是配电网故障恢复的基本要求，因此进一步提高供电恢复速度和优化性能仍是未来研究的重点.

[1] 王辉,黄丽华,陈俊红,等.辐射型配电网络可靠性中节点编号优化算法的研究 [J].电力系统保护与控制,2010,38(5):5- 9,15. Wang Hui,Huang Li-hua,Chen Jun-hong,et al.A study of reliability assessment node number optimization algorithm for radial distribution system [J].Power System Protection and Control,2010,38(5):5- 9,15.

[2] 张剑,袁晓冬.基于深度搜索的配电网前推回代潮流计算方法 [J].电气应用,2015(2):16- 19. Zhang Jian,Yuan Xiao-dong.Power flow calculation me-thod based on the depth of the search distribution network [J].Electro technical Application,2015(2):16- 19.

[3] 刘莉,赵璇,姜新丽,等.基于层次矩阵的配电网拓扑分析与潮流计算 [J].电力系统保护与控制,2012,40(18):91- 94. Liu Li,Zhao Xuan,Jiang Xin-li,et al.Distribution network topology analysis and flow calculation based on layer matrix [J].Power System Protection and Control,2012,40(18):91- 94.

[4] 徐青山,刘中泽,杨永标,等.改进的配电网三相潮流计算方法 [J].电力系统及其自动化学报,2014(9):23- 29. Xu Qing-shan,Liu Zhong-ze,Yang Yong-biao,et al.Improved method of distribution network three-phase power flow calculation [J].Proceedings of the CSU-EPSA,2014(9):23- 29.

[5] Sheng Si-qing,Ma Zhi-gang,Wu Jing．Distribution network fault restoration based on improved adaptive genetic algorithm [C]∥Proceedings of Intelligent Computation Technology and Automation Conference．Zhangjiajie：[s.n.],2009:78l- 786.

[6] Prasad P V,Sivanagaraju S,Sreenivasulu N.Network reconfiguration for load balancing in radial distribution systems using genetic algorithm [J].Electric Power Components and Systems,2008,36(1):63- 72.

[7] Yogendra Kumar,Biswarup Das,Jaydev Sharma,et al.Multiconstraint service restoration of electric power distribution system with priority customers [J].IEEE Trans On Power Delivery,2008,23(1):261- 270.

[8] 李德华,王韶,刘洋,等.模糊遗传算法和蚁群算法相结合的配电网络重构 [J].电力系统保护与控制,2009,37(17):26- 31. Li De-hua,Wang Shao,Liu Yang,et al.Distribution network reconfiguration based on the combination of fuzzy genetic algorithm and ant colony algorithm [J].Power System Protection and Control,2009,37(17):26- 31.

[9] Prasad K,Sahoo N C,Ranjan R,et al.A new computational approach for optimal reconfiguration of radial distribution systems using a fuzzy controlled genetic algorithm [J].The International Journal for Computation and Mathematics in Electrical and Electronic Engineering,2006,25(4):862- 882.

[10] Naveh B,Contributors.JGraphT [EB/OL].[2015- 01- 20].http:∥www.JGraphT.org.

[11] Fan Ji-Yuan,Zhang Lan,McDonald J D.Distribution network reconfiguration:single loop optimization [J].IEEE Transactions on Power Systems,1996,11(3):1643- 1647.

[12] 欧阳森,杨家豪,耿红杰,等.面向台区管理的台区状态综合评价方法及其应用 [J].电力系统自动化,2015,39(11):187- 192. Ou Yang-sen,Yang Jia-hao,Geng Hong-jie,et al.Comprehensive evaluation method of transformer area state oriented to transformer area management and its application [J].Automation of Electric Power Systems,2015,39(11):187- 192.

[13] 黄弦超，Taylor G Tareth.基于节点深度编码技术的配电网故障恢复 [J].电力系统自动化，2011,35(6):40- 44. Huang Xian-chao,Taylor G Taylor.Service restoration of distribution networks based on node-depth encoding technique [J].Automation of Electric Power System,2011,35(6):40- 44.

[14] Deb Kalyanmoy,Prata Amrit,Agarwal Sameer,et al.A fast and elitist multi-objective genetic algorithm:NSGA [J]IEEE Transactions on Evolutionary Computation,2002,6(2):182- 197.

[15] Wilhelmstötter Franz.Jenetics [EB/OL].[2015- 01- 20]http:∥www.jenetics.io/.

[16] Cingolani P.jFuzzyLogic [EB/OL].[2015- 01- 20].http:∥jfuzzylogic.sourceforge.net/html/index.html.

[17] Savier J S，Das D．Impact of network reconfiguration on loss allocation of radial distribution systems [J]．IEEE Trans on Power Delivery，2007，22(4)：2473- 2480.

[18] 李如琦,谢林峰,王宗耀,等.基于节点分层的配网潮流前推回代方法 [J].电力系统保护与控制,2010,38(14):63- 66. Li Ru-qi,Xie Lin-feng,Wang Zong-yao,et al.Back/ forward substitution method for radial distribution load flow based on node-layer [J].Power System Protection and Control,2010,38(14):63- 66.

[19] 王峥，丛培杰.基于改进前推回代法的辐射状配电网潮流计算 [J].东北电力技术，2008(2):9- 12. Wang Zheng,Cong Pei-jie.Power flow calculation for radial distribution network based on forward/backward substitution method [J].Northeast Electric Power Technology,2008(2):9- 12.

A Load Transfer Method for Power Distribution Networks Based on Graph Theory and Improved Fuzzy Genetic Algorithm

WuZhi-gangMaYi-song

(School of Electric Power, South China University of Technology, Guangzhou 510640, Guangdong, China)

In view of the fault recovery of complicated power distribution networks, a load transfer method for power distribution networks is proposed based on the graph theory and the improved fuzzy genetic algorithm. First, the topological structure and component parameters of feeders are integrated together by means of the JGraphT-based data modeling of power distribution networks, and by taking advantage of the topological structure of power distribution networks explicitly, the tedious node encoding rules and the storage modes in the form of miscellaneous adjacency lists or matrices are avoided. Next, with the help of the graph theory algorithms integrated in JGraphT, different types of fault sections are quickly distinguished and the topological constraint is rapidly determined. Then, a forward-backward sweep method based on the recursive graph theory is developed. Finally, an improved fuzzy genetic algorithm is proposed according to the characteristics of power distribution networks. In the proposed algorithm, the initial solutions and genetic operators of the genetic algorithm are dynamically adjusted so as to improve the optimizing performance of the proposed algorithm, and the fuzzy inputs and fuzzy rules are revised reasonably to improve the convergence rate of the genetic algorithm and avoid the premature convergence. Simulation results show that the proposed algorithm is superior to the other methods in terms of power flow calculation and optimization efficiency.

JGraphT; load transfer;electric lood flow;genetic algorithm

2015- 03- 26

国家高技术研究发展计划项目(2012AA050209)；华南理工大学中央高校基本科研业务费面上项目(x2dlD2141600) Foundation item: Supported by the National High-Tech R&D Program of China(2012AA050209)

武志刚(1975-)，男，博士，副教授，主要从事电力系统仿真、复杂网络理论研究.E-mail： epzgwu@scut.edu.cn

1000- 565X(2015)12- 0048- 07

TM 715

10.3969/j.issn.1000- 565X.2015.12.007