陀螺寻北仪的精度评定方法
蒋庆仙,段渭超
1. 西安测绘研究所,陕西 西安,710054;2. 地理信息工程国家重点实验室,陕西 西安,710054
陀螺寻北仪的精度评定方法
蒋庆仙1,2,段渭超1,2
1. 西安测绘研究所,陕西 西安,710054;2. 地理信息工程国家重点实验室,陕西 西安,710054
寻北精度是陀螺寻北仪的主要技术指标之一,反映了寻北观测值相对其真值的离散度。当观测值遭受系统误差或粗差污染时,采用建立在观测值服从正态分布基础上的最小二乘精度模型,参数估值及精度评定会受到严重影响。为了完善陀螺寻北仪的精度评定方法,本文厘清了陀螺寻北仪的精度内涵,研究了顾及粗差影响的精度模型,提出了结合中位数估计与抗差估计各自优势的数据处理算法,使参数估计和精度评定更可靠、更有参考价值,可以作为考核、评定该类装备的重要依据。
陀螺寻北仪;精度评定;粗差;抗差估计
1 引 言
陀螺寻北仪是一种采用陀螺仪作为角速率传感器、利用陀螺原理通过测量地球自转角速率测定真北方位的仪器。其主要特点是:寻北精度高、测量时间短、不受气候条件限制,在任何时间和地点(高纬度地区除外)都可以自主寻北测量[1-3]。随着惯性技术、电子技术和计算机等技术的进步,陀螺寻北仪在军事和民用领域中均得到了日渐广泛的应用[4,5]。
在各种教科书和测绘技术资料中,采用“精度”描述测绘仪器的主要性能。所谓精度是指测量误差分布的密集或离散的程度,即离散度的大小。仪器测量精度高指的是该仪器的测量误差小,观测值的重复性好,观测结果也更接近测量值的真值。这里所指真值是各测量值的数学期望,即理论平均值。在实际测量中由于无法获得测量值的真值,在检定仪器精度时,通常采用更高精度仪器获得的观测结果代替真值。按照国际标准ISO17123规定的测绘仪器精度检定方法,用“accuracy”表示测量结果与被测量“真值”之间的一致程度,它是随机误差和系统误差的表述[6]。
寻北精度(有的文献也称准确度、精确度)是陀螺寻北仪的主要技术指标之一。影响寻北精度的因素有很多,外界环境的任何微弱干扰都会反映到陀螺寻北仪上,造成测定的方位角有偏差。寻北精度反映了陀螺寻北仪的测量值相对其“真值”的离散度,是指陀螺寻北仪给出的观测结果接近于“真值”的能力[7,8]。若将仪器架设在已知真北方位的基准边上,则多次试验测出的方位角与实际方位角进行对比,求出的标准差即为陀螺寻北仪的精度。这是建立在观测值服从正态分布基础上的最小二乘精度模型。当观测值遭受系统误差或粗差污染时,参数估值及其精度评定会受到严重干扰,在数据处理中必须减弱或消除系统误差和粗差的影响。在消除了系统误差的前提下,采用结合中位数估计与抗差估计优势的参数估计方法,对陀螺寻北仪进行精度评定,获得的结果能够反映寻北仪的真实精度,是一种可以在同类装备中推广使用的精度评定方法,对考核和评定该类装备有重要意义[9,10]。
2 陀螺寻北仪精度与地理纬度的关系
任何一种原理的惯性级陀螺都可以敏感地球自转角速率,而每一种陀螺又可以采用多种方法完成寻北测量。目前陀螺寻北法主要有罗经法、角度法和速度法[5]。不管采用何种方法,陀螺寻北仪都是依靠陀螺敏感地球自转角速率的水平分量ωH=ωεcosφ进行寻北测量,而地球自转角速率的垂直分量ωV=ωεsinφ是有害分量(ωε为地球自转角速率,φ为测站的地理纬度)。在仪器设计和使用中,总是设法将陀螺输入轴呈水平放置,以便于消除地球自转角速率垂直分量的影响。在赤道上,水平分量达到最大值,而垂直分量为零,陀螺寻北仪具有最好的寻北能力。在两极,水平分量为零,而垂直分量达到最大值,陀螺寻北仪失去寻北作用。在高纬度地区,陀螺寻北仪的精度很低。可见,陀螺寻北仪的精度是地理纬度的函数,且随着地理纬度的增加而降低。在评定陀螺寻北仪精度时,必须给出测站的地理纬度,否则是没有意义的。因而《陀螺寻北仪通用规范》将陀螺寻北仪的精度定义为σ/cosφ(σ为一次寻北测量的标准偏差)[11]。这样,在任意纬度条件下,陀螺寻北仪的精度可写为[12]
σφ=σ0/cosφ
(1)
式中,σ0定义为赤道精度,即陀螺寻北仪在赤道处的寻北精度,是陀螺寻北仪的固有精度。
国外研究机构曾利用GYROMAT2000陀螺经纬仪进行过纬度试验,验证了仪器的精度随着地理纬度的增加而降低,其结果表明符合式(1)的关系。
目前国外有三种表示陀螺寻北仪精度的方法:(1)给出仪器工作的纬度范围及在最高纬度下的精度;(2)用赤道精度表示,如式(1)所示;(3)分成两项表示,与纬度无关的精度和与纬度有关的精度。
由于陀螺寻北仪的仪器常数变化对任一次测量的精度都会造成影响,国外军用标准中常采用“总误差”表示寻北精度。
(2)
式中,n为观测次数,C为仪器常数。
3 陀螺寻北仪的精度模型
在陀螺寻北仪的测量过程中,由于各种环境因素的影响,观测数据不可避免受到多种噪声的污染,即观测值中可能同时含有随机误差、系统误差和粗差,其中系统误差和粗差是影响陀螺寻北仪测量结果和质量评定可靠性的主要因素。在评定陀螺寻北仪精度前,通常先要设法消除系统误差的影响,使其对测量结果的影响可以忽略不计。目前常用的系统误差处理方法是先使用统计方法检验是否存在系统误差,如存在则进行误差补偿或将系统误差转换为随机误差[13]。
3.1 仅考虑随机误差的精度模型

设在静基座条件下获得一组陀螺寻北仪测量值{xi}(i=1,2,…,n),误差方程为
(3)

设观测值独立,pi为第i个观测值的权。参数的最小二乘解为
(4)
相应的内符合精度模型和外符合精度模型分别为
(5)
(6)
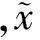
内符合精度反映的是观测值相对估值的离散程度,外符合精度则反映了参数估值相对其“真值”的偏离程度,因而获得精度的可靠性更高。在实际评定测量成果的精度时,一般无法事先给出未知参数的真值,在采取一定措施减弱系统误差和粗差的影响后,可以使内符合精度模型尽可能表征未知参数估值的真实精度,因此,常使用内符合精度模型。
3.2 顾及粗差的精度模型
3.2.1 基于粗差剔除的精度模型
粗差剔除是指通过检验发现含有粗差的观测值,并将其从观测值中剔除,再用余下的观测值求解未知参数估值并进行精度评定,使用该方法要求有较多的观测值。
设观测值中有m个粗差,剔除粗差后,由最小二乘准则得
(7)
内符合精度模型为
(8)
3.2.2 基于抗差估计的精度模型
抗差估计是在粗差不可避免的情况下,通过选择适当的估计方法使未知参数估值尽可能避免粗差的影响,得出正常模式下的最佳估值。实际应用时,常使用权因子降低异常观测值的权,从而降低该观测值对未知参数估值的影响[9,10]。
未知参数的抗差估值为
(9)
内符合精度模型为
(10)

3.3 几种精度模型的分析与比较
测量不可避免地存在观测误差,且观测误差会随着观测条件的变化而变化。在数据处理时,误差不同,所选用的误差处理方法也会不同。即使是相同的误差,其处理方法也不一定相同。两种处理粗差的精度模型的差别在于:①观测值的维数不同,粗差剔除法的观测值个数要少于抗差估计;②权不同,(8)式中的权为剔除粗差后余下观测值的权,(10)式中的权为抗差估计迭代结束时观测值的等价权;③残差不同,(8)式中的残差为剔除粗差后剩余观测值的残差,(10)式中的残差是经过粗差处理后的观测残差。因此,在处理含有粗差的测量数据时,必须依据实际的粗差处理方法选择对应的精度模型,以确保能真实表征测量成果的精度和可靠性。
4 陀螺寻北仪的精度评定
由于陀螺寻北仪观测值中存在系统误差和粗差,采用最小二乘估计得到的结果无法准确表征陀螺寻北仪的精度和可靠性。结合中位数估计与抗差估计各自的优势,采用中位数估计求解每个测回的估值,可以保证即使有50%的数据受到粗差的污染,也能够得到可靠的估值;采用抗差估计求解最终的估值,既减少了计算量,又可以获得可靠的估计效果,是一种有效、可靠的参数估计方法[9,10,14]。
实验地点的地理纬度为34°13.92′。光纤陀螺的零偏稳定性为0.02°/h,采样频率为400Hz。常温条件下(25°C)在实验室进行了光纤陀螺寻北仪的测试及精度评定,进行了8组寻北试验,每个测量位置的采样时间为70s。对陀螺信号进行了频谱分析,低通滤波后噪声的功率谱密度如图1所示。由此可知,低通滤波去除了高频噪声,周期噪声的频率主要集中在10~20Hz之内,幅度为1dB/Hz。
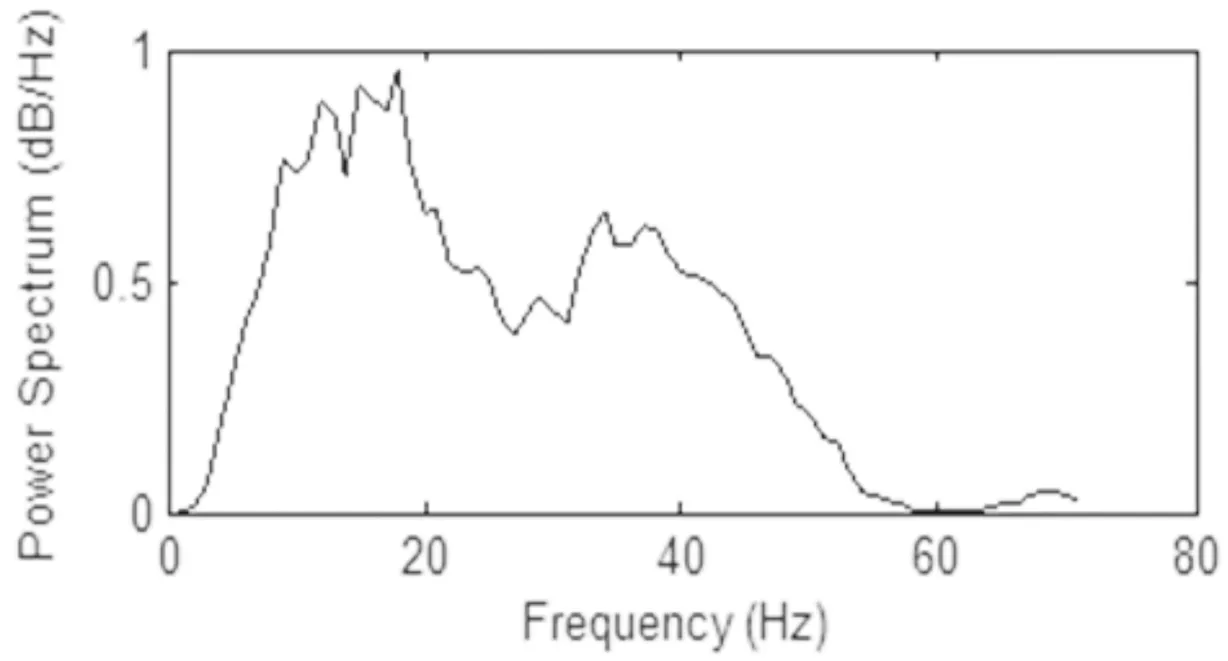
图1 低通滤波后噪声的功率谱密度
在采用二等天文测量方法获得基准边真北方位的基础上,结合经纬仪的观测结果计算得到待测方位角为153°04′56″。在解算中采用观测值的均方根误差(RMS)评定寻北精度, 对实验数据采
用如下4个方案解算。
(1)(LS)最小二乘估计;
(2)(LS+RO)每一组观测值取均值作为抗差初值,抗差估计;
(3)(RO+RO)每一组观测值取中位数作为抗差初值,抗差估计;
(4)(MEDIAN)中位数估计。
限于篇幅仅给出各个方案的最后计算结果,见表1。在求解得到8个测回的估值后,方案2将8个估值取均值作为抗差初值求解最终的估值;方案3将8个估值取中位数作为抗差初值求解最终的估值;方案4分别采用抗差估计、最小二乘估计和中位数估计求解最终的估值。表2给出每一测回方位角估值的权值,权反映了每个测回的估值对本方案中方位角估值的贡献。在最小二乘估计中每一测回估值平等参与方位角最终估值的解算,权全部取1。在抗差估计中使用权因子降低异常观测值的权,由算法自动确定每一测回估值的等价权。
表1 观测数据处理结果(纬度:34°13.92′,单位:°)
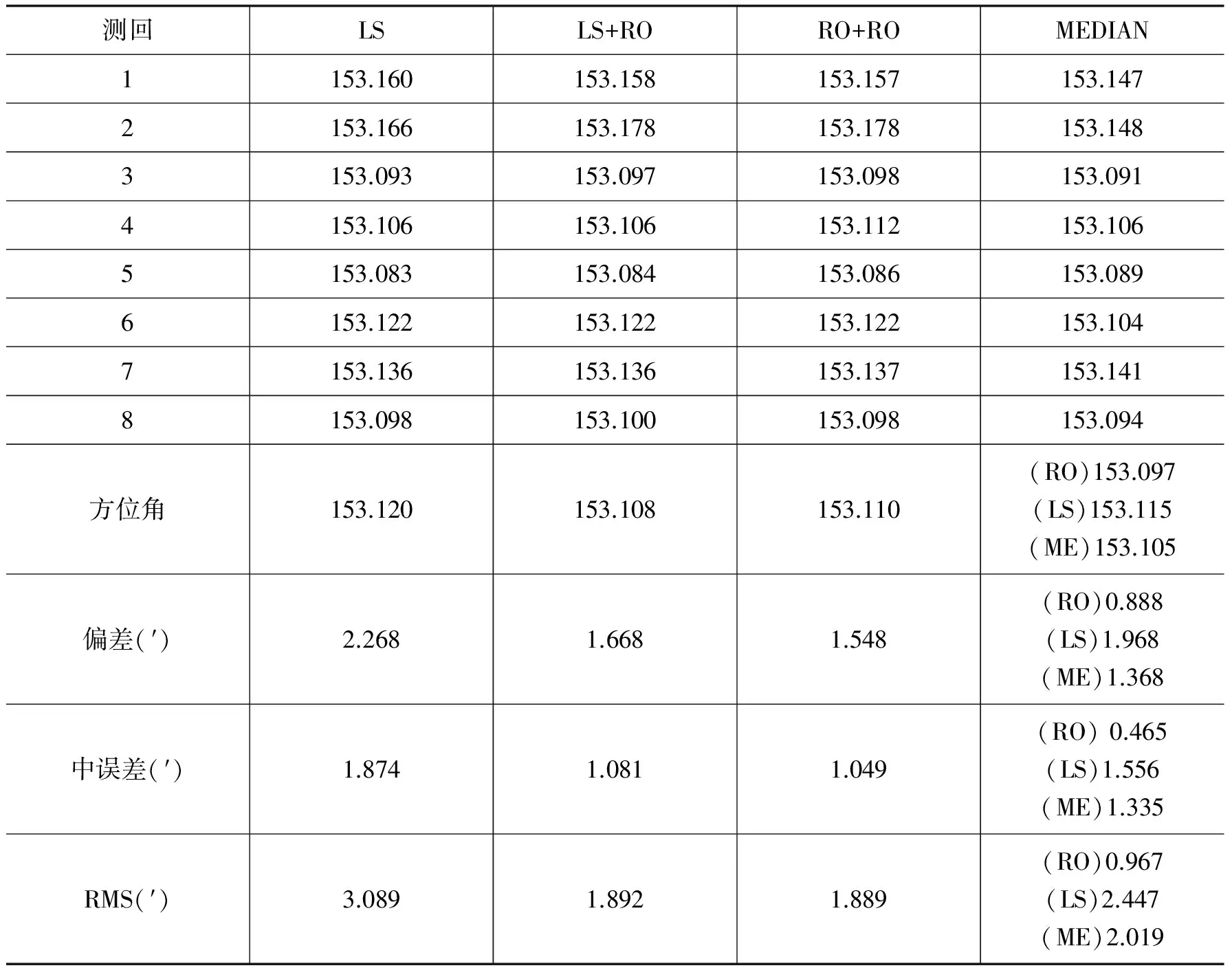
测回LSLS+RORO+ROMEDIAN1153.160153.158153.157153.1472153.166153.178153.178153.1483153.093153.097153.098153.0914153.106153.106153.112153.1065153.083153.084153.086153.0896153.122153.122153.122153.1047153.136153.136153.137153.1418153.098153.100153.098153.094方位角153.120153.108153.110(RO)153.097(LS)153.115(ME)153.105偏差(′)2.2681.6681.548(RO)0.888(LS)1.968(ME)1.368中误差(′)1.8741.0811.049(RO)0.465(LS)1.556(ME)1.335RMS(′)3.0891.8921.889(RO)0.967(LS)2.447(ME)2.019
表2 每一测回方位角估值的权值
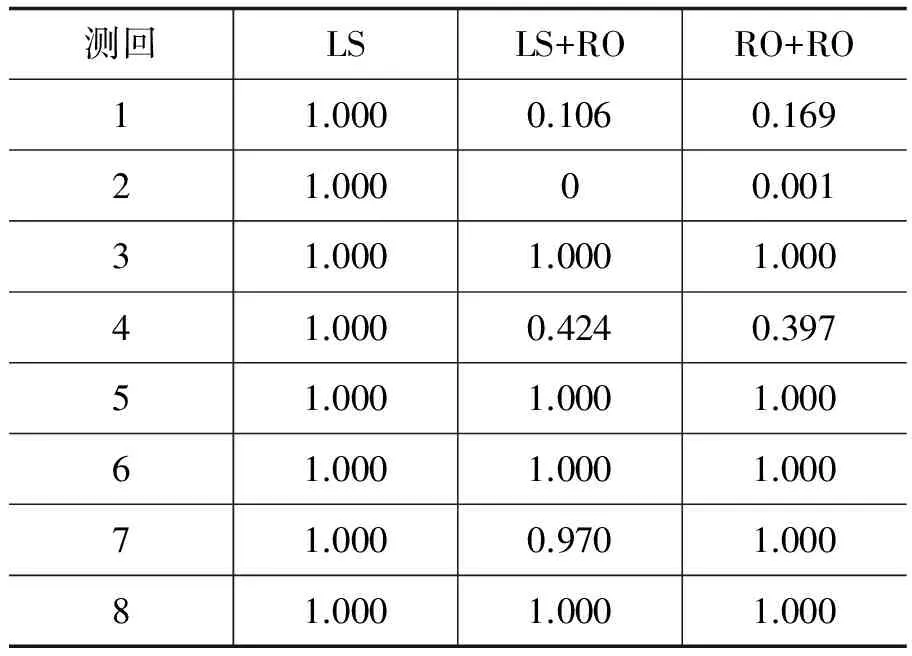
测回LSLS+RORO+RO11.0000.1060.16921.00000.00131.0001.0001.00041.0000.4240.39751.0001.0001.00061.0001.0001.00071.0000.9701.00081.0001.0001.000
由表1的计算结果可知,采用中位数估计和抗差估计组合的参数估计方法获得的方位角与待测方位角参考值的偏差仅为0.888°,寻北精度(RMS)为0.967′,优于其他方法的结果。简单分析:(1)最小二乘估计不具有抗差性,其控制粗差影响的能力要低于抗差估计。由于最小二乘估计过分地迁就粗差测值,而使估值受到了歪曲,因而获得的精度评定结果最差。(2)由于抗差估计通过等价权对异常观测值进行控制,消除或减弱了异常观测值的影响,保证了观测信息的利用率与估计结果的可靠性,从而获得较高的估计精度。(3)在观测数据中存在异常观测值的情况下,采用结合中位数估计与抗差估计各自优势的数据处理算法,既减少了计算量,又获得了可靠的估计效果,使参数估计和精度评定更可靠、更有参考价值。
5 结束语
寻北精度是陀螺寻北仪的主要技术指标之一,当观测值遭受系统误差或粗差污染时,采用建立在观测值服从正态分布基础上的最小二乘精度模型,参数估值及其精度评定会受到严重干扰。抗差估计能够有效减弱异常干扰对参数估计的影响,并且可以将异常干扰剔除而不影响其余有用信号,能够最大限度地削弱了粗差对陀螺方位角估值的影响,获得较高的寻北精度。在消除陀螺寻北仪测量值中系统误差的前提下,提出了结合中位数估计与抗差估计优势的参数估计方法。试验证明:采用抗差估计处理陀螺寻北仪的观测成果,获得的结果能够反映寻北仪的真实精度,是一种可以在同类装备中推广使用的精度评定方法。该方法可用于指导制定陀螺寻北仪的检定规程,为完善陀螺寻北仪的精度评定、研究陀螺寻北仪的效能评估和验证提供重要技术支撑。
[1]梁阁亭,惠俊军,李玉平.陀螺仪的发展及应用[J].飞航导弹,2006(4):38-40.
[2]李敏,王志乾,黄波.基于动调陀螺的多位置捷联寻北仪研制[J].仪表技术与传感器,2010(5):19-21,46.
[3]夏桂锁,于润桥,程强强等.基于惯性/地磁组合技术的全自动陀螺经纬仪的研制[J].传感技术学报,2013,26(7):966-970.
[4]AndrewWethereltandPaulHunt.UndergroundAzimuthDeterminationsUsingaWildGAK1 [C]//.FIGXXIIInternationalCongress,Washington,D.C.USA,2002:1-5.
[5]许卓兵.基于DSP的全姿态挠性陀螺寻北仪的研制[D].上海:上海交通大学,2002.
[6]杨俊志,张贵和.测绘仪器准确度的表示与检定[J].测绘科学,2006,31(3):69-70.
[7]蒋庆仙.陀螺经纬仪检定方法探讨[J].测绘科学与工程,2008,28(3):54-58.
[8]蒋庆仙,马小辉,陈晓璧.陀螺经纬仪的仪器常数及其测定[J].测绘科学,2008,2:152-154.
[9]蒋庆仙,王成宾,马小辉.利用中位数进行光纤陀螺信号抗差估计[J].武汉大学学报·信息科学版,2011,36(6):656-659.
[10]蒋庆仙,马小辉,陈晓璧等.两种抗差估计在陀螺信号处理中的比较[J].测绘科学,2011,36(5):49-51.
[11]国防科学技术工业委员会.陀螺寻北仪通用规范[S].1997.
[12]余祖荫.陀螺寻北仪的精度与评定方法[J].测绘通报,1988(1):22-24.
[13]崔先强,秦峰,唐颖哲.大地测量成果的质量评价模型[J].测绘科学与工程,2005,25(1):11-14.
[14]JIANGQing-xian,BAIYun-chao,MAXiao-hui.FastDynamicNorth-SeekingalgorithmbasedonRobustEstimation[J].传感技术学报,2013,26(1):43-48.
Accuracy Assessment for Gyro North Seeker
Jiang Qingxian1,2,Duan Weichao1,2
1. Xi’an Research Institute of Surveying and Mapping,Xi’an 710054,China 2. State Key Laboratory of Geo-information Engineering,Xi’an 710054,China
North-seeking accuracy is one of the important technical indicators for gyro north seeker, which reflects the dispersion of north seeker observations compared with that of the actual value. When the observations are contaminated by systematic errors and outlying errors, the least squares estimates of accuracy is established based on the observations following the normal distribution, and the parameter estimation and accuracy obtained by the model will be severely disturbed. In order to improve the accuracy assessment for gyro north seeker, this paper distinguishes the accuracy meaning of gyro north seeker, studies the accuracy models considering outlying errors and proposes the data processing algorithm integrated with median estimation and robust estimation. The algorithm makes the parameter estimation and accuracy assessment for the gyro north seeker more reliable and useful, which can be taken as the important basis in checking and assessing this type of equipments.
gyroscope north seeker;accuracy assessment;outlying errors;robust estimation
2015-04-07。
国家自然科学基金资助项目(41374003)。
蒋庆仙(1969—),女,高级工程师,主要从事陀螺定向技术研究。
P207
A

