北斗三频载波最优线性组合分析
常志巧,曹纪东 ,董恩强
1.北京卫星导航中心,北京,100094;2.上海天文台,上海,200030
北斗三频载波最优线性组合分析
常志巧1,2,曹纪东1,董恩强1
1.北京卫星导航中心,北京,100094;2.上海天文台,上海,200030
北斗卫星导航系统具有三个频率的相位观测量,不但在周跳探测和模糊度求解中具有较大优势,在载波相位相对定位中也可以提高定位精度。本文在三个频点的模糊度正确固定的基础上,对于短基线相对定位,假定通过相位观测的双差组合,只剩下相位观测噪声,以观测噪声最小为条件,推导了短基线相对定位的最优线性组合观测量;对于中长基线相对定位,假定通过相位观测的双差组合,电离层延迟影响是主要误差,以消除电离层影响且噪声最小为条件推导了中长基线相对定位的最优线性组合观测量。通过实测和仿真计算表明,最优组合观测量的相对定位精度高于其他组合观测量。
北斗卫星导航系统;相对定位;载波相位观测;最优组合;短基线;中长基线
1 引 言
目前双频组合观测值理论在模糊度求解和周跳探测领域得到广泛应用。为了保持模糊度的整周特性,线性组合系数要求为整数[1]。当模糊度正确求解后,利用新的线性组合观测值以提高相对定位的精度,这时线性组合系数不受整数特性的约束,范围更加广泛。在GPS短基线相对定位中,由于消除了轨道误差、电离层误差和对流层误差,观测噪声成为影响位置精度的主要误差源,这时通常采用噪声最小的窄巷组合来提高定位精度。对于中长基线(>10km),双差后残余的电离层延迟误差仍较大,是影响位置精度的主要误差源,这时通常采用消电离层组合来提高定位精度[2,3]。
北斗卫星导航系统具有三个频率的伪距和相位观测量,当模糊度成功解算后,可以获得更多有益的组合进行相对定位解算。本文以提高相对定位精度为目标,通过理论推导给出针对短基线和中长基线相对定位的最优观测组合。
2 三频组合观测模型
三频载波相位组合观测值的一般形式为[4]:
(1)
式中,i、j、k为组合系数;f1、f2、f3为相应频率。在模糊度求解和周跳探测中,为了保持线性组合观测值模糊度的整数特性,i、j、k一般为整数[5];一旦模糊度被正确固定后,相对定位中的未知参数变为基线向量,这时i、j、k可以为任意实数。
组合观测值观测方程为:
(2)
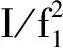
(3)
如果认为原始相位观测的噪声εΦ1、εΦ2、εΦ3是独立的且方差相等,则有:
(4)
(5)
公式(5)中βn被定义为相位噪声因子(以m为单位的比值)。
3 相对定位的最优线性组合
3.1 短基线相对定位
当基线长度较短时(<10km),认为通过双差可以消除电离层和对流层以及轨道误差的影响,这时对相对定位影响最大的因素是载波相位的观测噪声[2],为了简单起见,认为没有其他因素的影响。由于解算出了原始信号上的模糊度,也就是得到了高精度的距离观测值,这时高精度相对定位不要求组合系数为整数,只要满足下式定义即相位噪声因子最小的组合就为最优组合。
(6)
经推导可得满足相位噪声因子最小的组合系数表达式为:
(7)
令i=1,将区域卫星导航系统的三个频率f1=1561.098,f2=1207.14,f3=1268.52MHZ[6]代入公式(7),可得表1中的噪声最小的观测组合(表中第一行)。
表1 几种噪声较小的组合观测量特性
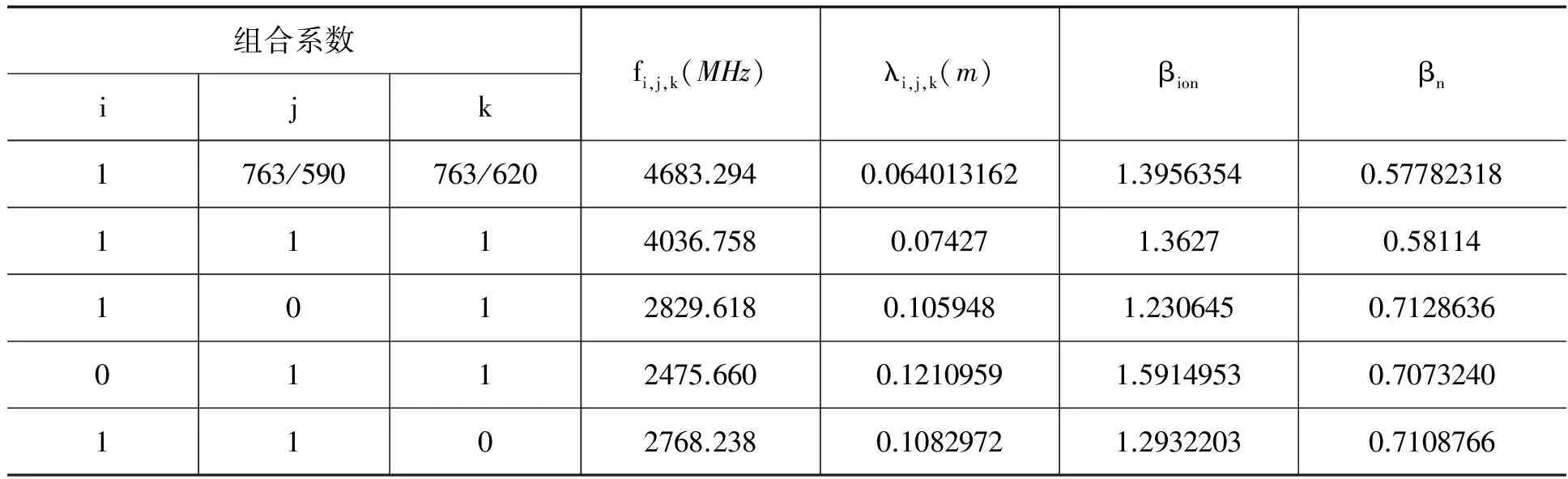
组合系数ijkfi,j,k(MHz)λi,j,k(m)βionβn1763/590763/6204683.2940.0640131621.39563540.577823181114036.7580.074271.36270.581141012829.6180.1059481.2306450.71286360112475.6600.12109591.59149530.70732401102768.2380.10829721.29322030.7108766
从表1可以看出这些组合波长都小于B1的波长0.192m,放大了电离层的影响,减小了噪声的影响,当基线距离较短时,放大的电离层影响可以忽略,减小的相位噪声有利于定位精度的提高。
表2是三频常用的消电离层组合的特性,可以看到组合后虽然电离层比例因子为零,但是增加了相位噪声因子,不同的消电离层组合,相位噪声因子不同。
表2 三频消电离层组合特性

组合系数ijkfi,j,k(MHz)λi,j,k(m)βionβn10-620/763530.32159110.565300.03.52748651-590/7630627.66077850.477630.02.897870-590/6201119.79000002.502650.014.28626
对比表1和表2,组合(1,763/590,763/620)能满足短基线对最优组合的要求。
3.2 中长基线相对定位
对流层延迟和轨道误差不能通过线性组合得到减弱或消除,而电离层误差可以通过线性组合得到减弱或消除,因此,满足相位噪声最小的消电离层组合即为最优的线性组合。只要满足公式(8)定义相位噪声因子最小即为最优组合。
(8)
经推导可得满足相位噪声因子最小的组合系数表达式为:
(9)
令k=-1,将区域卫星导航系统的三个频率f1=1561.098,f2=1207.14,f3=1268.52MHZ代入公式(9),可得最优线性组合为(6.179, -3.826,-1),该观测组合的特性见表3。
表3 无电离层噪声最小组合特性

组合系数ijkfi,j,k(MHz)λi,j,k(m)βionβn6.179-3.826-13758.470760.07980.02.865
4 试验分析
4.1 短基线相对定位试验
短基线相对定位采用北斗实际数据进行试验。基线XX01- XX02,长为2.4785m,XX01坐标已知,观测时间为2013年05月15日,采样率为1s。在实数解部分,未知参数有21个,包括3个坐标分量改正数和18个双差模糊度参数,分别是卫星组合(2-1,4-1,5-1,6-1,8-1,9-1)的3频双差组合模糊度。流动站坐标和整周模糊度通过静态测量方法精确获取。
为了得到最优组合(1,763/590,763/620)与单独利用B1、无电离层组合(1,-590/763,0)等常规基线解算方法的定位精度比较结果,对以上三种组合分别进行基线解算,求解相邻500个历元的位置参数,位置误差分量的曲线图如图1~图3所示。对该500个历元的解算结果进行统计,表4列出了采用不同观测类型获得的点XX02的坐标偏差标准差。

图1 只采用B1频点解算的基线误差
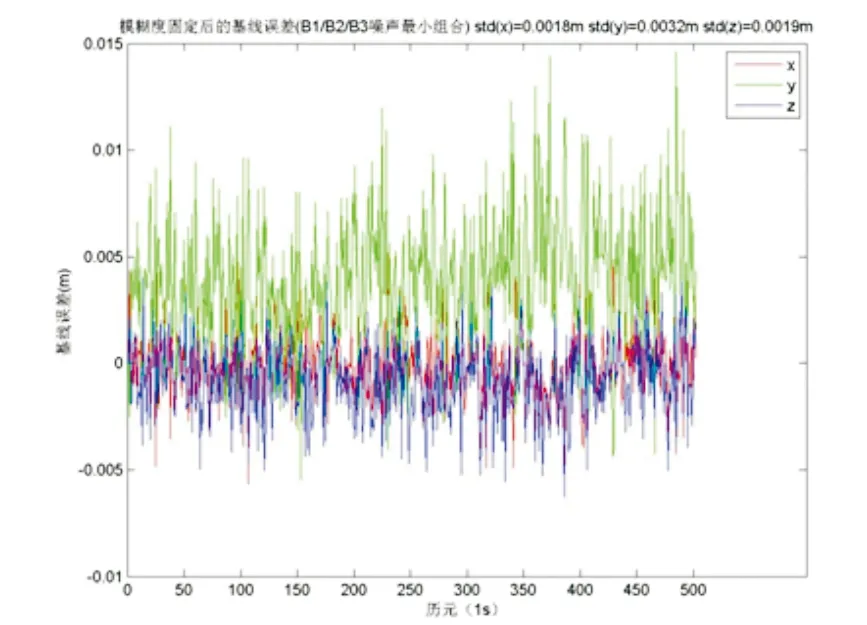
图2 采用B1/B2/B3噪声最小组合解算的基线误差
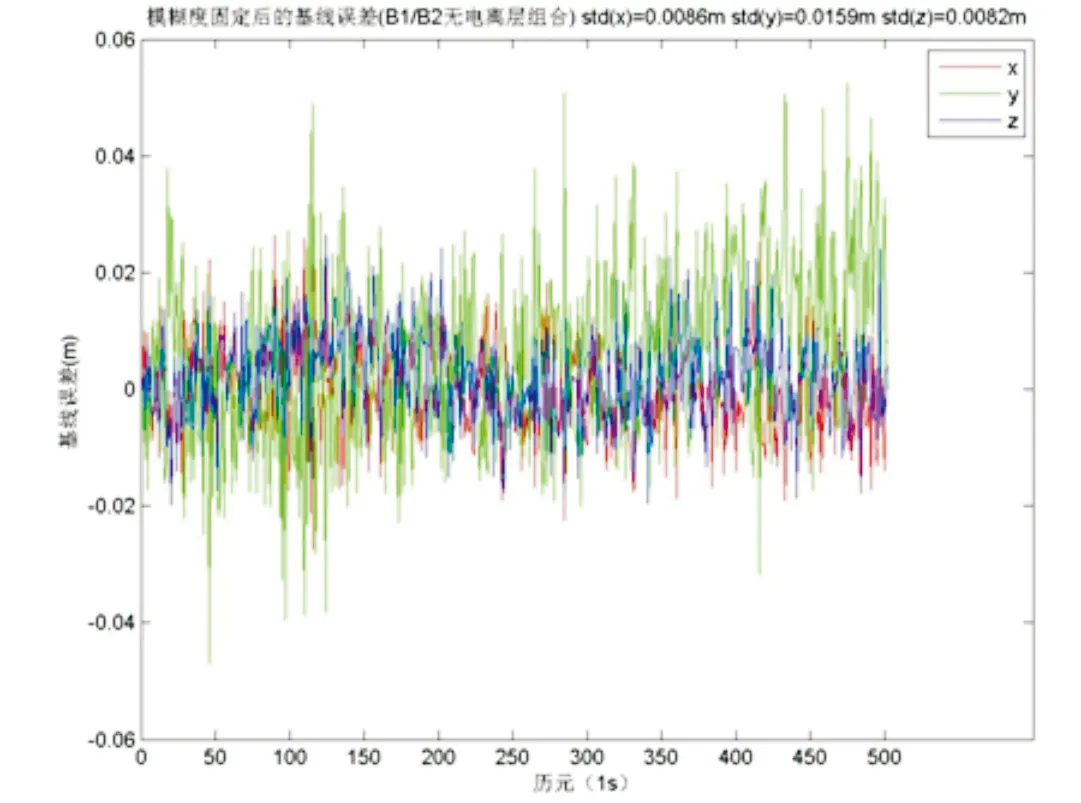
图3 采用B1/B2无电离层组合解算的基线误差
表4 点XX02坐标偏差标准差
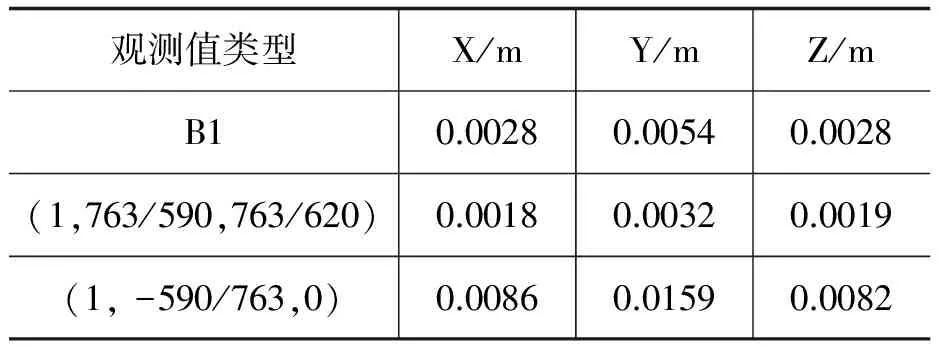
观测值类型X/mY/mZ/mB10.00280.00540.0028(1,763/590,763/620)0.00180.00320.0019(1,-590/763,0)0.00860.01590.0082
从表4可以看出,无电离层组合观测值(1, -590/763,0)解算精度最差,这是因为在短距离基线解算中,相位噪声为主要误差,形成无电离层组合时放大了相位噪声。组合观测(1,763/590,763/620)的解算精度比B1和无电离层组合都高,在短基线的情况下是最优组合。
4.2 中长基线相对定位试验
中长基线相对定位采用北斗仿真数据进行试验。首先输入卫星轨道和接收机坐标两个基本量,由此可以得到卫星与接收机之间的几何距离,在此基础上加入各类误差改正项即可获取仿真观测量。模拟数据时采用了Klobuchar模型近似地描述地球上任何经度、纬度及任何时刻的垂直电离层折射影响,对流层模型采用Black模型模拟天顶方向的对流层延迟,观测数据噪声采用高斯白噪声模型,具体仿真过程参见文献[7]。
基线YY01-YY02,长度约为559.812km, YY01坐标已知。设在相对定位前,三个原始频率上的模糊度已正确固定,利用已知的模糊度求解前160个历元的位置参数。图4和图5分别是只用B1观测量进行定位的误差曲线图和利用无电离层且噪声最小的观测组合进行定位的误差曲线图。
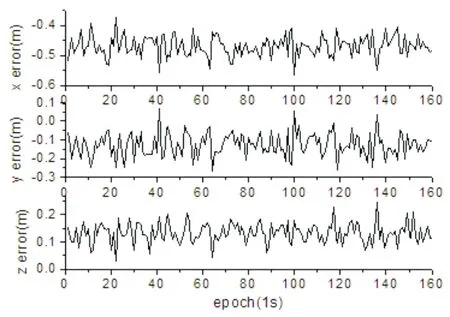
图4 长基线B1定位误差
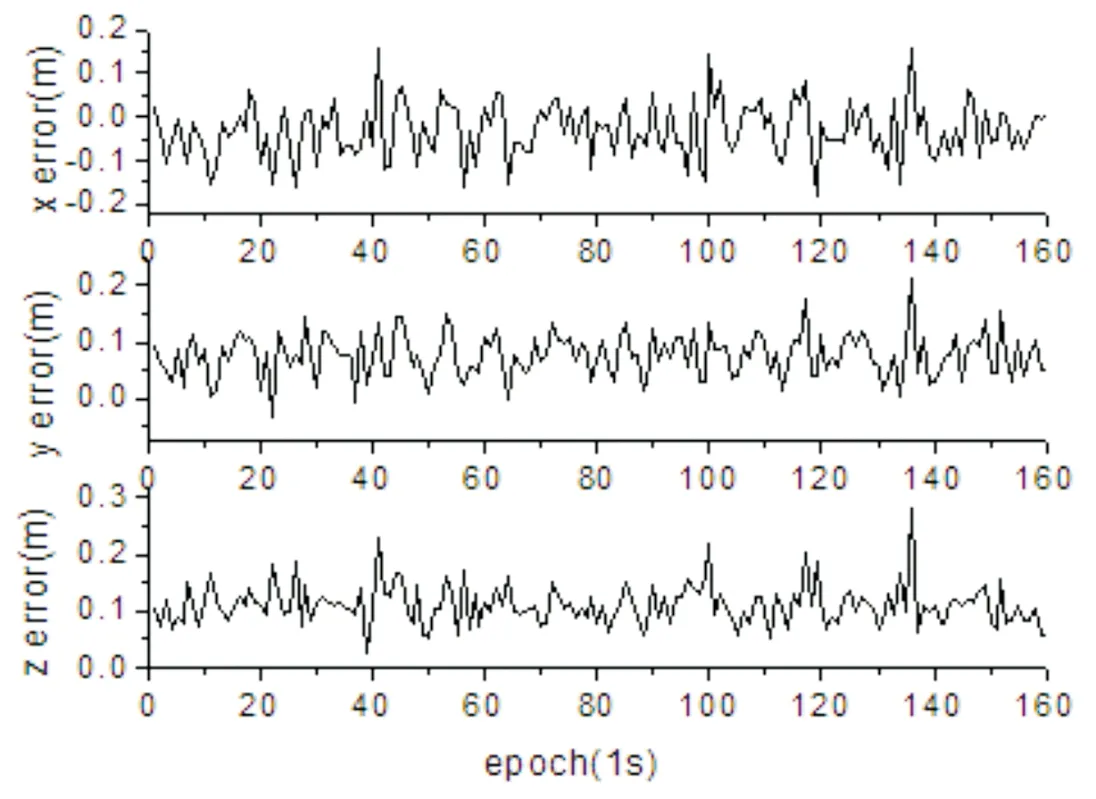
图5 长基线最优组合定位误差
对比以上两图可以得出,只利用B1相位观测量进行相对定位精度低于利用噪声最小的无电离层组合的相对定位精度,原因是前者没有改正电离层误差;后者经过最优组合改正了影响定位精度的最主要误差源电离层误差,然而相对定位误差在X、Y、Z方向上仍然较大,原因在于最优组合无法消除轨道误差和对流层延迟误差。
5 结 论
区域卫星导航系统具有三个频率的相位观测量,通过观测量之间的线性组合可以使电离层误差得到减弱或消除,也可能带来相位噪声的增大或减小。本文以提高相对定位精度为目的,以减弱相位噪声和电离层延迟误差为手段,分别针对短基线和中长基线模型,从理论上推导了相对定位的最优线性组合,并结合实测和仿真数据,验证了最优线性组合的相对定位结果高于其他组合观测量的结论。
[1]韩绍伟.GPS组合观测值理论及应用[J].测绘学报,1995,24(2):8-13.
[2]何海波.高精度GPS动态测量及质量控制[D].郑州:信息工程大学,2002.
[3]魏二虎,黄劲松.GPS测量操作与数据处理[M].武汉:武汉大学出版社,2004.
[4]Han S, Chris Rizos C. The Impact of Two Additional Civilian GPS Frequencies on Ambiguity Resolution Strategies[C].55th National Meeting U.S. Institute of Navigation, Cambridge, 1999.
[5]RICHERT T, EI-SHEIMY N. Optimal Linear Combinations of Triple Frequency Carrier Phase Data from Future Global Navigation Systems[J]. GPS Solution, 2007(11):11-19.
[6]International GNSS Service(IGS), RINEX Working Group and Radio Technical Commission for Maritime Services Special Committee 104(RTCM-SC104)[S]. RINEX The Receiver Independent Exchange Format Version 3.02,2013.
[7]常志巧.COMPASS卫星导航系统精密相对定位理论及其应用研究[D].郑州:信息工程大学,2009.
Analysis of the Optimal Linear Combination of Triple Frequency Carrier Phase for BDS
Chang Zhiqiao1,2,Cao Jidong1,Dong Enqiang1
1. Beijing Satellite Navigation Center,Beijing 100094,China 2. Shanghai Astronomical Observatory,Shanghai 200030,China
BDS is qualified with triple frequency phase observations, which not only have advantages in cycle-slip detecting and ambiguity resolving, but also have the ability to improve the relative positioning accuracy. Assuming that the ambiguities have been resolved correctly, the paper deduces the optimal linear combination of frequencies for the short baseline relative positioning with the minimum noise. Besides, the paper deduces the optimal linear combination of frequencies for the medium-long baseline relative positioning with elimination of influence of ionosphere, which can be thought that the main error is ionosphere delay in the double differences observation. The experiments and simulation calculations show that the relative positioning accuracy for the optimal combination is higher than those of other observation combinations.
BDS(BeiDou Satellite Navigation System); relative positioning; carrier phase observation; the optimal combination; short baseline ; medium-long baseline
2014-11-19。
上海市空间导航与定位技术重点实验室开放课题基金资助项目(201105)。
常志巧(1981—),女,工程师,主要从事卫星导航数据处理研究。
P
A

