解析Brown模型波形参数的最小二乘估计

翟振和，李晓燕

1.西安测绘研究所，陕西 西安，710054；2.地理信息工程国家重点实验室，陕西 西安，710054；3.测绘导航局，北京，100045



解析Brown模型波形参数的最小二乘估计

翟振和1,2，李晓燕3

1.西安测绘研究所，陕西 西安，710054；2.地理信息工程国家重点实验室，陕西 西安，710054；3.测绘导航局，北京，100045

Brown回波模型是描述传统雷达高度计的基本模型，它对于获取高精度的海面高具有重要作用。本文在解析Brown模型的基础上，推导获得了最小二乘估计中关于五个波形参数的具体公式。在相同的仿真数据条件下，以海面高改正值为比较对象，通过与中科院空间中心的计算结果比较，表明其互差在mm级。

卫星测高；解析Brown模型；波形重跟踪；最小二乘估计

1 引 言

波形重跟踪(waveformretracking)是海洋测高卫星数据处理中的一项关键技术，其本质是通过回波波形获取高精度海面高、海浪高、风速等地球物理参数[1]。基于微波散射理论，Moore和Williams(1957)以及Barrick(1972)阐明了对于一个粗糙的散射面，平均回波功率作为时间延迟的函数可以表示为三部分的卷积即平面脉冲响应函数、镜像点高程的概率密度函数以及雷达系统点目标响应。Brown(1977)在前人研究的基础上构建了平均回波功率的卷积表达式，即Brown模型。除了利用Brown模型估计回波参数外，国内外学者还利用重心偏移重跟踪算法即OCOG算法(OffsetCentreofGravityRetracker)、β参数法、阈值法、改进阈值法等对T/P、ERS-1、Envisat、Geosat等测高卫星开展了波形重跟踪计算与分析，获得了大量有价值的结论和研究成果[2-9]。虽然目前波形重跟踪方法很多，但从理论上分析，基于Brown模型的波形参数估计仍是最严密的方法；从工程实际考虑，这种方法也是目前主流测高卫星(如Jason-1、Jason-2)采用的方法[10]。目前，在关于Brown模型应用的文献中，都没有给出利用Brown模型进行波形参数估计的具体过程。为此，本文将基于简化的解析Brown模型，给出回波波形五个参数的具体估计过程，并利用仿真数据进行检核。

2 解析Brown模型

Brown模型的基本形式如下：

P(t)=Pfs(t)*qs(t)*Pptr(t)

(1)

式中，P(t)表示回波波形能量；t表示时间；Pfs(t)表示平坦海面的冲击响应；qs(t)是镜像点的海洋面高程概率密度函数；Pptr表示雷达点目标响应。上式是一个卷积表达式，为了实际应用需要进行简化，当忽略海面高度倾斜参数影响后，Brown模型可得到如下简化形式[11]：

(2)

式中，A0表示信号幅度；erf表示误差函数；PN表示热噪声水平；ζ表示偏天底点角。式中τ、d分别表示如下：

(3)

(4)

式中，γa表示天线波束宽度参数；c表示光速；h表示卫星相对于参考椭球高度；R表示地球半径；σ表示上升时间。式(2)中包含了描述回波波形基本特征的5个参数，它们分别是：

①t0：表示对应于平均海水面的时间偏移；

②σ：表示合成上升时间，由此参数可获得有效波高；

③A0：信号幅度，由此参数可获得后向散射系数；

④PN：表示热噪声水平；

⑤ζ：偏天底点角。

对于测高应用，我们更关注海面高的确定，而根据参数t0就可获得海面高的精密改正值ds。

ds=tp·c/2·(t0/tp-g0)

(5)

式中，tp表示雷达脉冲宽度；c表示光速；g0表示高度计正常跟踪点所在的门数。

3 解析Brown模型参数的迭代最小二乘估计

目前，参数估计的方法主要有极大似然估计(MLE)和最小二乘估计等方法，本文采用迭代最小二乘法进行求解五个参数，具体模型如下：

V=MAδx-L

(6)

式中，δx表示待估参数改正值；MA表示P(t)对待估参数的偏导数在初始值x0时形成的矩阵；V表示残差；L表示P(t)的观测值即高度计回波波形。

L=PL-P(x0)

(7)

式中，PL表示观测得到的回波波形；P(x0)表示利用待估参数初始值计算得到的回波波形。利用最小二乘原理得到待估参数改正值

(8)

式中，PW表示观测值的权。

为了进行参数估计，首先应给出待估参数的初始值，初始值的选取分别如下：

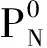
(9)

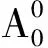
(10)

式中，N表示高度计回波波形的总门数。文中，n1=n2=4。

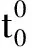
(11)

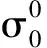
(12)

式中，ft是利用高斯函数估计压缩脉冲形状的值；SWH表示有效波高，文中取值为4m。

其次，需要求出P(t)关于各参数的偏导数。

则各参数偏导数推导如下:

(13)

(14)

(15)

(16)

式(15)、式(16)中各偏导数推导如下：

(17)

(18)

(19)

(20)

式中，ζ的初值选为0，但由于当ζ趋向于0时，其偏导数也趋向于0，因此，为了避免无法估计ζ的问题，实际解算中以ζ2代替ζ进行估计。关于ζ2偏导数的推导如下：

(21)

考虑到sinζ与ζ在ζ很小时量级一致，则有：

(22)

由u和v表达式可得：

(23)

(24)

对于观测值权Pw的确定采用两种方式：一种是等权处理；一种是参考ERS-2卫星的定权原则如下：

Pwi=200 i≤LEG-1

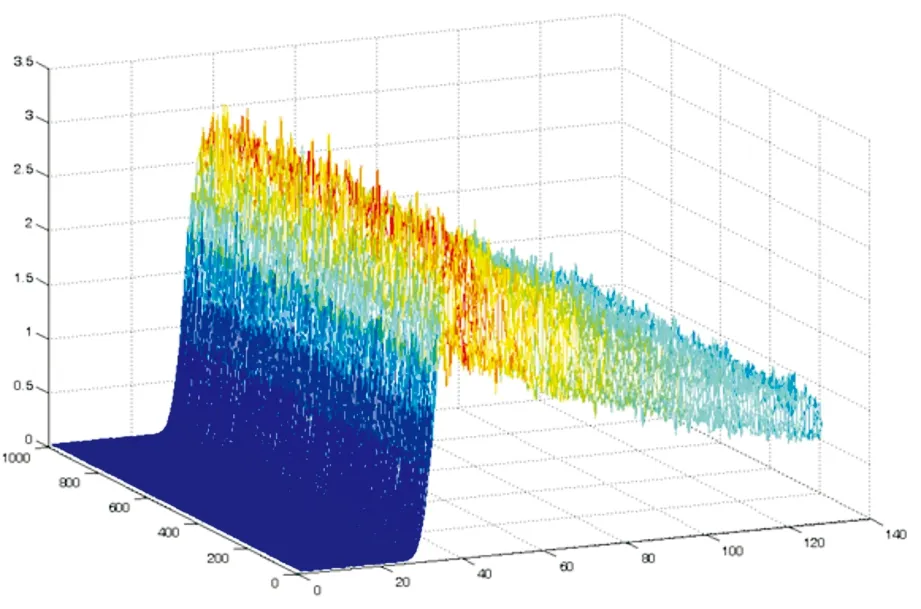
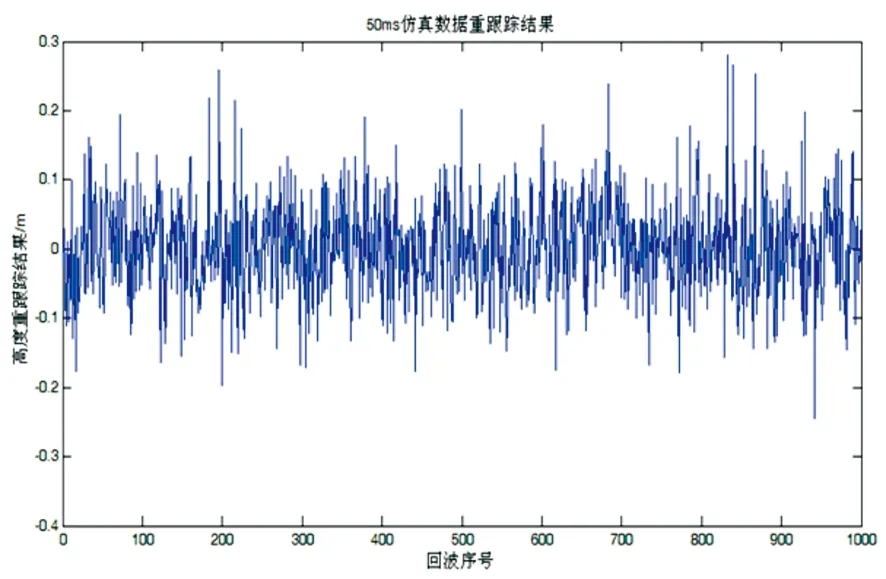
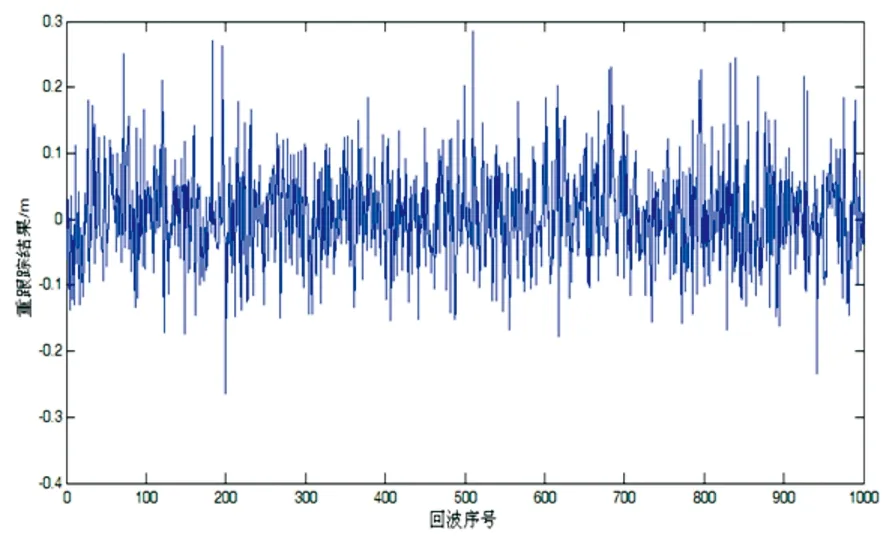
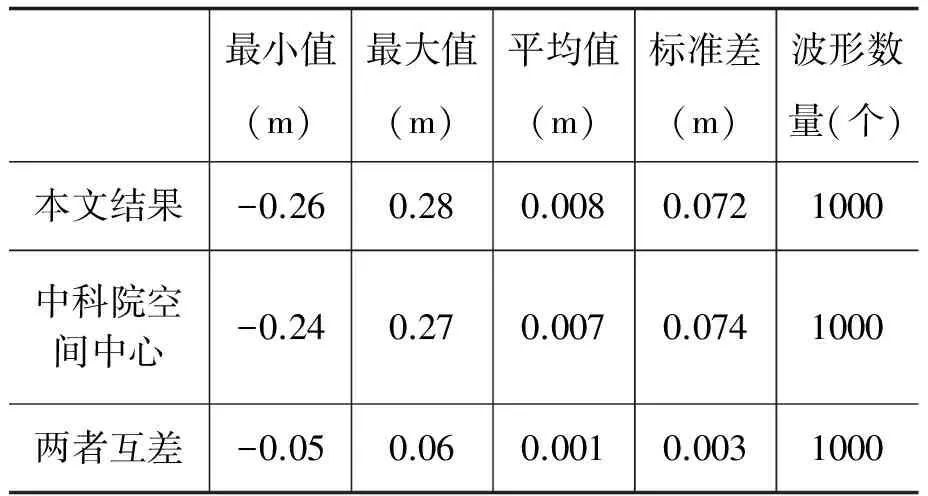
Pwi=100LEG-1

Pwi=50LEG+2

(25)

式中，LEG表示波形前缘位置，N表示波形门数。

4 波形参数最小二乘估计的仿真试验

为了验证本文推导公式的准确性，采用另一单位中科院空间中心的仿真试验进行比对(采用Jason-1卫星简化的Brown模型)。仿真数据生成的条件是：4m有效波高，回波幅度平均2.5，姿态角为0，128门值，正常跟踪点33，轨道高度960km，天线波束宽度1.2°，点目标相应采用高斯函数，波形频率是20Hz。仿真的高度计回波波形如图1所示。

图1 仿真波形数据

为了便于比对，选取海面高改正值(t0)作为比较对象，两个单位的波形重跟踪结果如图2和图3所示。

图2 中科院空间中心重跟踪结果

图3 基于本文算法的波形重跟踪结果

实际计算中，迭代的次数一般不超过5次就能收敛，且等权处理与按式(24)加权处理的结果基本一致，图3所示为不加权的结果。两个单位计算结果的统计情况见表1。

表1 仿真数据波形重跟踪结果统计

最小值(m)最大值(m)平均值(m)标准差(m)波形数量(个)本文结果-0．260．280．0080．0721000中科院空间中心-0．240．270．0070．0741000两者互差-0．050．060．0010．0031000

通过图2、图3及表1可以看出，本文计算结果与中科院空间中心计算结果非常一致，差异在mm级，这也验证了本文对基于Brown模型的参数估计的公式推导是可信和准确的。

5 结 语

为了实现利用Brown模型进行波形重跟踪，本文在解析Brown模型基础上，推导获得了最小二乘估计中关于五个波形参数的具体公式，以海面高改正值为比较对象进行了仿真试验比对。统计结果表明，最小二乘估计迭代的次数一般不超过5次就能收敛，等权与不等权的结果基本一致，本文结果与中科院空间中心的计算结果的互差在mm级，从而验证了文中公式的准确性。为了进一步验证本文所推导的公式，需要结合实测波形数据进行更全面的比对。

[1]S.Vignudelli,A.Kostianoy,P.Cipollini.CoastalAltimetry[M].Springer-VerlagBerlinHeidelberg,2011.

[2]鲍李峰，陆洋，许厚泽．浅海区域Topex/Poseidon测高卫星数据波形重构方法[J]．地球物理学报，2004，47(2)：216- 221．

[3]常晓涛，李建成，郭金运等．一种多前缘多阈值的波形重构算法[J]．地球物理学报， 2006，49(6)：1629-1634．

[4]杨乐，林明森，张有广等．中国近岸海域高度计JASON-1测量数据的波形重构算法研究[J]．海洋学报，2010，32(6)：91-101．

[5]郭金运，高永刚，常晓涛等．近岸海域ENVISAT卫星测高波形重定的Threshold优化算法[J]．地球物理学报，2010，53(4)：807-814．

[6]杨元德,鄂栋臣,黄金维等.Geosat/GM波形重跟踪反演中国沿海区域重力异常[J]. 武汉大学学报·信息科学版,2008,33(12):1288-1290.

[7]褚永海,李建成,张燕等.ENVISAT测波形重跟踪分析研究[J].大地测量与地球动力学，2005,25(1):77-79.

[8]DavisCH.Arobustthresholdretrackingalgorithmformeasuringice-sheetsurfaceelevationchangefromsatelliteradaraltimeter[J].IEEETransGeosciRemoteSensing，1997，35(4):974-979.

[9]HwangC,GuoJY.CoastalgravityanomaliesfromretrackedGeosataltimetry:improvement,limitationandtheroleofairbornegravitydata[J].JGeod，2006(80):204-216.

[10]HyongkiLee,C.K.Shum,WilliamEmery.ValidationofJason-2altimeterbywaveformretrackingovercoastalocean[J].MarineGeodesy,2010(33)：304-316.

[11]XiaoliDeng.ImprovementofGeodeticParameterEstimationinCoastalRegionsfromSatelliteRadarAltimetry[D].DoctorofPhilosophy,CurtinUniverstiyofTechnology,2003.

Least Square Estimation of Waveform Parameters of Analytical Brown Model

Zhai Zhenhe1,2,Li Xiaoyan3

1.Xi’an Research Institute of Surveying and Mapping, Xi’an 710054, China 2.State Key Laboratory of Geo-information Engineering, Xi’an 710054, China 3.Agency of Surveying,Mapping & Navigation,Beijing 100045, China

The Brown waveform model is the basic one that describes the traditional radar altimeter, which is critical to obtain high accuracy sea surface height. Based on the analytic Brown model, the paper derives partial derivatives for five waveform parameters. Using the same simulation data, the paper compares the sea level height correction value to the results from Space Centre of Chinese Academy of Sciences, and it shows that the differences are in the order of millimeters.

satellite altimetry; analytical Brown model; waveform retracking; least square estimation

2014-12-30。

高分专项青年创新基金资助项目(GFZX04060103-7-14)。

翟振和(1980—)，男，助理研究员，主要从事物理大地测量研究。

P228

A