顾及测距系统误差的星地/星间联合定轨

张 博，贾小林，陈 虓，毛 丽

1．信息工程大学地理空间信息学院，河南 郑州，450052;2．西安测绘研究所，陕西 西安，710054;3．西安卫星测控中心，陕西 西安，714043;4．91039部队，北京，102401



顾及测距系统误差的星地/星间联合定轨

张 博1，2，贾小林2，陈 虓3，毛 丽4

1．信息工程大学地理空间信息学院，河南 郑州，450052;2．西安测绘研究所，陕西 西安，710054;3．西安卫星测控中心，陕西 西安，714043;4．91039部队，北京，102401

利用仿真星间链路测距数据并加入±75cm的白噪声和60cm的系统误差，参考地面站观测数据仿真星地观测数据，依据星地/星间联合定轨原理，进行联合定轨解算，并讨论了星间测距系统误差对联合解算结果的影响。试验证明， 1天弧长观测数据下，用上述方法解算，将结果和精密星历比较，联合定轨结果好于仅使用地面站观测数据的解算结果；当顾及星间测距系统误差后，卫星轨道在沿切向、法向、径向上残差平均值均小于5mm。

系统误差；轨道；星间链路；联合

1 引 言

星间链路可以帮助卫星导航系统实现自主定轨，在战时维持系统的生命力，在非战时还可以综合利用地面观测站数据和星间测距数据实现星地/星间联合定轨[1-5]。但在联合解算时，若星间测距信号和下行导航信号设备时延不一致，将会以系统误差的形式影响解算结果[6]。

目前，由于各卫星导航系统星间链路数据暂时无法获得，对于星地/星间联合定轨的研究大多是通过仿真数据来进行，且有的忽略设备时延的存在，有的仅考虑小量级的设备时延误差，因而没有对此类系统误差进行深入研究[7-9]。本文利用仿真手段生成星间测距数据，在联合地面仿真观测站数据进行星地/星间联合定轨解算同时，对此系统误差进行解算，最后将解算轨道结果与精密星历比较。试验表明，此方法可以在一定程度上改善定轨结果。

2 数据仿真

2.1 星间测距数据仿真

由精密星历可以得到卫星位置信息，知道了卫星的位置后，参考“可视即可测”模型，可仿真生成星间测距数据。如图1所示，假设有两颗卫星A和B，卫星间距离为dc，间隔角度为γs，Re为地球半径，H为电离层高度取1000km[10]，则

(1)

两颗卫星的最大可视距离为两颗卫星之间连线与地球表面相切，即

(2)

两颗卫星的最小可视距离取间隔角度γs=1°时的情况。

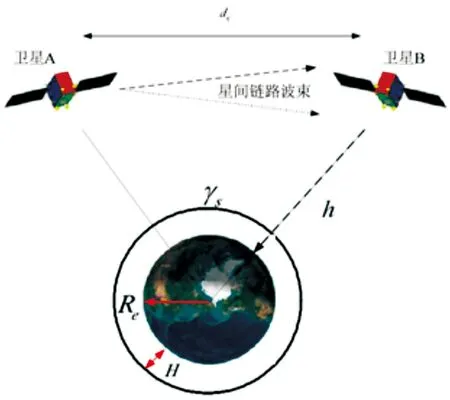
图1 星间链路可视距离

仿真时，卫星天线波束角范围选为75°。首先根据T时刻两卫星位置计算dc，然后由距离dc/光速计算信号在两卫星间传播所需的时间t1，再插值计算T-t1时刻信号发射卫星位置，信号接收卫星位置不变，由新dc计算新的传播时间t2，重复此过程，直到|(ti-ti+1|≤10-9，结束迭代，发射时刻为T-ti+1，接收时刻为T。观测量系统差设为60cm，噪声参照GPSBLOCKIIR卫星的星间测距观测噪声，设为±75cm[11]。经仿真，单颗星平均每个历元可接收到24条星间测距数据。

2.2 星地观测数据仿真

通过精密星历得到卫星在各历元时刻的位置信息后，根据各站点观测数据文件中对应历元时刻观测站所观测到的卫星关系，同星间数据仿真，迭代计算卫星与地面站之间观测数据。

3 星间数据处理

在处理星间观测数据时，对仿真获得的距离观测值，需要进行预处理。由于不考虑电离层时延误差、多路径效应误差和相对论效应改正等[12]，所以在仅考虑系统误差存在的情况下直接对星间观测数据做归化处理。

假设导航星座中任意2颗通视卫星i、j进行相互观测，设ρij、ρji为改化至某一参考历元的伪距观测值，则改化后的观测方程可简写为：

(3)

(4)

式中，i、j为卫星号；x、y、z为卫星的坐标值；δt为卫星的钟差，单位为m；β为卫星的系统误差；ε为卫星星间测距的随机误差。

在解算时，可通过(3)、(4)式互加或互减将轨道参数和钟差参数分开求解；也可采用统一求解的方法，将轨道和钟差参数一起求解[12]。本文选用了后者。

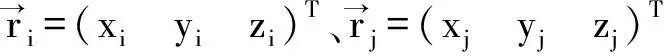
Vij=(-AijAij1 -1 1 1)·H-lij

(5)

Vji=(Aij-Aij1 -1 1 1)·H-lji

(6)

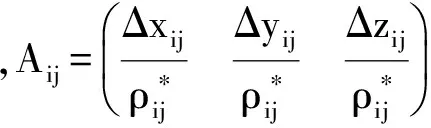
H=(δxiδyiδziδxjδyjδzjδtiδtjβiβj)T。

利用状态转移矩阵将某一历元时刻卫星位置修正值表示为初值修正值，形式为：

(7)

(8)

式中，δX为初值修正值；Ψ(t,t0)为状态转移矩阵。

根据(5)、(6)式，以初值为待估参数，则卫星i、j之间的距离观测方程为：

(9)

采用最小二乘方法组合星地/星间观测方程进行定轨参数估计。

4 仿真实验与结果分析

4.1 解算模型

试验采用自编软件进行星地定轨、星地/星间联合定轨解算。解算中所用到的模型见表1。

表1 定轨解算模型

参 数模 型观测量星地伪距、载波相位观测值，星间测距观测值采样间隔5min地球重力场模型10阶EGM96三体引力日、月引力潮汐摄动固体潮光压模型BERN5参数(D0、Y0、B0、BC、BS)积分器Runge-Kutta起步，Adams-Moulton多步法预报校正估计器标准最小二乘法

4.2 实验说明

取2014年8月20日BJFS、CHAN、KUNM、LHAZ、SHAO、URUM、XIAN共7个分布在我国的IGS观测站单天的观测数据和当天精密星历作为实验数据，站点分布如图2所示。

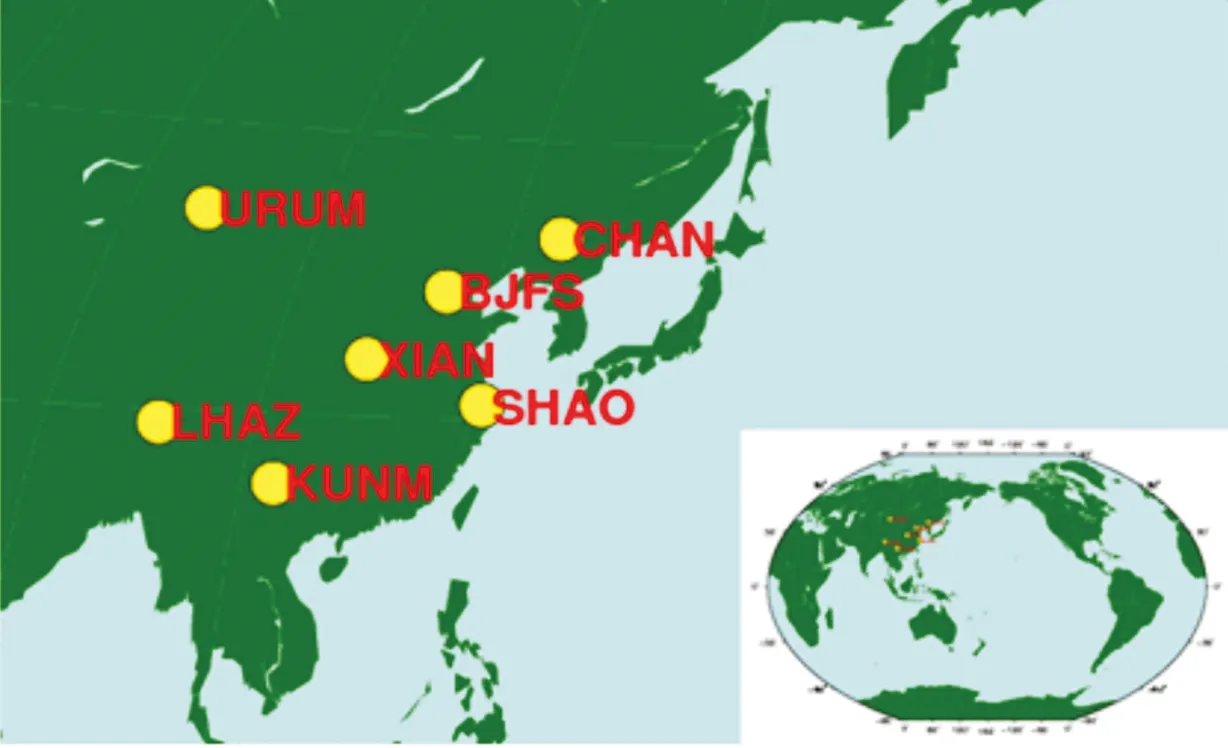
图2 实验用IGS站点分布图

试验在星地/星间联合定轨中分顾及、不顾及系统误差影响两种方案，同时以单纯利用星地观测数据定轨结果作为参考，以上三种定轨结果与精密星历比较。其中，星地数据同时取伪距和载波相位，星间仅有伪距数据。

4.3 星地与星地/星间联合定轨结果比较

按试验说明做定轨解算后，为了轨道之间比较，统计了轨道在A(alongdirection，切向)、C(crossdirection，法向)、R(radialdirection，径向)三方向残差和用户距离误差URE。其中，URE计算公式如下[13]：

(10)

式中，δt为卫星钟差的确定误差。

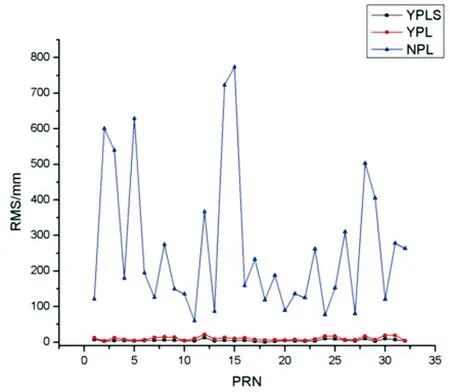
图3 定轨结果在A方向残差比较

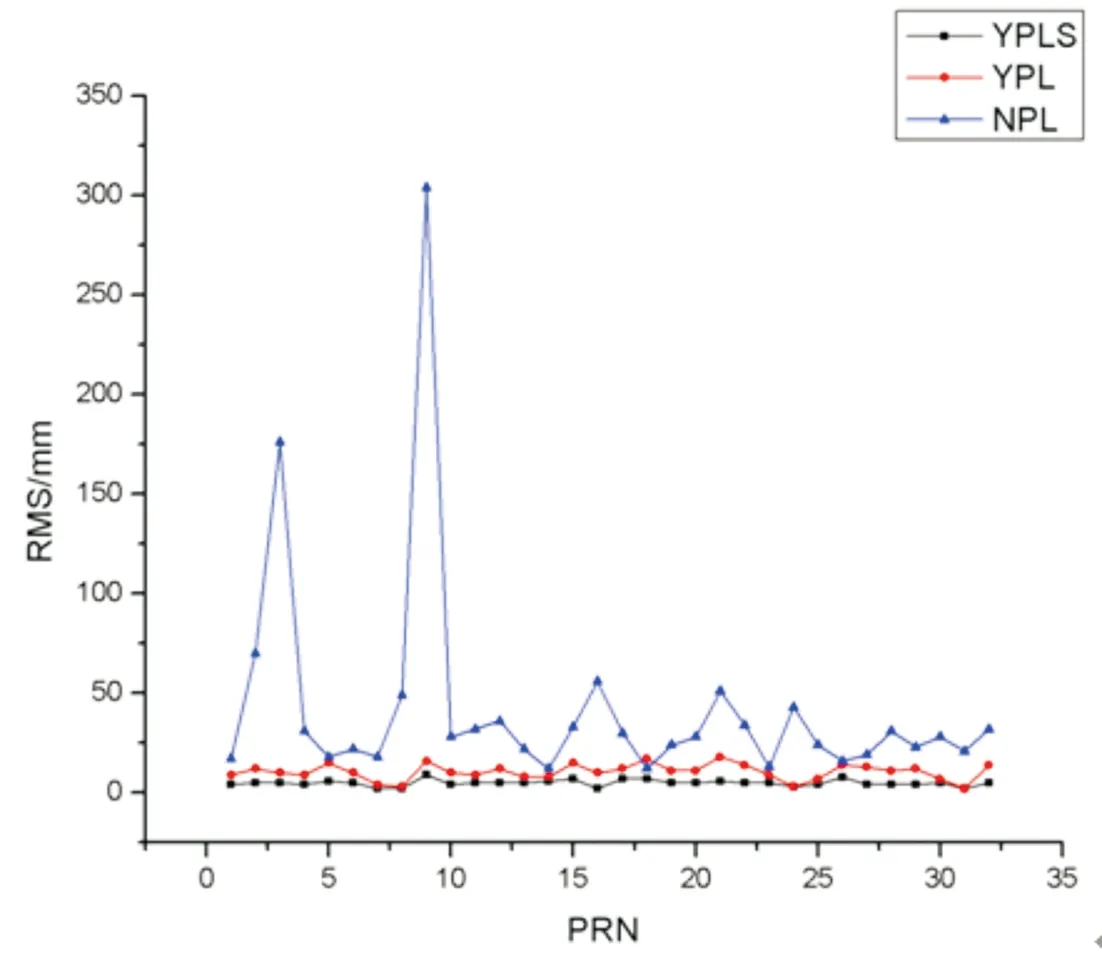
图4 定轨结果在C方向残差比较

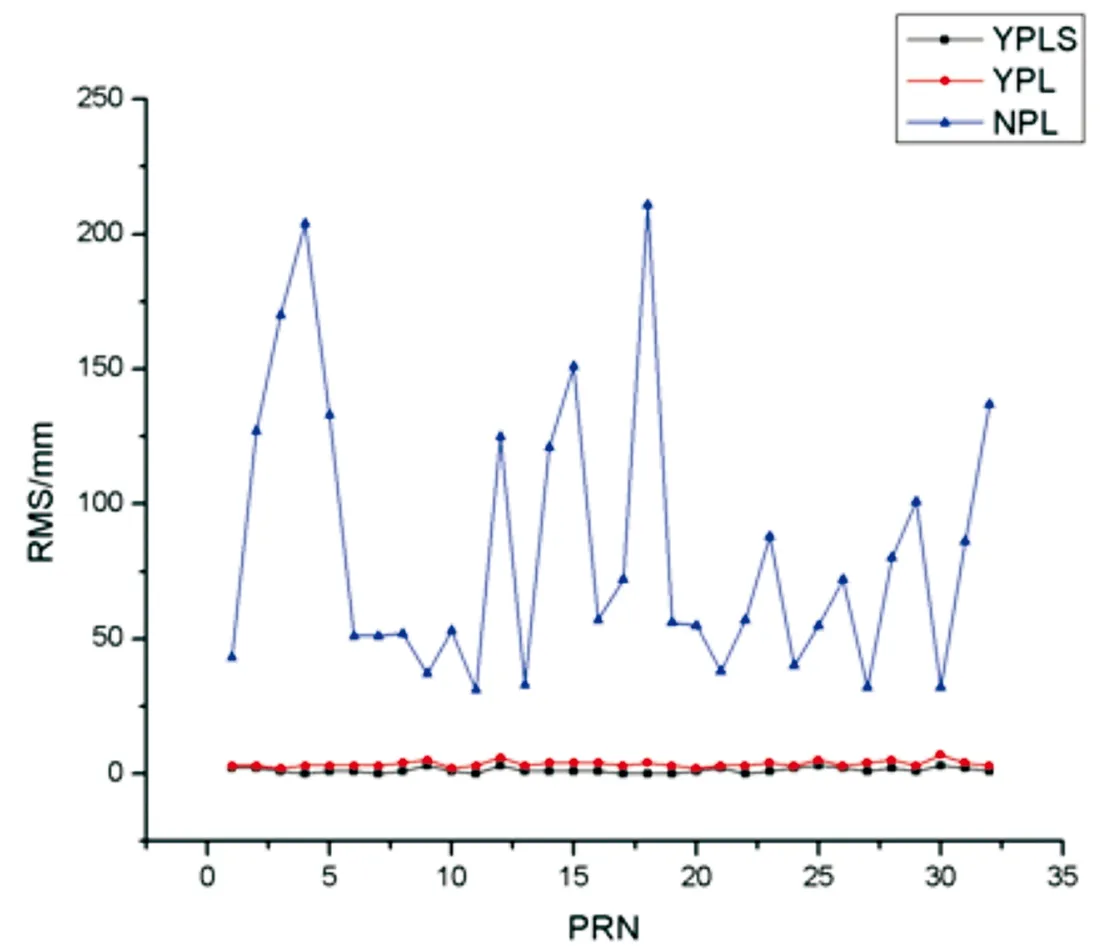
图5 定轨结果在R方向残差比较

表2 定轨结果残差统计(单位：mm)

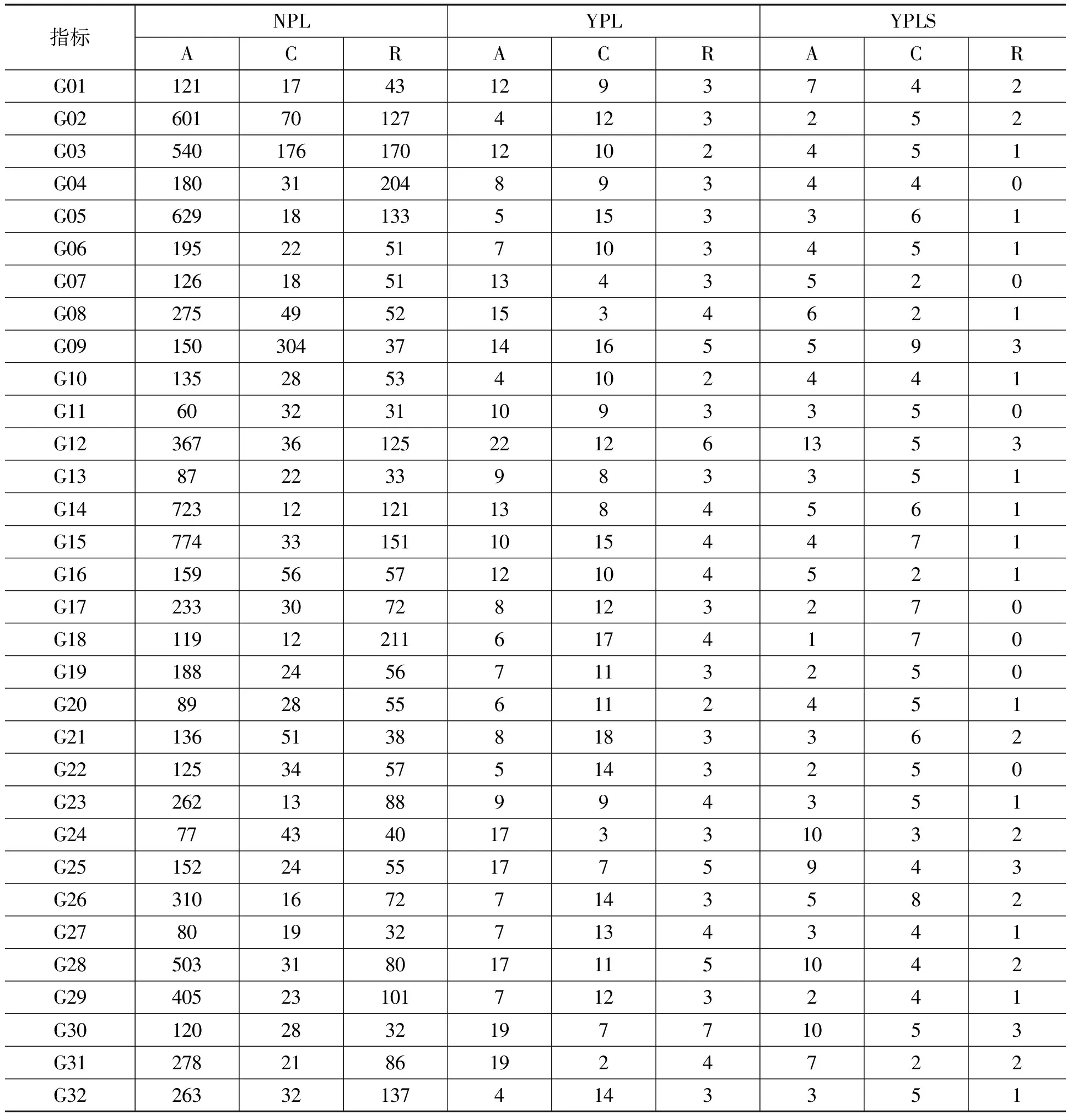
指标NPLYPLYPLSACRACRACRG0112117431293742G02601701274123252G0354017617012102451G0418031204893440G05629181335153361G0619522517103451G0712618511343520G0827549521534621G091503043714165593G1013528534102441G116032311093350G1236736125221261353G13872233983351G14723121211384561G157743315110154471G16159565712104521G1723330728123270G18119122116174170G1918824567113250G208928556112451G2113651388183362G2212534575143250G232621388994351G2477434017331032G2515224551775943G2631016727143582G278019327134341G285033180171151042G29405231017123241G30120283219771053G3127821861924722G32263321374143351

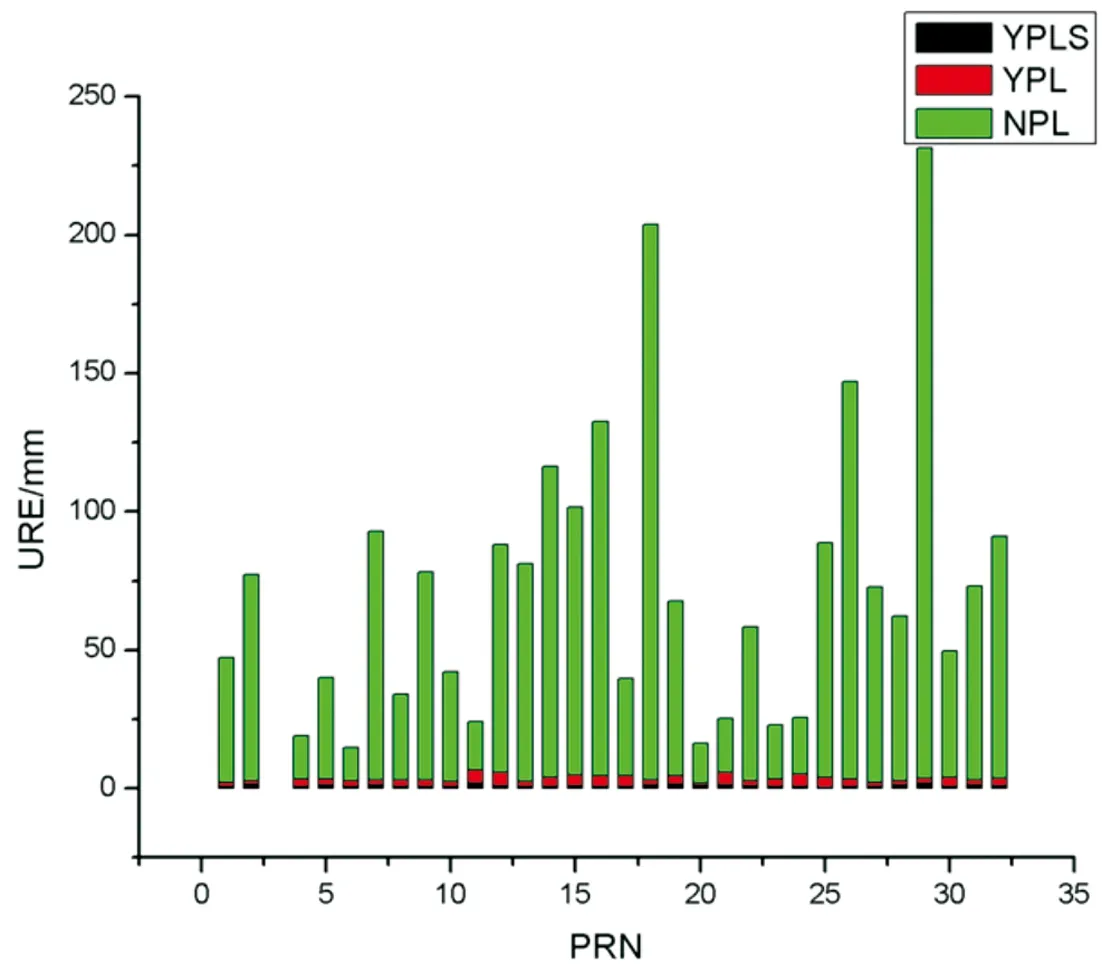
图6 用户距离误差比较

图3～6中，YPLS代表顾及系统误差的星地/星间联合定轨轨道比较结果，YPL代表未顾及系统误差的星地/星间联合定轨轨道比较结果，NPL代表星地定轨轨道比较结果。

从上图表可以看出，在A、C、R三个方向上，顾及了系统误差的联合定轨结果均好于未顾及系统误差和单纯星地定轨结果，且结果均值在5mm；星地/星间联合定轨的结果均远远好于仅考虑星地观测数据的星地定轨结果。

由图6和表3可以看出，星地/星间联合定轨的URE结果明显好于仅考虑星地观测数据的情况，顾及系统误差后的联合定轨URE最小。

表3 URE均值比较(单位：mm)

精度指标UNPLUYPLUYPLSURE均值96．574．211．82

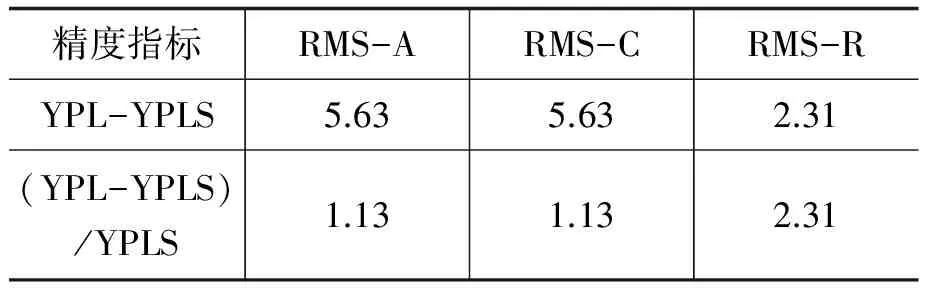
表4 残差均值互差值(单位：mm)

精度指标RMS-ARMS-CRMS-RYPL-YPLS5．635．632．31(YPL-YPLS)/YPLS1．131．132．31

表4是顾及与未顾及系统误差的联合定轨结果在A、C、R三个方向上定轨残差互差结果。可以看出，在顾及系统误差后，A和C方向上结果修正较大，R方向上结果修正相对较小，但在R方向上的改善最为明显。

5 结 语

本文对星地/星间联合定轨方法做了论述，通过实验，可以看出，星地/星间联合定轨可以改善定轨结果，当顾及系统误差后，结果有明显提高。所以，在进行联合定轨时，系统误差必须考虑。由于本文在用星间测距数据联合定轨时，对于星间测距数据，未针对系统误差做深入的细分，若进一步深入，可能更有益于定轨精度改善。

[1]Ananda M P, Bernstein H, Cunningham K E, etal. Global Positioning System Autonomous Navigation[J]. IEEE, 1990: 497-508.

[2]Martoccia D, Bernstein H. GPS Satellite Timing Performance Using the Autonomous Navigation(Autonay)[C]. The 11th International Technology Meeting of the Satellite Division of the Institute of Navigation, Nashville, tennessee, virgina, 1998.

[3]Rajan J A. Highlights of GPS II-R Autonomous Navigation[C]. ION 58th Annual Meeting and CIGTF 21st guidance Test Symposium, New Mexico, Virgina, USA, 2002.

[4]刘万科, 李征航, 龚晓颖. 潮汐摄动对导航卫星自主定轨中的星座整体旋转误差的影响分析[J]. 武汉大学学报·信息科学版, 2009, 34(12)：1394-1398.

[5]刘万科, 龚晓颖, 李征航等. 综合星间和地面测距数据的导航卫星联合定轨[J]. 武汉大学学报·信息科学版, 2010, 35(7)：1811-1815.

[6]阮仁桂，冯来平，贾小林. 导航卫星星地/星间链路联合定轨中设备时延估计方法[J]. 测绘学报，2014, 43(2): 137-142, 157.

[7]耿涛，刘经南，赵齐乐等. 星地监测网下的北斗导航卫星轨道确定[J]. 测绘学报, 2011, 40(增刊): 47-51. [8]刘万科，龚晓颖，张卫星. 联合地面实测数据与星间模拟数据的GPS精密定轨[C].CSNC 2011论文集,上海, 2011.

[9]蔡志武，韩春好，杜燕等. 利用星地和星间链路的轨道测定方法及精度分析[C].CSNC 2011论文集,上海, 2011.

[10]朱俊. 基于星间链路的导航卫星轨道确定及时间同步方法研究[D].长沙：国防科学技术大学, 2011.

[11]Rajian J A,Brodie P,Rawicz H. Modernizing GPS Autonomous Navigation with Anchor Capability[C].ION GPS/GNSS 2003,Portland,2003.

[12]熊永清, 贾沛璋. 星载GPS自主定轨的长期稳定性[J]. 天文学报, 2006, 47(4)：467-474.

[13]Ananda M P,Bernstein H,Cunningham K E,etal. Global Positioning System Autonomous Navigation[J].IEEE,1990:497-508.

Combined Orbit Determination Using Satellite-ground and Inter-satellite Observations with Systematic Errors in Distance Measurements

Zhang Bo1,2, Jia Xiaolin2, Chen Xiao3, Mao Li4

1. Institute of Geospatial Information, Information Engineer University, Zhengzhou 450052 , China 2. Xi’an Research Institute of Surveying and Mapping, Xi’an 710054,China 3. Xi’an Satellite Control Center, Xi’an 714043, China 4. Unit 91039, Beijing 102401, China

Based on the simulation inter-satellite link observation data, with introduction of white noise of±75cm and systematic errors of 60cm in distance measurements, the paper deals with the combined orbit determination by using simulation satellite-ground observation. Besides, the paper discusses the impact of inter-satellite ranging system errors on the combined orbital determination. The experiment demonstrates that using the observation data of one day arc length the results are better than that of using only ground station observations when compared it with precision ephemeris by the above method. Moreover, the average residuals of satellite orbit in tangential, normal and radial residuals are less than 5mm.

system errors; orbit; inter-satellite ranging; combined

2015-03-06。

张博(1986—)，男，硕士研究生，主要从事GNSS数据处理方面的研究。

P

A