发挥数学课堂“ 生成”资源正能量的案例探析

吴 旻

（ 浙江省嘉兴市凤桥镇中心小学）

在课堂之中，教师往往期待与课堂“ 预设”相匹配的学生回答，然而，在真实的课堂之中，却总是“ 生成”教师意想不到的答案。 这些生成需要如何处理呢？是考虑课堂时间让学生马上坐下呢？还是在出现不同的答案的时候给学生几分钟时间， 让学生去讲讲自己是怎么想呢？ 结合案例， 我们思考一下如何合理有效地发挥课堂“ 生成”资源的正能量，进而帮助学生可持续发展。

一、观念上：理解“ 生成”，厘清“ 生成”的重要性

《 义务教育数学课程标准（ 2011 年版）》中指出教学中应当注意“ 预设”与“ 生成”的关系。实施教学方案，把“ 预设”转化为实际的教学活动，在这个过程中，师生双方的互动往往会“ 生成”一些新的教学资源，这就需要教师能够及时把握，因势利导，适时调整预案，使教学活动收到更好的效果。

从学习心理学的角度分析， 学生成长的过程是基于自己原有的生活经验和认知结构，故在课堂上，意外的“ 生成”便是学生已有的认知结构与新内容相碰撞的地方，此时，“ 生成”如果被很好地引导，那么学生将能更好地理解所学内容，故处理好课程的“ 生成”很重要。

从课堂教学的角度分析，意外的“ 生成”既有可能成为课堂上的败笔，又有可能成为课堂上的亮点，其关键在于能否抓住数学本质，让“ 生成”资源更具有教育意义。

二、教学中：识别“ 生成”，加深学生对概念的理解

在课堂教学过程中，“ 生成”蕴藏在学生的动手操作、回答和练习中，细心留意学生的反馈，可以发现很多“ 生成”，顺势而导可以加深学生对于所学概念的理解。

案例一：A 教师执教《 快乐的动物》（ 倍的初步认识）教学时，采用“ 情境引入—动手探知—游戏巩固—故事拓展”的教学流程，清晰地帮助学生建立倍的数学模型，课堂气氛活动，学生整体反应很好，然而当最后一个环节举例应用时，意外发生了。

师：“ 请小朋友自己举例说说谁是谁的几倍。 ”

生1： 小白兔有9 只， 小狗有3 只， 小白兔的数量是小狗的3倍。 师：回答得很好！ 还有哪位小朋友可以举例说明？ 生2：橡皮有11 块，铅笔有3 只，橡皮的数量是铅笔的……（ 学生突然发现不行，迟疑中在思考）师：“ 好！ 你再坐下想想！ ”（ 此时老师有点紧张，不知道怎么处理，赶紧让学生坐下，可是这名学生却好像突然明白怎么回事的，却没机会说了，其他一部分小朋友好像也明白他怎么想的）

案例改进：生2 的回答显然与教师的“ 预设”不一致，但“ 橡皮有11 块，铅笔有3 只，橡皮的数量是铅笔的……”这个“ 生成”是很具有教育意义的，有利于加深学生对于“ 倍的理解”。 学生举出的11 和3 显然不是整数倍的关系，那么可以追问学生：“ 橡皮再加几块就是铅笔的4 倍了。 ”同时借助画一画、圈一圈的方式帮助学生理解，学生很快能想到，橡皮再加1 块就可以了，因为12÷3=4。 这样后面学生再举例的时候就会借助画一画、 圈一圈或除法算式来验证自己举出的数值能否满足整数倍的关系， 促进学生对倍的进一步认识。

三、行为上：读懂“ 生成”，给学生解释的时间和空间

每个看似突兀的“ 生成”，背后都有学生的想法，读取“ 生成”时， 给学生解释的时间和空间， 可以发现学生的创新之处或错误点，对其他学生也有启发之用。

案例二：B 教师执教《 分数的认识》时，通过“ 猜一猜—认一认—做一做—说一说—思维拓展”来引导学生认识分数，在思维拓展时意外发生了。

教师提示学生将答案画在方格纸上，经过学生的不断尝试，产生了图1 中多样化的答案，此时，有一位学生兴奋地举起了小手，激动地展示自己不一样的答案。（ 如图2）。

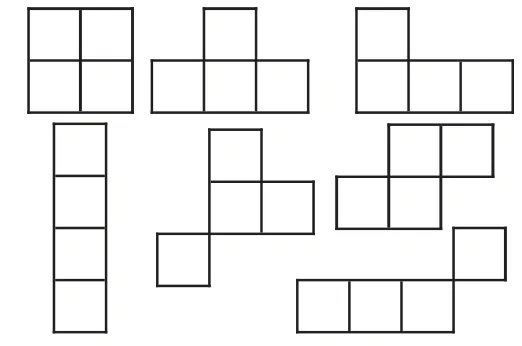
图1

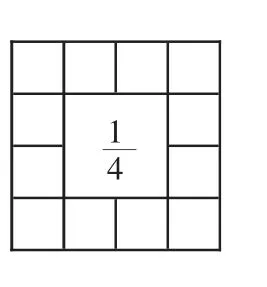
图2

师：她画的是（ 16 份）太多了，同学们都是以方格纸上的一个小正方形为来画的，你这个不对！

生1 失落地充满不解地回到了座位上。

吴正宪.吴正宪与小学数学［ M］.北京师范大学出版社，2006.