基于SEA柔性驱动的动力学模型频域特性研究*

□ 王存堂 □ 任 飞 □ 谢方伟 □ 张 兵

江苏大学机械工程学院 江苏镇江 212013

柔性驱动技术是目前机器人行业亟需解决的一个难题[1]。在康复机器人领域，国内外开发的传统驱动器主要以集成伺服电机的刚性驱动为主，整体柔性不足，在使用过程中极易造成二次伤害。将柔性驱动技术应用于康复机器人领域，可以满足机器人低能耗运动、柔顺化动作、自调整接触等仿人性要求。面对这些问题，MIT的Pratt[2]研发出利用弹簧特性来设计出一种具有仿肌特征的串联弹性驱动器（SEA）。基本SEA结构的特点就是在驱动源和负载之间串联一个弹簧，从而实现精确的力控制，该驱动器具有较低的力输出阻抗、摩擦因数和适当的控制带宽。哈尔滨工程大学的马洪文[3]等人在SEA弹性元件中加入阻尼环节，可以更好地模拟人体肌肉变刚度[4]的特性。

SEA作为一种具有仿生弹性驱动的力输出装置[5]，可以提高康复机器人对人类受损肢体的柔顺性和安全性，克服人机交互过程中的问题。SEA中弹性组件一方面可以抵抗高冲击载荷，实现储存和释放能量；另一方面可通过控制形变量来实现力输出。由于SEA具备上述优点，目前在康复、助力以及工业机器人上的应用日益广泛[5]。近年来，许多研究人员开始关注SEA，在对SEA的动力学模型方面做出了大量分析。但还存在以下两个问题：①忽略电器元件造成的一些因素，动力学模型太简化，对位置源控制方法探讨不足；②针对各种控制方法，在康复机器人方面，SEA的低阻抗特性要求和驱动带宽之间呈反向关系。

由于在SEA中驱动源伺服电机可以对速度、位置精度进行准确控制[5]，同时可以通过闭环反馈将电信号转化成转矩和转速以驱动控制对象。因此按目前控制方式分类，SEA动力学模型可分成两类：位置源或速度源和力源模型[2]，即将电机或液压缸看作理想的位置或速度、以及力输出源，来控制SEA输出端的速度或位移以及输出力。笔者分别建立基于位置源和力源的两种SEA动力学模型，比较其各自在稳定性、快速性和力输出带宽等方面的优缺点。

1 基于位置源控制的SEA动力学模型

基本的SEA模型如图1所示，该模型是在负载和驱动源间串联一组弹性元件[6]。

位置源控制法是指通过内部反馈控制电机的位移输出[7]，来控制输出端的位移、速度、输出力，如图2所示。由图2可知，简化位置源控制法中内部反馈PID控制环节，SEA位置源模型如图3所示。

图3中：fd为给定信号；fl为负载输出力信号；fe为偏差信号；xd为中间位移变量；ke为积分环节的比例增益；T为惯性环节的时间常数；xa为等效质量的位移；vs为相对位移速度；xl为负载位移；ks为弹簧刚度系数；cs为黏滞阻尼系数；ml为负载质量；PID控制参量分别为比例增益kp、积分因子ki、微分因子kd；s为拉普拉斯因子。

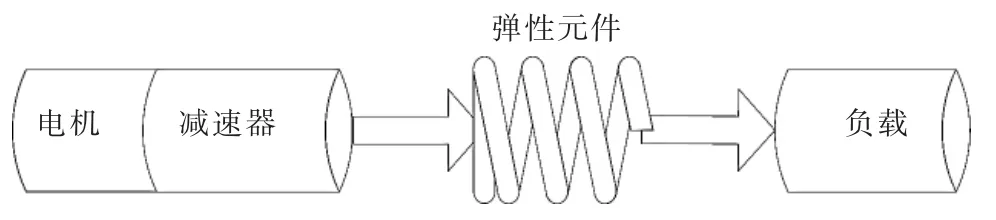
图1 基本SEA 模型

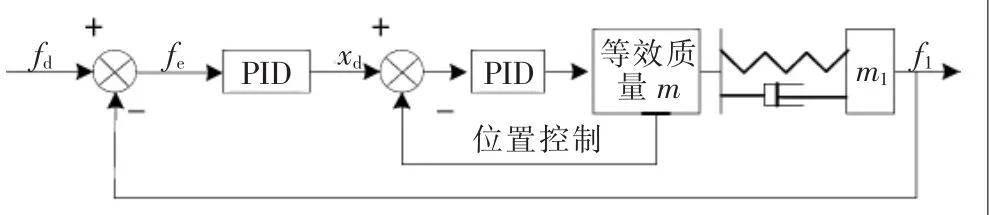
图2 位置源SEA动力学模型

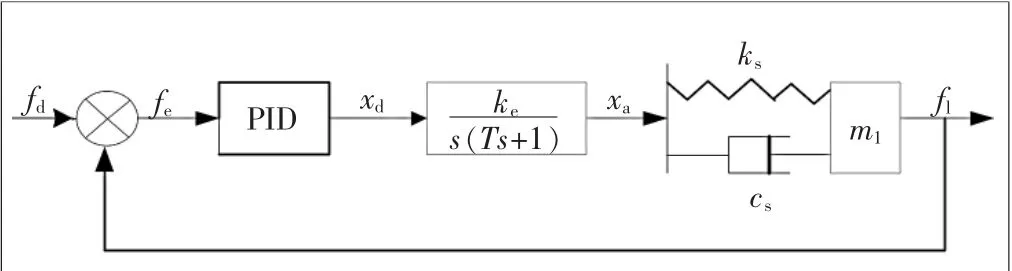
▲图3 SEA位置源动力学简化模型

经 Laplace 变换后，由式（1）、（2）、（3）可得：

为方便分析，不妨先假定驱动器输出端位移为0，即Xl=0。系统开环传递函数为：

分析该系统的闭环传递函数，对于单位负反馈系统有：

经PID控制后驱动位移为：

经Laplace变换后，式（7）变成：

固定负载输出端，即Xl=0，该系统的闭环传递函数为：

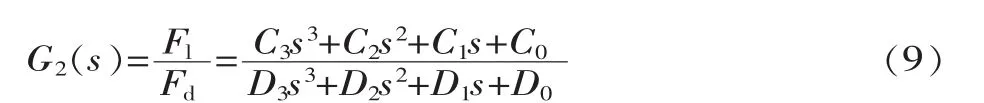
式中：C3=kecskd；D3=kecskd+T；C2=ke（cskp+kskd）；D2=1+ke（cskP+kskd）；C1=ke（cski+kskP）；D1=ke（cski+kskP）；C0=kekski；D0=kekski。

1.1 基于位置源控制的开环频率特性下对闭环系统的分析

1.1.1 不同cs对系统稳定性的作用

设计参数：弹簧刚度ks=2 N/mm，积分环节放大增益ke=0.05，惯性环节时间常数T=2，当阻尼器的阻尼系数 cs分别取 0.01 N·s/mm、0.1 N·s/mm、1 N·s/mm、2 N·s/mm、5 N·s/mm 和 10 N·s/mm 时，分析系统稳定性的变化规律。

根据开环传递函数式（5），分别采用频域分析法中Nyquist判据和Bode判据[8]来分析系统的稳定性。而该系统方程的特征根为：s1=0，s2=-0.5。 该系统在[s]即为横、纵轴平面右半平面内无极点，为最小相位系统。绘制不同cs的Nyquist图和Bode图，如图4和图5所示。

▲图4 开环Nyquist图（位置源、cs）

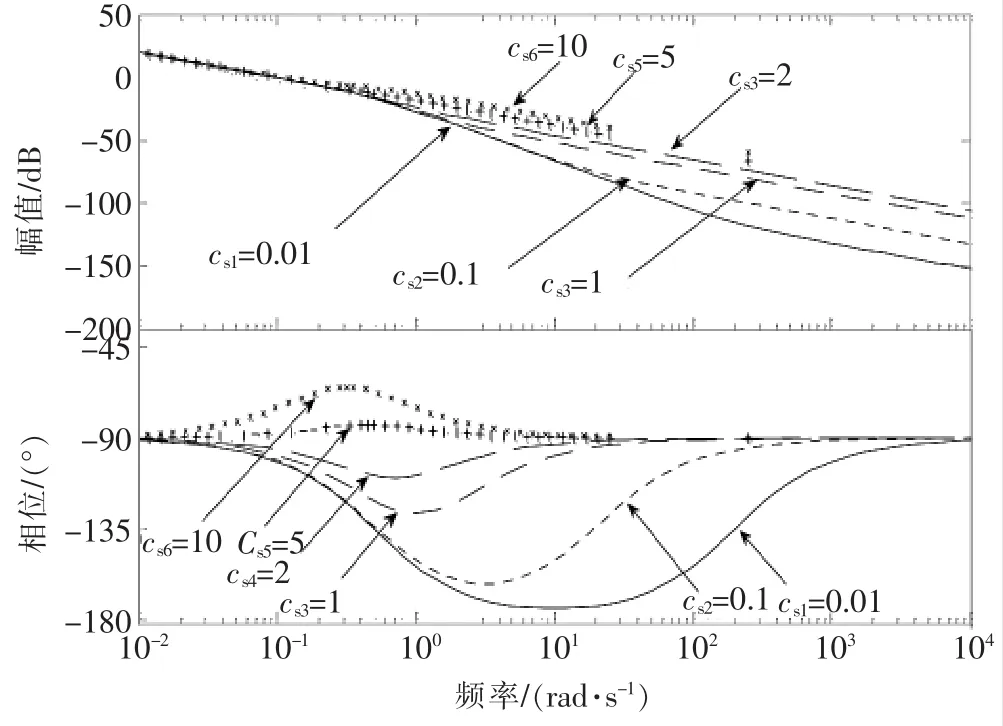
▲图5 开环Bode图（位置源、cs）

由图4可知：①根据Nyquist判据可知，该闭环系统稳定；②该系统奈氏曲线与单位圆相交，均位于虚轴的右侧，幅值裕度均较大。

随着cs增大，各频率特性曲线越来越远离（-1，j0）点。所以稳定性越来越好，且相位裕度在增大。

由图5可知：①由Bode判据可知，该闭环系统是稳定的，与之前分析的奈氏曲线相一致；②在Bode图中，随着cs增大，相角曲线与-180°线无交点且距离越来越远。

该系统在不同cs下幅值裕度均趋于无穷大，相位裕度与cs成正比关系，当cs较大时，系统稳定性更好。

1.1.2 不同ks对系统稳定性的作用

设计参数：cs=0.1 N·s/mm，ke=0.05，T=2，当 ks分别取 0.05 N/mm、0.1 N/mm、1 N/mm、2 N/mm、5 N/mm 和10 N/mm时，分析系统稳定性的变化规律。

根据该系统方程特征根为：s1=0，s2=-0.5。绘制不同ks的Nyquist图和Bode图，如图6和图7所示。

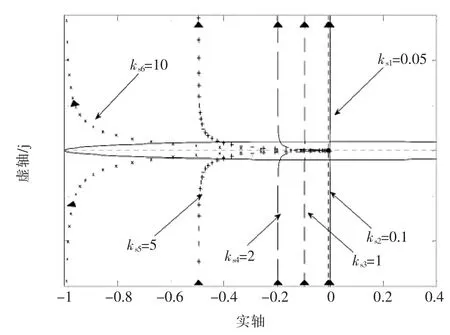
▲图6 开环Nyquist图（位置源、ks）

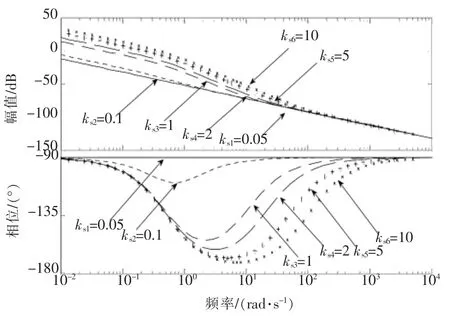
▲图7 开环Bode图（位置源、ks）

由图6可知：①根据Nyquist判据可知，该闭环系统也是稳定的；②该奈氏曲线也都与单位圆相交，均位于虚轴的右侧，系统幅值裕度均较大。

但随着ks增大，各频率特性曲线越来越靠近（-1，j0）点。这说明系统稳定性变差，且相位裕度有减小的趋势。

由图7可知：①根据Bode判据可知，该闭环系统稳定，与图6相一致；②随着ks增大，相位曲线与-180°线无交点且距离越来越近。

因此，该系统在不同ks下幅值裕度均趋于无穷大，而相位裕度与ks成反比关系，即当ks较小时，系统具有更好的稳定裕度。

1.2 基于位置源控制的闭环频率特性指标分析

1.2.1 不同cs对系统稳定性的作用

设计参数：kP=25，ki=2，kd=0，其它变量不变。 当 cs分别取 0.01 N·s/mm、0.1 N·s/mm、1 N·s/mm、2 N·s/mm、5 N·s/mm和10 N·s/mm时，分析系统稳定性的变化规律。当cs不同时，该系统闭环频率特性的谐振峰值Mr、谐振频率 ωr及频宽 ωb见表 1。

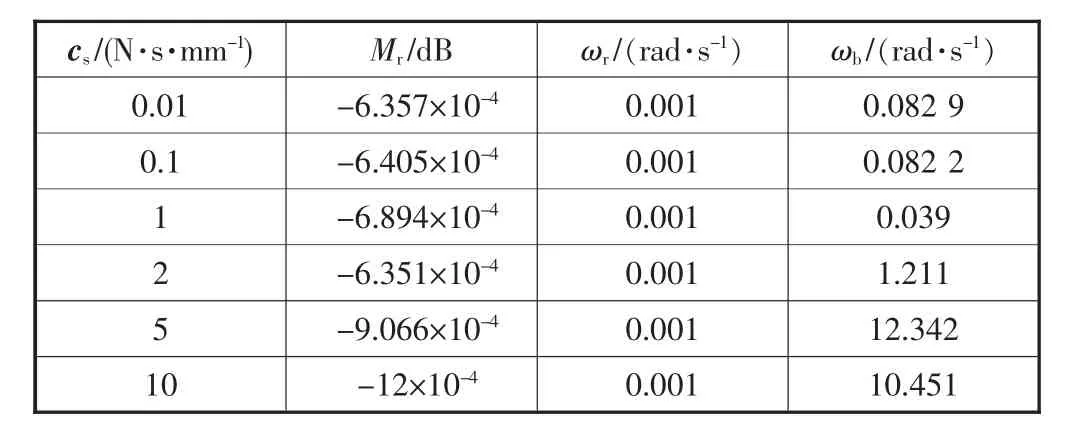
表1 位置源闭环频率特性指标（cs）

由表 1 可知，该闭环系统的 Mr、ωr、ωb随 cs增大的变化规律为：①当该cs较小时，其Mr较小，对应于其时域指标则阶跃响应时基本无超调量，而当cs较大时，Mr均随cs的增大有略微减小的趋势；②随cs的增大，ωr几乎没有变化，而ωb都在不断增大，系统响应速度加快，输出复现精度也越高。

1.2.2 不同ks对系统稳定性的作用

设计参数：kP=25，ki=2，kd=0，其它参量不变。 当 ks分别取 0.05 N/mm、0.1 N/mm、1 N/mm、2 N/mm、5 N/mm和10 N/mm时，分析系统稳定性的变化规律。当ks不同时，该系统闭环频率特性的Mr、ωr及ωb见表2。

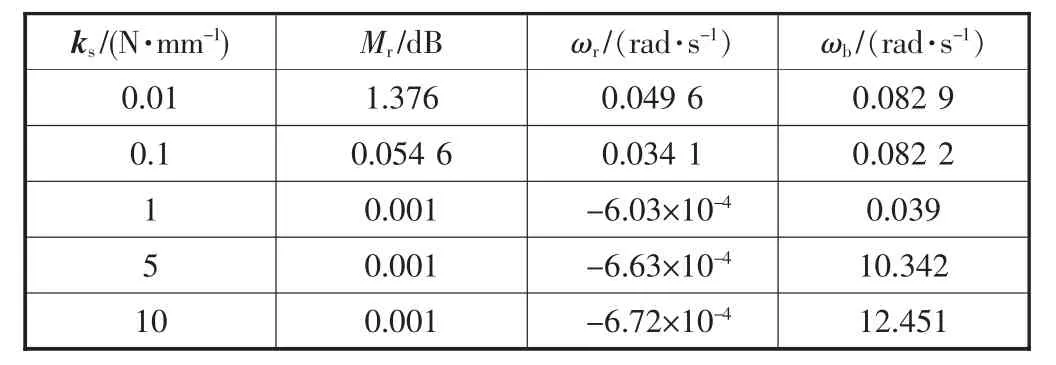
表2 闭环频率特性指标（ks）

由表 2 可知， 该闭环系统的 Mr、ωr、ωb随 ks的变化规律为：①当该系统ks较小时，其对数幅频特性曲线中出现相对较大的Mr；②随着ks的增大，其中ωb具有急剧增大的趋势，瞬态响应速度变快，过渡的上升时间越长，因此采用位置源控制法时应尽量去选择较小的ks。

综上所述，对于位置源控制法（其它变量不变），随着ks增大，系统稳定性下降，而响应速度变慢，输出复现精度变低，高频噪声信号被滤掉。随着cs增大，系统稳定性逐步增大，响应会越明显加快，输出复现精度越来越高。

2 基于力源控制的SEA动力学模型

图8中fa为PID输出力信号，m为传动装置等效质量，ca为电机等效阻尼，ml为负载质量，v为等效质量的速度，vl为负载速度，（其它变量与图3相同）。

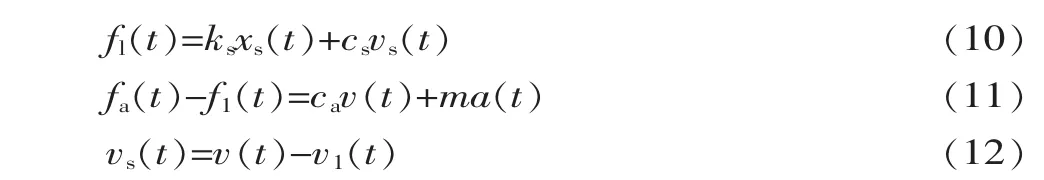
经Laplace变换可得：

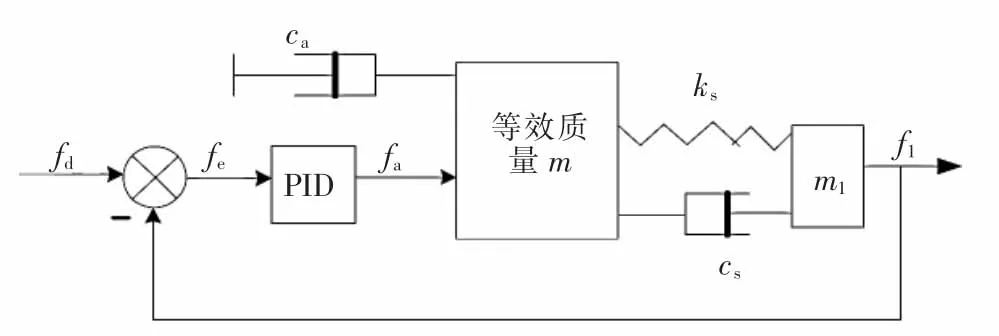
▲图8 SEA力源动力学简化模型

固定输出端负载，即Xl=0，则该系统的开环传递函数为：

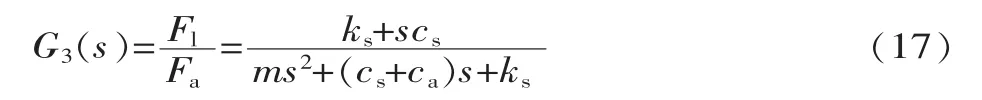
同理基于位置源控制，考虑PID控制，该闭环传递函数为：

式 中 ：E3=kdcs；F3=kdcs+m；E2=kPcs+kdks；F2=cs+ca+kPcs+kdks；E1=kics+kskP；F1=kics+kskP+ks；E0=kiks；F0=kiks。

2.1 基于力源模型的开环频率稳定性下对闭环系统的分析

2.1.1 不同cs对系统稳定性的作用

设计参数：m=1.5 kg，ks=2 N/mm，ca=0.5 N·s/mm。当 cs分别取 0.01 N·s/mm、0.1 N·s/mm、1 N·s/mm、2 N·s/mm、5 N·s/mm 和 10 N·s/mm 时， 分析系统稳定性的变化规律，当该系统取不同cs时，其开环函数的特征根见表3。

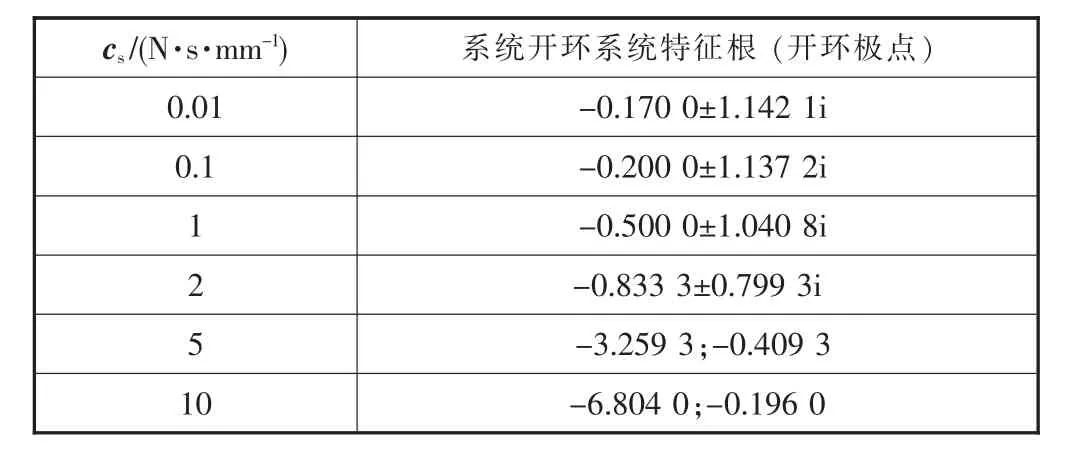
表3 力源开环函数特征根（cs）

因此该系统的开环函数特征根均具有负实部，即在[s]右半平面内无极点存在。

绘制不同cs下该系统开环传递函数的Nyquist图和Bode图，如图9和图10所示。

由图9可知：①根据Nyquist判据可知，该闭环系统稳定；②不同cs的奈氏曲线均与负实轴没有交点，说明幅值裕度均趋于无穷大。

随cs增大，该系统开环奈氏曲线距离实轴上（-1，j0）点越来越远，说明稳定性逐渐增强。

由图10可知：①各对数相频曲线均与-180°线无交点，与在Nyquist图中分析得到的相一致，即幅值裕度较好；②随着cs增大，各相频曲线在低频段均越来越逼近0°线，说明相位裕度越来越好，而在高频段均呈现 -90°的相位滞后现象；③当cs较小时，对数幅频特性图中出现较为明显的Mr，所以cs较小时系统稳定性较差。

2.1.2 不同ks对系统稳定性的作用

设计参数：m=1.5 kg，ca=0.5 N·s/mm，cs=0.1 N·s/mm。 当 ks分别取 0.05 N/mm、0.1 N/mm、1 N/mm、2 N/mm、5 N/mm和10 N/mm时，分析系统稳定性的变化规律，当该系统取不同ks时，其开环特征根见表4。

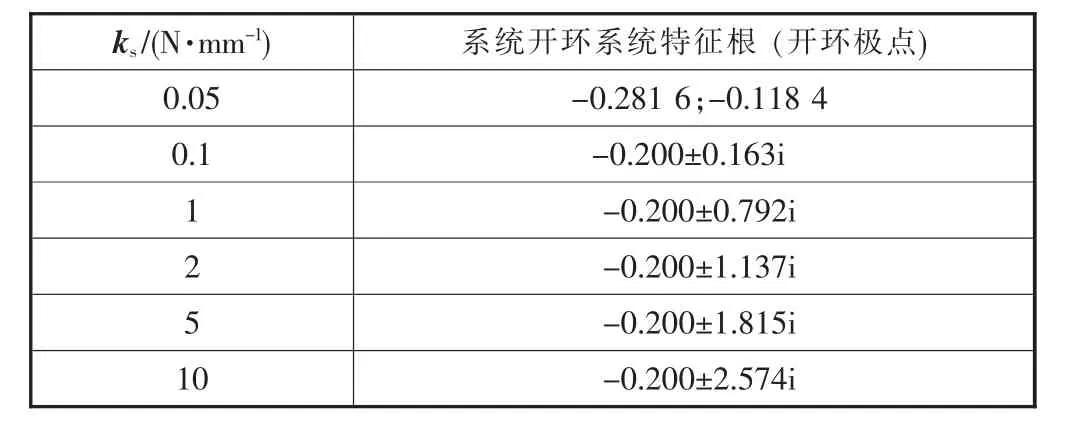
表4 力源开环函数特征根（ks）

▲图9 开环Nyquist图（力源、cs）

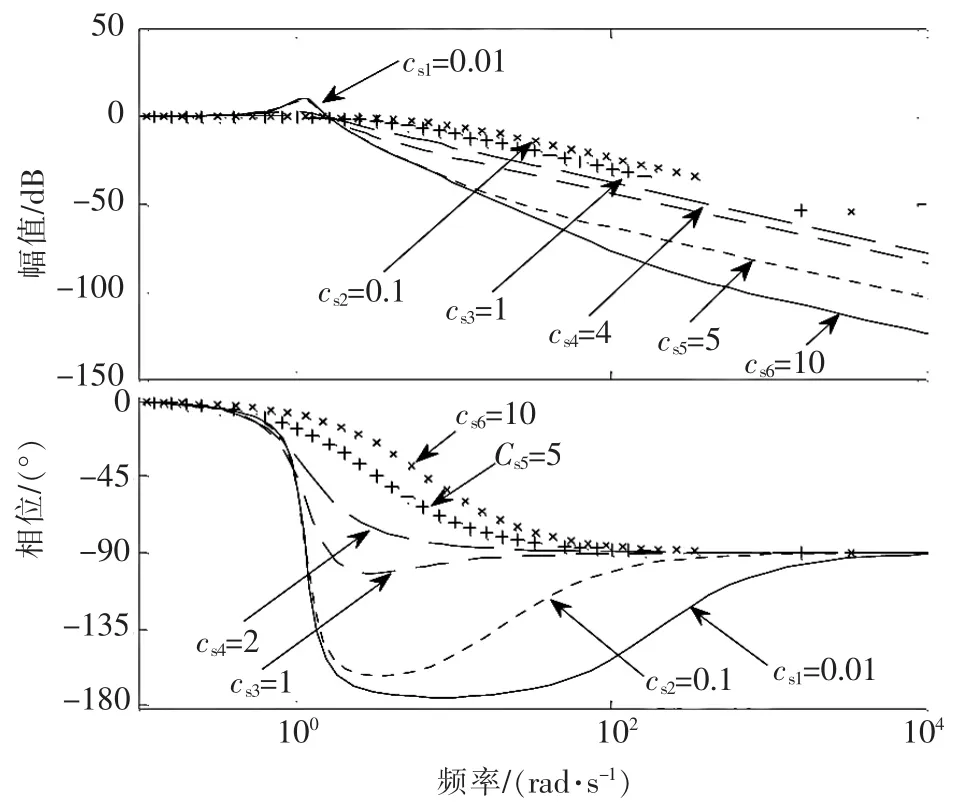
▲图10 开环Bode图（力源、cs）

根据该开环特征根均具有负实部，则在[s]右半平面内无极点。绘制不同ks下系统开环传递函数的Nyquist图和Bode图，如图11和图12所示。

由图11可知：①根据Nyquist判据可知，该闭环系统稳定；②不同ks的奈氏曲线均与负实轴没有交点，这说明幅值裕度均趋于无穷大。

随着ks增大，该系统开环奈氏曲线距离实轴上（-1，j0）点越来越近，说明稳定性逐渐减弱，即ks大时系统稳定性较差。这说明ks和cs对系统稳定性的影响是反向的。

由图12可知：①由于在对数相频特性图中，各曲线均与-180°线没有交点，与在奈氏图中分析得到的相一致，即幅值裕度较好；②随ks增大，各相频特性曲线在低频段均越来越逼近0°线，说明相位裕度好，而在高频段均呈现-90°的相位滞后现象；③当ks较大时，对数幅频特性图中出现较为明显的Mr。

2.2 基于力源控制的闭环频域特性指标分析

2.2.1 不同cs对系统稳定性的作用

设计参数： m=1.5 kg，ks=2 N/mm，ca=0.5 N·s/mm，kP=25，ki=2，kd=0。 当 cs分别取 0.01 N·s/mm、0.1 N·s/mm、1 N·s/mm、2 N·s/mm、5 N·s/mm 和 10 N·s/mm 时，分析系统稳定性的变化规律。当cs不同时，该系统闭环频率特性的 Mr、ωr及 ωb见表 5。

▲图11 开环Nyquist图（力源、ks）

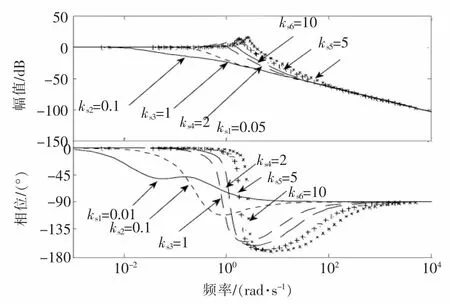
▲图12 开环Bode图（力源、ks）

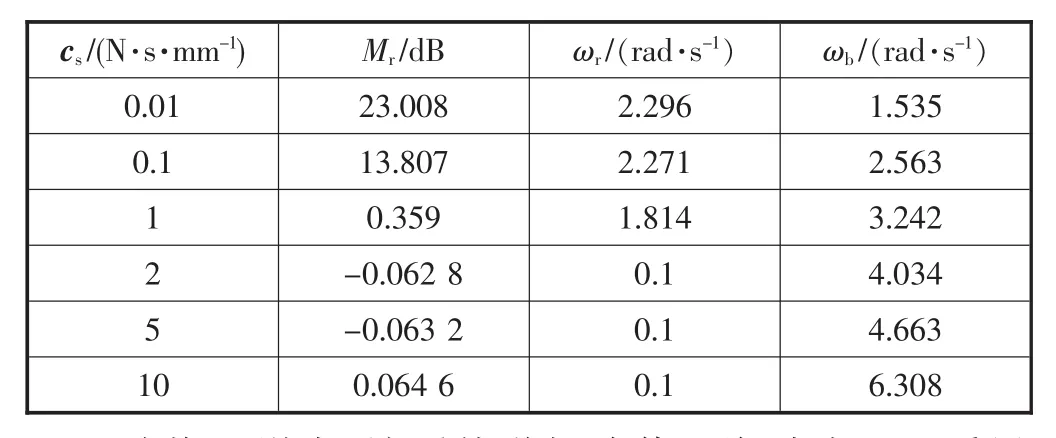
表5 力源闭环频率特性指标（cs）

随着cs增大，该系统谐振峰值逐渐减小至几乎没有，说明稳定性逐渐增强。同时，频宽也越来越大，表明：系统的响应速度加快，高频信号也能保证较低的失真度，而谐振频率逐渐减小说明系统的瞬态响应速度变慢。

2.2.2 不同ks对系统稳定性的作用

设计参数： m=1.5 kg，cs=0.1 N·s/mm，ca=0.5 N·s/mm，kP=25， ki=2， kd=0。 当 ks分别取 0.05 N/mm、0.1 N/mm、1 N/mm、2 N/mm、5 N/mm 和 10 N/mm 时， 分析系统稳定性的变化规律。当ks不同时，该系统闭环频率特性的 Mr、ωr及 ωb见表 6。

表6 力源闭环频率特性指标（ks）

随着ks增大，该系统的Mr逐渐增大，说明稳定性逐渐减弱。同时，ωr和ωb也越来越大，表明：系统瞬态响应速度加快，高频信号也能保证较低的失真度。据上分析，对于力源模型而言，通过增加ks，系统稳定性减弱；但是响应速度和瞬态速度均加快，高频信号也能保证较低的失真度。

3 结论

基于SEA柔性驱动的动力学模型稳定性分析，对机器人的柔顺控制具有一定的实践指导意义。通过对比分析两种模型，得到结论如下。

（1）稳定性方面，力源＞位置源。

（2）ks和cs不仅会显著影响系统稳定性而且会影响其力输出带宽、幅相频率特性，同时为保证SEA的柔性，选择合适参数是非常重要的。

（3）与位置源控制法相比，力源控制法具有较大的力输出带宽。

（4）与力源控制法相比，位置源的幅值相位特性表现也不是很理想，主要原因是由于位置源模型是通过内部反馈来控制电机位移的，容易忽略等效质量对稳定性的影响，其固有模型误差较大。

总之，在合理条件下，SEA的控制方式应优先选择力源控制法。

[1]盖玉先，刘伟颖.助行腿膝关节的串联弹性驱动器系统设计[J].机械设计与制造，2014（9）：33-36.

[2]Pratt G A.Series Elastic Actuators [C].IEEE/RZJ International Conference on Intelligent Robot and System.USA，Pittsburgh，1995.

[3]赵朋.串联弹性驱动器动力学模型及其特性分析[D].哈尔滨：哈尔滨工程大学，2012.

[4]马挺，郭险峰.外骨骼机器人柔性变刚度驱动器设计[J].科技资讯，2014（35）：65-69.

[5]何福本，梁延德，孙捷夫，等.基于SEA的机器人仿肌弹性驱动关节研究[J].中国机械工程，2014（7）：900-905.

[6]Lens T，von Styko O.Safety Properties and Collision Behavior of Robotic Arms with Elastic Tendon Actuation[C].7th German Conference on Robotics （ROBOTIK），Munich，2012

[7]殷跃红，尉忠信，朱剑英.机器人柔顺控制研究[J].机器人，1998，20（3）：73-81.

[8]彭瑞珍，董海棠.控制工程基础[M]，北京：高等教育出版社，2010.

（编辑 平 平）

不断创新，保持领先——山高刀具2015-2秋季新品闪亮发布

今年秋季，山高扩展了多个广受欢迎的产品系列，包括Combimaster、Jabro-Solid2、Minimaster Plus 新 小 魔 王 、Steadyline 刀 头 、Threadmaster 丝 锥 和Precimaster Plus。

山高还推出了3种TP材质等级（TP2501、TP1501和 TP0501），可满足该应用领域中的各种需求。由于这些材质等级首次采用了山高新一代Duratomic金刚甲镀层技术，因此它们是最可靠、最可预测和最高效的产品。80多年来，山高不断提供车间所需的刀具、工艺和服务，以保持领先制造曲线。

适用于Steadyline抗振刀柄的带有GL连接的MDT刀头

山高目前将其最新开发的 GL连接与新型多方向车削 （MDT）可互换刀头相整合，用于其Steadyline模块化减振刀杆系统。GL连接和Steadyline刀杆的结合，使用新型MDT刀头进行割槽和车削时，可获得出色的精度和表面粗糙度。

凭借极其精准的 GL连接，用户可以快速、轻松、准确地在 Steadyline刀杆上更换MDT刀头和其它类型的刀头。在刀杆设定到位后，无需重置系统，即可安装和重新安装刀头。获得专利的 GL连接的多面锥形接触面有两个安装位置，因此MDT刀片的切削刃可以面朝上或面朝下定位，实现有效的切屑控制。

Combimaster M20

这一全新的更大刀柄连接采用 M20螺纹，使Combimaster拥有更大直径的刀具。它提供了出色的稳定性和强度，有助于实现更高的材料切除率。M20螺纹可确保刀杆和刀体之间的连接具有最大强度。在大多数情况下，Combimaster M20可让用户将金属切除率和切削深度提高达15%，从而提升总体加工性能。对于Combimaster产品系列，山高对M20连接进行了调整，使其适用于30多种新刀柄类型及50多种铣刀类型，包括圆刀片和高进给刀片产品系列。其他产品领域还包括新连接，例如方肩、插铣、球头和铝加工铣刀系列。

JABRO·-SOLID2立铣刀JS554-2C

作为 Jabro JS554整体硬质合金立铣刀系列的最新成员，JS554-2C具有能够在高级粗加工应用中显著提高进给量和金属切除率的新功能。在铣削加工过程中，这一新刀具能够以优化的接触弧或啮合角度运行，使用户能够充分利用现代机床的反应速度和积极的 CAM软件刀具路径策略。JS554-2C的高级粗加工还最大限度地延长了刀具寿命，提高了零件的表面粗糙度质量，JS554-2C可以使用刀具的整个切削长度（ap）执行侧铣粗加工走刀，分屑槽形成大小可控的切屑，并防止任何长切屑重切过程（重切会使粗加工立铣刀迅速变钝或受损）。该刀具能够采用高径向啮合，有助于减少所需的粗加工走刀次数，缩短整个零件加工周期。此外，更短的切屑还可防止堵塞机床的切屑输送系统，从而可以确保无人化加工的顺利进行。

山高将JS554-2C归类为适用于所有材料的高端通用铣刀，可替代通常用于获得相应高级粗加工结果的"材料特定"刀具。该刀具几乎能在所有 CAM模块中进行加工，因此具有通用性并且易于使用。

Minimaster·Plus新小魔王

山高为其业界领先的 Minimaster Plus新小魔王可更换刀头刀具系统推出了全新的四刃刀头，这一四刃刀头以及现有的三刃刀头均可应对更大的切削力，从而在粗加工和半精加工中提高金属切除率。四刃刀头具有更大的螺旋角，采用了现有 Minimaster Plus新小魔王刀头的相同设计特性和优点，并且新增了0.7xD短刃长的产品，可大幅提升其稳定性。稳定性的增加，使这款产品能更好地适应苛刻的工况，以及更适应在5轴加工中更多的底刃加工。更高的稳定性让这款短刃长产品特别适合进行大余量材料切削，短刃长刀具在径向切削力大于轴向切削力时，更有优势，而较长刃长产品正好相反。

Threadmaster·丝锥

山高继续扩展其 Threadmaster丝锥系列，新增了材料专用的丝锥以及更大螺纹尺寸的型号。目前，山高在其现有的通用丝锥产品系列中提供了330种特殊ISO材料专用丝锥以及 200多种新规格/尺寸，它们具有通用性，其中很多新丝锥都配有内冷功能。

山高的全新直槽、螺旋槽、螺旋尖和挤压型丝锥专为 ISO P、M、N和 K材料而设计，可提供最佳的性能和有效的排屑控制。直槽丝锥的尺寸范围为 M4到M42，带有或不带内冷通道；螺旋槽丝锥的尺寸范围为 M1到M30；用于 ISO P的螺旋尖丝锥的尺寸范围为M1到M30；挤压丝锥的尺寸范围为M1到M48。

M4和M5的丝锥尺寸是具有内冷功能的最小尺寸，山高的所有丝锥（专用和通用）均采用专门设计的镀层，可以提高性能并延长刀具寿命。

新一代Precimaster·Plus铰刀

山高推出的两种全新刀杆设计可提供浮动和可调性，从而实现充分优化的高精度铰削加工。作为Precimaster Plus转位刀头铰削系统的接长杆，全新的PMX-FL和PMX-AD刀杆大大改善了孔表面粗糙度，消除了跳动量并纠正了偏差，并且无需使用专用刀柄。山高全新的刀杆采用了适用于此类功能的紧凑内部系统，因而无需使用专用刀柄即可提供浮动和可调性功能。相比专用刀柄，新刀杆还可使铰刀更靠近机床主轴头，从而减少刀具悬伸量。

山高的内置浮动系统采用纯机械式，适用于静态和车床铰削应用，比其它类似刀具上使用的常见橡胶或合成橡胶技术更为稳定。此外，用于旋转应用的山高新刀杆上的内部调整系统在设计上采用了机械式，并借助6个螺钉来提供精准的设置，并将主轴偏差量有效地纠正到0.005 mm以下。

TP2501、TP1501和 TP0501钢件车削材质等级

TP2501、TP1501和TP0501刀片为ISO P钢件材料类别中的工件提供大量解决方案选择，同时还适用于不锈钢和铸铁。已用切削刃检测功能是对客户反馈的直接回应，因为操作员在尝试识别已用切削刃时通常会感到很困难。这些材质等级能使用户快速找出与工件接触过的切削刃，甚至是在非常轻的精加工走刀中。