基于ARMA模型的上证指数月度数据实证分析
丛 正,袁基瑜
(1.东北财经大学 金融学院,辽宁 大连 116025;2.黑龙江工程学院 经济管理学院,黑龙江 哈尔滨 150050)
基于ARMA模型的上证指数月度数据实证分析
丛 正1,袁基瑜2
(1.东北财经大学 金融学院,辽宁 大连 116025;2.黑龙江工程学院 经济管理学院,黑龙江 哈尔滨 150050)
上证指数是由上海证券交易所编制,反映上海证券交易市场的总体走势,为投资者提供新的投资尺标。根据美国统计学家Box Gep和英国统计学家Jenkins G M提出的Box-Jenkins方法,即时间序列分析法,以2009年1月至2013年2月上证指数的月收盘价格为研究样本,由不平稳的原始数据经过变换形成新的平稳时间序列,建立ARMA模型进行定量分析,得出相邻6个月收盘价之间的关系模型。
上证指数;月度数据;ARMA模型
上证综指即上海证券综合指数(Shanghai composite index),简称上证综指,它是上海证券交易所编制的,以上海证券交易所挂牌上市的全部股票为计算范围,以发行量为权数综合,反映了上海证券交易市场的总体走势。上证所将选择已完成股权分置改革的沪市上市公司组成样本,发布新上证综指,以反映这批股票的市场走势,为投资者提供新的投资尺标。
新上证综指发布以2005-12-30为基日,以当日所有样本股票的市价总值为基期,基点为1 000点。新上证综指简称“新综指”,指数代码为000017。新综指当前由沪市所有G股组成。此后,实施股权分置改革的股票在方案实施后的第二个交易日纳入指数,指数以总股本加权计算。据统计,以2005-12-15收盘价计算,新综指市价总值为3 927亿元,流通市值为1 425亿元,占市场的比重分别为18%及22%。随着股权分置改革的不断深入,新综指占市场比重将逐渐增大。2005-12-15新综指市盈率为12.14倍,比上证综指低23.47%。新上证综指是中国证券市场由权威机构发布的反映股权分置改革实施后公司概况的指数,随着股权分置改革的全面推进,将不断有新的样本加入新上证综指。
1 ARMA基本原理及建模步骤
1.1 ARMA模型的基本原理
ARMA模型(Auto-Regressive and Moving Average Model)是研究时间序列的重要方法,由自回归模型(AR型)与滑动平均模型(MA型)混合构成。由美国统计学家BOX GEP和英国统计学家Jenkins G M在20世纪70年代提出的时间序列分析模型。建立ARMA模型的前提条件是,建立模型的时间序列是由零均值平稳随机过程产生的,其过程的随机性质不变,表现为序列的均值、方差不随时间T变化,在图形上表示为所有样本点都在某一水平线上下随机地波动。一般的ARMA(p,q)模型可表示为
时间序列yt服从(p,q)阶自回归移动平均模型,或者记为
式中:εt为白噪声序列,p和q都是非负整数。q=0,模型即为AR(P);p=0,模型即为MA(q)。ARMA模型是AR(P)模型和MA(q)模型的结合,其主要研究变量当期值与若干滞后期值及误差项之间的关系,并在此基础上对后期数据进行预测,是时间序列分析中经常要用到的模型。下面就以上证指数为例进行实证分析。ARMA分析对象是随机特性不变的平稳序列,对于非平稳的时间序列数据,不能直接用ARMA模型处理,只有转换为平稳序列,才可以用ARMA(p,q)。
1.2 时间序列的分析工具和方法
1)ARMA的定阶方法。对新生成的平稳时间序列进行相关系数检验,观察自相关系数AC图和偏自相关系数PAC图,看有多少个自相关系数(偏自相关系数)落在5%的置信区间之外,其余的落在区间之内,表明该平稳序列的移动平均过程阶数(自回归过程的阶数)就为多少。若AC和PAC都没有明显的截尾性,则试试ARMA模型,通过反复的尝试,有可能存在不止一组的(p,q)值都能通过识别检验,这时比较它们的AIC值,选择AIC值越小的那个模型。
2)ADF检验方法。ADF检验也称为单位根检验,即检验时间序列是否存在单位根。一般进行ADF检验的步骤如下:①对原始时间序列进行检验,此时第二项选level。如果ADF检验值(t值)大于某显著水平值(一般是5%),则不通过检验,即存在单位根,说明原始时间序列不平稳;②对原始时间序列进行一阶差分后再检验,即第二项选1st difference,若仍然未通过检验,则需要进行二次差分变换;③二次差分序列的检验,即第二项选择2nd difference,如果ADF检验值(t值)小于某显著水平值(一般是5%),则通过检验,即不存在单位根,一般到此时间序列就平稳了。
1.3 建模步骤
ARMA模型要求时间序列必须平稳,在确定的时间内数据受到的影响必须大致相同。若所给序列是非平稳的,BOXJIN提出了具有广泛影响的建模思路,可分为以下几步:
1)对原序列数据平稳性检验,如果为非平稳序列,可以通过差分法或对数变换使序列满足平稳条件。
2)求出观察时间序列的样本自相关系数AC和样本偏自相关系数PAC等统计量,根据AIC(赤池准则)和SC(施瓦茨准则)确定ARMA模型的阶数p和q。
3)利用最小二乘法进行参数估计,并进行参数显著性检验,检验模型本身的合理性。
4)检验模型的有效性,即残差的白噪音检验,如果拟合模型没有通过检验,转向步骤2),重新选择模型再拟合;如果通过检验,可以确定模型。
5)利用拟合模型,选择预测数据序列的未来走势。
2 对上证指数月收盘价的实证分析和预测
基于以上的建模步骤和理论介绍,选取实证研究数据。由于2008年上市公司数量的增加,上证指数收盘明显变化,选取2009年1月至2013年12月的月上证指数收盘价格为研究样本,对各月收盘时上证指数的变化进行分析。
2.1 平稳化处理
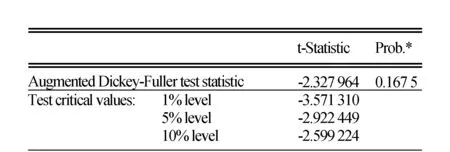
图1 上证指数原始序列的单位根检验
由图1的单位根检验可知,上证指数月收盘价原始序列Y的ADF检验t统计量检验值为-2.328,均大于1%、5%、10%置信水平下的t检验值,且其Prob.值为0.167 5,远远大于0.05,序列Y显著接受存在一个单位根的假设,所以原始序列不平稳,需要对原始序列进行二次差分,使其平稳化。先对Y一阶差分得:di=yi+1-yi,再一阶差分得:zi=di+1-di=yi+2-2yi+1+yi。于是由不平稳序列Y经过变换得到了平稳的序列Z。
2.2 序列的自相关系数和偏自相关系数
从图2可看出,序列Z在0.05的显著性水平下显著拒绝存在单位根的原假设,所以认为Z是平稳的,可以对其建立ARMA模型。由图3可知,平稳时间序列Z的自相关系数呈现出拖尾特征,逐渐减小,偏自相关系数的前面三阶不在5%的置信区间内,所以平稳时间序列Z为AR(3)模型。

图2 Z的单位根检验

图3 平稳时间序列Z的相关分析
由图4的回归结果可知序列Z的AR(3)模型为
(1)
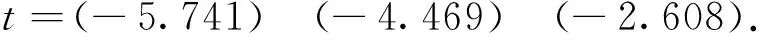

图4 Z的AR(3)模型的估计结果

图5 AR(3)模型的残差相关

图6 AR(3)模型的拟合
2.3 残差检验
通过图5可知,回归方程的残差序列基本上是一个0均值的平稳序列,从图5的回归方程残差序列的相关系数可以看出不存在序列相关,且模型的各项统计量也很好。从图6的拟合也可以看出,模型拟合效果非常好。
将zi=di+1-di=yi+2-2yi+1+yi代入式(1),有
yt=1.177yt-1-0.062yt-2+0.215yt-3+
0.048yt-4-0.378yt-5+εt.
同时还预测出2014年1月、2月、3月和2013年12月份的上证指数收盘价情况,见表1。

表1 2013年12月和2014年1月~3月
3结束语
本文利用Box-Jenkins思想,对上证指数的月度收盘价这一时间序列进行建模和分析,了解了金融市场指数变化的基本特点。
通过对上证指数的时间序列分析,以2009年1月至2013年12月的月上证指数收盘价为研究数据样本,对各月收盘时上证指数的变化进行实证分析,得出相邻几个月收盘价之间的关系模型:yt=1.177yt-1-0.062yt-2+0.215yt-3+0.048yt-4-0.378yt-5+εt。
ARMA模型很好地处理了非平稳时间序列的建模问题,在时间序列预测上表现良好。借助EVIEWS 6.0软件,将模型用于股票指数等时间序列的研究和预测,为趋势预测和指导提供帮助和支撑。当然,因为指数变化的复杂性,模拟和预测还需要进一步的研究。
[1] 冯盼,曹显兵.基于ARMA模型的股价分析与预测的实证研究[J].数学的实践和认识,2011,(40)22:85-89.
[2] 徐静.ARMA模型及其应用[J].立信会计高等专科学院学报,2001,(15)3:21-23.
[3] 孙敬水.中级计量经济学[M].上海:上海财经大学出版社,2008.
[4] 高铁梅.计量经济分析方法与建模[M].北京:清华大学出版社,2005.
[5] 丛正,许佳萍.基于ARMA模型的辽宁省农村金融缺口测算研究[J].山东农业大学学报,2013(4).
[6] 丛正.农贷、房价与家庭人均收入——基于辽宁1980-2011数据的实证分析[J].山东农业大学学报,2014(3).
[7] 何晓光,朱永军.中国A股市场收益波动的非对称性研究[J].数理统计与管理,2007(1).
[8] 王鹏,吕永健.基于消息模型的股票市场波动与相关消息因素的关系研究[J].数理统计与管理,2013(6).
[9] 郭璐,韩立岩,李东辉.交叉上市的信息传递及整合性:股改前后的变化——来自沪市A、B股的证据[J].管理世界,2009(1).
[责任编辑:郝丽英]
Empirical analysis of monthly data of the Shanghai composite index based on ARMA mdel
CONG Zheng1,YUAN Ji-yu2
(1.College of Finance; Dongbei University of Finance and Economics, Dalian 116025,China; 2. College of Economics and Management, Heilongjiang Institute of Technology, Harbin 150050,China)
The Shanghai index is compiled by the Shanghai Stock Exchange,reflecting the overall trend of stock market in Shanghai,providing investors with a new investment scale.According to the American statistician Box Gep and British statistician Jenkins G M,who put up with the BOX-Jenkins method that is the time series analysis method,combining the Shanghai composite index of month closing price as the research sample from January 2009 to February 2013,not smooth of raw data through transformation to form new stationary time series,and set up ARMA model to quantitative analysis.Finally it obtains the adjacent relationship model between the closing price of 6 months.
Shanghai index;monthly data;ARMA model
2014-10-26
沈阳市科技局软科学研究专项(F14-230-5-16)
丛 正(1973-),男,博士研究生,研究方向:资本市场.
F8
A
1671-4679(2015)02-0052-03

