基于Matlab的差分GPS算法分析与软件测试
黄 金,石杏喜
(1.中铁工程设计院有限公司,江苏 南通 226000;2.南京理工大学 理学院,江苏 南京 210094)
基于Matlab的差分GPS算法分析与软件测试
黄 金1,石杏喜2
(1.中铁工程设计院有限公司,江苏 南通 226000;2.南京理工大学 理学院,江苏 南京 210094)
对GPS定位中观测的卫星数据进行正确的分析处理是差分GPS定位工作的前提。主要论述差分GPS算法及其观测模型、基于Matlab程序的载波相位差分算法的数据处理方法,并得出最后的仿真结果。结果表明该数据处理方法是正确且有效的。
差分GPS;工程测绘;观测模型;数据处理;Matlab程序
国内外对于差分GPS定位技术的研究甚多,虽然各种研究方法大相径庭,但主要都是为了能够得到实时而准确的定位信息,研究中最重要的就是对观测数据的分析处理,来得到相应的改正数,数据处理精确与否将直接影响差分定位精度[1]。本文主要对差分GPS算法进行了分析,并采用Matlab程序语言进行数据处理和软件测试,以图形的方式直观地表达载波相位差分计算过程,并进行相应的分析。
单基站差分GPS是在一个已知三维坐标的点设置一个基站,并通过它连续接收GPS卫星发射的信号,根据相应的数据传输处理得到移动站的定位结果[2]。差分GPS原理如图1所示。
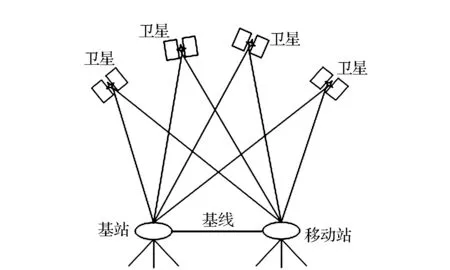
图1 差分GPS原理
根据研究事实证明,差分GPS已将卫星钟的误差和卫星星历误差削弱,还可以将电离层和对流层的延迟误差消除,使得定位精度得到很大程度的提高。所以,差分GPS定位技术在最近几年得到了快速发展和广泛应用[3]。按照差分GPS基准站发送的信息方式以及算法的精度,差分GPS的分类及其发展过程如图2所示。
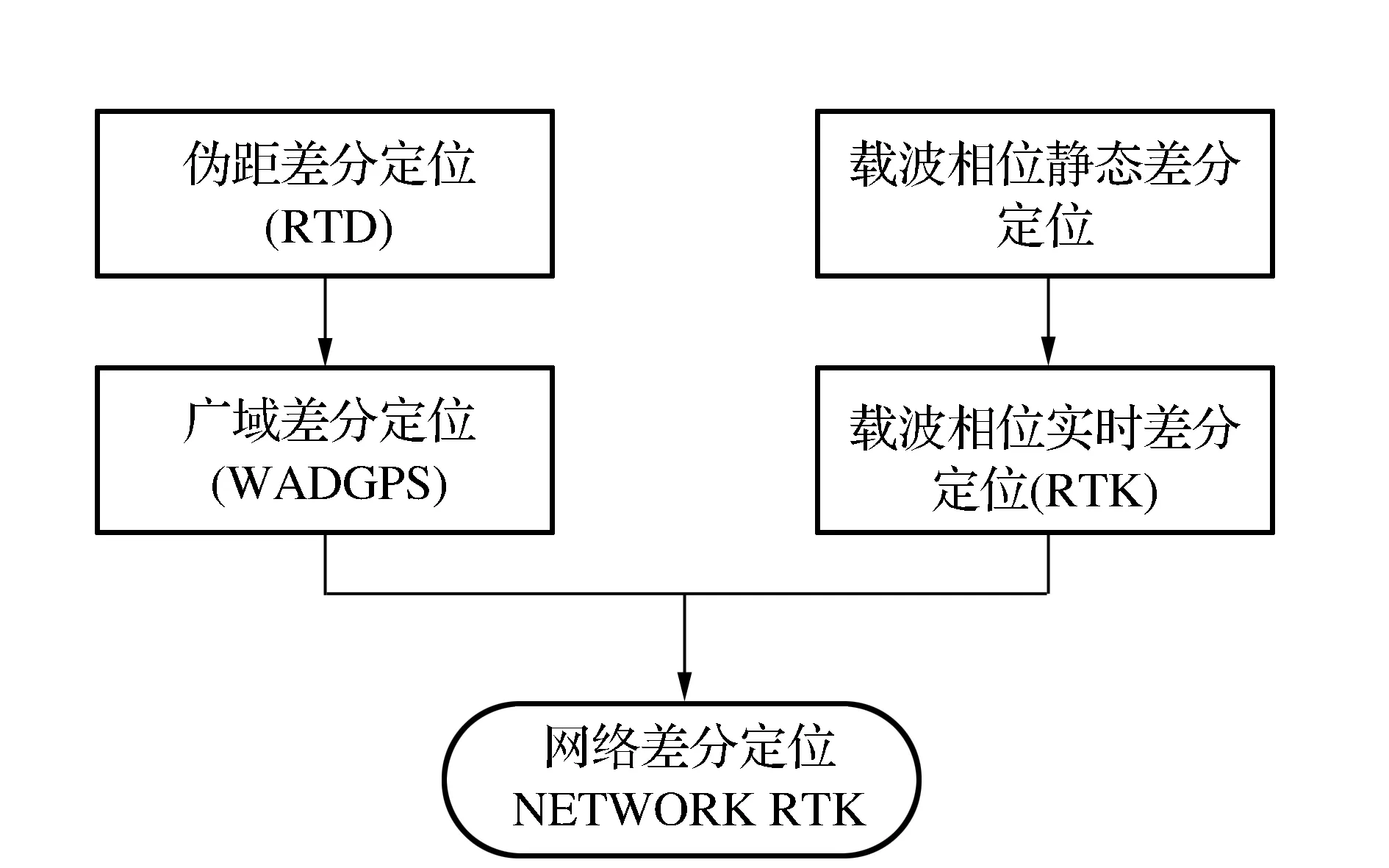
图2 差分GPS分类及发展历程
上述各类差分GPS的工作原理是一样的,都是经由基站发送改正数,用户接收后再根据改正数对定位信息进行修正。不同的就是发送的改正数不一样,导致最后修正的结果不一样。
在GPS差分定位中,其中一项非常重要的观测数据是卫星到地面点之间的距离,此距离的观测精度对定位精度起着非常重要的作用。由于C/A码的波长大,载波相位波长小,采用周数乘以波长就是卫星到地面点间的距离,如果误差为一周的话,那么C/A码的卫星到地面点间的距离误差要比载波相位大很多,由于P码被加密,无法作为民用,所以本文以差分算法中精度最高的载波相位实时差分定位(RTK)作为研究对象[4]。
1 载波相位差分GPS算法分析
在进行载波相位差分GPS基线向量解算之前,首先必须要得到GPS卫星的星历文件和观测文件,这些数据文件是通过一段时间的连续观测而得到的。为了能够得到良好的定位结果,对基站GPS天线的放置位置有严格的要求,一般放置在空旷场地或楼层顶端以减少周围环境对信号的影响。
在进行载波相位实时差分定位时,通常为了能够尽可能地消除或减弱相关误差的影响以及保留尽可能多的有效信息,会对载波相位差分的观测模型进行一些处理,将其组成线性相关的观测方程,并且作单差以及双差处理,其中单差双差是载波相位观测量的基本线性组合形式。
1)原始的GPS载波相位观测方程
(1)
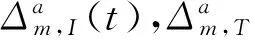
2)载波相位单差观测模型
(2)
式中:Δ为两个站之间相应项的差值,ΔΔ为两个站之间卫星的延迟之差。
3)载波相位双差观测模型
(3)
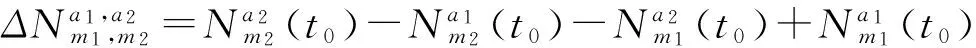
在得到了载波相位单差双差方程后,就可以进行基线向量的解算[5]。如果基站m1的WGS-84坐标(xm1,ym1,zm1)已知,当要求基站m2的WGS-84坐标(xm2,ym2,zm2)时,采用单基线解算模型,取两个基站所含有的线性独立的双差观测方程进行计算,通过平差计算即可求解出两个基站之间的基线向量,但是必须同时观测至少4颗卫星才可以得到基站m2的三维坐标[6]。
2 基于Matlab的数据处理
数据处理软件Matlab具有优秀的数值处理计算能力和卓越的数据可视化功能。因此,在数据处理方面Matlab的优势显而易见,很多研究领域都采用Matlab来对实验所得的数据进行相应的处理。Matlab具有强大的矩阵运算功能,并且提供了强大的图像数据可视化的功能,它既可以绘制二维图像也可以绘制三维图像[7]。
在本文的载波相位差分GPS算法中,涉及的观测数据处理都离不开矩阵运算组合,为了能够快速并且准确地处理数据得到最后的基线解算结果,就需要使用Matlab对数据进行处理分析。图3所示为GPS数据处理的简单过程。
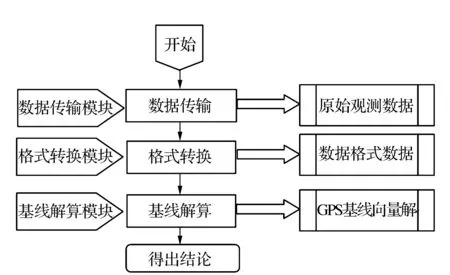
图3 载波相位差分处理流程
2.1 数据文件的读取与处理
2.1.1 星历文件的读取
该程序通过GPS接收机接收到的卫星广播星历数据是以后缀名为.01N的格式保存,可以直接用TXT打开方式查看数据。下面采用Matlab对星历文件进行读取工作并作相应的数据处理。
星历文件的读取程序为readNav.m。打开cpy D0012361.01N文件,并赋值于fid,定义两个空数
组,分别为NavData(存储星历数据)和OneNav(存储一条星历数据)。然后开始对该文件进行读取工作,读取一行。
从每一颗卫星的卫星号开始读取并且跳过表头。对数据依次读取,当读取的数据size(OneNav,1)>37时,即进入第二颗卫星的星历数据,将读取的数据存储在OneNav中,作为NavData的一列。按此循环,依次对各颗卫星的星历数据进行读取,并组合到NavData中,形成一个38行N列的数组。每颗卫星的最后三个数据无意义,为了避免数据冗余,采用D001NAV = NavData(1:end-3,:)去除最后三行数据,最后将D001NAV保存。
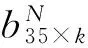
式中:nik为卫星编号,tk,j为第k组卫星的星历时间,ak,j为第k组卫星的参数数据,分别对应于各卫星坐标计算参数。
这样就完成了对星历文件的读取工作,并且将最后得到的数组保存,便于进行数据处理、将数据进行时钟同步等。
2.1.2 观测文件的读取
本程序通过GPS接收机接收到的卫星相位观测值文件是以后缀名为.01O的格式保存。通过该观测文件读取相应的载波相位。由于存在卫星钟差,需要对数据进行时钟修正。打开cpy D0012361.01O文件进行读取,将读取的字符等赋值于fid。定义两个空数组D1Data 和idx,存放卫星编号以及载波相位数据,然后开始读取第一行数据。
卫星个数后面的‘G’用空格替换,并将第一行转换成数字存放在tmp中。判断第一行读取的数据是否为历元头,如果是历元头,那么定义一个29行1列的零矩阵sat ,再将sat存储在D1Data中,对应的行数即代表卫星的编号。
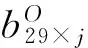
式中:1、2…29为卫星PRN编号,这是默认编号,程序中数据输出时并没有这些编号;φj,1~29为j历元的相应卫星号的载波相位观测值。加入某个历元只存在6、8、10、18、23、24、26号卫星,相应地,只存在φj,6,φj,8,φj,10,φj,18,φj,23,φj,24,φj,26,其余卫星的载波相位观测值为0。
同样按照上述处理过程,可以得到另外一个观测站的载波相位数据D2Data。经过这样的数据处理后,使得原先的数据结果变得简单,利于后面的差分计算[8]。
2.2 载波相位差分
在得到了D001NAV(两个站卫星星历是一样的,由于D001的星历卫星数比D002多,就只取用D001NAV数据即可)和D1Data 、D2Data数据后,就可以对数据进行时钟同步。通过revTime=0:20:((len-1)×20)将历元之间时间间隔分为20 s一次,使得D1,D2数据时钟同步,方便处理。
GPS差分算法的数据处理已经完成,接下来开始进入载波相位差分计算工作,包括各卫星的坐标及其载波相位计算、载波相位差分计算,得到基站与移动站之间的基线长度,从而实时观测基站和移动站之间的基线变化情况。
在一般外在条件下,GPS接收机可以观测的卫星数都大于4,GPS系统进行定位工作只需要4颗卫星就可以组成方程组进行解算,且这4颗卫星的相对几何位置对导航定位的精度影响很大,因此,需要从中选择最优卫星组合,这就产生了选星问题[9]。一般认为,要求卫星高度角大于10°,并且使得该卫星组合的几何精度因子最小,才能达到很好的定位精度。在此次仿真模拟中,通过计算选定了编号为6 、10、 23、 24的卫星。
图4为选定卫星的角度随历元之间时间间隔的变化,可以发现卫星6的角度初始只有2°左右,远没有达到选星的基本要求,由于计算模糊度是需要一定的时间的,当时间进行到第33个历元时,卫星6的角度大于10°,且其他卫星的角度都已超过10°,可以进行载波相位差分计算。
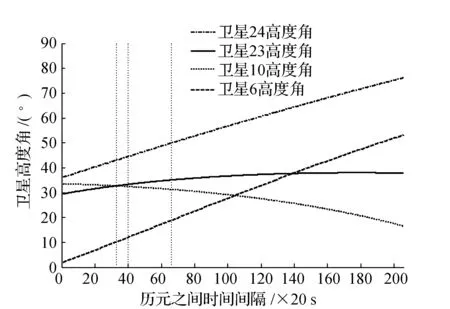
图4 卫星角度随历元之间时间间隔的变化
2.2.1 确定计算整周模糊度的历元时间间隔
由于载波相位差分算法的直接输出量为各卫星之间的整周模糊度差和移动站概略坐标以及差分后坐标的偏移向量[ΔxΔyΔz],通过基线参考值来验证算法,以下所有实验都基于上述4颗卫星。观察基线长度随历元时间间隔变化情况,结果如图5所示。
图5表明,两个历元间隔时间太短的情况下,解算出来的基线长度很不稳定。这主要由于较短时间的两个历元之间存在较大的相关性,不利于通过算法求解得到正确解。而当历元相隔660 s(33×20 s)或更长时间时,解算的基线长趋于稳定,且都在7 554~7 555 m之间。
这表明卫星角度的变化对载波相位差分的结果影响很大,在660 s之前,卫星6的高度角在10°以下,而后不断爬升,解算的结果趋向于稳定[10]。

图5 不同时间间隔历元间的载波相位差分
2.2.2 确定整周模糊度之后的差分坐标解算
由图5可知,计算载波相位差分整周模糊度时历元间要间隔足够长的距离。本仿真模拟测试为在整周模糊度确定后差分坐标解算的变换情况。整周模糊度计算的历元选择第一个历元和第40个历元,即历元间隔为40×20 s=800 s。然后可以根据算得的整周模糊度计算D002的差分坐标。仍然以基线长为参考值,结果如图6所示。
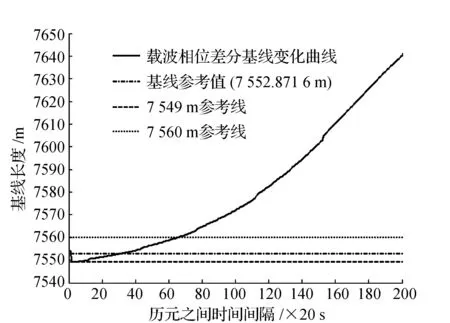
图6 确定模糊度之后的载波相位差分
在实际差分实验中,通过对图4中卫星角度的分析,图6中前800 s的基线解算结果是没有意义的,因为模糊度要到后面才计算出来。第800 s时的基线长与真值有1.2 m的误差,而在(66-40)×20 = 520 s的时间里,差分结果与真值之间可以控制在8 m之内。在此之后,差分定位的结果将持续向上漂移,导致误差越来越大。
当历元间隔在66×20 s以后,卫星24的高度角持续爬升到50°以上,那么根据卫星高度角的变化图,可以认为卫星角度的变化是造成最后定位结果不断向上漂移的原因。
3 结束语
本文主要论述了载波相位差分GPS算法及其数学模型、如何采用Matlab程序对载波相位差分算法中的数据进行处理并得出差分结果,这是GPS定位技术的主要部分。
采用Matlab进行仿真模拟,以图形的方式直观地表达载波相位差分计算过程,并进行相应的分析,评价计算载波相位差分整周模糊度的历元时间间隔并且在确定整周模糊度之后进行差分计算。实例证明,Matlab程序对于载波相位差分GPS算法中的数据处理是合理并且正确的。
[1] 刘基余.GPS卫星导航定位原理与方法[M].北京:科学出版社,2008.
[2] 焦海松, 李锋, 张松,等. 单基站差分 GPS 定位精度的分析与检验[J]. 全球定位系统, 2009, 34(1): 12-15.
[3] SPECHT C. Accuracy and coverage of the modernized Polish Maritime differential GPS system[J]. Advances in Space Research, 2011, 47(2): 221-228.
[4] 郭泉河, 王爱生. 载波相位的周跳对定位结果的影响分析[J]. 黑龙江工程学院学报:自然科学版, 2013, 27(3): 9-11.
[5] 崔卫磊, 唐斌, 李建飞, 等. 关于 GPS 基线解算以及质量控制的探讨[J]. 勘察科学技术, 2012 (4): 58-60.
[6] 张晋升,匡翠林,谢荣安,等. GPS自动变形监测软件设计与实现[J]. 工程勘察, 2013 (8): 67-70.
[7] 赵亚红,郝延锦,徐明侠. Matlab在测绘工程领域中的几点应用[J]. 地矿测绘,2011,27(1):38-40.
[8] 郭秋英,胡振琪. 差分GPS数据通信格式RTCM3.1及其解码算法的实现[J]. 测绘通报,2012(6):4-6.
[9] 吴瑞祥,蔡体菁. 基于高度角和方位角的选星方法[J]. 舰船电子工程,2009,29(11):73-75.
[10] ZHALILO A A, ZHELANOV A A, SHELKOVENKOV D A, et al. High-precision GPS-positioning using the phase observations of differential frequency[J]. Radioelectronics and Communications Systems, 2011, 54(2): 77-86.
[责任编辑:郝丽英]
Differential GPS algorithm analysis and software test based on Matlab
HUANG Jin1,SHI Xing-xi2
(1.China Railway Engineering Design Institute Co.Ltd., Jiangsu 226000, China; 2.School of Sciences,Nanjing University of Technology,Jiangsu 210094, China)
The correct analysis processing of the satellite data in the GPS positioning is the premise of differential GPS positioning work. This article discusses the differential GPS algorithm coupled with its observation model, and data processing method of the difference carrier phase algorithm based on the matlab program and than gets the final simulation results. The results indicate that the data processing method is correct and effective.
differential GPS;observation model; observation model; data processing;Matlab program
2014-11-09
黄 金(1988-),男,助理工程师,研究方向:GPS定位及其在滑坡监测中的应用.
P228.4
A
1671-4679(2015)02-0030-05

