基于Copula-Monte Carlo法的水库下游洪水概率分布研究

刘章君，郭生练，胡 瑶，杨 光，尹家波

(武汉大学水资源与水电工程科学国家重点实验室，湖北武汉430072)

基于Copula-Monte Carlo法的水库下游洪水概率分布研究

刘章君，郭生练，胡 瑶，杨 光，尹家波

(武汉大学水资源与水电工程科学国家重点实验室，湖北武汉430072)

利用Copula函数构造水库调洪控制时段洪量和区间洪峰的联合分布，通过调洪函数将水库入库洪量转换为下泄洪峰，随机模拟得到两分区洪峰流量，提出了推求水库下游洪水概率分布的Copula-Monte Carlo(Copula-MC)方法。应用清江流域隔河岩水库实例进行验证，推求下游高坝洲断面的洪水概率分布，并与忽略洪水相关性的独立MC法进行比较，结果表明，独立MC法计算的洪峰流量系统偏小，会低估高坝洲断面的防洪风险；Copula-MC法得到的100年一遇高坝洲断面设计洪水与天然情况下相比减小32.6%。Copula-MC法充分考虑了上游水库断面和区间洪水的空间相关性及地区组成的随机性，结果合理可行。

水库调蓄；概率分布；Copula函数；Copula-Monte Carlo法；清江流域

0 引 言

设计断面的洪水概率分布是对其洪水情势的统计描述，是各类水利水电工程规划设计中的重要依据。河流上游调蓄作用较大的水库对洪水具有调节作用，改变了下游天然洪水的时程分配及峰、量，从而影响下游洪水的概率分布。研究上游水库如何进行设计才能满足下游设计断面的防洪要求，或者当水库的泄洪设施规模、防洪库容等参数确定时，水库对下游设计断面的影响等问题，都需要研究受水库调洪影响后下游洪水的概率分布问题[1- 2]。

目前的计算方法可以分为“自下而上”和“自上而下”两大类。前者通过拟定设计断面设计洪水的地区组成，即将设计断面设计洪量分配给上游各分区以研究水库的调洪影响。选择科学合理的分配规则来分配设计洪量是此类方法的关键。由于各分区洪水有一定的相关性，其相互遭遇组合具有明显的随机性，给实际分析带来了很大的困难。学者们先后提出了典型年法和同频率地区组成法两种常用方法[1- 2]及最近的JC法[3- 4]和Copula函数法[5- 7]等洪量分配规则。然而，这类方法简单地假定水库调蓄后设计断面的洪水与天然情况同频率，没有充分考虑洪水地区组成的随机特性和水库的调洪影响。后者则较好地克服了上述问题，它不去研究如何分配设计断面的设计洪量，而是研究上游各分区洪水所有可能的组合遭遇情况，能够反映水库对不同频率洪水的调洪效应。该类方法按照处理方式的不同主要包括概率组合离散求和法和随机模拟法[1- 2]。由于上游水库断面和区间洪水通常具有空间相关性，使得离散求和法往往受到联合概率分布函数求解的限制，需要对变量进行独立性处理，难免出现信息失真，具有较大的局限性。为此，文献[8]通过Copula函数直接对条件概率曲线进行离散，克服了离散求和法需要进行变量独立性转换的问题，提出了改进的离散求和法。随机模拟法利用随机模拟技术建立设计断面及各分区洪水过程线的模拟模型，用人工方法随机生成足够长的、能满足设计需要的洪水资料系列，通过长系列洪水资料直接求出设计断面受水库调洪影响后的洪水频率曲线及设计值。该法的精度主要取决于所建立的随机模型是否合理，能否反映洪水的客观规律[9]。

本文结合随机模拟法思想，考虑上游水库调洪控制时段洪量和区间洪峰间的相关性，利用Copula函数构造其联合分布；通过水库调洪函数将水库入库洪量转换为最大下泄流量，随机模拟得到两分区洪峰流量；提出推求水库下游洪水概率分布的Copula-Monte Carlo(Copula-MC)方法。以清江流域隔河岩水库为例对所提方法进行验证，并探讨是否考虑分区洪水空间相关性对计算结果的影响。

1 问题的数学描述

典型单库防洪系统中A为上游水库，C为设计断面，B为水库与设计断面之间的区间流域。X、Y及QA分别为水库A来水、区间B来水和经水库A调蓄后的下泄洪水，显然它们均可被视为随机变量，概率分布函数分别用FX(x)、FY(y)及FQA(qA)表示。由于对调洪能力较大的水库洪量往往其控制作用，因此令X表示洪量，Y与QA表示流量。QA由水库来水X和水库调洪函数gA(·)所确定(见图1)

QA=gA(X)

(1)

图1 单库防洪系统示意

断面C处受水库调洪影响后的洪水流量Z也是一随机变量，并且等于水库的下泄洪水QA与区间来水Y之和(考虑洪水传播时间)，即

Z=QA+Y

(2)

现欲推求Z的概率分布FZ(z)。它可由QA和Y的联合分布来确定，即联合概率密度fQA,Y(qA,y)通过以下积分确定[2]。即

(3)

式中，qA0、y0分别为QA和Y的样本空间的下界。

式(3)从理论上给出了FZ(z)的计算方法，但实际中往往因水库最大下泄流量QA的概率分布非常复杂，常需分段处理；且QA、Y的空间相关性使得QA和Y的联合分布难以求解。因此，本文拟采用Copula-MC法避开QA和Y联合分布求解的难题，首先构造X和Y的联合分布，再联合抽样模拟大量样本(x，y)，通过水库调洪函数qA=gA(x)得到(qA，y)，qA与y相加后统计得到设计断面洪峰的概率分布曲线及设计值。

2 水库调洪函数

在推求设计断面洪水概率分布函数时，通常认为水库本身的泄洪设施及调洪规则已经确定，假定水库的泄量仅与来水有关[2]。对于调洪库容较大的水库，调洪结果主要受入库洪水总量控制。假定来水x出现大小不同的洪量w1、w2…，选择一个典型洪水过程线，按洪量控制放大过程线，并经水库调洪演算，得到对应于wi的最大下泄流量qAi，点绘wi-qAi相关图。如果水库采用自由泄流方式，可根据点群中心采用一个曲线函数进行拟合求得该函数表达式qA=gA(x)。如果水库有控泄要求，在某些洪量范围内，下泄量qA成一水平直线，有时在某一洪量上下，下泄量发生突变。此时，可将洪量进行分段，对每一段采用不同的函数表达式拟合，将函数表达式组成函数组作为水库的调洪函数一般可表示为[2，10]

(4)

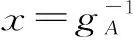
(5)

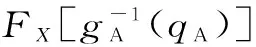
3 Copula-Monte Carlo方法

3.1 Copula函数

Copula函数是定义域为[0，1]均匀分布的多维联合分布函数，根据Sklar定理，它可以将多个随机变量的边缘分布连接起来构造联合分布。一般而言，水库断面和区间流域洪水之间存在较强的正相关性，通常采用Gumbel-Hougaard Copula函数来构造二者的联合分布[11- 13]，数学表达式为

(6)

式中，u=FX(x)和v=FY(y)分别代表边缘分布函数，Copula函数参数θ与Kendall秩相关系数τ的关系为θ=1/(1-τ)[14]。

3.2 推求水库下游洪水概率分布的基本步骤

通过联合分布函数可以对存在相关性的随机变量X和Y成对地进行随机抽样，从而达到对二者同时随机模拟的目的，进而给出计算水库下游洪水概率分布的Copula-MC法。具体步骤如下[15]：

(1)根据建立的两变量联合分布，可以得到当X为指定值x时Y的条件分布，数学表达式为

(7)

(2)产生服从[0，1]均匀分布的两个独立随机数r1和r2。

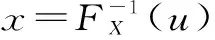
(4)令r2等于X=x时Y的条件分布值，即r2=SX(y|X=x)，式(7)计算繁琐，为求解方便，将式(7)表达为

(8)

(5)通过z=qA+y计算得到z。

(6)重复步骤 2～5共n次，可以模拟出n个z值，采用数学期望公式[1]计算经验频率，得到水库下游设计断面的洪水概率分布。

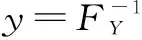
4 应用实例

清江是湖北省境内最大的一条长江支流，发源于湖北省利川市齐岳山，流域面积1.7万km2(见图1)，实例中A为隔河岩水库，C为高坝洲断面，B为隔河岩-高坝洲区间流域(简称“隔-高区间”)。隔河岩水库控制面积14 430 km2，具有年调节能力；高坝洲水库位于隔河岩水库下游50 km处，控制面积15 650 km2，为径流式电站，无调节能力；隔-高区间面1 220 km2，在此区间洪水传播时间较短，可不考虑河道调蓄作用。隔河岩水库为长江错峰预留5.0亿m3防洪库容，必然会改变高坝洲断面天然洪水的概率分布。

4.1 边缘分布

按照我国《水利水电工程设计洪水计算规范》[1]的规定，假设隔河岩水库断面最大3 d洪量和隔-高区间、高坝洲断面天然洪峰流量均服从P-Ⅲ分布，各水库断面和区间的天然设计洪水统计参数见表1。采用χ2检验法进行假设检验，在5%的显著性水平下，自由度为k-r-1(r为参数个数，k为χ2检验的分组数)的χ2检验的接受域为小于等于临界值，表中χ0.05为临界值，3个随机变量的P-III型分布均通过了检验。

表1 各分区天然设计洪水统计参数

4.2 隔河岩水库调洪函数

根据隔河岩水库对洪水的调节特性，选取3d为控制时段。经计算，隔河岩断面最大3d洪量2年一遇的值为9.82亿m3，1 000年一遇的值为39.35亿m3。在推求水库调洪函数时，假定入库洪量取值从8亿～42亿m3，离散间距0.05亿m3，以离散的3 d洪量为控制，按1997年典型洪水过程线同倍比放大得到各自的设计洪水过程线，输入到隔河岩水库按调洪规则[9]进行调洪演算得到该洪量对应的最大下泄流量，点绘曲线(x，qA)(见图2)。

某桥梁位于太原市某主干路上，为1座南北走向的5跨简支普通钢筋混凝土实心板梁桥，跨径组合为5×6.7 m，桥梁中心线与河道中心线法线逆交10°，桥面总宽35 m。每跨上部结构均由33榀普通钢筋混凝土实心板梁组成，人行道下实心板梁与车行道下实心板梁间无铰缝连接，梁高均为0.33 m，每跨8号、9号、22号、23号实心板梁底宽均为1.5 m，其余板梁底宽均为1.0 m，桥面铺装为约20 cm厚的沥青混凝土。该桥曾进行拓宽改建，改建时仅保留了老桥的下部结构，并于其两侧各新建了一幅桥。该桥梁的横断面示意图见图1。

对调洪函数进行分段拟合，得

(9)

图2 隔河岩水库调洪函数

对式(9)所得函数进行检验，将所有离散点据对应的洪量采用调洪函数进行计算得到对应的最大下泄流量，与实际调度值进行比较，发现相对误差均不超过2%，表明简化得到的调洪函数精度较高，能满足计算要求。可由式(9)及隔河岩水库天然来水最大3 d洪量的概率分布求得隔河岩水库最大下泄流量的概率分布，如式(10)和图3所示。

(10)

图3 隔河岩水库下泄洪峰的概率分布曲线

可以看出，根据入库洪水量级的大小，可以将隔河岩水库下泄洪峰的概率分布分为5个阶段： I当入库洪量<16.70亿m3时，水库按来多少水泄多少水的方式运行；II当入库洪量>16.70亿m3时，为满足下游防洪要求水库按一级控泄流量11 000 m3/s进行控泄；III当入库洪量>33.15亿m3时，为满足下游防洪要求水库按二级控泄流量13 000 m3/s进行控泄；IV当入库洪量>37.09亿m3时，表明该次洪水的量级已超过下游防洪标准，水库不再承担下游防洪任务，水库敞泄运行；V当入库洪量>38.35亿m3时，表明该次洪水的量级已超过设计标准，同时临时性启用非常泄洪措施进行敞泄，以确保水库的安全。阶段I随着入库洪水量级的增大而逐步转换到阶段V。4次转换过程中，只有阶段I到阶段II的转换过程是渐变形成的，其他3次均为突变。3个突变点的设计频率分别为0.41%、0.17%和0.125%。这造成最大下泄流量在区间(11 000， 13 000)、(13 000， 15 495) 、(16 038， 20 715) m3/s出现“空缺”。另外，在阶段II和阶段III由于水库采用控泄的调洪方式，设计频率[0.41%， 13.98%]对应的最大下泄流量均为11 000 m3/s；设计频率[0.17%， 0.41%]对应的最大下泄流量均为13 000 m3/s。

“自下而上”类方法通常将下游设计断面设计洪量分配给上游各分区以研究水库的调洪影响。这类方法对洪量的分配方案具有很强的依赖性，科学合理的分配规则极为重要，当上游水库具有复杂调洪规则(如有控泄要求)时，这类方法的可靠性较差，科学合理性将受到质疑[16]。本文所提Copula-MC法则不需要研究如何分配高坝洲断面的设计洪量，可以考虑隔河岩断面和隔-高区间洪水所有可能的组合遭遇情况，较好地反映洪水地区组成的随机特性和水库的调洪影响。

4.3 两分区洪峰流量随机生成

采用1958年～2010年隔河岩断面最大3 d洪量和区间洪峰资料，得到秩相关系数为0.674，联合分布的参数为3.07。通过联合分布的经验频率和理论频率，计算了实测样本的均方根误差(RMSE)[17]，结果为0.030 7，说明Gumbel-Hougaard Copula函数对联合分布的拟合效果较好。将53年的经验联合分布值与理论联合分布值点绘为图4，其确定性系数为0.991 9，经验频率与理论频率值的拟合情况很好。图5是另外一种形式对联合观测变量的经验联合分布值与理论联合分布值进行的对比。图4和图5表明所建立的联合分布是合理可行的。

图4 经验频率和理论频率相关关系

图5 经验频率和理论频率比较

运用上述3.2节中的Copula-MC法和独立MC法，各模拟1万组隔河岩水库最大3d洪量及隔-高区间洪峰，结果点绘于图6。对比图6a和图6b可知，考虑两分区洪水的相关性情况下，随机模拟的散点分布较为集中且散点在某一直线附近聚集，而未考虑时，散点均匀的散布在整个二维空间区域。这说明两种方法模拟的隔河岩水库最大3d洪量及隔-高区间洪峰组合差异较大。将实测资料点据点绘在随机模拟的散点图中，可以看出Copula-MC法由于考虑了洪水相关性，对实测资料的吻合效果更好，构建的随机模型更能反映实际情况。

图6 隔河岩断面最大3 d洪量与隔-高区间洪峰随机生成散点

4.4 受隔河岩水库影响的高坝洲断面洪水概率分布

利用上述随机生成的大量高坝洲断面洪峰流量，采用数学期望公式计算经验频率，得到Copula-MC法和独立MC法计算得到的受隔河岩水库影响的高坝洲断面洪峰流量频率曲线(见图7)；同时，将天然情况下的高坝洲断面洪峰流量频率曲线也列于图7，以便分析隔河岩水库的调洪作用对高坝洲断面洪峰流量频率曲线的影响。将6种常用设计频率的计算结果列于表2。

图7 三种情形下高坝洲断面洪峰流量频率曲线

从图7和表2的计算结果可以发现：与高坝洲断面天然洪峰流量相比，两种方法计算的受隔河岩水库调蓄影响的洪峰流量均有不同程度的削减。可以发现，隔河岩水库对于中小洪水的调节作用不显著，故受其调洪影响的高坝洲断面洪峰流量频率曲线与天然情况无明显差异；对于大洪水过程则调节能力逐渐减弱，整体规律与实际情况相符。与Copula-MC法相比，独立MC法推求的高坝洲断面洪峰流量系统偏小，最大可达10%左右。因此，不考虑两分区洪水的空间相关性会低估高坝洲断面的防洪风险。Copula-MC法计算的高坝洲断面100年一遇洪峰流量由天然情况的18 800 m3/s减小为12 670 m3/s(此值相当于高坝洲断面天然情况下10年一遇设计洪水)，削减6 130 m3/s(32.6%)。由此可知，隔河岩水库的调洪作用对高坝洲断面设计洪水的影响巨大。

表2 高坝洲断面设计洪峰流量计算结果对比

5 结 论

应用清江流域隔河岩水库实例对本文提出的方法进行验证，主要研究结论如下：

(1)所提方法能充分考虑上游水库断面和区间洪水的空间相关性及地区组成的随机性，结果合理可行。受隔河岩水库调洪的影响，高坝洲断面天然洪峰流量均有不同程度的削减，Copula-Monte Carlo方法推求的100年一遇设计洪水的削峰率达到32.6%。

(2)独立Monte Carlo法假定各分区洪水相互独立，忽略了洪水的空间相关性，计算的洪峰流量与Copula-Monte Carlo法相比系统偏小，会低估设计断面的防洪风险。

[1] SL44—2006 水利水电工程设计洪水计算规范[S].

[2] 水利部长江水利委员会水文局， 水利部南京水文水资源研究所. 水利水电工程设计洪水计算手册[M]. 北京： 中国水利水电出版社， 2001．

[3]谢小平， 黄灵芝， 席秋义， 等. 基于JC法的设计洪水地区组成研究[J]. 水力发电学报， 2006， 25(6)： 125- 129．

[4]黄灵芝， 谢小平， 黄强， 等. 梯级水库设计洪水地区组成研究中的JC法[J]. 自然灾害学报， 2006， 15(4)： 163- 167．

[5]闫宝伟， 郭生练， 郭靖， 等. 基于Copula函数的设计洪水地区组成研究[J]. 水力发电学报， 2010， 29(6)： 60- 65．

[6]刘章君， 郭生练， 李天元， 等. 基于Copula函数的梯级水库设计洪水地区组成研究[J]. 水资源研究， 2014， 3(2)： 124- 135．

[7]刘章君， 郭生练， 李天元， 等. 梯级水库设计洪水最可能地区组成法计算通式[J]. 水科学进展， 2014， 25(4)： 549- 558．

[8]李天元， 郭生练， 刘章君， 等. 梯级水库下游设计洪水计算方法研究[J]. 水利学报， 2014， 45(6)： 641- 648．

[9]李雨， 郭生练， 周研来， 等. 考虑入库洪水随机过程的梯级水库防洪优化调度[J]. 四川大学学报： 工程科学版， 2012， 44(6)： 13- 20．

[10]何长宽. 用概率组合法确定并联水库下游洪峰流量的概率分布[J]. 水利水电技术， 1998， 29(7)： 49- 51．

[11]张娜， 郭生练， 肖义， 等. 基于联合分布的设计暴雨方法[J]. 水力发电， 2008， 34(1)： 18- 21．

[12]杨立峰， 周研来， 夏世明， 等. 基于阿基米德联合函数的洪水过程随机模拟研究[J]. 水力发电， 2011， 37(4)： 20- 23．

[13]冯平， 李新. 基于 Copula 函数的非一致性洪水峰量联合分析[J]. 水利学报， 2013， 44(10)： 1137- 1147．

[14]刘和昌， 梁忠民， 姚轶， 等. 基于 Copula 函数的水文变量条件组合分析[J]. 水力发电， 2014， 40(5)： 13- 16．

[15]肖义， 郭生练， 熊立华， 等. 一种新的洪水过程随机模拟方法研究[J]. 四川大学学报： 工程科学版， 2007， 39(2)： 55- 60．

[16]王锐琛， 陈源泽， 孙汉贤. 梯级水库下游洪水概率分布的计算方法[J]. 水文， 1990， 9(1)： 1- 8．

[17]郭生练， 闫宝伟， 肖义， 等. Copula函数在多变量水文分析计算中的应用及研究进展[J]. 水文， 2008， 28(3)： 1- 7．

(责任编辑 陈 萍)

Flood Probability Distribution Estimation under the Influence of Upstream Reservoir Regulation Based on Monte Carlo Method

LIU Zhangjun， GUO Shenglian， HU Yao， YANG Guang， YING Jiabo

(State Key Laboratory of Water Resources and Hydropower Engineering Science，Wuhan University， Wuhan 430072， Hubei， China)

The joint distribution of controlling flood volume at reservoir site and peak discharge at interval basin is firstly constructed based on Copula function， then the reservoir inflowing flood volume is transformed into outflow peak discharge by using flood regulation function and the flood peak discharge at the two sub-basins is got by using stochastic simulation method， and finally the Copula-Monte Carlo (Copula-MC) method for flood probability distribution estimation is developed. The Qingjiang basin is chosen as the case study and the peak discharge probability distribution of Gaobazhou site is estimated under the influence of Geheyan Reservoir by using Copula-MC method， and the results are compared with Independence-MC method that ignores the correlation. The results demonstrate that the flood peaks of Independence-MC method are systematically smaller than those of Copula-MC method， which may lead to an increased risk in Gaobazhou site， and the 100-year design peak discharge estimated by Copula-MC method at Gaobazhou site has been cut by 32.6%. The calculation results of proposed Copula-MC method are reasonable because it can capture the spatial correlation of floods occurred at each sub-basin and reflects the stochastic characteristics of flood region composition．

reservoir regulation; probability distribution; Copula function; Copula-Monte Carlo method; Qingjiang Basin

2014- 12- 12

国家自然科学基金重大项目(51190094)

刘章君(1991—)，男，江西吉安人，博士研究生，研究方向为水文分析与计算.

TV122.3

A

0559- 9342(2015)08- 0017- 06